Содержание

Исходные данные. 3

1.   Корреляционный анализ. 4

1.1. Построить матрицу парных коэффициентов корреляции. 4

1.2. Проверить значимость парных коэффициентов корреляции. (Уровень значимости выбирается самостоятельно) 5

1.3. Для любого значимого коэффициента построить доверительный интервал. 6

1.4.    Рассчитать множественный коэффициент корреляции. Проверить его значимость. 6

2.   Регрессионный анализ. 8

2.1.    Получить оценку предложенной множественной регрессионной модели, используя методы матричной алгебры. 8

2.2.    Проверить значимость каждого коэффициента регрессии. 9

2.3. Определить доверительный интервал для значимых коэффициентов регрессии. 10

3.   Дисперсионный анализ. 11

3.1. Получить оценку коэффициента детерминации. 11

Коэффициент детерминации находим по формуле: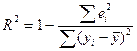.......................... 11

3.2.    Проверить его значимость. 11

4. Проверка модели на присутствие гетероскедастичности и автокорреляции. 11

4.1.    Используя тест Дарбина – Уотсона, проверить модель на наличие автокорреляции в «остатках». 11

4.2. Используя тест ранговой корреляции Спирмена или тест Голдфелда – Квандта, проверить полученную модель на присутствие гетероскедастичности. 13

Список литературы.. 15


Исходные данные


Имеются данные о прибыли, производительности труда и рентабельности предприятия за 1985 – 2000 год.

Годы

Прибыль

( млрд. р.)

Производительность

труда

( тонны/час )

Рентабельность

(y %)

1985

4,8

3

2

1986

3,5

2,9

1,8

1987

3,1

2,8

1,8

1988

3,3

2,7

1,9

1989

3,5

2,8

2,1

1990

3,7

3

2,2

1991

3,8

3,3

2,5

1992

4,2

3,6

2,4

1993

4,6

3,9

2,6

1994

4,7

4,1

2,8

1995

5,1

3,8

2,7

1996

4,7

3,7

2,2

1997

4,8

4,2

2,8

1998

5

4,1

3,1

1999

5

4,1

2,9

2000

4,9

4,3

2,8

1.    Корреляционный анализ


1.1. Построить матрицу парных коэффициентов корреляции.

Решение.

Коэффициент парной корреляции находится по формуле:

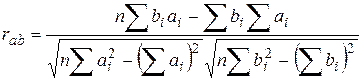
Для расчета коэффициента корреляции используем таблицу:




1

4,8

3

23,04

9

14,4

2

3,5

2,9

12,25

8,41

10,15

3

3,1

2,8

9,61

7,84

8,68

4

3,3

2,7

10,89

7,29

8,91

5

3,5

2,8

12,25

7,84

9,8

6

3,7

3

13,69

9

11,1

7

3,8

3,3

14,44

10,89

12,54

8

4,2

3,6

17,64

12,96

15,12

9

4,6

3,9

21,16

15,21

17,94

10

4,7

4,1

22,09

16,81

19,27

11

5,1

3,8

26,01

14,44

19,38

12

4,7

3,7

22,09

13,69

17,39

13

4,8

4,2

23,04

17,64

20,16

14

5

4,1

25

16,81

20,5

15

5

4,1

25

16,81

20,5

16

4,9

4,3

24,01

18,49

21,07

сумма

68,7

56,3

302,21

203,13

246,91

Получаем:

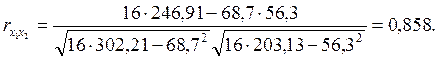
Аналогично считаются парные коэффициенты корреляции и.

Можно найти матрицу парных коэффициентов корреляции используя средства редактора EXCEL:

 

Столбец 1

Столбец 2

Столбец 3

Столбец 1

1

0,85814

0,79195

Столбец 2

0,85814

1

0,918495

Столбец 3

0,79195

0,918495

1

1.2. Проверить значимость парных коэффициентов корреляции. (Уровень значимости выбирается самостоятельно)

Решение.

Проверяем значимость коэффициента корреляции 0,792 при уровне значимости . Так как

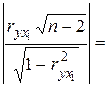4,85 >1,761, то  существенно отличается от 0, значим и существует сильная линейная положительная связь между y и .


Аналогично проверим неравенство для  0,918:

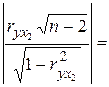8,69>1,761, значит, также существенно отличается от 0, значим и существует сильная линейная положительная связь между y и. .


 Для 0,858:

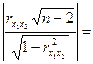6,25>1,761, значит,  существенно отличается от 0, значим и существует сильная линейная положительная связь между и .


1.3. Для любого значимого коэффициента построить доверительный интервал.

Решение.



1.1  Рассчитать частный коэффициент корреляции (любой). Проверить его значимость.

Решение. Частный кэффициент корреляции находим по формуле:

 

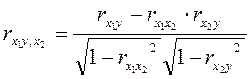
Получаем

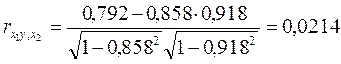
1.4.         Рассчитать множественный коэффициент корреляции. Проверить его значимость.

Решение.

Для нахождения уравнения регрессии  используем средства редактора EXCEL:

ВЫВОД ИТОГОВ







Регрессионная статистика


Множественный R

0,918524


R-квадрат

0,843686


Нормированный R-квадрат

0,819638


Стандартная ошибка

0,178757


Наблюдения

16







Дисперсионный анализ

 

df

SS

MS

F

Регрессия

2

2,242096

1,121048

35,08298

Остаток

13

0,415404

0,031954

Итого

15

2,6575

 

 





 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Y-пересечение

0,056192

0,297166

0,189094

0,85294

Переменная X 1

0,008643

0,129491

0,066747

0,947799

Переменная X 2

0,659097

0,155328

4,243261

0,000959

Таким образом,  

Коэффициент R множественной корреляции определяется по формуле:

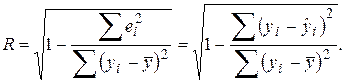
Воспользуемся вспомогательной таблицей:


i

1

2,0750

-0,4125

-0,0750

2

1,9978

-0,6125

-0,1978

3

1,9285

-0,6125

-0,1285

4

1,8643

-0,5125

0,0357

5

1,9319

-0,3125

0,1681

6

2,0655

-0,2125

0,1345

7

2,2641

0,0875

0,2359

8

2,4652

-0,0125

-0,0652

9

2,6664

0,1875

-0,0664

10

2,7991

0,3875

0,0009

11

2,6048

0,2875

0,0952

12

2,5355

-0,2125

-0,3355

13

2,8659

0,3875

-0,0659

14

2,8017

0,6875

0,2983

15

2,8017

0,4875

0,0983

16

2,9327

0,3875

-0,1327

Сумма квадратов

2,4873

0,4098

Тогда R=0,9185.

Так как

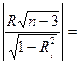8,375 >1,771, то R существенно отличается от 0 и существует сильная связь между y и , .

Вывод по разделу 1.

Проведенные исследования показали, что между переменными существует сильная связь. Так как парные коэффициенты корреляции положительны, то с ростом прибыли и производительности труда происходит рост  рентабельности.


2.      Регрессионный анализ.


2.1.         Получить оценку предложенной множественной регрессионной модели, используя методы матричной алгебры.

Решение.

Уравнение регрессии ищем в виде:

.

Обозначения

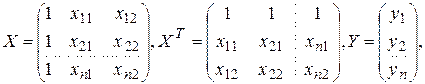
тогда

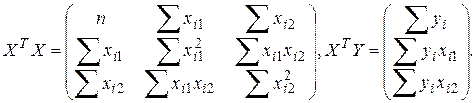
Вектор  находится по формуле:

Используем таблицу:

y






1

4,8

3

2

23,04

9

9,6

6

14,4

4

2

3,5

2,9

1,8

12,25

8,41

6,3

5,22

10,15

3,24

3

3,1

2,8

1,8

9,61

7,84

5,58

5,04

8,68

3,24

4

3,3

2,7

1,9

10,89

7,29

6,27

5,13

8,91

3,61

5

3,5

2,8

2,1

12,25

7,84

7,35

5,88

9,8

4,41

6

3,7

3

2,2

13,69

9

8,14

6,6

11,1

4,84

7

3,8

3,3

2,5

14,44

10,89

9,5

8,25

12,54

6,25

8

4,2

3,6

2,4

17,64

12,96

10,08

8,64

15,12

5,76

9

4,6

3,9

2,6

21,16

15,21

11,96

10,14

17,94

6,76

10

4,7

4,1

2,8

22,09

16,81

13,16

11,48

19,27

7,84

11

5,1

3,8

2,7

26,01

14,44

13,77

10,26

19,38

7,29

12

4,7

3,7

2,2

22,09

13,69

10,34

8,14

17,39

4,84

13

4,8

4,2

2,8

23,04

17,64

13,44

11,76

20,16

7,84

14

5

4,1

3,1

25

16,81

15,5

12,71

20,5

9,61

15

5

4,1

2,9

25

16,81

14,5

11,89

20,5

8,41

16

4,9

4,3

2,8

24,01

18,49

13,72

12,04

21,07

7,84

сумма

68,7

56,3

38,6

302,21

203,13

169,21

139,18

246,91

95,78

Получаем:

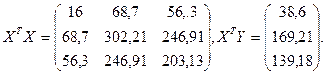
Тогда .

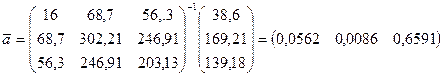Таким образом,


2.2.         Проверить значимость каждого коэффициента регрессии.

Решение.

Для проверить значимости  коэффициента регрессии bj проверяем выполнение неравенства  , где , .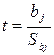


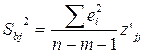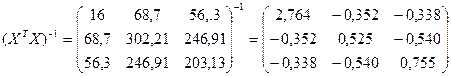
Для b0=0,0562:

  , .

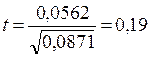Так как , то коэффициент b0=0,0562 не является значимым.


Для b1=0,0086:

  , .

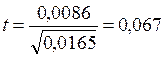Так как , то коэффициент b1=0,0086 не является значимым.


Для b2=0,6591:

  , .

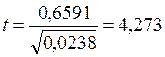Так как , то коэффициент b2=0,6591 является значимым.

 

2.3. Определить доверительный интервал для значимых коэффициентов регрессии.

Решение.

Строим доверительный интервал для коэффициента b2=0,6591.

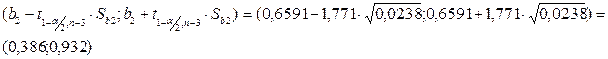
Вывод по разделу 2.

Зависимость рентабельности от прибыли и производительности труда описывается уравнением

Значимым  в этом уравнении является только коэффициент при х2 , который с вероятностью 0,9 принадлежит интервалу (0,386; 0,932).

3.      Дисперсионный анализ


3.1. Получить оценку коэффициента детерминации.

Решение.

Коэффициент детерминации находим по формуле: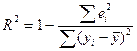

Получаем .


3.2.         Проверить его значимость.

Решение. Для проверки значимости коэффициента детерминации используем F-статистику:

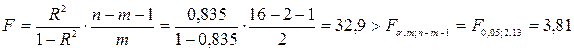
Следовательно, коэффициент детерминации статистически значим.


Вывод по разделу 3.

Близость к 1 и значимость коэффициента детерминации говорят о том, что  полученное уравнения множественной регрессии достаточно точно отражает зависимость рентабельности от прибыли и производительности труда.


4. Проверка модели на присутствие гетероскедастичности и автокорреляции


4.1.         Используя тест Дарбина – Уотсона, проверить модель на наличие автокорреляции в «остатках».

Решение.

Критерий Дарбина-Уотсона имеет вид:

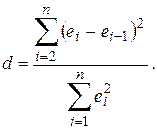
где - отклонения от линии регрессии, i=1,..n.

Для регрессионной модели :

Используя таблицу:

1

-0,0750

2

-0,1978

-0,1229

3

-0,1285

0,06937

4

0,0357

0,16418

5

0,1681

0,13236

6

0,1345

-0,0335

7

0,2359

0,10141

8

-0,0652

-0,3012

9

-0,0664

-0,0012

10

0,0009

0,06732

11

0,0952

0,09427

12

-0,3355

-0,4306

13

-0,0659

0,26959

14

0,2983

0,36418

15

0,0983

-0,2

16

-0,1327

-0,231

сумм кв

0,4098

0,66401

Посчитаем d=1,6204.

У нас n=16, m=2, , следовательно, условие 0,98=>d>=1,54 не выполняется, значит, автокорреляция присутствует.   


4.2. Используя тест ранговой корреляции Спирмена или тест Голдфелда – Квандта, проверить полученную модель на присутствие гетероскедастичности.

Решение.

Проверим полученную модель на присутствие гетероскедастичности для каждой переменной, используя тест ранговой корреляции Спирмена.

Ранжируем значения х1i  и ei и найдем коэффициент ранговой корреляции.

i

х1i

Ранг  х1i

ei

Ранг ei

di

di2

1

4,8

11

-0,075

5

6

36

2

3,5

3

-0,1978

2

1

1

3

3,1

1

-0,1285

4

-3

9

4

3,3

2

0,0357

10

-8

64

5

3,5

4

0,1681

14

-10

100

6

3,7

5

0,1345

13

-8

64

7

3,8

6

0,2359

15

-9

81

8

4,2

7

-0,0652

8

-1

1

9

4,6

8

-0,0664

6

2

4

10

4,7

9

0,0009

9

0

0

11

5,1

16

0,0952

11

5

25

12

4,7

10

-0,3355

1

9

81

13

4,8

12

-0,0659

7

5

25

14

5

14

0,2983

16

-2

4

15

5

15

0,0983

12

3

9

16

4,9

13

-0,1327

3

10

100

сумма




604

Коэффициент ранговой корреляции:

.

Так как 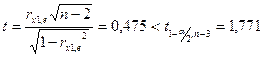, то гетероскедастичность для переменной х1 отсутствует.


Ранжируем значения х2i  и ei и найдем коэффициент ранговой корреляции.

i

х1i

Ранг  х1i

ei

Ранг ei

di

di2

1

3

5

-0,075

5

0

0

2

2,9

4

-0,1978

2

2

4

3

2,8

2

-0,1285

4

-2

4

4

2,7

1

0,0357

10

-9

81

5

2,8

3

0,1681

14

-11

121

6

3

6

0,1345

13

-7

49

7

3,3

7

0,2359

15

-8

64

8

3,6

8

-0,0652

8

0

0

9

3,9

11

-0,0664

6

5

25

10

4,1

12

0,0009

9

3

9

11

3,8

10

0,0952

11

-1

1

12

3,7

9

-0,3355

1

8

64

13

4,2

15

-0,0659

7

8

64

14

4,1

13

0,2983

16

-3

9

15

4,1

14

0,0983

12

2

4

16

4,3

16

-0,1327

3

13

169

сумма




668

Коэффициент ранговой корреляции:

.

Так как 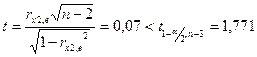, то гетероскедастичность для переменной х2   отсутствует.

Вывод по разделу 4.

Присутствие автокорреляции говорит о том, что выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Однако отсутствие гетероскедастичности дает надежду на правильность полученных заключений.




Список литературы


1. Теория статистики: Учебник/ Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 1996. – 464 с.

2. Социальная статистика: Учебник/ Под ред. чл.-кор. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 480 с.

3.  Сидоренко Е.В. Методы математической обработки в психологии. - СПб.: СПбГУ, 2000. – 367 с.

4. Общая теория статистики: Учебник/ под ред. чл.-корр. РАН И.И. Елисеевой. – М.: Финансы и статистика, 1999. – 484 с.

5. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник/ под ред. О.Э. Башиной, А.А. Спирина.- М.: Финансы и статистика, 1999. – 440 с.