Постановка задачи

При проведении статистического наблюдения за деятельностью предприятий корпорации получены выборочные данные по 32-м предприятиям, выпускающим однородную продукцию  (выборка 10%-ная, механическая), о среднегодовой стоимости основных производственных фондов и  о выпуске продукции за год.

В проводимом статистическом исследовании обследованные предприятия выступают как единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.

Для проведения автоматизированного статистического анализа совокупности выборочные данные представлены в формате электронных таблиц процессора Excel в диапазоне ячеек B4:C35. Для демонстрационного примера (ДП) выборочные данные приведены в табл. 1-ДП.

Таблица 1-ДП

Исходные данные демонстрационного примера

В процессе исследования совокупности необходимо решить ряд статистических задач для выборочной и генеральной совокупностей.

Статистический анализ выборочной совокупности

1.    Выявить наличие среди исходных данных резко выделяющихся значений признаков («выбросов» данных) с целью исключения из выборки аномальных единиц наблюдения.

2.    Рассчитать обобщающие статистические показатели совокупности по изучаемым признакам: среднюю арифметическую (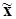), моду (Мо), медиану (Ме), размах вариации (R), дисперсию(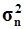), средние отклонения – линейное (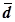) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии  К.Пирсона (Asп).

3.    На основе рассчитанных показателей в предположении, что распределения единиц по обоим признакам близки к нормальному, оценить:

а) степень колеблемости значений признаков в совокупности;

б) степень однородности совокупности по изучаемым признакам;

в) устойчивость индивидуальных значений признаков;

г) количество попаданий индивидуальных значений признаков в диапазоны (), (), ().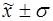

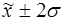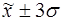4.    Дать сравнительную характеристику распределений единиц совокупности по двум изучаемым признакам на основе анализа:

а) вариации признаков;

б) количественной однородности единиц;

в) надежности (типичности) средних значений признаков;

г) симметричности распределений в центральной части ряда.

5.    Построить интервальный вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и установить характер (тип) этого распределения. Рассчитать моду Мо полученного интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.

Статистический анализ  генеральной совокупности

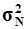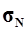1.               Рассчитать генеральную дисперсию , генеральное среднее квадратическое отклонение  и ожидаемый размах вариации признаков R_N. Сопоставить значения этих показателей для генеральной и выборочной дисперсий.

2.               Для изучаемых признаков рассчитать:

а) среднюю ошибку выборки;

б) предельные ошибки выборки для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут находиться средние значения признака генеральной совокупности при заданных уровнях надежности.

3.               Рассчитать коэффициенты асимметрии As и эксцесса Ek. На основе полученных оценок  сделать вывод о степени близости распределения единиц генеральной совокупности к нормальному распределению.