Содержание
|
Введение……………………………………………………………………
|
3
|
|
1.
|
Постановка
проблемы……………………………………………………..
|
4
|
|
1.1. Представление
данных……………………………………………….
|
4
|
|
1.2. Коэффициент
корреляции………...………………………………….
|
4
|
|
1.3. Интерпретация коэффициента
корреляции…………………………
|
5
|
|
2.
|
Результаты
эксперимента…………………………………………………
|
5
|
|
Выводы.
Заключение……………………………………………………...
|
12
|
|
Список
литературы………………………………………………………..
|
13
|
Введение
Любой современный психолог, независимо от того, является ли он психологом–практиком
или занимается теоретическими изысканиями, должен в совершенстве владеть
математическими методами и приёмами. Эти методы необходимы, во-первых, для
статистической обработки результатов психологического исследования, во-вторых,
для планирования эксперимента и прогнозирования ожидаемых результатов, наконец,
в-третьих, для разработки и построения математических моделей различных
психических явлений, процессов и состояний.
Интерпретация экспериментальных данных, как правило, несёт на
себе отпечаток личности психолога, его опыта, интуиции и т.д. В этом смысле
математика представляет собой универсальный язык, однозначно описывающий
различные свойства, признаки, изменения и прочее, в том числе и результаты
психологического исследования.
Мы рассмотрим один из наиболее применяемых методов исследования
меры связи – коэффициент корреляции.
Цель:
исследовать связь между осмысленностью жизни по Тесту смысложизненных
ориентаций и уровнем тревожности по Модифици-рованному восьмицветовому тесту
Люшера (Собчик Л.Н.)
Задачи:
1) вычислить коэффициент корреляции между уровнем осмысленности жизни и
уровнем тревожности;
2) сделать вывод о наличии или отсутствии достоверной связи между
исследуемыми характеристиками.
Гипотеза:
Н0 – Корреляция между уровнем
осмысленности жизни и уровнем тревожности не отличается от нуля.
Н1
– Корреляция между уровнем осмысленности жизни и уровнем тревожности достоверно
отличается от нуля.
1. Постановка проблемы
Многие психологические черты,
свойства, признаки встречаются не изолированно друг от друга, а определенным
образом взаимосвязаны между собой. Поэтому психологу часто приходится иметь
дело с выявлением связи между этими признаками, свойствами, чертами и т.д. Это
позволяет в известной степени минимизировать число изучаемых признаков
(особенно в тех случаях, когда их число достаточно велико.
В математическом смысле задача
состоит в нахождении связи между двумя рядами переменных (X и Y) в тех случаях, когда изменение величины
X ведет к
закономерному изменению величины Y. Если характер изменений предсказуем, можно говорить о
корреляции между этими переменными.
1.1 Представление данных
Данные о связи двух переменных могут быть
представлены либо графически (в виде диаграмм рассеивания), либо путем
вычисления коэффициентов корреляции по соответствующим формулам. В графическом
изображении каждый испытуемый может быть представлен точкой в координатах (X, Y), причем
величины X и Y соответствуют значениям двух исследуемых признаков.
1.2. Коэффициент корреляции
Исходный принцип коэффициента корреляции – использование
произведений моментов:
(x1-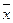
)*(y1-
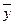)+…+(xn-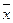)*(yn -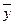)=å(xi -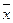)*(yi -)
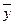Если сумма произведения моментов велика и положительна, то X и Y связаны прямой зависимостью; если
сумма велика и отрицательна, то X и Y сильно связаны обратной зависимостью; наконец, в случае
отсутствия связи между X и Y сумма произведений моментов близка к нулю.
Достоверность коэффициента корреляции можно определять по
соответствующим таблицам, не вычисляя ошибки. Если экспериментально полученное
значение r превышает табличное для данной выборки, коэффициент считается
статистически значимым.
1.3. Интерпретация
коэффициента корреляции
1. Корреляционная связь далеко не всегда
означает связь причинно-следственную.
2. rxy
около 0 может наблюдаться не
только при отсутствии связи между X и Y, но и в случае сильной нелинейной
связи.
3. rxy может быть достаточно мал, если
сильная связь между X и Y наблюдается
в более узком диапазоне значений, чем исследуемый.
4. Объединение выборок с различными
средними значениями может создавать иллюзию достаточно высокой корреляции.
2. Результаты
эксперимента
Психодиагностическое обследование было предложено лицам
пожилого возраста, прикованным к постели или с трудом передвигающимся по
комнате, с различными соматическими заболеваниями. Большинство из них – одиноко
проживающие.
У 20 испытуемых, протестированных с помощью Теста смысложизненных
ориентаций (см. Таблица 1), одним из исследуемых параметров был уровень осмысленности
жизни. Эти же испытуемые были обследованы с помощью Модифици-рованного
восьмицветового теста Люшера (см. Таблица 2).
В своих исследованиях с помощью Модифицированного
восьмицветового теста Люшера мы использовали второй выбор, так как он является
более спонтанным и поэтому более валидным, чем первый. В процессе интерпретации
обратили на себя некоторые особенности распределения цветов в выборах
участников. Психологически (частично или полностью осознанный конфликт между
желаемым и возможным) или физиологический
Таблица 1
Результаты Теста смысложизненных ориентаций
|
№
участника
|
Осмысленность
жизни
|
Цель
|
Процесс
|
Результат
|
ЛК-Я
|
ЛК-жизнь
|
|
1
|
107
|
34
|
31
|
29
|
16
|
31
|
|
2
|
106
|
40
|
21
|
23
|
26
|
35
|
|
3
|
134
|
42
|
42
|
30
|
27
|
41
|
|
4
|
87
|
32
|
22
|
24
|
19
|
20
|
|
5
|
103
|
40
|
28
|
27
|
16
|
31
|
|
6
|
87
|
39
|
26
|
21
|
21
|
25
|
|
7
|
102
|
40
|
26
|
23
|
21
|
26
|
|
8
|
99
|
40
|
18
|
28
|
22
|
28
|
|
9
|
88
|
34
|
19
|
26
|
18
|
27
|
|
10
|
77
|
36
|
15
|
20
|
12
|
20
|
|
11
|
84
|
29
|
21
|
21
|
18
|
36
|
|
12
|
104
|
38
|
24
|
28
|
23
|
30
|
|
13
|
63
|
14
|
12
|
12
|
15
|
20
|
|
14
|
81
|
28
|
20
|
18
|
17
|
14
|
|
15
|
86
|
38
|
30
|
22
|
13
|
18
|
|
16
|
63
|
27
|
22
|
15
|
14
|
13
|
|
17
|
91
|
39
|
25
|
22
|
16
|
27
|
|
18
|
93
|
33
|
16
|
27
|
16
|
35
|
|
19
|
100
|
36
|
30
|
22
|
19
|
29
|
|
20
|
86
|
36
|
25
|
21
|
19
|
20
|
Таблица 2
Результаты Модифицированного
восьмицветового теста Люшера
|
№
участника
|
критерии
второго выбора
|
уровень
тревожности
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
5
|
2
|
3
|
6
|
4
|
1(!)
|
0
|
7
|
1
|
|
2
|
2
|
4
|
0(!)
|
1
|
3
|
7
|
5
|
6
|
1
|
|
3
|
3
|
5
|
4
|
6
|
2
|
0
|
1(!!)
|
7
|
2
|
|
4
|
5
|
3
|
2
|
6
|
1
|
4(!)
|
0
|
7
|
1
|
|
5
|
4
|
3
|
5
|
2
|
6
|
0
|
1(!!)
|
7
|
2
|
|
6
|
4
|
2
|
5
|
3
|
0
|
6
|
1(!!)
|
7
|
2
|
|
7
|
2
|
3
|
0(!)
|
4
|
7
|
6
|
5
|
1(!!!)
|
4
|
|
8
|
6(!!!)
|
1
|
0(!)
|
7
|
2
|
3(!)
|
5
|
4(!!!)
|
8
|
|
9
|
2
|
6(!!)
|
5
|
0
|
4
|
3(!)
|
7
|
1(!!!)
|
6
|
|
10
|
4
|
3
|
0(!)
|
5
|
6
|
2(!)
|
1(!!)
|
7
|
4
|
|
11
|
3
|
5
|
6(!)
|
7
|
2
|
4(!)
|
0
|
1(!!!)
|
5
|
|
12
|
2
|
7(!!)
|
5
|
4
|
0
|
3(!)
|
6
|
1(!!!)
|
6
|
|
13
|
0(!!!)
|
7(!!)
|
4
|
1
|
6
|
2(!)
|
5
|
3(!!!)
|
9
|
|
14
|
0(!!!)
|
6(!!)
|
2
|
1
|
7
|
4(!)
|
5
|
3(!!!)
|
9
|
|
15
|
4
|
2
|
3
|
6
|
5
|
1(!)
|
0
|
7
|
1
|
|
16
|
5
|
2
|
4
|
1
|
0
|
6
|
3(!!)
|
7
|
2
|
|
17
|
2
|
5
|
4
|
3
|
1
|
6
|
7
|
0
|
0
|
|
18
|
5
|
2
|
6(!)
|
4
|
3
|
0
|
1(!!)
|
7
|
3
|
|
19
|
5
|
3
|
6(!)
|
4
|
0
|
2(!)
|
1(!!)
|
7
|
3
|
|
20
|
2
|
3
|
5
|
0
|
4
|
1(!)
|
6
|
7
|
1
|
стресс (чаще – неосознаваемая
эмоциональная напряженность, трансформированная в вегетативный и
функционально-организменный дисбаланс), считается относительно слабым, когда
основной цвет находится на 6-м месте, и более выраженным, если он на 8-м.
Интенсивность тревоги при напряженности и в стрессе измеряется количеством
знаков «!».
Задача состоит в том, чтобы, используя
коэффициент корреляции, подтвердить одну из
выдвинутых нами гипотез: Н0 – корреляция между уровнем
осмысленности жизни и уровнем тревожности не отличается от нуля. Н1
– корреляция между уровнем осмысленности жизни и уровнем тревожности достоверно
отличается от нуля.
Согласно принятым условиям построим
график зависимости.
Расположение точек на графике
показывает, что зависимость между признаками слабая.
График зависимости между признаками
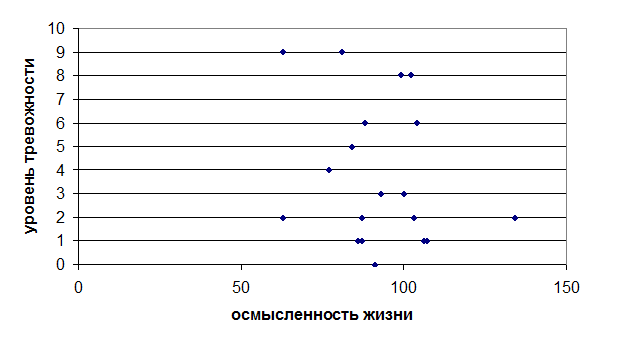
Для
оптимального расчета критериев описательной статистики и построения графиков
распределим, проранжируем показатели осмысленности жизни по интервалам (см.
Таблица 4).
С той же
целью проранжируем показатели уровня тревожности (см. Таблица 5).
Таблица 3
|
№
участника
|
Осмысленность
жизни
|
Тревожность
|
|
показатель
|
интервал
|
|
1
|
107
|
105
|
1
|
|
2
|
106
|
105
|
1
|
|
3
|
134
|
129
|
2
|
|
4
|
87
|
93
|
2
|
|
5
|
103
|
105
|
2
|
|
6
|
87
|
93
|
1
|
|
7
|
102
|
105
|
4
|
|
8
|
99
|
105
|
8
|
|
9
|
88
|
93
|
6
|
|
10
|
77
|
81
|
4
|
|
11
|
84
|
81
|
5
|
|
12
|
104
|
105
|
6
|
|
13
|
63
|
69
|
9
|
|
14
|
81
|
81
|
9
|
|
15
|
86
|
81
|
1
|
|
16
|
63
|
69
|
2
|
|
17
|
91
|
93
|
0
|
|
18
|
93
|
93
|
3
|
|
19
|
100
|
105
|
3
|
|
20
|
86
|
81
|
1
|
Таблица 4
|
№
|
Интервал
|
Количество
значений
|
Центральное
значение
|
|
1
|
63-74
|
1
|
69
|
|
2
|
75-86
|
4
|
81
|
|
3
|
87-98
|
5
|
93
|
|
4
|
99-110
|
7
|
105
|
|
5
|
111-122
|
2
|
117
|
|
6
|
123-134
|
1
|
129
|
Таблица 5
|
Уровень тревожности
|
|
Значение параметра
|
Частота встречаемости
|
|
1
|
5
|
|
2
|
4
|
|
3
|
2
|
|
4
|
1
|
|
5
|
1
|
|
6
|
1
|
|
7
|
1
|
|
8
|
1
|
|
9
|
2
|
График распределения значений уровня
осмысленности жизни
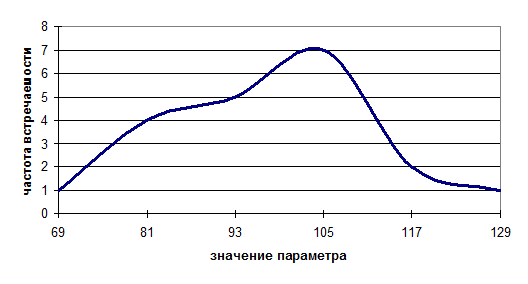
График распределения значений уровня тревожности
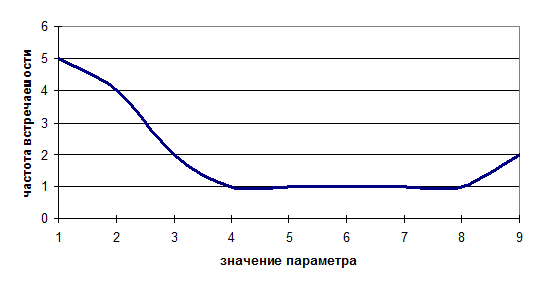
Таблица 6
|
Критерии описательной статистики
|
Осмысленность жизни
|
Уровень тревожности
|
|
Среднее
|
93,6
|
92,05
|
|
Стандартная ошибка
|
3,312178
|
3,589073
|
|
Медиана
|
93
|
89,5
|
|
Мода
|
105
|
87
|
|
Стандартное отклонение
|
14,81251
|
16,05082
|
|
Дисперсия выборки
|
219,4105
|
257,6289
|
|
Эксцесс
|
0,282911
|
1,613916
|
|
Асимметричность
|
0,269109
|
0,419237
|
|
Интервал
|
60
|
71
|
|
Минимум
|
69
|
63
|
|
Максимум
|
129
|
134
|
|
Сумма
|
1872
|
1841
|
|
Счет
|
20
|
20
|
Средне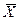е 
(или математическое ожидание М(Х)) – это среднее значение
случайной величины, которое рассчитывается по формуле:
.
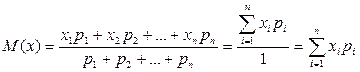Или иначе,
М(Х) – это сумма парных произведений случайной величины на соответствующую
вероятность.
Мода Мо(Х) распределения –
это значение случайной величины, имеющее наиболее вероятное значение.
Медиана Ме(Х) – это значение
случайной величины, которое делит таблицу распределения на две части таким
образом, что вероятность попадания в одну из них равна 0,5.
Стандартное отклонение (σ) – величина, представляющая собой
квадратный корень из несмещенной оценки дисперсии. Рассчитывается по формуле:
.
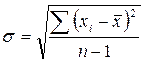Дисперсия (S2) – среднее арифметическое из квадратов отклонений
наблюдаемых значений случайной величины от их среднего арифметического.
Рассчитывается по формуле:
.
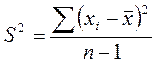Показатель асимметрии (А) высчитывается по
формуле:
.
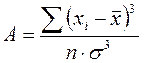В данном
случае асимметрия незначительная, положительная, левая.
Показатель эксцесса (Е) определяется по формуле:
.
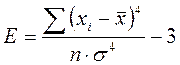В данном
случае: распределение значений уровня осмысленности жизни с положительным
эксцессом, а распределение значений уровня тревожности с отрицательным
эксцессом.
Сравнительный анализ
соотношения распределений
рассматриваемых значений
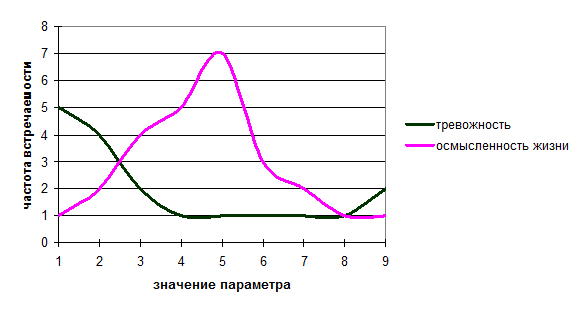
Для оценки
тесноты связи между признаками рассчитаем коэффициент корреляции между уровнем
осмысленности жизни и уровнем тревожности пожилых людей, принявших участие в
наших исследованиях.
Коэффициент корреляции рассчитывается по
формуле:
.
;
.
.
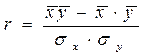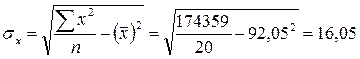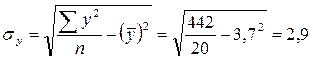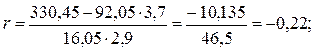
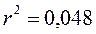Полученный коэффициент детерминации
показывает, что нет существенной зависимости между показателями уровня осмысленности
жизни и тревожности.
Таблица 7
Вспомогательная
таблица для расчета коэффициента корреляции
|
участник
|
х
|
у
|
х2
|
у2
|
ху
|
|
1
|
107
|
1
|
11449
|
1
|
107
|
|
2
|
106
|
1
|
11236
|
1
|
106
|
|
3
|
134
|
2
|
17956
|
4
|
268
|
|
4
|
87
|
2
|
7569
|
4
|
174
|
|
5
|
103
|
2
|
10609
|
4
|
206
|
|
6
|
87
|
1
|
7569
|
1
|
87
|
|
7
|
102
|
4
|
10404
|
64
|
816
|
|
8
|
99
|
8
|
9801
|
64
|
792
|
|
9
|
88
|
6
|
7744
|
36
|
528
|
|
10
|
77
|
4
|
5929
|
16
|
308
|
|
11
|
84
|
5
|
7056
|
25
|
420
|
|
12
|
104
|
6
|
10816
|
36
|
624
|
|
13
|
63
|
9
|
3969
|
81
|
567
|
|
14
|
81
|
9
|
6561
|
81
|
729
|
|
15
|
86
|
1
|
7396
|
1
|
86
|
|
16
|
63
|
2
|
3969
|
4
|
126
|
|
17
|
91
|
0
|
8281
|
0
|
0
|
|
18
|
93
|
3
|
8649
|
9
|
279
|
|
19
|
100
|
3
|
10000
|
9
|
300
|
|
20
|
86
|
1
|
7396
|
1
|
86
|
|
сумма
|
1841
|
74
|
174359
|
442
|
6609
|
|
средние
|
92,05
|
3,7
|
8717,95
|
22,1
|
330,45
|
Вывод. Заключение
Итак, коэффициент корреляции равен (– 0,022). Он показывает, что зависимость между уровнем осмысленности жизни и
уровнем тревожности статистически незначимо отличается от нуля. Таким образом,
подтвердилась нулевая гипотеза (Н0) – корреляция между уровнем
осмысленности жизни и уровнем тревожности не отличается от нуля. Альтернативная
гипотеза (Н1) – корреляция между уровнем осмысленности жизни и
уровнем тревожности достоверно отличается от нуля – не подтвердилась.
Коэффициент
детерминации (r2)
свидетельствует о том, что лишь 4,8% различий между уровнем осмысленности жизни и
уровнем тревожности являются взаимосвязанными, причем, учитывая
отрицательное значение коэффициента корреляции, можно предположить, что чем
выше осмысленность жизни, тем ниже уровень тревожности.
Список
литературы
1
Бочаров
П.П., Печинкин А.В. Теория вероятностей.
Математическая статистика. Н-ск Наука 1998г
2
Гмурман
В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.
Высшая школа 1999г
3
Лупандин
В.И. Математические методы в психологии 1997г
4
Немов
Р.С. Психология, книга 3-я М. Высшая школа 2001г
5
Сидоренко
Е.В. Методы математической обработки в психологии. СПб., 2002 г