ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Контрольная работа

По дисциплине

Финансовая математика

Вариант 2

Задание 1

В таблице приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство за 4 года (16 кварталов)

Требуется:

Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, применив параметры сглаживания α₁ = 0,3; α₂ = 0,6; α₃ = 0,3.

Оценить точность построенной модели с использованием средней ошибки аппроксимации;

Оценить адекватность построенной модели на основе исследования:

·                   случайности остаточной компоненты по критерию пиков;

·                   независимости уровней ряда остатков по d-критерию (в качестве критических использовать уровни d₁ = 1,10 и d₂ = 1,37) и по первому коэффициенту автокорреляции при критическом уровне значения r₁ = 0,32;

·                   нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.

Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

Отобразить на графиках фактические, расчетные и прогнозные данные.

Решение

Построим адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, применив параметры сглаживания α₁ = 0,3; α₂ = 0,6; α₃ = 0,3.

Для оценки начальных значений а(0) и b(0) применим линейную модель к первым 8 значениям Y(t).

Таблица 1

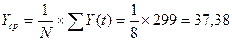
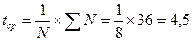
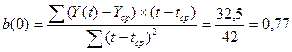
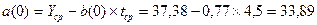
Получим линейное уравнение вида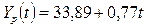

Для сопоставления фактических данных и рассчитанных по линейной модели значений составим таблицу.

Таблица 2

Сопоставление фактических и расчетных значений по линейной модели

Оценки коэффициентов сезонности для I – IV кварталов:

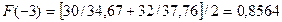
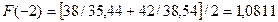
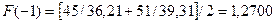
Таблица 3

Модель Хольта-Уинтерса

Проверка точности модели.

Таблица 4

Промежуточные расчеты для оценки адекватности модели

Суммарное значение относительных погрешностей составляет 34,9 Средняя величина: 34,9 / 16=2,18%, значит, условие точности выполнено, т.к. средняя величина относительных погрешностей не превышает 5%.

Проверка условия адекватности на основе исследования:

а) случайности остаточной компоненты по критерию пиков:

Условие случайности уровней ряда остатков выполнено, т.к. количество поворотных точек р = 10 > q = 6.

б) независимости уровней ряда остатков:

·                   по d- критерию Критерий Дарбина-Уотсона (критические уровни d₁=1,10 и d₂=1,37):

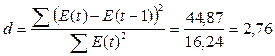
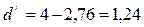
Так как 1,10<1,24<1,37, следовательно, уровни ряда Е(t) автокоррелированы, т. е. являются зависимыми.

·                   по первому коэффициенту автокорреляции r(1):

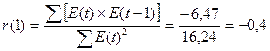
Уровни зависимы, т.к. критический уровень r_табл. = 0,32, а 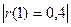> r_табл. = 0,32.

в) нормальности распределения остаточной компоненты по R/S-критерию:

E_max – E_min = 2,36 – (-1,63) = 3,99

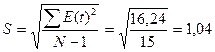
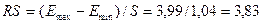
Уровни ряда остатков подчиняются нормальному распределению т.к. полученное значение RS (3,83) попадает в заданный интервал (3,00<3,83<4,21).

Произведем точечный прогноз на 4 шага вперед: Определим прогнозные значения экономического показателя Y_p(t) для: t = 17, 18, 19 и 20.

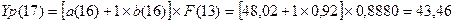
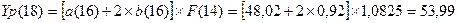
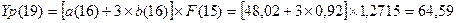
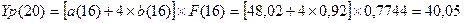
Отразим на графике фактические, расчетные и прогнозные данные (рис. 1).

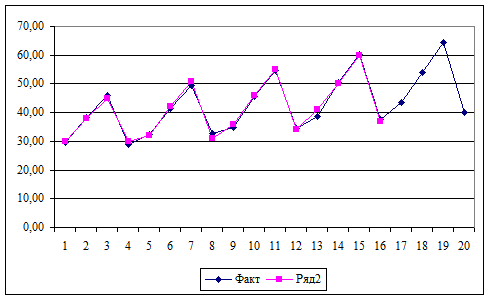
Рис. 1. Сопоставление расчетных и фактических данных

Задание 2

Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным 5 дням.

Рассчитать: экспоненциальную скользящую среднюю; момент; скорость изменения цен; индекс относительной силы; % R, % К, % D;

Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.

Решение

Экспоненциальную скользящую среднюю рассчитаем по формуле:

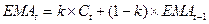, где k = 2 / (n + 1).

Момент:

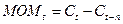
Скорость изменения цен:

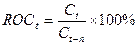
Таблица 1

Результаты расчетов экспоненциальной скользящей средней,

момента, скорости изменения цен

Индекс относительной силы рассчитаем по формуле:

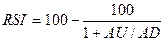
Таблица 2

Результаты расчета индекса относительной силы

%R рассчитаем по формуле:

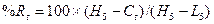
%К рассчитаем по формуле:

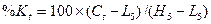
%D рассчитаем по формуле:

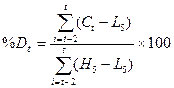
Таблица 3

Результаты расчетов %R, %К, %D

Задание 3

3.1. Банк выдал ссуду, размером 1 000 000 руб. Дата выдачи ссуды 18.01.02, возврата 12.03.02. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке 15% годовых.

Найти:

3.1.1) точные проценты с точным числом дней ссуды;

3.1.2) обыкновенные проценты с точным числом дней ссуды;

3.1.3) обыкновенные проценты с приближенным числом дней ссуды.

Решение

3.1.1) К = 365, t = 53, I = 1 000 000 х 0,15 х 53 / 365 = 2 1780,82 руб.

3.1.2) К = 360, t = 53, I = 1 000 000 х 0,15 х 53 / 360 = 2 2083,33 руб.

3.1.3) К = 360, t = 54, I = 1 000 000 х 0,15 х 54 / 360 = 2 2500,00 руб.

3.2. Через 180 дней после подписания договора должник уплатил 1 000 000 руб. Кредит выдан под 15% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

Решение

P = S / (1 + ni) = 1 000 000 / (1 + 0,15 х 180 / 360) = 930 232,56 руб.

D = S – P = 1 000 000 – 930 232,56 = 69 767,44 руб.

3.3. Через 180 предприятие должно получить по векселю 1 000 000 руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке 15% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

Решение

D = S_nd = 1 000 000 x 0,15 х 180 / 360 = 75 000,00 руб.

P = S – D = 1 000 000 – 75 000,00= 925 000,00 руб.

3.4. В кредитном договоре на сумму 1 000 000 руб. и сроком на 4 года, зафиксирована ставка сложных процентов, равная 15% годовых. Определить наращенную сумму.

Решение

S = P x (1+i)ⁿ = 1 000 000 х (1+0,15)⁴ = 1 749 006,25 руб.

3.5. Сумма размером 1 000 000 руб. представлена на 4 года. Проценты сложные, ставка 15% годовых. Проценты начисляются 2 раза в году. Вычислить наращенную сумму.

Решение

N = 4 x 2 = 8

S = P x (1+j / m)^N  = 1 000 000 х (1 + 0,15 / 2)⁸  = 1 783 477,83 руб.

3.6. Вычислить эффективную ставку процентов, если банк начисляет проценты 2 раза в год, исходя из номинальной ставки 15% годовых.

Решение

i_э = (1 + j / m)^m - 1 = (1 + 0,15 / 2)² – 1 = 0,1556, т.е. 15,5625%.

3.7. Определить, какой должна быть номинальная ставка при начислении процентов 2 раза в году, чтобы обеспечить эффективную ставку 15% годовых.

Решение

j = m x [(1 + i_э)^1/m - 1] = 2 x [(1 + 0,15)^(1/2) – 1] = 0,14476 т.е. 14,476%.

3.8. Через 4 года предприятию будет выплачена сумма 1 000 000 руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка 15% годовых.

Решение

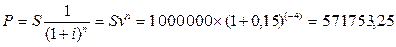 руб.

3.9. Через 4 года по векселю должна быть выплачена сумма 1 000 000 руб. Банк учел вексель по учетной ставке 15% годовых. Определить дисконт.

Решение

P = S (1 – d_сл)ⁿ = 1 000 000 x (1 – 0,15)⁴ = 522 006,25 руб.

D = S – P = 1 000 000 – 522 006,25 = 477 993,75 руб.

3.10. В течение 4 лет на расчетный счет в конце каждого года поступает по 1 000 000 руб., на которые 2 раза в году начисляются проценты по сложной годовой ставке 15%. Определить сумму на расчетном счете к концу указанного срока.

Решение

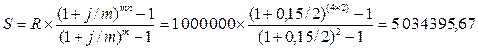 руб.