МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РФ
ВСЕРОССИЙСКИЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Кафедра
информатики и математики
Контрольная
работа
по
дисциплине:
«Эконометрика»
Исполнитель:
Факультет:
учетно-статистический
Специальность: бухгалтерский учет, анализ и аудит
Группа:
Номер личного дела:
г.
Уфа, 2008
Практическая
работа
Вариант 8
Задание:
1. Построение линейной модели регрессии
2. Построение
гиперболической модели
3. Построения
степенной модели
4. Построение
показательной модели
Решение:
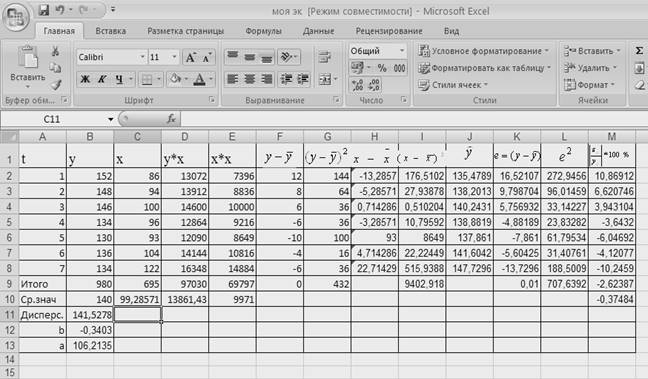 Таблица 1. Построение линейной
модели регрессии
Таблица 1. Построение линейной
модели регрессии
По данным таблицы 1 рассчитаем значения параметров
уравнения по формулам:
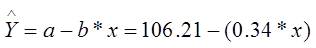 Уравнение
линейной регрессии:
Уравнение
линейной регрессии:
С увеличением объема капиталовложений
объем выпускаемой продукции уменьшится на 340 тыс. руб. это свидетельствует о
неэффективности работы предприятий.
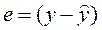 1) Остатки ( e )
рассчитаны в таблице по формуле:
1) Остатки ( e )
рассчитаны в таблице по формуле:
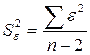 2) Дисперсия остатков
рассчитывается по формуле:
2) Дисперсия остатков
рассчитывается по формуле:
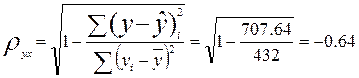 Индекс
корреляции:
Индекс
корреляции:
Рассчитаем коэффициент детерминации:
Вариация результата у объема выпуска
продукции на 164% объясняется вариацией фактора х объемом капиталовложений.
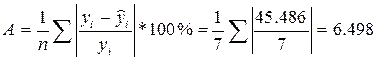 Рассчитаем среднюю относительную
ошибку:
Рассчитаем среднюю относительную
ошибку:
В среднем расчетное значение 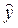 для
линейной модели отличается от фактических значений на 6,498 5%.
для
линейной модели отличается от фактических значений на 6,498 5%.
Оценку
значимости уравнения регрессии проведем с помощью F - критерия Фишера:
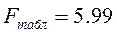 Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
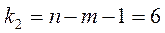
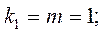
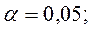
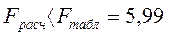 для
для
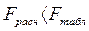 Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое, т.к.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое, т.к.
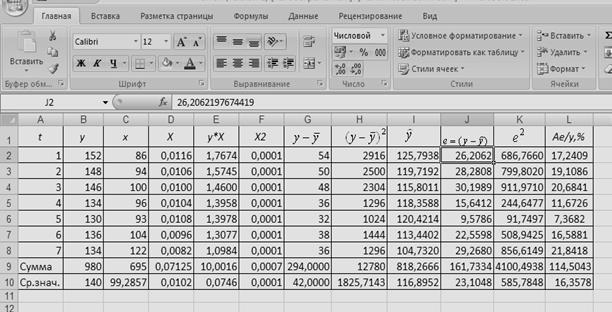
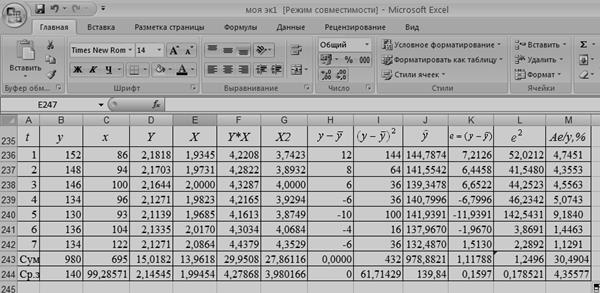
Таблица
2. Построение гиперболической модели
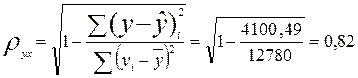 Индекс
корреляции:
Индекс
корреляции:
Рассчитаем коэффициент детерминации:
Вариация результата у объема выпуска
продукции на 164% объясняется вариацией фактора х объемом капиталовложений.
Рассчитаем среднюю относительную
ошибку:
В среднем расчетное значение 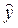 для линейной модели отличается от
фактических значений на 16,36%.
для линейной модели отличается от
фактических значений на 16,36%.
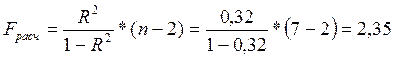 Оценку
значимости уравнения регрессии проведем с помощью F - критерия Фишера:
Оценку
значимости уравнения регрессии проведем с помощью F - критерия Фишера:
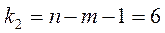
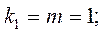
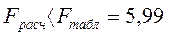
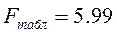 Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
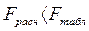
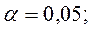 для
для
Уравнение регрессии с вероятностью 0,95
в целом статистически незначимое,
т.к.
 Таблица
3. Построения степенной модели
Таблица
3. Построения степенной модели
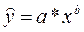 Уравнение степенной
модели имеет вид:
Уравнение степенной
модели имеет вид:
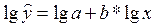 Преобразуем
в логарифмы:
Преобразуем
в логарифмы:
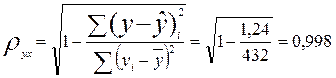 Индекс
корреляции:
Индекс
корреляции:
Рассчитаем коэффициент детерминации:
Вариация результата у объема выпуска
продукции на 164% объясняется вариацией фактора х объемом капиталовложений.
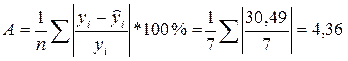 Рассчитаем среднюю относительную
ошибку:
Рассчитаем среднюю относительную
ошибку:
В среднем расчетное значение 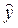 для линейной модели отличается от
фактических значений на 4,36%.
для линейной модели отличается от
фактических значений на 4,36%.
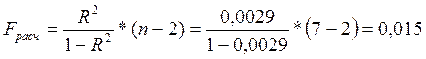 Оценку
значимости уравнения регрессии проведем с помощью F - критерия Фишера:
Оценку
значимости уравнения регрессии проведем с помощью F - критерия Фишера:
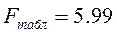
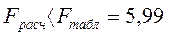 Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
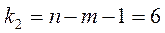
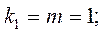
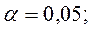 для
для
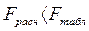 Уравнение регрессии с вероятностью
0,95 в целом статистически значимое,
т.к.
Уравнение регрессии с вероятностью
0,95 в целом статистически значимое,
т.к.
Таблица
4. Построение показательной модели
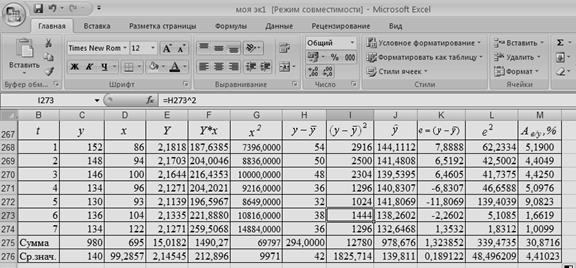
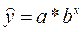 Уравнение показательной
кривой:
Уравнение показательной
кривой:
Преобразуем
в логарифмы:
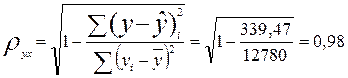 Индекс
корреляции:
Индекс
корреляции:
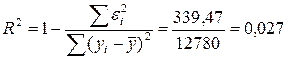 Рассчитаем коэффициент детерминации:
Рассчитаем коэффициент детерминации:
Вариация результата у объема выпуска
продукции на 164% объясняется вариацией фактора х объемом капиталовложений.
Рассчитаем среднюю относительную
ошибку:
В среднем расчетное значение 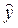 для линейной модели отличается от
фактических значений на 4,41%.
для линейной модели отличается от
фактических значений на 4,41%.
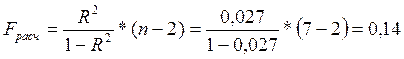 Оценку
значимости уравнения регрессии проведем с помощью F - критерия Фишера:
Оценку
значимости уравнения регрессии проведем с помощью F - критерия Фишера:
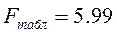
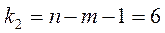 Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
Табличное
значение F - критерия Фишера при a=0,05 и k1=m=1? K2=n-m-1=6 равно:
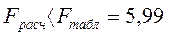
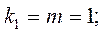
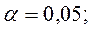 для
для
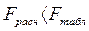 Уравнение регрессии с вероятностью
0,95 в целом статистически значимое,
т.к.
Уравнение регрессии с вероятностью
0,95 в целом статистически значимое,
т.к.