Введение
Математическая статистика – раздел математики,
который изучает методы сбора, систематизации, обработки результатов наблюдений
с целью выявления закономерностей. Математическая статистика опирается на
теорию вероятности.
Для
проведения эксперимента нами была выбрана группа студентов – 20 человек. Было
проведено исследование уровня агрессивности и уровня тревожности у испытуемых.
Методики
исследования:
1.
«Шкала тревожности» Д. Тейлор.
2.
Тест А. Ассингера (оценка агрессивности в отношениях)
Результаты исследования были обработаны с
использованием методов математической статистики.
Статистическая обработка полученных результатов
Сводная
таблица значений.
Х –
результат по «Шкале тревожности»
Y – результат теста Ассингера
|
№
|
х
|
y
|
х - хср
|
у – уср
|
(х - хср)2
|
(у – уср)2
|
ух
|
ху
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
20
|
34
|
-8,3
|
1,95
|
68,89
|
3,8
|
31,8
|
30
|
|
2
|
25
|
40
|
-3,3
|
4,05
|
10,89
|
16,4
|
34,3
|
32
|
|
3
|
18
|
20
|
-10,3
|
-15,95
|
106,09
|
254,4
|
30,8
|
13,9
|
|
4
|
40
|
41
|
11,7
|
5,05
|
136,89
|
25,5
|
41,8
|
32,8
|
|
5
|
35
|
37
|
6,7
|
1,05
|
44,89
|
1,1
|
39,3
|
29,2
|
|
6
|
46
|
47
|
17,7
|
11,05
|
313,29
|
122,1
|
44,8
|
38,2
|
|
7
|
15
|
21
|
-13,3
|
-14,95
|
176,89
|
223,5
|
29,3
|
14,8
|
|
8
|
21
|
35
|
-7,3
|
-0,95
|
53,29
|
0,9
|
32,3
|
27,4
|
|
9
|
29
|
41
|
0,7
|
5,05
|
0,49
|
25,5
|
36,3
|
32,8
|
|
10
|
36
|
40
|
7,7
|
4,05
|
59,29
|
16,4
|
39,8
|
32
|
|
11
|
39
|
35
|
10,7
|
-0,95
|
114,49
|
0,9
|
41,3
|
27,4
|
|
12
|
40
|
43
|
11,7
|
7,05
|
136,89
|
49,7
|
41,8
|
34,6
|
|
13
|
41
|
43
|
12,7
|
7,05
|
161,29
|
49,7
|
42,3
|
34,6
|
|
14
|
22
|
38
|
-6,3
|
2,05
|
39,69
|
4,2
|
32,8
|
30,1
|
|
15
|
17
|
22
|
-11,3
|
-13,95
|
127,69
|
194,6
|
30,35
|
15,7
|
|
16
|
30
|
36
|
1,7
|
0,05
|
2,89
|
0,003
|
36,8
|
28,3
|
|
17
|
25
|
39
|
-3,3
|
3,05
|
10,89
|
9,3
|
34,3
|
31
|
|
18
|
29
|
40
|
0,7
|
4,05
|
0,49
|
16,4
|
36,3
|
32
|
|
19
|
13
|
30
|
-15,3
|
-5,95
|
234,09
|
35,4
|
28,3
|
22,9
|
|
20
|
25
|
37
|
-3,3
|
1,05
|
10,89
|
1,1
|
34,3
|
29,2
|
Изначально
нам необходимо определить среднее арифметическое и дисперсию для результатов,
полученных по обоим методикам.
Среднее арифметическое является мерой центральных тенденций.
Это показатель, несущий характеристики наибольшей вероятности встречаемости.
Для нахождения среднего арифметического могут быть использованы следующие
способы:
1.
Необходимо умножить сумму произведений всех вариантов
на их веса.
2.
Необходимо сложить все значения и разделить полученное
число на количество наблюдений (испытуемых).
Количество
наблюдений (20) позволяет нам использовать второй вариант.
Дисперсия является мерой вариативности (разброса).. Среднее
арифметическое и дисперсия имеют смысл только для метрических переменных.
Среднее
арифметическое для значений х - хср.
Дисперсия
для значений х – δ2х.
Среднее
арифметическое для значений y – yср.
Дисперсия
для значений y - δ2y.
Среднее
арифметическое находим, согласно второму варианту (см. выше):
1.
Для значений х:
хср
= (х1 + х2 + х3 + … + хn) / n, где
х1,
х2, х3 , хn – значения
переменной х (результат тестирования),
n – количество наблюдений (в нашем
случае n=20).
хср = 28,3
Дисперсию
находим по формуле:
δ2х
= Σ (хr - хср)2
/ n, где
хr – значение переменной х (результат
тестирования),
хср
– среднее арифметическое от х,
n – количество наблюдений (в нашем
случае n=20).
δ2х = 94,499
2.Для
значений y:
yср = 35,95
δ2y = 52,5
Далее находим коэффициент корреляции между
значениями х и у, т.е. между тревожностью и агрессивностью в данной группе.
Другими словами, нам нужно выяснить, существует ли зависимость между уровнем
тревожности и уровнем агрессивности. Корреляционная зависимость – это
функциональная зависимость между значением одной переменной и условным математическим
ожиданием другой. Корреляционные связи не могут рассматриваться как
свидетельство причинно-следственной связи, они свидетельствуют лишь о том, что
изменениям одного признака, как правило, сопутствуют определенные изменения
другого.
Наши
переменные являются метрическими, следовательно, мы можем использовать
коэффициент корреляции Пирсона, который вычисляется по формуле:
R = Σ (х - хср) (у –
уср) / √ Σ (х - хср)2 (у – уср)2,
где
R – коэффициент корреляции,
Х
– значения, принимаемые переменной х,
Y – значения, принимаемые переменной
у,
хср
– среднее арифметическое от х,
уср
– среднее арифметическое от у,
Σ
– знак суммы,
√
- знак квадратного корня.
R = 0,727
Коэффициент
корреляции принимает значения от –1 до 1. Если коэффициент корреляции стремится
к -1 или 1, значит, между переменными существует зависимость. Если коэффициент
корреляции стремится к 1, то говорят о прямой зависимости, если к –1, то
говорят об обратной зависимости.
В
нашем случае коэффициент корреляции стремится к 1. Следовательно, между
переменными существует прямая зависимость. Другими словами, в выбранной группе
между уровнем агрессивности и уровнем тревожности существует определенная
связь, влияние. Корреляционная зависимость не позволяет нам говорить о причинах
и следствиях этой связи (что на что влияет), однако, мы выяснили, что
изменениям одного из признаков сопутствуют изменения другого признака.
Более
достоверные данные о существовании корреляционной зависимости мы можем
получить, определив критические значения переменных и эмпирическое значение.
Последнее определяется по формуле:
Tэмп = (R √ n – 2 ) /
√ (1 – R2), где
Tэмп –
эмпирическое значение коэффициента корреляции,
R – коэффициент корреляции,
√
- знак квадратного корня,
n – количество наблюдений (в нашем
случае n=20).
Tэмп = 18,7
Критические
значения мы определяем по таблице критических значений Стьюдента для уровней
значимости 0,05 и 0,01:
Т (0,05) = 1,81
Т
(0,01) = 2,35
Если эмпирическое значение превышает критическое,
то говорят о существовании зависимости между переменными. В нашем случае
эмпирическое значение значительно превышает оба критических, что подтверждает
сделанный нами ранее вывод: существует взаимосвязь уровня агрессивности и
уровня тревожности (для данной группы).
Теперь
выведем уравнение линейной регрессии. С его помощью мы можем
точнее определить вид зависимости, уже определенный нами ранее как «прямая».
Для
этого необходимо вычислить значения S2 для
значений х и у, значение выборочной ковариации м и значения выборочного
коэффициента корреляции в для значений ху и ух.
S2х = Σ
(х - хср)2 / n – 1
S2у = Σ
(у – уср)2 / n – 1, где
Σ
– знак суммы,
Х
– значения, принимаемые переменной х,
Y – значения, принимаемые переменной
у,
хср
– среднее арифметическое от х,
уср
– среднее арифметическое от у,
n – количество наблюдений (в нашем
случае n=20).
S2х = 99,5
S2у = 55,3
Значение
выборочной ковариации вычисляем по формуле:
М
= Σ (х - хср) (у – уср) / n, где
М
– выборочная ковариация,
Σ
– знак суммы,
Х
– значения, принимаемые переменной х,
Y – значения, принимаемые переменной
у,
хср
– среднее арифметическое от х,
уср
– среднее арифметическое от у,
n – количество наблюдений (в нашем
случае n=20).
М = 51,2
Выборочные
коэффициенты регрессии определяем по формулам:
Вху
= М / S2у = 0,9
Вух
= М / S2х = 0,5
Теперь
мы можем составить уравнение регрессии:
1.
ух - уср = Вух
(х - хср)
2.
ху - хср = Вху
(у – уср)
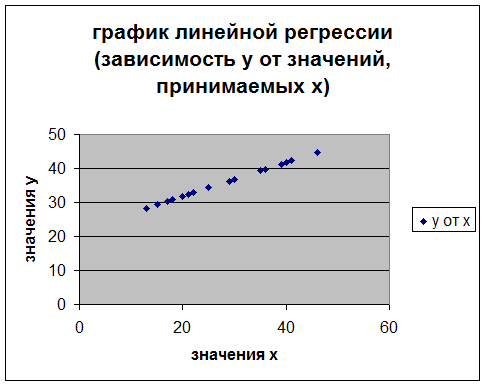
Значения,
которые принимает ух при различных значениях переменной х указаны в
столбце 7 сводной таблицы. Значения ху – в столбце 8 сводной
таблице. По этим значениям мы можем построить графики линейной регрессии.
Для 1-го
уравнения:
Для 2-го
уравнения:
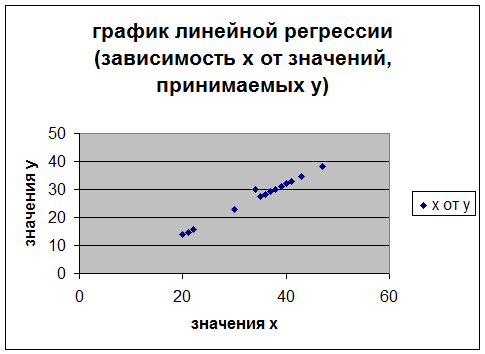
Подобное
распределение точек около прямой в виде эллипса свидетельствует о существовании
прямой линейной зависимости.
Вывод: в результате проведенного эксперимента и
математической обработки данных этого эксперимента мы можем говорить о том, что
для данная группа студентов характеризуется наличием связи между уровнем
агрессивности и уровнем тревожности.
Список литературы
1.
Сидоренко Е. Методы математической обработки в
психологии. СПб: Речь, 2002.
2.
Практическая психология. Инструментарий.
Ростов-на-Дону: Феникс, 2002.
3.
Немов Р.С. Психология. Т.3. М.: Владос, 2000.
4.
Психологические тесты. Т.2. / Под ред. А.А. Карелина.
М.: Владос, 2001.