Задание 1.

Высказано утверждение: «Размер заработной платы зависит от пола работника». Как можно проверить это утверждение?


Решение.

Для проверки этого утверждения можно использовать следующие методы:

1.     Посчитать средние арифметические заработной платы для мужчин и для женщин и сравнить их. Если средние арифметические заработной платы для мужчин и для женщин близки по значению, то утверждение неверно. Этот метод можно применить, если количество исследуемых работников велико.

2.     Посчитать медианы заработной платы  мужчин и женщин и сравнить их. Для этого нужно разделить шкалу   заработной платы  на интервалы и посчитать частоту попадания в каждый интервал. Затем посчитать накопленные частоты (сумму частот значений признака, не превосходящих какое-либо заданное значение)  и интегральный процент. Медиана – это значение признака, находящегося в середине совокупности: 50% значений признака меньше медианы, а 50% больше или равно. Медиана меньше, чем средняя арифметическая, зависит от формы распределения признака. Если медианы заработной платы для мужчин и для женщин близки по значению, то утверждение неверно. Этот метод можно применить, если количество исследуемых работников велико.

3.                Провести проверку гипотез о связи признаков «размер заработной платы» и «пол», применяя критерий Пирсона.  Размер заработной платы делится на интервалы, считаются значения пi – частоты  попадания в каждый интервал и составляется таблица сопряженности:


Пол

Размер заработной платы

1-й интервал

…

к-й интервал

итого

мужской

n1

…

nk

b1

женский

nk+1

…

n2k

b2

итого

a1

…

ak

S

Затем считаются значения 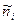  -  ожидаемые  частоты по правилу: .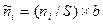

Проверочной статистикой является значение 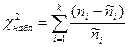. По таблице находим 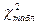. Если 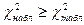, то зависимость между признаками существует.

Задание 2.

На рисунках 1 и 2 приведены результаты анализа распределения заработной платы на двух предприятиях. Что вы можете сказать об этих распределениях? Какие показатели можно использовать для их описания? Какие показатели вы можете оценить, опираясь только на приведенные рисунки (абсолютные значения, знаки, в сравнении друг с другом …)? Постарайтесь использовать максимальное число показателей и терминов.


Решение.

Данные распределения близки к нормальному.

Для их описания можно использовать следующие показатели: среднее, мода, медиана, асимметричность, дисперсия, стандартное отклонение, эксцесс.

Опираясь только на приведенные рисунки можно оценить параметры:

1.     Среднее.

Для первого предприятия среднее равно: (1000×3+1500×8+2000×11+2500×5+ +3000×4+3500×3+4000×2+4500×2+5000×1)/(3+8+11+5+4+3+2+2+1)=94000/39=2410,3.

Для второго предприятия среднее равно: (1000×1+1500×1+2000×3+2500×3+ 3000×4+3500×5+4000×11+4500×8+5000×3)/(1+1+3+3+4+5+11+8+3)=140500/39=

=3602,6.

2.     Мода – наиболее часто встречающееся значение.

Для первого предприятия мода равна 2000 руб.

Для второго предприятия мода равна 4000 руб.

3.                Медиана – это значение признака, находящегося в середине совокупности: 50% значений признака меньше медианы, а 50% больше или равно.

Для первого предприятия медиана равна 2000 руб.

Для второго предприятия медиана равна 3500 руб.

4.     Асимметричность говорит о сдвиге вершины распределения влево или вправо от среднего значения.

Для первого предприятия асимметричность положительна. Положительная асимметрия означает, что большинство сотрудников в организации получает зарплату меньше средней.

Для второго предприятия асимметричность отрицательна. Отрицательная асимметрия означает, что большинство сотрудников в организации получает зарплату больше средней.






Задание 3.

Высказано утверждение: «Размер заработной платы зависит от стажа работы». Как облечь это утверждение в форму эконометрической модели? Как можно проверить это утверждение?


Решение.

Эконометрическая модель:

Требуется выяснить, существует ли связь между случайной величиной Х – «стаж работы» и случайной величиной Y – «размер заработной платы». Для этого необходимо оценить тесноту связи между Х и Y.

По исходным данным значений Х и Y вычисляется коэффициент корреляции, принимающий значения от –1 до 1.

Для вычисления коэффициента корреляции находят выборочные средние и среднеквадратические отклонения переменных Х и Y по формулам:

,   ,  ,  .

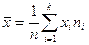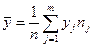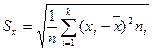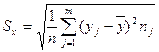Коэффициент корреляции вычисляется по формуле:

.

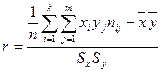Если абсолютное значение коэффициента корреляции близко к 1, то связь между признаками тесная. Близость коэффициента корреляции к 0 говорит об отсутствии связи между признаками. Задание 4.

Имеются данные о времени доставки продукции на различные расстояния. Был проведен анализ, результаты которого приведены на рисунке 3. Подробно объясните, что проделал исследователь, что получилось в результате и как эти результаты можно использовать?


Решение.

Исследователь построил в табличном процессоре Excel точечную диаграмму зависимости времени доставки продукции (у) от  расстояния (х). Затем к полученному графику была добавлена линия тренда. На диаграмме показано уравнение линейного тренда у = 2,6597х+5,9135. Коэффициент 2,6597 показывает, что при увеличении расстояния на 1 км время доставки увеличивается в среднем на 2,6597 мин. С его помощью можно прогнозировать время доставки продукции в новые пункты (подставить вместо х расстояние и вычислить значение у – требуемое для доставки время). Также на диаграмме показан коэффициент детерминации R2 = 0,9183, показывающий, что вариация времени на 91,83% объясняется изменчивостью расстояния, что говорит о сильной зависимости времени доставки от расстояния.

 

Задание 5.

Приведите данные, касающиеся вашей работы, для которых можно использовать метод, применённый в задании 4. Опишите содержательную задачу, ожидаемый результат и как его можно использовать?


Решение.

Задача. Имеются данные о количестве назначений в палаты, содержащие различные количества больных. Требуется составить уравнение линейной регрессии и оценить тесноту связи между данными показателями.

Число больных

в палате

Количество

назначений

1

3

1

4

2

7

2

5

3

9

4

11

6

17

6

19

7

20

8

25

Ожидаемый результат:

Уравнение линейной регрессии зависимости количества назначений в палаты от числа больных в палате. Коэффициент при х в уравнении регрессии показывает на сколько увеличивается число назначений при увеличении больных в палате на 1 человека.

Коэффициент детерминации, близкий к 1, показывающий, что между количеством назначений в палаты и числом больных в палате существует тесная связь.

 Использование результата: Для прогнозирования количества назначений в новые палаты.

Задание 6.

Имеются данные о динамике выпуска продукции неким предприятием. На рисунке 4 приведены результаты анализа. Подробно объясните, что проделал исследователь, что получилось в результате и как эти результаты можно использовать?


Решение.

Исследователь построил в табличном процессоре Excel точечную диаграмму зависимости выпуска продукции (у) от  года (х). Затем к полученному графику была добавлена линия экспоненциального тренда. На диаграмме показано уравнение тренда у = 677,64е0,0866х. С его помощью можно прогнозировать выпуск продукции в последующие годы (подставить вместо х номер года и вычислить значение у – ожидаемый выпуск продукции). Также на диаграмме показан коэффициент детерминации R2 = 0,9999, показывающий, что вариация выпуска продукции на 99,99% объясняется изменением года, что говорит о сильной зависимости выпуска продукции от года.

 

Задание 7.

Имеются данные о динамике продаж некоторой продукции. На рисунке 5 приведены результаты анализа. Подробно объясните, что проделал исследователь, какие методы можно применить, что получилось в результате и  как эти результаты можно использовать?


Решение.

Исследователь построил в табличном процессоре Excel график зависимости объема продаж продукции (у) от  квартала (х). Затем к полученному графику была добавлена линия тренда. На диаграмме показано уравнение линейного тренда у = 20,978х+176,31. С его помощью можно прогнозировать объем продаж продукции в последующие кварталы (подставить вместо х номер квартала и вычислить значение у – ожидаемый объем продаж продукции). Также на диаграмме показан коэффициент детерминации R2 = 0,7666, показывающий, что вариация объема продаж продукции на 76,66% объясняется изменением номера квартала что говорит о не очень сильной зависимости объема продаж продукции  от  квартала.

На графике явно видны сезонные колебания объема продаж внутри года. Для исследования  сезонности рассчитывается индекс сезонности – отношение уровня квартала к среднеквартальному уровню. Так как объем продаж снижается к середине года и возрастает к концу, то  сезонные колебания являются вогнутыми. Расчеты сезонных колебаний можно провести с помощью ряда Фурье.



 

Задание 8.

Приведите данные, касающиеся вашей работы, для которых можно использовать метод, применённый в задании 7. Опишите содержательную задачу, ожидаемый результат и как его можно использовать?


Решение.

Задача:

В инфекционное отделение поступают больные с простудными заболеваниями (ОРЗ, ОРВИ, ангина, бронхит, пневмония) и больные с другими заболеваниями (желудочно-кишечные, скарлатина и др.). Имеются данные по кварталам процента   больных с простудными заболеваниями от общего числа поступивших больных. Требуется:

1. Построить график динамики процента   больных с простудными заболеваниями.

2.                Составить уравнение линейной регрессии.

3.                Оценить тесноту связи между данными показателями.

4.                 Исследовать сезонные колебания с помощью индексов сезонности.

5.                Рассчитать сезонные колебания с помощью ряда Фурье.


Период

Процент больных

простудными заболеваниями

Янв.-Март   2002

59

Апр.-Июнь

53

Июль-Сент.

47

Окт. –Дек.

56

Янв.-Март  2003

62

Апр.-Июнь

51

Июль-Сент.

45

Окт. –Дек.

68

Ожидаемый результат:

1. График динамики процента   больных с простудными заболеваниями, наглядно показывающий наличие сезонных колебаний внутри года.

2. Уравнение линейной регрессии зависимости процента   больных с простудными заболеваниями от общего числа поступивших больных от квартала.

3. Коэффициент детерминации, близкий к 1, показывающий, что между процентом   больных с простудными заболеваниями от общего числа поступивших больных и кварталом существует тесная связь.

4. Расчет индексов сезонности, подтверждающих наличие сезонных колебаний  процента   больных с простудными заболеваниями внутри года.

 5. Составление ряда Фурье: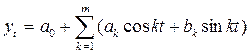  

Использование результата:

Для прогнозирования процента   больных с простудными заболеваниями от общего числа поступивших больных в новые кварталы.