Контрольная работа

Вариант №5

 

Задача №1

По предприятиям легкой промышленности региона получена информация характеризующая зависимость объема выпуска продукции (Y, млн.руб.)от объема капиталовложений (Х, млн.руб.).

Требуется:

1.                Для характеристики Y от Х построить следующие модели:

- линейную,

- степенную,

- показательную,

- гиперболическую.

2. Оценить каждую модель, определив:

         - индекс корреляции,

         - среднюю относительную ошибку,

         - коэффициент детерминации,

         - F-критерий Фишера.

3. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.

4. рассчитать прогнозные значения результативного признака, если прогнозное значение фактора увеличится на 110% относительно среднего уровня.

5. Результаты расчетов отобразить на графике.

Задание к задаче№1

y	32	40	44	47	50	56	50
х	60	68	80	76	74	87	96

Решение:

1.     Построение линейной модели парной регрессии

Для расчетов нам понадобятся некоторые расчетные значения, которые приведены в следующей таблице:

t	y	x	y*x	x*x	(yi-yср)	(yi-yср)2	(xi-xср)	(xi-xср)2	yрасч	ei=yi-yi расч	|ei/yi|*100%	(y-yср)*(x-xср)
1	32	60	1920	3600	-13,57	184,184	-17,29	298,796	36,417	-4,417	13,803	234,592
2	40	68	2720	4624	-5,57	31,041	-9,29	86,224	40,654	-0,654	1,634	51,735
3	44	80	3520	6400	-1,57	2,469	2,71	7,367	47,009	-3,009	6,838	-4,265
4	47	76	3572	5776	1,43	2,041	-1,29	1,653	44,891	2,109	4,488	-1,837
5	50	74	3700	5476	4,43	19,612	-3,29	10,796	43,831	6,169	12,337	-14,551
6	56	87	4872	7569	10,43	108,755	9,71	94,367	50,716	5,284	9,436	101,306
7	50	96	4800	9216	4,43	19,612	18,71	350,224	55,483	-5,483	10,965	82,878
ИТОГО	319	541	25104	42661	0,01	367,714		849,429		-0,02	59,502	449,857
среднее	45,57	77,29	3586,29	6094,43							8,500

      Определим коэффициент парной корреляции по следующей формуле:

                                      ________________

r_y,x = ∑(y-y_ср)*(х-х_ср)/√ ∑(y-y_ср)²*(х-х_ср)²

r_y,x = 0,805

Можно сказать что связь между объемом капиталовложений Х и объемом выпуска продукции Y обратная, достаточно сильная.

Уравнение линейной регрессии имеет вид: у_расч = a + b*x

Параметры a и b рассчитываются по формулам:

       ___     _  _   _     _₂

b =( у*х – у*х)/(х² – х ); b = 0,53

      _        _

а = у – b*х ; а = 4,64

Уравнение линейной регрессии имеет вид: у_расч = 4,64 + 0,53*x

Рассчитаем коэффициент детерминации R²

R² = r²_y,x

R² =0,648

Вариация результата Y (объема выпуска продукции) на 64,8 % объясняется вариацией фактора Х (объемом капиталовложений).

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

            R² *(n-2)

F_расч  =   1- R²

F_расч = 9,201

F_табл = 6,608 для ά=0,05; k₁=m=1;k₂=n-m-1=5

F_расч > F_табл

Уравнение регрессии с вероятностью 0.95 в целом статистически значимо т.к. F_расч > F_табл.

Определим среднюю относительную ошибку:             

Е_отн =  1/ n _*∑ | Ei/у|

Е_отн = 8,5

В среднем расчетные значения у_расч для линейной модели отличаются от фактических значений на 8,5%

2.     Построение степенной модели парной регрессии

Уравнение степенной модели имеет вид: у_расч = a*x^b

Для построения этой модели необходимо провести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения: lg y_расч = lg a + b lg x.

	Факт.y (t)	lg (y)	Переменная x (t)	lg x
1	32	1,505	60	1,778
2	40	1,602	68	1,833
3	44	1,643	80	1,903
4	47	1,672	76	1,881
5	50	1,699	74	1,869
6	56	1,748	87	1,940
7	50	1,699	96	1,982
28	319	11,569	541	13,1856
Среднее	45,571	1,653	77,286	1,884

Обозначим Y = lg y; X = lg x; A = lg a.

Тогда уравнение примет вид Y = A + b*X – линейное уравнение регрессии.

Рассчитаем его параметры используя следующую таблицу:

t	y	Y	x	X	Y*X	X*X	Yрасч	E	|Ei/yi|*100%	E2	(y-yср)2
1	32	1,505	60	1,778	2,676	3,162	35,264	-3,264	10,199	10,652	184,184
2	40	1,602	68	1,833	2,936	3,358	39,959	0,041	0,102	0,002	31,041
3	44	1,643	80	1,903	3,128	3,622	47,001	-3,001	6,821	9,007	2,469
4	47	1,672	76	1,881	3,145	3,537	44,654	2,346	4,991	5,504	2,041
5	50	1,699	74	1,869	3,176	3,494	43,480	6,520	13,039	42,506	19,612
6	56	1,748	87	1,940	3,391	3,762	51,108	4,892	8,735	23,929	108,755
7	50	1,699	96	1,982	3,368	3,929	56,388	-6,388	12,777	40,811	19,612
ИТОГО	319	11,569	541	13,186	21,819	24,864	317,855	1,145	56,664	132,409	367,714
среднее	45,57	1,65	77,29	1,88	3,12	3,55			8,09	18,92

        ____   __  __    __     __₂

b =( Y*X – Y * X )/(X² – X ); b = 0,999

      _        _

A = Y – b*Y ; а = -0, 229

Уравнение регрессии имеет вид: Y_расч = -0,229 + 0,999*X

Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения.

у_расч = 10^-0,229 *х^0,999

Получим уравнение степенной модели у_расч = 0,591* х^0,999

    

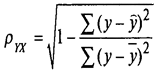
ρ_y,x = 0,8

Связь между показателем у и фактором х можно считать достаточно сильной.

Рассчитаем коэффициент детерминации R²

R² = ρ²_y,x

R² =0,64

Вариация результата Y (объема выпуска продукции) на 64 % объясняется вариацией фактора Х (объемом капиталовложений).

Рассчитаем F-критерий Фишера:

            R² *(n-2)

F_расч  =   1- R²

F_расч = 8,886

F_табл = 6,608 для ά=0,05; k₁=m=1;k₂=n-m-1=5

F_расч > F_табл

Уравнение регрессии с вероятностью 0.95 в целом статистически значимо т.к. F_расч > F_табл.

Определим среднюю относительную ошибку:             

Е_отн =  1/ n _*∑ | Ei/у|

Е_отн = 8,095

В среднем расчетные значения у_расч для степенной модели отличаются от фактических значений на 8,09%

3.     Построение показательной функции

Уравнение степенной модели имеет вид: у_расч = a*b^x

Для построения этой модели необходимо провести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения: lg y_расч = lg a + x lg b.

Обозначим Y = lg y; B = lg b; A = lg a.

Тогда уравнение примет вид Y = A + B*x – линейное уравнение регрессии.

Рассчитаем его параметры используя следующую таблицу:

t	y	Y	x	Y*х	х2	Y-Yср	(Y-Yср)2	x-xср	(x-xср)2	Yрасч	E=y-Yрасч	|Ei/yi|*100%	E2	(y-yср)2
1	32	1,5051	60	90,31	3600	-0,1475	0,0218	-17,29	298,80	36,2	-4,211	13,16	17,733	184,18
2	40	1,6021	68	108,94	4624	-0,0506	0,0026	-9,29	86,22	40,0	-0,020	0,05	0,0004	31,04
3	44	1,6435	80	131,48	6400	-0,0092	0,0001	2,71	7,37	46,5	-2,498	5,68	6,2410	2,47
4	47	1,6721	76	127,08	5776	0,0194	0,0004	-1,29	1,65	44,2	2,770	5,89	7,6727	2,04
5	50	1,6990	74	125,72	5476	0,0463	0,0021	-3,29	10,80	43,1	6,862	13,72	47,0901	19,61
6	56	1,7482	87	152,09	7569	0,0955	0,0091	9,71	94,37	50,8	5,249	9,37	27,5523	108,76
7	50	1,6990	96	163,10	9216	0,0463	0,0021	18,71	350,22	56,8	-6,795	13,59	46,1754	19,61
ИТОГО	319	11,5689	541	898,72	42661		0,0382		849,4		1,356	61,47	152,4651	367,71
среднее	45,57	1,6527	77,29	128,39	6094							8,78	21,7807

        ____   __  __   __    _₂

B =( Y*x – Y * x )/(x² – x ); B = 0,0054

        _         _

A = Y – B*x ; A = 1,23

Уравнение регрессии имеет вид: Y_расч = 1,23 + 0,0054*x

Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения.

                                    _x

у_расч = 10^1,23 *10 ^0,0054   

Получим уравнение показательной модели у_расч = 17,102* 1,0126 ^x

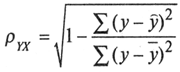
ρ_y,x = 0,7651

Связь между показателем у и фактором х можно считать достаточно сильной.

Рассчитаем коэффициент детерминации R²

R² = ρ²_y,x

R² =0,5854

Вариация результата Y (объема выпуска продукции) на 64 % объясняется вариацией фактора Х (объемом капиталовложений).

Рассчитаем F-критерий Фишера:

            R² *(n-2)

F_расч  =   1- R²

F_расч = 7,059

F_табл = 6,608 для ά=0,05; k₁=m=1;k₂=n-m-1=5

F_расч > F_табл

Уравнение регрессии с вероятностью 0.95 в целом статистически значимо т.к. F_расч > F_табл.

Определим среднюю относительную ошибку:             

Е_отн =  1/ n _*∑ | Ei/у|

Е_отн = 8,781

В среднем расчетные значения у_расч для показательной модели отличаются от фактических значений на 8,78%

4.     Построение гиперболической функции

Уравнение степенной модели имеет вид: у_расч = a+b/x

Проведем линеаризацию модели путем замены Х = 1/х.

В результате получим линейное уравнение у = a + b*X.

Рассчитаем его параметры используя следующую таблицу:

t	y	x	Х	y*X	X2	y-yср	(y-yср)2	Yрасч	E=y-Yрасч	|Ei/yi|*100%	E2
1	32	60	0,0167	0,5333	0,0002778	-13,57	184,18	34,3	-2,338	7,31	5,4678
2	40	68	0,0147	0,5882	0,0002163	-5,57	31,04	40,7	-0,722	1,81	0,5214
3	44	80	0,0125	0,5500	0,0001563	-1,57	2,47	47,9	-3,904	8,87	15,2393
4	47	76	0,0132	0,6184	0,0001731	1,43	2,04	45,8	1,238	2,63	1,533
5	50	74	0,0135	0,6757	0,0001826	4,43	19,61	44,6	5,396	10,79	29,1162
6	56	87	0,0115	0,6437	0,0001321	10,43	108,76	51,2	4,822	8,61	23,2501
7	50	96	0,0104	0,5208	0,0001085	4,43	19,61	54,7	-4,686	9,37	21,96
ИТОГО	319	541	0,0925	4,1302	0,0012467		367,71	319,2	-0,195	49,39	97,091
среднее	45,57	77,29	0,0132	0,5900	0,0001781					7,056

       ____   __  __   __      _₂

b =( y*X – y * X )/(X² – X ); b = -3255,7

      _         _

a = у – b*X ; а = 88,6

Уравнение гиперболической модели имеет вид: у_расч = 88,6 – 3255,7/x

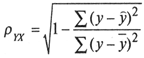
ρ_y,x = 0,858

Связь между показателем у и фактором х можно считать достаточно сильной.

Рассчитаем коэффициент детерминации R²

R² = ρ²_y,x

R² =0,736

Вариация результата Y (объема выпуска продукции) на 64 % объясняется вариацией фактора Х (объемом капиталовложений).

Рассчитаем F-критерий Фишера:

            R² *(n-2)

F_расч  =   1- R²

F_расч = 13,939

F_табл = 6,608 для ά=0,05; k₁=m=1;k₂=n-m-1=5

F_расч > F_табл

Уравнение регрессии с вероятностью 0.95 в целом статистически значимо т.к. F_расч > F_табл.

Определим среднюю относительную ошибку:             

Е_отн =  1/ n _*∑ | Ei/у|

Е_отн = 7,056

В среднем расчетные значения у_расч для гиперболической модели отличаются от фактических значений на 7,05%

Для выбора лучшей модели построим сводную таблицу результатов:

Модель Параметры	Коэффициент детерминации R2	F-критерий Фишера	Индекс корреляции r	Средняя относительная ошибка Еотн
Линейная	0,648	9,201	0,805	8,5
Степенная	0,64	8,886	0,8	8,095
Показательная	0,585	7,059	0,765	8,781

Все модели имеют примерно одинаковые но большее значение F-критерия Фишера и большее значение коэффициента детерминации R² имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза.

Расчет прогнозного значения результативного признака

5. Расчет прогнозного значения

Прогнозное значение результативного признака (объема выпуска продукции) определим по уравнению гиперболической модели подставив в него планируемую (заданную по условию)величину объема капитальных вложений:

х_пр = хср*1,1

х_пр = 85,01

у_пр = a+b/х_пр

у_пр = 50,30215

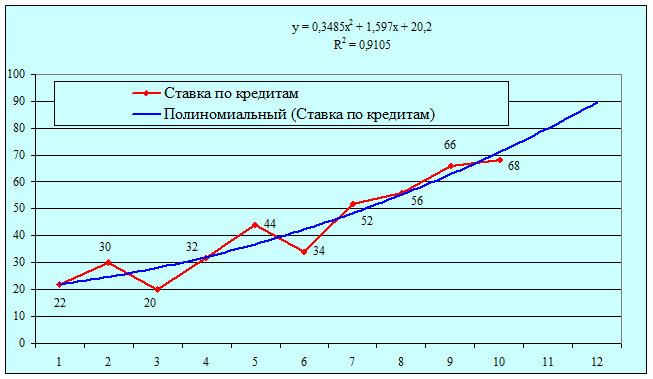
Фактические, расчетные и прогнозные значения по лучшей модели отобразим на графике.

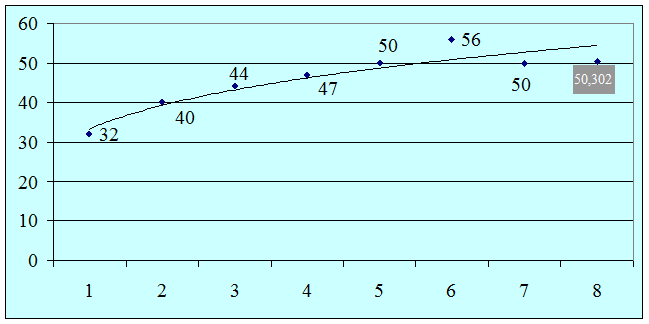Рис.1. Прогноз по лучшей модели

 

Задача  №2

 

По десяти кредитным учреждениям получены данные, ха­рактеризующие зависимость объема прибыли (Y) от среднегодо­вой ставки по кредитам (Х₁), ставки по депозитам (Х₂) и размера внутрибанковских расходов (Х₃).

Требуется:

1.                Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели.

2.                Рассчитать параметры модели.

3.                Для характеристики модели определить:

- линейный коэффициент множественной корреляции,

- коэффициент детерминации,

- средние коэффициенты эластичности,

- бетта-, дельта — коэффициенты. Дать их интерпретацию.

4.                Осуществить оценку надежности уравнения регрессии.

5.                Оценить с помощью t-критерия Стьюдента статистичес­кую значимость коэффициентов уравнения множествен­ной регрессии.

6.                Построить точечный и интервальный прогнозы результи­рующего показателя.

7.                Отразить результаты расчетов на графике.

Выполнение задач отразить в аналитической записке, при­ложить компьютерные распечатки расчетов.

Задание к задаче №2

Объем прибыли	Ставки по кредитам	Ставки по депозитам	Внутрибанковские расходы
Y	X1	X2	X3
50	22	176	150
54	30	170	154
60	20	156	146
62	32	172	134
70	44	162	132
54	34	160	126
84	52	166	134
82	56	156	126
86	66	152	88
84	68	138	120

n=10

m=3

1.                Выбор признаков для построения двухфакторной модели

С помощью MS Excel проведем корреляционный анализ

	Y	X1	X2	X3
Y	1
X1	0,924557	1
X2	-0,64459	-0,70453	1
X3	-0,70491	-0,79293	0,606154	1

Анализ матрицы коэффициентов парной корреляции показывает что Y имеет тесную связь со всеми факторами  но между факторами Х₁ и Х₃ связь теснее а значит можно говорить о мультиколлинеарности этих факторов поэтому мы выбираем фактор Х₂

2.                Выбор вида модели и оценка ее параметров

С помощью MS Excel проведем регрессионный анализ

                                                           4.5

Регрессионная статистика
Множественный R	0,925
R-квадрат	0,855
Нормированный R-квадрат	0,813
Стандартная ошибка	6,190
Наблюдения	10,000

Дисперсионный анализ				4.6
	df	SS	MS	F
Регрессия	2,000	1580,193	790,097	20,621
Остаток	7,000	268,207	38,315
Итого	9,000	1848,400

	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	33,295	47,311	0,704
X1	0,767	0,167	4,604
X2	0,017	0,261	0,066

ВЫВОД ОСТАТКА
		4.8
Наблюдение	Предсказанное Y	Остатки
1,000	53,220	-3,220
2,000	59,251	-5,251
3,000	51,340	8,660
4,000	60,819	1,181
5,000	69,848	0,152
6,000	62,145	-8,145
7,000	76,052	7,948
8,000	78,946	3,054
9,000	86,545	-0,545
10,000	87,835	-3,835

Уравнение регрессии зависимости объема прибыли от Ставки по кредитам и Ставки по депозитам можно записать в следующем виде:

у=33,295+0,767х₁+0,017х₂

3.                Оценка качества модели

В таблице 4.8 приведены вычисленные по модели значе­ния Y и значения остаточной компоненты.

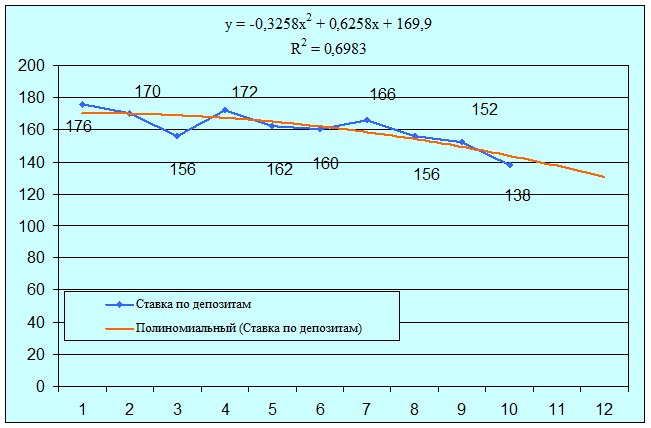
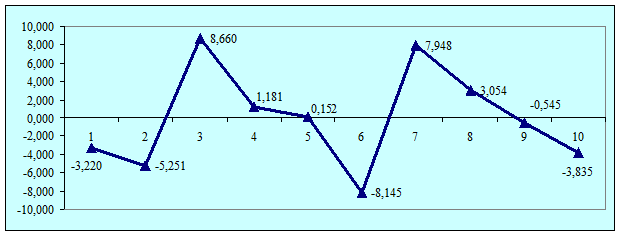Рис.2. График остатков

Вычислим для модели коэффициент детерминации.

Этот коэффициент уже вычислен нами и находится в таблице 4.5

R² = 0,855

Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обус­ловлено влиянием включенных факторов.

Проверку значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:

F_табл мы вычисляем с помощью функции FРАСПОБР

F_табл = 4,737

F_расч уже вычислено и находится в таблице 4.6

F_расч = 20,621

Поскольку .Р_расч > Р_табл, уравнение регрессии следует при­знать адекватным.

Учитывая, что коэффициент регрессии невозможно ис­пользовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, ис­пользуем коэффициент эластичности (Э) и бета-коэффициент, которые соответственно рассчитываются по формулам:

Эj = аj*x_{ср j} / y_ср

b = a_i * S_xi / S_y

	Промежуточные результаты при вычислении коэффициента эластичности и в-коэффициента
	у	х1	х2			х1		х2
	Объем реализации	Ставка по кредитам	Ставка по депозитам	уi-уср	(уi-уср)2	хi-хср	(хi-хср)2	хi-хср	(хi-хср)2
	50	22	176	-18,6	345,96	-20,4	416,16	15,2	231,04
	54	30	170	-14,6	213,16	-12,4	153,76	9,2	84,64
	60	20	156	-8,6	73,96	-22,4	501,76	-4,8	23,04
	62	32	172	-6,6	43,56	-10,4	108,16	11,2	125,44
	70	44	162	1,4	1,96	1,6	2,56	1,2	1,44
	54	34	160	-14,6	213,16	-8,4	70,56	-0,8	0,64
	84	52	166	15,4	237,16	9,6	92,16	5,2	27,04
	82	56	156	13,4	179,56	13,6	184,96	-4,8	23,04
	86	66	152	17,4	302,76	23,6	556,96	-8,8	77,44
	84	68	138	15,4	237,16	25,6	655,36	-22,8	519,84
Сумма	686	424	1608		1848,4		2742,4		1113,6
Сред.знач.	68,6	42,4	160,8

S2y	205,3778
S2x1	304,7111
S2x2	123,7333

Э₁ = 0,767*42,4/68,6 = 0,474

Э₂ = 0,017*160,8/68,6 = 0,040

b = 0,767 * 304,7111 / 205,3778 = 1,138

b = 0,017 * 123,7333 / 205,3778 = 0,010

Коэффициент эластичности показывает, на сколько про­центов изменяется зависимая переменная при изменении фак­тора на один процент.

Бета-коэффициент с математической точки зрения пока­зывает, на какую часть величины среднего квадратического от­клонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уров­не значении остальных независимых переменных.

4.                Оценка статистической значимости

Расчетные значения t-критерия Стьюдента для коэффици­ентов уравнения регрессии а,, а₂ приведены в четвертом столб­це таблицы 4.7

Табличное значение t-крите­рия Стьюдента можно найти с помощью функции СТЫОДРАСПОБР

t_табл=  2,36462256        

t_расч=0,704 

t_расч =4,604 критерий статистически значим

t_расч =0,066

        

5.                Точечный и интервальный прогноз