ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы
Автоматизированный
априорный анализ статистической совокупности в среде MS Excel.
Вариант
_113.
Выполнил:
ст. III курса гр ФиК
Проверил: Фагамов
УФА 2009
Постановка задачи.
При
проведении статистического наблюдения за деятельностью предприятий корпорации
получены выборочные данные о среднегодовой стоимости основных производственных
фондов и выпуске продукции за год по 32-м предприятиям, выпускающим однотипную
продукцию (выборка 10%-ная,
механическая).
В статистическом исследовании эти предприятия
выступают как единицы выборочной совокупности. Генеральную
совокупность образуют все предприятия корпорации.
Анализируемые признаки предприятий – Среднегодовая
стоимость основных производственных фондов и Выпуск продукции – изучаемые признаки единиц совокупности. Для
автоматизации статистических расчетов используются средства электронных таблиц
процессора Excel.
|
Исходные данные
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
94,00
|
110,00
|
|
2
|
107,00
|
101,00
|
|
3
|
134,00
|
120,00
|
|
4
|
157,00
|
81,00
|
|
5
|
163,00
|
80,00
|
|
6
|
167,00
|
114,00
|
|
7
|
173,00
|
161,00
|
|
8
|
173,00
|
90,00
|
|
9
|
177,00
|
178,00
|
|
10
|
179,00
|
107,00
|
|
11
|
200,00
|
125,00
|
|
12
|
201,00
|
108,00
|
|
13
|
205,00
|
133,00
|
|
14
|
208,00
|
124,00
|
|
15
|
212,00
|
201,00
|
|
16
|
213,00
|
161,00
|
|
17
|
214,00
|
151,00
|
|
18
|
216,00
|
169,00
|
|
19
|
218,00
|
149,00
|
|
20
|
230,00
|
180,00
|
|
21
|
234,00
|
148,00
|
|
22
|
237,00
|
162,00
|
|
23
|
241,00
|
166,00
|
|
24
|
248,00
|
168,00
|
|
25
|
45,00
|
224,00
|
|
26
|
276,00
|
171,00
|
|
27
|
290,00
|
191,00
|
|
28
|
298,00
|
220,00
|
|
29
|
167,00
|
114,00
|
|
30
|
205,00
|
133,00
|
|
31
|
330,00
|
53,00
|
|
32
|
260,00
|
224,00
|
I. Статистический анализ выборочной
совокупности
1.Выявить наличие среди
исходных данных резко выделяющихся значений признаков (выбросов данных) с целью
исключения из выборки аномальных единиц наблюдения.
2.Рассчитать обобщающие
статистические показатели совокупности по изучаемым признакам: среднюю
арифметическую (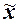 ), моду (Мо), медиану
(Ме),
размах вариации (R), дисперсию (
), моду (Мо), медиану
(Ме),
размах вариации (R), дисперсию (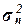 ), среднее отклонение
- линейное (
), среднее отклонение
- линейное (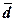 ) и квадратичное (
) и квадратичное (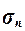 ), коэффициент вариации (Vσ),
структурный коэффициент ассиметрии К. Пирсона (Asп).
), коэффициент вариации (Vσ),
структурный коэффициент ассиметрии К. Пирсона (Asп).
3.На основе рассчитанных показателей в
предположении, что распределения единиц по обоим признакам близки к
нормальному, оценить:
а) степень колеблемости значений признаков в совокупности;
б) степень однородности
совокупности по изучаемым признакам;
в) устойчивость
индивидуальных значений признаков;
г) количество попаданий индивидуальных значений признаков в диапазоны
(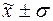 ), (
), (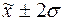 ), (
), ( ).
).
4.Дать сравнительную характеристику распределений
единиц совокупности по двум изучаемым признакам на основе анализа:
а) вариации признаков;
б) количественной
однородности единиц;
в) надежности (типичности)
средних значений признаков;
г) симметричности
распределений в центральной части ряда.
5.Построить интервальный вариационный ряд и
гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и
установить характер (тип) этого распределения.
II.
Статистический анализ генеральной
совокупности
1. Рассчитать генеральную
дисперсию 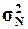 , генеральное среднее квадратическое отклонение
, генеральное среднее квадратическое отклонение 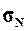 и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
2. Для изучаемых признаков
рассчитать:
а) среднюю ошибку выборки;
б) предельные ошибки выборки для уровней надежности
P=0,683, P=0,954, P=0,997 и границы, в которых будут находиться средние
значения признака генеральной совокупности при заданных уровнях надежности.
3. Рассчитать коэффициенты
асимметрии As
и эксцесса Ek.
На основе полученных оценок сделать
вывод об особенностях формы распределения единиц генеральной совокупности.
Выполнение статистических расчетов.
Задание
1.
Выявление и удаление
аномальных единиц наблюдения.
|
Исходные данные
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
94,00
|
110,00
|
|
2
|
107,00
|
101,00
|
|
3
|
134,00
|
120,00
|
|
4
|
157,00
|
81,00
|
|
5
|
163,00
|
80,00
|
|
6
|
167,00
|
114,00
|
|
7
|
173,00
|
161,00
|
|
8
|
173,00
|
90,00
|
|
9
|
177,00
|
178,00
|
|
10
|
179,00
|
107,00
|
|
11
|
200,00
|
125,00
|
|
12
|
201,00
|
108,00
|
|
13
|
205,00
|
133,00
|
|
14
|
208,00
|
124,00
|
|
15
|
212,00
|
201,00
|
|
16
|
213,00
|
161,00
|
|
17
|
214,00
|
151,00
|
|
18
|
216,00
|
169,00
|
|
19
|
218,00
|
149,00
|
|
20
|
230,00
|
180,00
|
|
21
|
234,00
|
148,00
|
|
22
|
237,00
|
162,00
|
|
23
|
241,00
|
166,00
|
|
24
|
248,00
|
168,00
|
|
25
|
45,00
|
224,00
|
|
26
|
276,00
|
171,00
|
|
27
|
290,00
|
191,00
|
|
28
|
298,00
|
220,00
|
|
29
|
167,00
|
114,00
|
|
30
|
205,00
|
133,00
|
|
31
|
330,00
|
53,00
|
|
32
|
260,00
|
224,00
|
Таблица 1
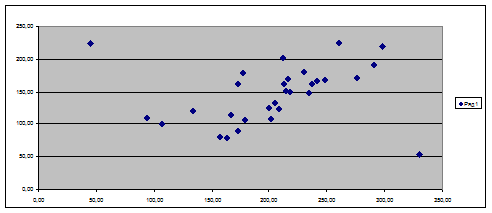
Рис.1 Аномальные значения признаков на диаграмме
рассеивания
Аномальные
единицы наблюдения
|
Номер предприятия
|
Среднегодовая
стоимость основных
|
Выпуск
продукции, млн.руб
|
|
|
производственных
фондов, млн.руб
|
|
|
|
25
|
45
|
|
224
|
|
|
31
|
330
|
|
53
|
|
Таблица
2
Задание
2.
Оценка описательных
статистических параметров совокупности
|
Описательные статистики
|
|
По столбцу "Среднегодовая стоимость основных
производственных фондов, млн.руб."
|
По столбцу "Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
Среднее
|
203,2333333
|
Среднее
|
144,6666667
|
|
Стандартная ошибка
|
8,804737927
|
Стандартная ошибка
|
7,071772174
|
|
Медиана
|
206,5
|
Медиана
|
148,5
|
|
Мода
|
167
|
Мода
|
114
|
|
Стандартное отклонение
|
48,22553575
|
Стандартное отклонение
|
38,73369141
|
|
Дисперсия выборки
|
2325,702299
|
Дисперсия выборки
|
1500,298851
|
|
Эксцесс
|
0,18281271
|
Эксцесс
|
-0,602481285
|
|
Асимметричность
|
-0,185105228
|
Асимметричность
|
0,218561586
|
|
Интервал
|
204
|
Интервал
|
144
|
|
Минимум
|
94
|
Минимум
|
80
|
|
Максимум
|
298
|
Максимум
|
224
|
|
Сумма
|
6097
|
Сумма
|
4340
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень надежности(95,4%)
|
18,35621488
|
Уровень надежности(95,4%)
|
14,74330874
|
Таблица
3
|
Предельные ошибки
выборки
|
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск
продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
8,965035119
|
Уровень
надежности(68,3%)
|
7,200519359
|
Таблица 4а
|
Предельные ошибки выборки
|
|
По столбцу "Среднегодовая стоимость основных
производственных фондов, млн.руб."
|
По столбцу "Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
Уровень надежности(99,7%)
|
28,52215671
|
Уровень надежности(99,7%)
|
22,90837
|
|
|
|
|
Таблица 4в
|
Выборочные показатели вариации и асимметрии
|
|
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск
продукции, млн.руб"
|
|
Стандартное
отклонение
|
47,41496482
|
Стандартное
отклонение
|
326,2391884
|
|
Дисперсия
|
2248,178889
|
Дисперсия
|
106432,0081
|
|
Среднее
линейное отклонение
|
36,66888889
|
Среднее
линейное отклонение
|
251,3133333
|
|
Коэффициент
вариации, %
|
23,33030908
|
Коэффициент
вариации, %
|
225,5109597
|
|
Коэффициент
асимметрии Asп
|
0,764175055
|
Коэффициент
асимметрии Asп
|
0,805265907
|
Таблица 5
Задание 3
Построение и графическое
изображение интервального вариационного ряда распределения единиц совокупности по
признаку Среднегодовая стоимость основных производственных фондов
|
Карман
|
Частота
|
Карман
|
Частота
|
|
94
|
1
|
|
|
|
134,8
|
2
|
134,8
|
3
|
|
175,6
|
6
|
175,6
|
6
|
|
216,4
|
11
|
216,4
|
11
|
|
257,2
|
6
|
257,2
|
6
|
|
еще
|
4
|
298
|
4
|
Таблица 6
|
Интервальный ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
Группа предприятий по стоимости основных фондов
|
Число предприятий в группе
|
Накопленная частость группы.%
|
|
94-134,8
|
3
|
10,00%
|
|
134,8-175,6
|
6
|
30,00%
|
|
175,6-216,4
|
11
|
66,67%
|
|
216,4-257,2
|
6
|
86,67%
|
|
257,2-298
|
4
|
100,00%
|
|
Итого
|
30
|
|
Таблица 7
Гистограмма
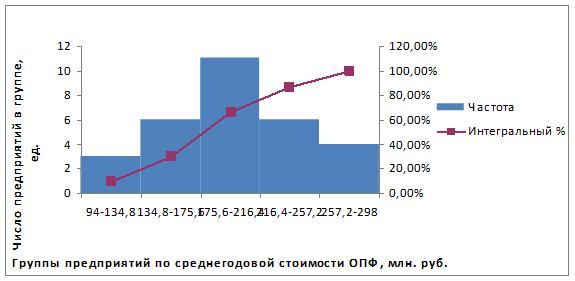
Рис.2 Столбиковая диаграмма и кумулята
3. Выводы по результатам выполнения лабораторной работы
I. Статистический анализ выборочной совокупности
Задача 1. Указать количество
аномальных единиц наблюдения равно двум, со ссылкой на табл.2.
Задача 2. Рассчитанные
выборочные показатели представлены в двух таблицах - табл.3 и табл.5. На основе
этих таблиц формируется единая таблица (табл.8) значений
выборочных показателей, перечисленных в условии Задачи 2.
Таблица 8
Описательные статистики
выборочной совокупности
|
Обобщающие статистические показатели совокупности по
изучаемым признакам
|
Признаки
|
|
Среднегодовая
стоимость основных производственных фондов
|
Выпуск продукции
|
|
Средняя арифметическая (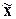 ) )
|
203,23
|
144,67
|
|
Мода (Мо)
|
167,00
|
114,00
|
|
Медиана (Ме)
|
206,50
|
148,50
|
|
Размах вариации(R)
|
204,00
|
144,00
|
|
Дисперсия(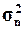 ) )
|
2248,18
|
1450,29
|
|
Среднее линейное отклонение (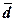 ) )
|
36,67
|
32,36
|
|
Среднее квадратическое
отклонение (σn)
|
47,41
|
38,08
|
|
Коэффициент вариации (Vσ)
|
23,33
|
26,32
|
|
Коэффициент асимметрии К.Пирсона (Asп)
|
0,76
|
0,18
|
Задача 3.
3а). Степень колеблемости признака определяется
по значению коэффициента вариации Vs в соответствии с оценочной шкалой
колеблемости признака.
0%<Vs≤40% - колебаемость незначительна
40%<Vs≤60% - колебаемость
средняя (умеренная)
Vs >60% - колебаемость
значительная
Вывод: Для признака Среднегодовая стоимость основных
производственных фондов показатель Vs = 23,33
Для признака Выпуск продукции показатель Vs = 26,32
коэффициенты вариации Vs =и Vs =попадают
в диапазоне 0%<Vs≤40% - колеблемость признаков незначительная.
3б). Однородность совокупности по
изучаемому признаку для нормального и близких к нормальному распределений
устанавливается по значению коэффициента вариации Vs. Если
его значение невелико (Vs<33%), то индивидуальные значения признака xi мало отличаются друг от друга, единицы наблюдения
количественно однородны.
Вывод: Для признака Среднегодовая стоимость основных
производственных фондов показатель Vs < 33%, следовательно, по данному признаку выборочная совокупность б является
однородной.
3в). Сопоставление средних
отклонений – квадратического s и
линейного 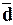 позволяет
сделать вывод об устойчивости
индивидуальных значений признака, т.е.
об отсутствии среди них «аномальных» вариантов значений.
позволяет
сделать вывод об устойчивости
индивидуальных значений признака, т.е.
об отсутствии среди них «аномальных» вариантов значений.
В условиях симметричного и
нормального, а также близких к ним распределений между показателями s и 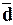 имеют место
равенства s
имеют место
равенства s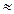 1,25
1,25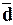 ,
,
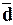
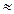 0,8s, поэтому отношение
показателей
0,8s, поэтому отношение
показателей 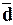 и s может
служить индикатором устойчивости данных.
и s может
служить индикатором устойчивости данных.
Если 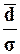 >0,8, то
значения признака неустойчивы, в них имеются «аномальные» выбросы.
Следовательно, несмотря на визуальное обнаружение и исключение нетипичных
единиц наблюдений при выполнении Задания 1, некоторые аномалии в первичных
данных продолжают сохраняться. В этом случае их следует выявить (например,
путем поиска значений, выходящих за границы (
>0,8, то
значения признака неустойчивы, в них имеются «аномальные» выбросы.
Следовательно, несмотря на визуальное обнаружение и исключение нетипичных
единиц наблюдений при выполнении Задания 1, некоторые аномалии в первичных
данных продолжают сохраняться. В этом случае их следует выявить (например,
путем поиска значений, выходящих за границы (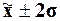 )) и
рассматривать в качестве возможных «кандидатов» на исключение из выборки.
)) и
рассматривать в качестве возможных «кандидатов» на исключение из выборки.
Для признака Среднегодовая стоимость основных
производственных фондов показатель 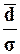 = 0,77<0.8 следовательно, значения признака
устойчивы.
= 0,77<0.8 следовательно, значения признака
устойчивы.
Для признака Выпуск продукции показатель 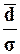 =0,85 что незначительно отклоняется от 0,8. Следовательно,
значения признака не устойчивы, в них имеются «аномальные» выбросы. В качестве
возможных кандидатов на исключение из
выборки могут быть значения выходящие за границы диапазона ( ) – это значение
выпуска продукции 224.
=0,85 что незначительно отклоняется от 0,8. Следовательно,
значения признака не устойчивы, в них имеются «аномальные» выбросы. В качестве
возможных кандидатов на исключение из
выборки могут быть значения выходящие за границы диапазона ( ) – это значение
выпуска продукции 224.
3г). Для оценки количества
попаданий индивидуальных значений признаков xi в тот или иной диапазон отклонения от средней 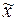 , а также для установления процентного соотношения
рассеяния значений xi по 3-м диапазонам формируется табл.9 (с конкретными числовыми значениями
границ диапазонов)
, а также для установления процентного соотношения
рассеяния значений xi по 3-м диапазонам формируется табл.9 (с конкретными числовыми значениями
границ диапазонов)
Таблица 9
|
Границы
диапазонов
|
Количество
значений xi,
находящихся в диапазоне
|
Процентное
соотношение рассеяния значений xi по диапазонам, %
|
|
А
|
Первый
признак
|
Второй
признак
|
Первый
признак
|
Второй
признак
|
Первый
признак
|
Второй
признак
|
|
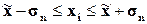
|
[155,82;250,65]
|
[106,58;182,75]
|
23
|
22
|
76,67
|
73,33
|
|

|
[108,40;298,06]
|
[68,50;220,83]
|
28
|
29
|
93,3
|
96,67
|
|
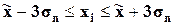
|
[60,99;313,24]
|
[30,42;241,73]
|
30
|
30
|
100
|
100
|
Распределение значений
признака по диапазонам рассеяния признак относительно 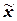
На основе данных табл.9
процентное соотношение рассеяния значений признака по трем диапазонам
сопоставляется с рассеянием по правилу «трех сигм», справедливому для
нормальных и близких к нему распределений:
68,3% значений располагаются
в диапазоне (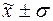 ),
),
95,4% значений располагаются
в диапазоне (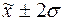 ),
),
99,7% значений располагаются
в диапазоне (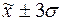 ).
).
Если полученное в табл. 9
процентное соотношение рассеяния хi по 3-м диапазонам незначительно расходится с правилом
«3-х сигм», можно предположить, что изучаемое распределение признака близко к
нормальному.
Расхождение с правилом «3-х
сигм» может быть существенным.
Например, менее 60% значений
хi попадают в центральный
диапазон (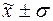 ) или значительно более 5% значения хi выходит за диапазон (
) или значительно более 5% значения хi выходит за диапазон (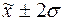 ). В этих случаях распределение нельзя считать близким
к нормальному.
). В этих случаях распределение нельзя считать близким
к нормальному.
Вывод: Сравнение данных
графы 5 табл. 9 с правилом «3-х сигм» показывает на их незначительное
расхождение, следовательно,
распределение единиц совокупности
по признаку Среднегодовая стоимость основных производственных фондов можно
считать близким к нормальному.
Сравнение данных графы 6
табл. 9 с правилом «3-х сигм» показывает на их незначительное расхождение, следовательно, распределение единиц совокупности по признаку Выпуск продукции
можно считать близким к нормальному.
Вывод: полученное в табл. 9
процентное соотношение рассеяния хi по 3-м диапазонам незначительно расходится с
правилом «3-х сигм», можно предположить, что изучаемое распределение признака
близко к нормальному.
Задача 4. Для ответа на
вопросы 4а) – 4г) необходимо воспользоваться табл.8 и сравнить величины показателей для двух признаков.
4а). Размах
вариации , которой мы находим по формуле: R = Xmax – Xmin,
устанавливает предельное значение амплитуды колебаний признака. Его значение
больше у второго признака, амплитуда шире.
О большой колеблимости
второго признака свидетельствует большой показатель среднего линейного
отклонения (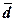 ) 174,83 против 153,07 а так же среднее квадратичное
отклонение (σn)230,83
против 193,0.
) 174,83 против 153,07 а так же среднее квадратичное
отклонение (σn)230,83
против 193,0.
4б). Сравнение
количественной однородности единиц.
Чем меньше значение
коэффициента вариации Vs, тем более
однородна совокупность.
Вывод: Для признака среднегодовая стоимость основных
производственных фондов Vs = 23,33% а для признака выпуск продукции Vs = 26,32.
Так как коэффициент вариации Vs для первого признака меньше чем коэффициент для
второго признака, то однородность совокупности
значений признака Среднегодовая стоимость основных производственных
фондов более однородна, чем совокупность значений признака Выпуск продукции.
4в). Сравнение
надежности (типичности) средних значений признаков.
Чем
более однородна совокупность, тем надежнее среднее значение признака 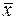
Вывод: т.к. единицы наблюдения количественно однородны , следовательно средняя
арифметическая величина 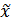 является надежной
характеристикой данной совокупности.
является надежной
характеристикой данной совокупности.
4г). Сравнение
симметричности распределений в центральной части ряда.
В нормальных и близких к
нему распределениях основная масса единиц (63,8%) располагается в центральной
части ряда, в диапазоне (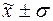 ). Для оценки асимметрии распределения в этом центральном
диапазоне служит коэффициент К.Пирсона – Asп.
). Для оценки асимметрии распределения в этом центральном
диапазоне служит коэффициент К.Пирсона – Asп.
При правосторонней
асимметрии Asп>0,
при левосторонней – Asп<0.
Если Asп=0,
вариационный ряд симметричен.
Вывод: Асимметрия распределения признака Среднегодовая стоимость основных производственных фондов в
центральной части ряда является правосторонней, так как Asп=0,76.
Асимметрия признака Выпуск продукции является
правосторонней, так как Asп=0,81. Сравнение абсолютных величин |Аsп| для
обоих рядов показывает, что ряд распределения признака Среднегодовая стоимость основных производственных фондов менее
асимметричен, чем ряд распределения признака Выпуск продукции.
Задача 5. Интервальный вариационный ряд
распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов
представлен в табл.7, а гистограмма и кумулята – на
рис.2. Возможность отнесения
распределения признака «Среднегодовая
стоимость основных производственных фондов» к семейству нормальных
распределений устанавливается путем анализа формы гистограммы распределения.
Анализируется количество вершин в гистограмме, ее асимметричность и
выраженность «хвостов», т.е. частоты появления в распределении значений,
выходящих за диапазон (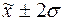 ).
).
Если гистограмма имеет одновершинную форму, есть основания
предполагать, что выборочная совокупность может иметь характер распределения,
близкий к нормальному.
Для дальнейшего анализа формы распределения используются описательные
параметры выборки - показатели центра распределения (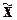 , Mo,
Me),
вариации (
, Mo,
Me),
вариации (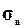 ),
асимметрии в центральной части
распределения (AsП). Совокупность этих показателей позволяет дать качественную оценку
близости эмпирических данных к нормальной форме распределения.
),
асимметрии в центральной части
распределения (AsП). Совокупность этих показателей позволяет дать качественную оценку
близости эмпирических данных к нормальной форме распределения.
Нормальное распределение
является симметричным, и для него выполняется соотношения:
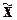 =Mo=Me, Asп=0, Rn=6sn.
=Mo=Me, Asп=0, Rn=6sn.
Нарушение этих соотношений свидетельствует о наличии
асимметрии распределения. Распределение с небольшой или умеренной асимметрией в
большинстве случаев относятся к нормальному типу.
По признаку Среднегодовая стоимость
основных производственных фондов 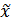 = 202,23, Mо
=167, Ме =206,5,
= 202,23, Mо
=167, Ме =206,5, 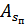 =0,76,
=0,76, 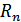 =204, 6σn
= 6*47,41=284,49. Распределение можно отнести к нормальному.
=204, 6σn
= 6*47,41=284,49. Распределение можно отнести к нормальному.
3. В нормальном и близким к
нему распределениях крайние варианты значения признака (близкие к хmin и хmax) встречаются много реже (5-7 % всех случаев), чем
серединные (лежащие в диапазоне (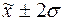 )).
Следовательно, по проценту выхода значений признака за пределы диапазона (
)).
Следовательно, по проценту выхода значений признака за пределы диапазона (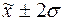 )
можно судить о соответствии длины «хвостов» распределения нормальному закону.
)
можно судить о соответствии длины «хвостов» распределения нормальному закону.
«Хвосты»
распределения соответствуют нормальному закону.
II.
Статистический анализ генеральной
совокупности
Задача 1. Рассчитанные
генеральные показатели представлены в табл.10.
|
Обобщающие статистические
показатели совокупности по изучаемым признакам
|
Признаки
|
|
Среднегодовая стоимость основных производственных фондов
|
Выпуск продукции
|
|
Стандартное отклонение 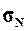
|
47,41
|
38,08
|
|
Дисперсия 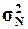
|
2248,18
|
1450,29
|
|
Асимметричность As
|
-0,19
|
0,22
|
|
Эксцесс
Ek
|
0,18
|
-0,60
|
Таблица 10
Описательные статистики
генеральной совокупности
Установим степень схожести между 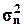 и
и 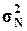 .
.
Используем формулу 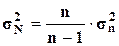 .
.
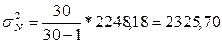 - для среднегодовой стоимости ОПФ
- для среднегодовой стоимости ОПФ
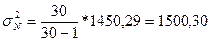 - для выпуска продукции
- для выпуска продукции
Рассчитаем
отношение 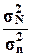 для двух признаков:
для двух признаков:
Для первого
признака 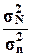 =1,03448, расхождение незначительное.
=1,03448, расхождение незначительное.
И для второго признака 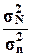 =1,03448,
расхождение незначительное.
=1,03448,
расхождение незначительное.
Для нормального
распределения справедливо равенство RN=6sN.
В условиях
близости распределения единиц генеральной совокупности к нормальному это
соотношение используется для прогнозной оценки размаха вариации признака в
генеральной совокупности.
Величина расхождения между показателями
RN и Rn:
- для первого
признака |RN -Rn|=
284,49 – 204,0= 80,49
- для второго
признака |RN -Rn| = 228,50 - 144,0= 84,50
Применение
выборочного метода наблюдения связано с измерением степени достоверности
статистических характеристик генеральной совокупности, полученных по
результатам выборочного наблюдения. Достоверность генеральных параметров
зависит от репрезентативности выборки,
т.е. от того, насколько полно и адекватно представлены в выборке статистические
свойства генеральной совокупности.
Как правило, статистические
характеристики выборочной и генеральной совокупностей не совпадают, а
отклоняются на некоторую величину ε, которую называют ошибкой
выборки (ошибкой репрезентативности).
Ошибка выборки – это разность между значением показателя, который был получен
по выборке, и генеральным значением этого показателя. Например, разность
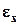 =
|
=
|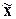 -
-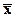 |
|
определяет ошибку
репрезентативности для средней величины признака.
Для среднего значения
признака средняя ошибка выборки 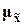 (ее
называют также стандартной ошибкой)
выражает среднее квадратическое отклонение s выборочной
средней
(ее
называют также стандартной ошибкой)
выражает среднее квадратическое отклонение s выборочной
средней 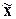 от
математического ожидания M[
от
математического ожидания M[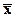 ] генеральной средней
] генеральной средней 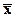 .
.
Предельная ошибка выборки 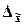 определяет границы, в пределах
которых лежит генеральная средняя
определяет границы, в пределах
которых лежит генеральная средняя 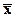 . Эти границы задают так называемый доверительный интервал генеральной средней
. Эти границы задают так называемый доверительный интервал генеральной средней 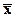 – случайную
область значений, которая с вероятностью P,
близкой к 1, гарантированно содержит значение
генеральной средней. Эту вероятность называют доверительной вероятностью или уровнем
надежности.
– случайную
область значений, которая с вероятностью P,
близкой к 1, гарантированно содержит значение
генеральной средней. Эту вероятность называют доверительной вероятностью или уровнем
надежности.
Для уровней надежности P=0,954; P=0,997; P=0,683 оценки
предельных ошибок выборки 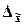 даны в табл. 3, табл. 4а и табл. 4б.
даны в табл. 3, табл. 4а и табл. 4б.
Для генеральной средней
предельные значения и доверительные интервалы определяются выражениями:
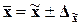 ,
,
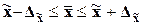
Предельные ошибки выборки и
ожидаемые границы для генеральных средних представлены в табл. 11.
Предельные ошибки выборки и
ожидаемые границы для генеральных средних
|
Доверительная
вероятность
Р
|
Коэффициент
доверия
t
|
Предельные ошибки выборки
|
Ожидаемые границы для средних 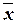
|
|
для первого
признака
|
для второго
признака
|
для первого
признака
|
для второго
признака
|
|
0,683
|
1
|
8,96
|
7,20
|
194,27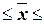 212,19 212,19
|
173,47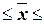 151,87 151,87
|
|
0,954
|
2
|
18,36
|
14,74
|
184,87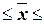 221,59 221,59
|
129,93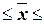 159,41 159,41
|
|
0,997
|
3
|
28,52
|
22,91
|
174,71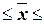 231,75 231,75
|
121,76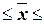 167,58 167,58
|
Вывод: Увеличение уровня надежности ведет к расширению
ожидаемых границ для генеральных средних.
Задача 3 Значения коэффициентов асимметрии As и эксцесса Ek
даны в табл.10.
Показатель асимметрии As оценивает смещение ряда распределения влево или
вправо по отношению к оси симметрии нормального распределения.
Если асимметрия правосторонняя (As>0) то правая часть эмпирической кривой оказывается
длиннее левой, т.е. имеет место неравенство 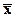 >Me>Mo, что означает преимущественное
появление в распределении более высоких значений признака. (среднее значение
>Me>Mo, что означает преимущественное
появление в распределении более высоких значений признака. (среднее значение 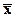 больше
серединного Me
и модального Mo).
больше
серединного Me
и модального Mo).
Если асимметрия левосторонняя (As<0), то левая часть эмпирической кривой оказывается
длиннее правой и выполняется неравенство 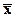 <Me<Mo, означающее, что в распределении чаще встречаются более низкие значения признака (среднее значение
<Me<Mo, означающее, что в распределении чаще встречаются более низкие значения признака (среднее значение 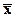 меньше
серединного Me
и модального Mo).
меньше
серединного Me
и модального Mo).
Чем больше величина |As|, тем более
асимметрично распределение. Оценочная шкала асимметрии:
|As|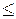 0,25 - асимметрия незначительная;
0,25 - асимметрия незначительная;
0,25<|As|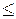 0.5 -
асимметрия заметная (умеренная);
0.5 -
асимметрия заметная (умеренная);
|As|>0,5 -
асимметрия существенная.
Вывод: Для признака Среднегодовая
стоимость основных производственных фондов наблюдается незначительная
левосторонняя асимметрия.
Показатель эксцесса Ek характеризует крутизну
кривой распределения - ее заостренность или пологость по сравнению с нормальной
кривой.
Если Ek>0, то вершина кривой
распределения располагается выше вершины
нормальной кривой, а форма кривой является более островершинной, чем
нормальная. Это говорит о скоплении значений признака в центральной зоне ряда
распределения, т.е. о преимущественном
появлении в данных значений, близких к средней величине.
Если Ek<0, то вершина кривой
распределения лежит ниже вершины нормальной кривой, а форма кривой более
пологая по сравнению с нормальной. Это означает, что значения признака не
концентрируются в центральной части ряда, а достаточно равномерно рассеяны по
всему диапазону от xmax до xmin.
Для нормального
распределения Ek=0. При
незначительном отклонении Ek от нуля форма кривой эмпирического распределения
незначительно отличается от формы нормального распределения. Чем больше абсолютная величина |Ek|, тем существеннее распределение отличается
от нормального.
Вывод:
1. Для признака Среднегодовая стоимость основных
производственных фондов Ek<0, что свидетельствует о том,
что вершина кривой распределена, лежит ниже вершины нормальной кривой, а форма
кривой более пологая по сравнению с нормальной кривой. При этом Ek незначительно отличается от нуля. Следовательно, по
данному признаку форма кривой эмпирического распределения незначительно
отличается от формы нормального распределения.
2. Для признака Выпуск продукции Ek<0, что свидетельствует о том,
что вершина кривой распределения лежит ниже вершины нормальной кривой, а форма
кривой более пологая по сравнению с нормальной кривой. При этом Ek незначительно отличается от нуля. Следовательно, по
данному признаку форма кривой эмпирического распределения незначительно
отличается от формы нормального распределения.
III.
Экономическая интерпретация результатов статистического исследования
предприятий.
Задача 1.
образующие выборку предприятия типичны по значениям
изучаемых экономических показателей, но присутствуют 2 аномальных единицы
наблюдения которые были исключены из выборки.
Задача 2.
В экономических характеристиках предприятий выборочной
совокупности нет больших различий, выборка сформирована из предпиятий с
достаточно близкими значениями по каждому из показателей.
Задача 3.
Коэффициент вариации
показывает что для двух изучаемых признаков колебамоемость
вариантов относительно средней величины незначительная ( т.к. не превышает 40%).
Следовательно, различия в экономических характеристиках
предприятий выборочной совокупности не сильны и выборка сформирована из
предприятий с достаточно близкими значениями по каждому из показателей.
Задача 4.
Структура предприятий
выборочной совокупности по среднегодовой стоимости основных фондов представлена
в табл. №9. Удельный вес предприятий с наибольшими значениями данного
показателя – 100%, наименьшими – 76,67% и типичными – 93,33%.
Задача 5.
Распределение предприятий по
группам носит закономерный характер. В совокупности преобладают
предприятия со стоимостью основных
фондов в пределах от 175,6 до 216,4 млн. руб.: 11 предприятий из 30.
Задача 6.
Ожидаемые средние величины
на предприятиях корпорации в целом: среднегодовой стоимости основных фондов =
203,23, выпуска продукции = 144,67. Максимальное расхождение в значениях
показателя по первому признаку : 48,23, по второму: 38,73. Границы, в которых
будут находятся средние значения показателей, представлены в табл. 11.