Исходные данные

Пусть некоторое производственное предприятие за 2003 отчетный год имело следующие показатели эффективности производства.

Таблица 1

Номер объекта	Y3	X6	X7	X9	X12
1	13,26	0,23	1,45	167,69	166,32
2	10,16	0,39	1,30	186,10	92,88
3	13,72	0,43	1,37	220,45	158,04
4	12,85	0,18	1,65	169,30	93,96
5	10,63	0,15	1,91	39,53	173,88
6	9,12	0,34	1,68	40,41	162,30
7	25,83	0,38	1,94	102,96	88,56
8	23,39	0,09	1,89	37,02	101,16
9	14,68	0,14	1,94	45,74	166,32
10	10,05	0,21	2,06	40,07	140,76
11	13,39	0,42	1,96	45,44	128,52
12	9,68	0,05	1,02	41,08	177,84
13	10,03	0,29	1,85	136,14	114,48
14	9,13	0,48	0,88	42,39	93,24
15	5,37	0,41	0,62	37,39	126,72
16	9,86	0,62	1,09	101,78	91,80
17	12,62	0,56	1,60	47,55	69,12
18	5,02	1,76	1,52	32,61	66,24
19	21,18	1,31	1,40	103,25	67,68
20	25,17	0,45	2,22	38,95	50,40

Где  Y₃ – рентабельность производства,

X₆ – удельный вес потерь от брака,

X₇ – уровень фондоотдачи,

X₉ – среднегодовая стоимость основных производственных фондов,

X₁₂ – коэффициент оборачиваемости нормируемых оборотных средств.

Необходимо исследовать взаимосвязи данных показателей с помощью: многомерного корреляционного и регрессионного анализа, факторного анализа, компонентного анализа и дискриминантного анализа.

Многомерный корреляционный и регрессионный анализ

Корреляционный анализ, разработанный К.Пирсоном и Дж.Юлом, является одним из методов статистического анализа взаимозависимости нескольких признаков - компонент случайного вектора х.

Одним из основных показателей взаимозависимости двух случайных величин является парный коэффициент корреляции, служащий мерой линейной статистической зависимости между этими величинами. То же самое касается частных и сово­купных коэффициентов корреляции. Одним из требований, определяю­щих корреляционный метод, является требование линейности статисти­ческой связи, т.е. линейности всевозможных уравнений (средней квадратической) регрессии.

В настоящее время корреляционный анализ (корреляционная модель) определяется как метод, применяемый тогда, когда данные наблюдений или эксперимента можно считать случайными и выбранными из гене­ральной совокупности, распределенной по многомерному нормальному закону.

Основная задача корреляционного анализа состоит в оценке k(k+3)/ 2 параметров, определяющих нормальный закон распределения к-мерного вектора х, в частности, корреляционной матрицы генеральной совокуп­ности X, по выборке.

После того как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показа­тель у и аргументы Х1,X2,...,Xk, отбирают наиболее информативные аргу­менты, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют точность полученного уравнения.

Функция f{Х1,Х2,...,Хk), описывающая зависимость условного среднего значения результативного признака у от заданных значений аргументов, называется функцией (уравнением) регрессии.

Для выяснения "чистых", истинных взаимозависимостей следует про­анализировать выборочные частные коэффициенты корреляции (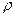). Рассмотрим частные коэффициенты корреляции показателя рентабельности производства с удельным весом потерь от брака, уровнем фондоотдачи, среднегодовой стоимостью основных производственных фондов, коэффициентом оборачиваемости нормируемых оборотных средств.

Для этого в EXCEL рассчитаем матрицу корреляций.

	Y3	X6	X7	X9	X12
Y3	1
X6	-0,10948	1
X7	0,531274	-0,17152	1
X9	0,05458	-0,07479	-0,13231	1
X12	-0,34129	-0,57765	-0,04563	0,029309	1

По шкале Чеддока характеристика силы связи между Y3 и Х6 слабая, между   Y3 и Х7 заметная,  между Y3 и Х9 очень слабая, между Y3 и Х12 умеренная.

Проверим значимость полученных параметров связи по t-критерию Стьюдента. Для этого рассчитаем t-статистики для каждого из коэффициентов корреляции Y3 и Хi по формуле:

 

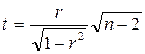
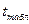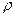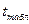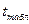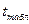Сравним полученное значение с табличным значение t-статистики Стьюдента с n-2 степенями свободы с 5% уровнем значимости (). Для проверки гипотезы Н₀: =0, сравниваем |t_расч| и . Если |t_расч| >, то гипотеза Н₀ отвергается с вероятностью ошибки 5%, если |t_расч| < , то гипотеза не отвергается.

Значения  tрасч для коэффициентов корреляции Y3 с Хi
	tрасч	|tрасч|
X6	-0,470125	0,470125
X7	3,140385	3,140385
X9	0,232256	0,232256
X12	-1,63886	1,63886

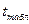=1,101      для распределения Стьюдента с 18 степенями свободы и 5% уровнем значимости.

Значимыми по критерию Стьюдента являются связи между Y3 и Х7, и Y3 и Х12.

Проведем корреляционный анализ генеральной совокупности трех признаков Y3, Х7 и Х12.

Точечные оценки девяти генеральных параметров (среднего, дисперсии и корреляции) можно вычислить в EXCEL.

Y3		X7		X12
Среднее	13,257	Среднее	1,5675	Среднее	116,51
Дисперсия выборки	36,527	Дисперсия выборки	0,1829	Дисперсия выборки	1654,8

	Y3	X6	X7	X9	X12
Y3	1
X6	-0,10948	1
X7	0,531274	-0,17152	1
X9	0,05458	-0,07479	-0,13231	1
X12	-0,34129	-0,57765	-0,04563	0,029309	1

 ,,

,,

, , .

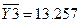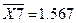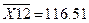
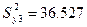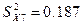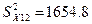
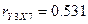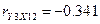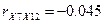Далее вычислим оценки условных средних квадратических отклонений при фиксировании одной переменной:

.

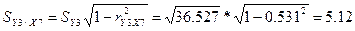
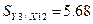
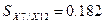
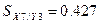
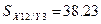
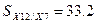Найдем точечные оценки частных коэффициентов корреляции:

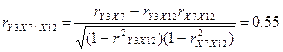
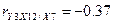
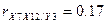
Вычислим точечные оценки остаточных дисперсий (при фиксировании двух переменных):

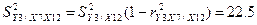
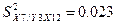
Получаем оценки множественных коэффициентов детерминации и корреляции:

  

   

   

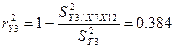
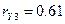
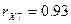
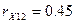
Проверим с уровнем  5% значимость множественных коэффициентов  детерминации. Вычислим наблюдаемые значения F-критерия:

 

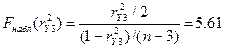
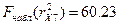
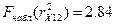
Находим, по таблице F-распределения критическое значение F-статистики для уровня значимости 5%, числа степеней свободы числителя 2 и знаменателя 20-3=17:

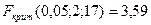
Так как наблюдаемые значения F-статистик для 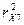 и 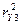 превосходят ее критическое значение то с вероятностью ошибки 5% отвергается гипотеза об отсутствии связи между случайной величиной Y3 и (Х7, Х12), и между Х7 и (Y3, Х12).  Так как коэффициент 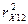 не значим, то связь между X12 и (Y3, Х7) отсутствует.

На основании полученных расчетов по трехмерной модели (Y3,Х7,Х12)  можно сделать следующие выводы.

Доказана тесная взаимосвязь между уровнем фондоотдачи и двумя остальными показателями - уровнем рентабельности производства и коэффициентом оборачиваемости нормируемых оборотных средств (множественный коэффициент детерминации значим и превышает 0,8). Изменение фондоотдачи в среднем на 87% объясняется изменением рентабельности и коэффициента оборачиваемости. Взаимозависимость коэффициента оборачиваемости и уровня фондоотдачи (без учета уровня рентабельности) не доказана (частный коэффициент корреляции незначим) при данных условиях. 

После того как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты, перейдем к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа.

Построим уравнение множественной линейной регрессии:

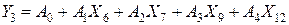
Используем автоматизированное вычисление множественного линейного уравнения связи (регрессии)  с помощью EXCEL.

	Коэффициенты	Стандартная ошибка
А0	12,70367	7,962561
А1	-4,58609	3,545411
А2	6,631436	2,797818
А3	0,01078	0,019186
А4	-0,07472	0,035112

Получаем уравнение множественной связи:

Y₃= 12.7 – 4.586X₆+6.63X₇+0.01X₉-0.074X₁₂

Из уравнения видно, что основным признаком, определяющим снижение уровня  рентабельности является удельный вес потерь от брака. Наиболее заметным фактором повышения рентабельности является уровеь фондоотдачи.

Значимость уравнения регрессии в целом оценивается посредством F-критерия. Рассчитывается величина F-статистики, которая сравнивается с табличным значением при соответствующих показателях числа степеней свободы и уровня значимости (как единица минус уровень доверительной вероятности).

Составим расчетную таблицу для удобства вычислений.

	df- число степеней свободы	Сумма квадратов отклонений (SS)	MS=SS/df	F-расчетное
Регрессия	4	319,8865	79,97161	3,206399
Остаток	15	374,1188	24,94125
Итого	19	694,005

694,005 общая сумма квадратов отклонений зависимой переменной от её выборочного среднего значения.

319,8865 общая сумма квадратов отклонений расчетных по полученному уравнению регрессии значений Y3 от среднего расчетного значения.

374,1188  необъясненная уравнением сумма квадратов отклонений.

F_расч=

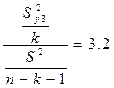
По таблице F-распределения для  уровня значимости a = 0,05, к₁ = 4, к₂ = 20 – 4 – 1 = 15 находим 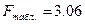. Так как 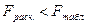, делаем вывод о значимости уравнения множественной регрессии.

Так как по F-критерию найденное уравнение множественной регрессии признано значимым, то имеет смысл оценить степень тесноты связи результирующего показателя с факторами. Оценка тесноты связи проводится с помощью коэффициента множественной детерминации R². По нашим данным:

Регрессионная статистика
Множественный R	0,678917
R-квадрат	0,460928
Стандартная ошибка	4,994122
Наблюдения	20

Полученное уравнение регрессии объясняет 46% дисперсии результирующего показателя.

Параметры уравнения регрессии следует проверить на зна­чимость, т.е. оценить, в какой мере их надо рассматривать как случайные величины. Если вероятность такого события не­велика, то параметры и, следовательно, влияние соответствую­щего признака-регрессора признаются значимыми. Оценка значи­мости обычно проводится с помощью t-критерия. Гипотеза слу­чайности полученной величины А_j  (j = 0,1,2,..к), т.е. незначимости параметра А,    отклоняется с вероятностью ошибки а,  если

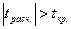
Значение t_KP определяют по таблицам t-распределения для заданного уровня значимости а=0,05  и числа степеней свободы v = n - к – 1=15. Для наших данных t_KP = 2,13. Величина t_расч.  рассчитывается как отношение значения параметра к его среднему квадратическому отклонению.

				Значения границ доверительных интервалов для значений коэффициентов
	Коэффициенты	Стандартная ошибка	t-статистика	нижняя	верхняя
А0	12,70367	7,962561	1,595425	-4,26814	29,67548
А1	-4,58609	3,545411	-1,29353	-12,143	2,970782
А2	6,631436	2,797818	2,370217	0,668025	12,59485
А3	0,01078	0,019186	0,561881	-0,03011	0,051675
А4	-0,07472	0,035112	-2,12817	-0,14956	0,000115

Только коэффициент А2 оказался значимым.

Исключим из уравнения  регрессоры которые оказывают незначительное влияние на результативный показатель. Оставим только значимые полученные из корреляционного анализа факторы. Проанализируем регрессионные зависимости между случайной величиной  Y3 и (Х7, Х12), так при корреляционном анализе мы получили статистически значимые связи между этими переменными.

Найдем и проанализируем свойства оценок регрессии вида:

Y3 = А₀ + А₁ Х7 +А₂ Х12.

Для расчетов воспользуемся встроенным пакетом анализа в EXCEL.

Регрессионная статистика
Множественный R	0,618853182
R-квадрат	0,382979261
Стандартная ошибка	5,018879731
Наблюдения	20

 Данное уравнение регрессии объясняет 38% дисперсии показателя рентабельности производства.

	df- число степеней свободы	Сумма квадратов отклонений (SS)	MS=SS/df	F-расчетное	F-табличное
Регрессия	2	265,7896	132,8948	5,275874	3,59
Остаток	17	428,2156	25,18915
Итого	19	694,0052

694,0052общая сумма квадратов отклонений зависимой переменной от её выборочного среднего значения.

265,7896 общая сумма квадратов отклонений расчетных по полученному уравнению регрессии значений Y3 от среднего расчетного значения.

428,2156 необъясненная уравнением сумма квадратов отклонений.

Для проверки значимости уравнения регрессии используется F- критерий, в нашей задаче по данному критерию нулевая гипотеза о незначимости уравнения отвергается с вероятностью ошибки 5%.

					Значения границ доверительных интервалов  для коэффициентов
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижняя	Верхняя
A0	7,3080	5,5930	1,3066	0,2087	-4,4922	19,1082
A1	7,3037	2,6954	2,7097	0,0149	1,6170	12,9905
A2	-0,0472	0,0283	-1,6659	0,1141	-0,1070	0,0126

По данным значения можно сделать вывод о том что с 5% вероятностью ошибки только коэффициент А₁ является значимым.

Факторный анализ

Вычисление главных факторов проводится по матрице R ли­нейных коэффициентов корреляции между наблюдаемыми признака­ми (X). Из первичных данных берутся только данные по признакам X.  Необходимо привести исходную матрицу в стандартизированный вид, для этого рассчитаем необходимые показатели:

X6		X7		X9		X12
Среднее	0,4445	Среднее	1,5675	Среднее	83,7925	Среднее	116,511
Стандартное отклонение	0,410436	Стандартное отклонение	0,427623	Стандартное отклонение	60,60979	Стандартное отклонение	40,67875

Получаем новую матрицу Z в стандартизированном виде:

-0,5226	-0,2748	1,38422	1,22445
-0,1328	-0,6256	1,68797	-0,5809
-0,0353	-0,4619	2,25471	1,0209
-0,6444	0,19293	1,41079	-0,5544
-0,7175	0,80094	-0,7303	1,41029
-0,2546	0,26308	-0,7158	1,12562
-0,1571	0,87109	0,31624	-0,6871
-0,8637	0,75417	-0,7717	-0,3774
-0,7419	0,87109	-0,6278	1,22445
-0,5713	1,15171	-0,7214	0,59611
-0,0597	0,91786	-0,6328	0,29522
-0,9612	-1,2803	-0,7047	1,50764
-0,3764	0,66063	0,86368	-0,0499
0,08649	-1,6077	-0,6831	-0,5721
-0,0841	-2,2157	-0,7656	0,25097
0,42759	-1,1166	0,29678	-0,6075
0,28141	0,076	-0,598	-1,165
3,20513	-0,1111	-0,8445	-1,2358
2,10873	-0,3917	0,32103	-1,2004
0,0134	1,52588	-0,7399	-1,6252

Матрица линейных коэффициентов корре­ляции (R) полученных переменных (переименуем исходные переменные в  соответственно Х₁, Х₂, Х₃ и Х₄ ) :

	X1	X2	X3	X4
X1	1	-0,17152	-0,07479	-0,57765
X2	-0,17152	1	-0,13231	-0,04563
X3	-0,07479	-0,13231	1	0,029309
X4	-0,57765	-0,04563	0,029309	1

В факторном анализе в исходной матрице R единицы, стоящие на главной диагонали, заменяют показателями "общности" h_i², как доли той дисперсии признака i, которая объясняется действием общих факторов. Определение общностей - одна из проблем факторного анализа. На практике часто используют приближенные приемы, например по максимальному по абсолютной величине элементу столбца (за исключением диагональных).

В нашей задаче получим оценки общностей

h₁²=0,577 ; h₂²= 0,171; h₃²= 0,132; h₄²= 0,577.

Выделение главных факторов связано с нахождением собственных значе­ний и соответствующих им собственных векторов редуцированной корреляционной матрицы, т. е. матрицы коэффициентов корреля­ции, у которой единицы на главной диагонали заменены показа­телями общности. Редуцированную матрицу R будем далее обоз­начать через R_h.

	X1	X2	X3	X4
X1	0,577	-0,17152	-0,07479	-0,57765
X2	-0,17152	0,171	-0,13231	-0,04563
X3	-0,07479	-0,13231	0,132	0,029309
X4	-0,57765	-0,04563	0,029309	0,577

Расчет собственных векторов и собственных чисел, в свою очередь, может быть выполнен итеративным способом.

Для ускорения сходимости используем в расчетах матрицу R_h²:

0,70162	-0,09213	-0,04728	-0,66132
-0,09213	0,078421	-0,02871	0,061015
-0,04728	-0,02871	0,041463	0,070047
-0,66132	0,061016	0,070047	0,670242

 Начнем расчет:

1 итерация	2 итерация	3 итерация
a	b	a	b	a	b
1	-0,0991	-0,708	-1,1823	-1,0154	-1,3885
1	0,0186	0,1329	0,12938	0,11112	0,16056
1	0,03552	0,25373	0,11023	0,09467	0,1188
1	0,13999	1	1,16433	1	1,35518
	0,13999		1,16433		1,35518

4 итерация	5 итерация	6 итерация
a	b	а	b	a	b
-1,0246	-1,3952	-1,025	-1,3956	-1,0251	-
0,11848	0,16218	0,11915	0,16229	0,1192	-
0,08766	0,11873	0,08722	0,11871	0,08719	-
1	1,36118	1	1,36149	1	1,36151
	1,36118		1,36149		1,36151

Из расчетов видно, что на 6-й итерации достигается дос­таточное совпадение результатов. Таким образом, вектор а₆ можно читать первым собственным вектором матрицы R_h, а соот­ветствующее ему собственное значение равно квадратному корню  из мак­симального элемента вектора b₆.

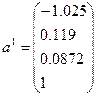- собственный вектор,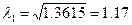

Нагрузки факторов:

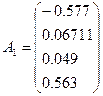
Взаимосвязь исходных признаков, воспроизводимая первым выделенным главным фактором, определяется матрицей воспроизведенных корреляций R₁=A₁A₁^T:

0,33305	-0,0387	-0,0283	-0,3249
-0,0387	0,0045	0,00329	0,03778
-0,0283	0,00329	0,00241	0,02764
-0,3249	0,03778	0,02764	0,31697

Вся остальная корреляция между первичными признаками объясняется действием прочих факторов. Эта оставшаяся необъясненной взаимосвязь описывается матрицей остаточной корре­ляции (R_h - R_t):

0,2440	-0,1328	-0,0465	-0,2527
-0,1328	0,1670	-0,1356	-0,0834
-0,0465	-0,1356	0,1299	0,0017
-0,2527	-0,0834	0,0017	0,2606

Выделим второй главный фактор, оперируя матрицей остаточных корреляций.

Итеративная процедура   определения собственного вектора и собственного числа матрицы R_h в итоге дает:

,

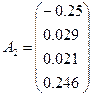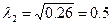
Корреляция переменных, объясняемая действием выделенных двух главных факторов, описывается матрицей R₂:

0,39676	-0,0451	-0,0345	-0,3877
-0,0451	0,00513	0,00392	0,0441
-0,0345	0,00392	0,00299	0,03367
-0,3877	0,0441	0,03367	0,37879

Вся остальная корреляция между первичными признаками объясняется действием прочих факторов. Эта оставшаяся необъясненной взаимосвязь описывается матрицей остаточной корре­ляции (R_h - R_t):

0,1802	-0,1264	-0,0403	-0,1900
-0,1264	0,1664	-0,1362	-0,0897
-0,0403	-0,1362	0,1293	-0,0044
-0,1900	-0,0897	-0,0044	0,1988

Распределение дисперсий принимает следующий вид:

Переменная Хi	Общность h12	Cпецифичность b12	Характерность u12 = 1- h12 - b12
1	0,396	0,18	0,424
2	0,005	0,16	0,835
3	0,003	0,129	0,868
4	0,378	0,198	0,424

В нашей задаче каждый первичный признак объясняет 29% общей дисперсии системы. Первичными признаками, наиболее коррелированными с первым фактором, оказываются уровень потерь от брака и коэффициент оборачиваемости оборотных средств. Общую интерпретацию этих факторов дать затруднительно.  Второй главный фактор объясняет лишь 6,2% дисперсии.

Оценим уровни факторов по каждому отдельному наблюдению:

F1	F2
0,638131	0,277965
-0,14198	-0,06248
0,395674	0,171757
0,068894	0,030067
0,765404	0,334468
0,483693	0,21124
-0,16076	-0,06974
0,190763	0,084048
0,712152	0,311269
0,432823	0,189558
0,134582	0,059198
0,848428	0,369977
0,147893	0,064686
-0,27509	-0,1204
0,06336	0,027005
-0,38926	-0,17038
-0,52026	-0,22674
-1,63435	-0,71379
-1,20446	-0,52626
-0,55564	-0,24144

Рассчитаем корреляцию между F1 и Y3.

	F1	Y3
F1	1
Y3	-0,10539	1

F1 и Y3 слабо коррелируют друг с другом.

Компонентный анализ

Компонентный анализ относится к многомерным методам снижения размерности. Он содержит один метод - метод главных компонент. В этом методе линейные комбинации случайных величин определяются характе­ристическими векторами ковариационной матрицы. Главные компонен­ты представляют собой ортогональную систему координат, в которой дис­персии компонент характеризуют их статистические свойства.

В зависимости от конкретных задач, решаемых в экономике, использу­ется один из методов факторного анализа, или метод главных компонент.

 В процессе компонентного анализа общая дисперсия системы первичных признаков X объясняется только действием общих факторов. В соответствии с нагрузками этих факторов опреде­ляются компоненты общей дисперсии системы:

.

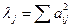Для решения задачи компонентного анализа используют ме­тод главных компонент. Обычно ком­понентный анализ предшествует факторному и используется как инструмент выдвижения гипотез о факторах системы и оценки общностей в факторном анализе. Так же как и в факторном ана­лизе, если выделенные главные компоненты получили содержа­тельную интерпретацию, они используются для расчета индиви­дуальных уровней компонент и их последующего статистического  исследования. Число главных компонент, отбираемых для даль­нейшего использования, определяют теми же приемами, что и в Факторном анализе. Обычно для интерпретации и исследования отбираются только те компоненты, каждый из которых больше, чем на 1, определяет дисперсию системы признаков X, либо те, которые в сумме объясняют большую часть (например, 70-80%) дисперсии системы.

Для выделения первой компоненты определяем первый собс­твенный вектор и соответствующее ему собственное число мат­рицы R коэффициентов корреляции первичных признаков X:

	X6	X7	X9	X12
X6	1	-0,1715	-0,0748	-0,5776
X7	-0,1715	1	-0,1323	-0,0456
X9	-0,0748	-0,1323	1	0,02931
X12	-0,5776	-0,0456	0,02931	1

Итеративная процедура   определения собственного вектора и собственного числа матрицы R в  дает следующие результаты:

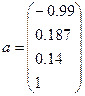- собственный вектор,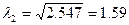

После нормирования   вектор   а преобразуется в вектор С.

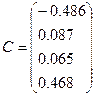
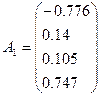
Матрица воспроизведенных корреляций R₁:

0,60342	-0,1091	-0,0818	-0,5803
-0,1091	0,01971	0,01478	0,10489
-0,0818	0,01478	0,01109	0,07866
-0,5803	0,10489	0,07866	0,55809

Матрица остаточных корреляций: R¹ = R - R₁ :

0,39658	-0,0625	0,007	0,00266
-0,0625	0,98029	-0,1471	-0,1505
0,007	-0,1471	0,98891	-0,0493
0,00266	-0,1505	-0,0493	0,44191

Находим собственный вектор и собственное число матрицы R¹:

- собственный вектор,

Тогда для второй компоненты получаем:

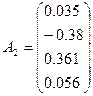
Третья компонента дисперсии системы определяется по матрице остаточной корреляции, объясняемой только третьей и четвертой компонентами

 R’’ =R - (A₁, A₂) (А₁,А₂)^Т

0,39671	-0,0508	-0,0046	0,00025
-0,0508	0,8498	-0,0246	-0,131
-0,0046	-0,0246	0,87431	-0,0672
0,00025	-0,131	-0,0672	0,43916

Находим собственный вектор и собственное число матрицы R^''.

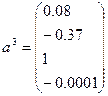- собственный вектор,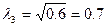

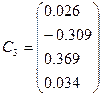
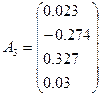
Тогда для третьей компоненты получаем:

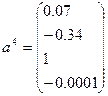- собственный вектор,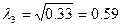

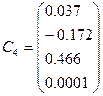
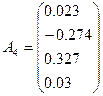
Получаем матрицу С собственных векторов, последовательность собственных чисел и матрицу А – нагрузок компонент:

	-0,486	0,031	0,02689	0,03733
С =	0,087	-0,338	-0,3094	-0,1726
	0,065	0,317	0,36942	0,46657
	0,468	0,049	0,03446	-0.0003

l₁ =1,56;   l₂ =1,14;  l₃ =0,7;   l₄ =0,56.

	-0,776	0,03127	0,02387	0,02720
А =	0,14	-0,3389	-0,2747	-0,12578
	0,105	0,3176	0,32793	0,33995
	0,747	0,04993	0,03059	-0,00003

Основная доля дисперсии приходится на 1-ю и 2-ю компоненты.

Найдем матрицу F =C^T*Z (в матрицу С включаем первые два главных фактора):

F1	F2
0,328403	-0,59221
0,068846	-0,22211
0,101591	-0,72078
0,336419	-0,46209
0,406557	-0,35061
0,154667	-0,0839
0,086233	-0,28735
0,408307	-0,02615
0,416391	-0,37606
0,316231	-0,31868
0,051469	-0,1706
0,46477	0,306949
0,224785	-0,51465
-0,1316	0,861025
-0,03905	0,935163
-0,25712	0,42765
-0,19398	0,384884
-1,62998	0,790967
-1,07317	0,423718
-0,03977	-0,00516

Проводим анализ зависимости между Y₃, F₁ и F₂.

	Y3	F1	F2
Y3	1
F1	0,6113011	1
F2	-0,29479	-0,16015	1

Наблюдается заметная корреляция между Y₃ и F_1. Коэффициент множественной корреляции 0,611.

Уравнение регрессии признака- результата по главным компонентам имеет вид:

Y3=13.25-1.17F1-4.3F2

Дискриминаторный анализ и оптимальная группировка объектов

Дискриминантный анализ как метод многомерной классифика­ции используется для разделения объектов на группы при нали­чии начальных представлений о характере групп. Эти, начальные представления, формализуются как выборки из общей совокупнос­ти объектов,   причем каждая выборке относится к одному строго определенному классу объектов.

В качестве дискриминантных выбраны признаки, полученные в процессе факторного и компонентного анализа. При выделении первой главной компоненты и первого главного фактора наи­большие факторные и компонентные нагрузки связаны с призна­ками Х₆ (уровень потерь от брака) и Х₇ (коэффициент фондоотдачи). Выберем также в качестве дискриминантного один из наиболее нагружен­ных признаков компоненты (фактора) 2, например признак Х₉ (размер основных производственных фондов).

Формируем первую обучающую выборку из объектов 1,2,3. Во вторую обучающую выборку включаем объекты  6,12,15. Эти выборки сформированы на основании размера основных фондов предприятия, который по результатам предыдущего анализа является важным фактором (по этому признаку предприятия можно условно поделить на два класса: мелкие и крупные).

Первая обучающая выборка имеет вид:

Номер объекта	X6	X7	X9
1	0,23	1,45	167,69
2	0,39	1,3	186,1
3	0,43	1,37	220,45

Вектор средних значений:

	0,35
Х1	1,373333
	191,4133

Вторая:

Номер объекта	X6	X7	X9
6	0,34	1,68	40,41
12	0,05	1,02	41,08
15	0,41	0,62	37,39

Вектор средних значений:

 

	0,266667
Х2	1,106667
	39,62667

Определим матрицы рассеивания:

	0,0224	-0,0124	4,9572
U1	-0,0124	0,01127	-1,5259
	4,9572	-1,5259	1434,16
		0,07287	-0,0089	-0,578
	U2	-0,0089	0,57307	1,41167
		-0,578	1,41167	7,72847

Определим элементы обратной матрицы суммарного рассеивания

12,313	0,4422	-0,037
0,4422	1,7273	-0,001
-0,037	-0,001	0,0008

Определим вектор С

	-4,527
C	0,3144
	0,119

 

Посредством дискриминантных множителей приводим массив исходных данных к одномерному представлению ( Z ):

Номер объекта	X6	X7	X9	z
1	0,23	1,45	167,69	19,377
2	0,39	1,3	186,1	20,797
3	0,43	1,37	220,45	24,727
4	0,18	1,65	169,3	19,858
5	0,15	1,91	39,53	4,6272
6	0,34	1,68	40,41	3,7995
7	0,38	1,94	102,96	11,146
8	0,09	1,89	37,02	4,5937
9	0,14	1,94	45,74	5,4211
10	0,21	2,06	40,07	4,467
11	0,42	1,96	45,44	4,1242
12	0,05	1,02	41,08	4,9846
13	0,29	1,85	136,14	15,475
14	0,48	0,88	42,39	3,1499
15	0,41	0,62	37,39	2,7899
16	0,62	1,09	101,78	9,6522
17	0,56	1,6	47,55	3,6284
18	1,76	1,52	32,61	-3,608
19	1,31	1,4	103,25	6,801
20	0,45	2,22	38,95	3,2975

Многомерная средняя первой обучающей выборки (объекты 1, 2, 3) равна

Z₁ = 21,63 .

Многомерная средняя второй обучающей выборки (объекты 6, 12, 15) равна  Z₂ = 3,8.

Граница дискриминации:Z _дискр.= (Z₁ + Z₂)/2 = 12,74.

Итоги дискриминации:

Класс 1 – объекты 1,2,3,4

Класс 2 – объекты 5,6,7,8,9,11,12, 13, 14,15,16,17,18,19,20.