Обработка результатов измерений
Основные
положения теории погрешностей измерений
При
анализе измерений следует четко разграничивать два понятия: истинные значения
физических величин и их эмпирические проявления - результаты измерений.
Истинные значения физических величин - это значения, идеальным образом
отражающие свойства данного объекта как в количественном, так и в качественном
отношении. Они не зависят от средств нашего познания и являются абсолютной
истиной.
Результаты измерений, напротив, являются продуктами нашего познания.
Представляя собой приближенные оценки значений величин, найденные путем
измерения, они зависят не только от них, но еще и от метода измерения, от
технических средств, с помощью которых проводятся измерения, и от свойств
органов чувств наблюдателя, осуществляющего измерения.
Разница
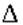между
результатами измерения X' и
истинным значением Q измеряемой
величины называется погрешностью
измерения:
|
|
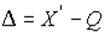
(1)
|
Но
поскольку истинное значение Q
измеряемой величины неизвестно, то неизвестны и погрешности измерения, поэтому
для получения хотя бы приближенных сведений о них приходится в формулу (1)
вместо истинного значения подставлять так называемое действительное значение.
Под
действительным значением
физической величины мы будем понимать ее значение, найденное экспериментально и
настолько приближающееся к истинному, что для данной цели оно может быть
использовано вместо него.
Причинами
возникновения погрешностей являются: несовершенство методов измерений,
технических средств, применяемых при измерениях, и органов чувств наблюдателя.
В отдельную группу следует объединить причины, связанные с влиянием условий
проведения измерений. Последние проявляются двояко. С одной стороны, все
физические величины, играющие какую-либо роль при проведении измерений, в той
или иной степени зависят друг от друга. Поэтому с изменением внешних условий
изменяются истинные значения измеряемых величин. С другой стороны, условия
проведения измерений влияют и на характеристики средств измерений и
физиологические свойства органов чувств наблюдателя и через их посредство
становятся источником погрешностей измерения.
Описанные
причины возникновения погрешностей определяются совокупностью большого числа
факторов, под влиянием которых складывается суммарная погрешность измерения -
см. формулу (1). Их можно объединить в две основные группы.
1.
Факторы, проявляющиеся весьма нерегулярно и столь же неожиданно исчезающие или
проявляющиеся с интенсивностью, которую трудно предвидеть. К ним относятся,
например, перекосы элементов приборов в их направляющих, нерегулярные изменения
моментов трения в опорах, малые флюктуации влияющих величин, изменения внимания
операторов и др.
Доля,
или составляющая, суммарной погрешности измерения (1), определяемая действием
факторов этой группы, называется случайной
погрешностью измерения. Ее основная особенность в том, что она случайно
изменяется при повторных измерениях одной и той же величины.
При
создании измерительной аппаратуры и организации процесса измерения в целом
интенсивность проявления большинства факторов данной группы удается свести к
общему уровню, так что все они влияют более или менее одинаково на формирование
случайной погрешности. Однако некоторые из них, например внезапное падение
напряжения в сети электропитания, могут проявиться неожиданно сильно, в
результате чего погрешность примет размеры, явно выходящие за границы,
обусловленные ходом эксперимента в целом. Такие погрешности в составе случайной
погрешности называются грубыми.
К ним тесно примыкают промахи -
погрешности, зависящие от наблюдателя и связанные с неправильным обращением со
средствами измерений, неверным отсчетом показаний или ошибками при записи
результатов.
2.
Факторы, постоянные или закономерно изменяющиеся в процессе измерительного
эксперимента, например плавные изменения влияющих величин или погрешности
применяемых при измерениях образцовых мер. Составляющие суммарной погрешности
(1), определяемые действием факторов этой группы, называются систематическими погрешностями измерения.
Их отличительная особенность в том, что они остаются постоянными или
закономерно изменяются при повторных измерениях одной и той же величины. До тех
пор, пока систематические погрешности больше случайных, их зачастую можно
вычислить или исключить из результатов измерений надлежащей постановкой опыта.
Таким
образом, мы имеем два типа погрешностей измерения:
- случайные (в
том числе грубые погрешности и промахи), изменяющиеся случайным образом
при повторных измерениях одной и той же величины;
- систематические
погрешности, остающиеся постоянными или закономерно изменяющиеся при
повторных измерениях.
В
процессе измерения оба вида погрешностей проявляются одновременно, и
погрешность измерения можно представить в виде суммы:
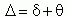
где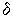 
-
случайная, а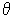 
-
систематическая погрешности.
Например,
если рассмотреть процесс измерения веса какого-либо продукта электронными
весами, то можно выделить систематическую погрешность (из за неправильной
внутренней программы вес продукта завышается или занижается) и случайную
погрешность которая проявляется при повторных измерениях одной и той же
величины.
Для
получения результатов, минимально отличающихся от истинных значений величин,
проводят многократные наблюдения за измеряемой величиной с последующей
математической обработкой опытных данных.
При
проведении измерений целью является оценка истинного значения измеряемой
величины, которое до опыта неизвестно. Результат измерения включает в себя
помимо истинного значения еще и случайную погрешность, следовательно, сам
является случайной величиной. В этих условиях фактическое значение случайной
погрешности, полученное при поверке, еще не характеризует точности измерений,
поэтому не ясно, какое же значение принять за окончательный результат измерения
и как охарактеризовать его точность.
Ответ
на эти вопросы можно получить, используя при метрологической обработке
результатов измерения методы математической статистики, имеющей дело именно со
случайными величинами.
Прямыми называются измерения, в результате которых искомое значение
физической величины находят непосредственно из опытных данных. Прямые измерения
осуществляются путем многократных наблюдений. Результаты наблюдений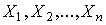 
называются
равнорассеянными, если они
являются независимыми, одинаково распределенными случайными величинами.
Равнорассеянные результаты получают при измерениях, проводимых одним
наблюдателем или группой наблюдателей с помощью одних и тех же методов и
средств измерений в неизменных условиях внешней среды.
Обработка
результатов наблюдений в соответствии с методикой прямых измерений с
многократными наблюдениями производится в следующем порядке:
1.
Определяется среднее арифметическое полученных данных:
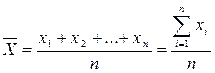
2. Определяется среднеквадратическая погрешность ряда измерений
СКП (синоним СКО - среднеквадратическое отклонение):
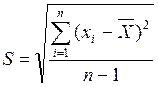
3. Определяется наличие
промахов (грубых погрешностей) в ряду измерений, т.е. таких измерений, которые
существенно отличаются от остальных.
Один из критериев определения промаха: сравнивают погрешность
ΔXi которая определяется по формуле ΔХi = Xi-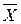
с предельной
погрешностью, равной 3S (правило 3-х сигм). Измерение
считается промахом, если ΔXi >3S. В
этом случае значение Xi исключают из общего
числа измерений и обработку ряда измерений начинают заново и снова рассчитывают
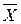и S.
4. Определяется среднеквадратическая погрешность среднего
арифметического по формуле:
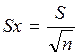
5. Находится
доверительный интервал (доверительные границы) для
среднего значения по формуле (Р) = 
t*Sx., где t- коэффициент, зависящий
от заданной доверительной вероятности Р и числа измерений n.
Sx- СКП (СКО) среднего
арифметического. Коэффициент t определяется по таблице распределения
Стьюдента при различной доверительной вероятности.
6. Записывается действительный результат
измерений с заданной доверительной вероятностью Р:
Xg=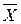(P).
Решение задачи по оценке погрешности многократных
измерений
При обработке
результатов прямых равноточных наблюдений
необходимо получить оценку действительного значения измеряемой величины,
для заданной доверительной вероятности определить
доверительный интервал для среднего значения, оценить ряд измерений
на наличие промахов.
Исходные
данные представлены в таблице 1.
|
Номер наблюдения
|
Значение измеряемой величины (кг)
|
|
1
|
46,28
|
|
2
|
46,281
|
|
3
|
46,287
|
|
4
|
46,287
|
|
5
|
46,281
|
|
6
|
46,288
|
|
7
|
46,28
|
|
8
|
46,289
|
|
9
|
46,281
|
|
10
|
46,282
|
Мы получили ряд наблюдений состоящий из 10 измерений.
Теперь по методике обработки прямых равноточных измерений
произведем следующие вычисления:
1. Определим среднее арифметическое полученных данных:
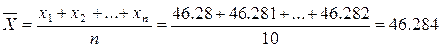
2. Вычислим среднеквадратическая погрешность ряда измерений СКП (синоним
СКО - среднеквадратическое отклонение):
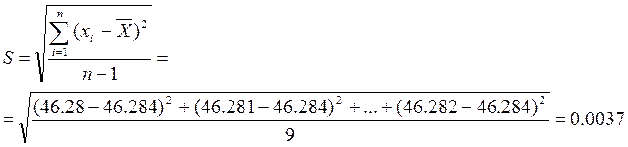3.
Определим наличие промахов (грубых погрешностей) в ряду измерений.
Один из
критериев определения промаха: сравнивают абсолютное значение погрешности
ΔXi которая определяется по формуле ΔХi = |Xi-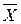| с предельной погрешностью, равной 3S (правило 3-х сигм).
Измерение считается промахом, если ΔXi >3S. В
этом случае значение Xi исключают из общего
числа измерений и обработку ряда измерений начинают заново и снова рассчитывают
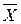и S.
3S=0,011
|
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
ΔХi
|
0,0036
|
0,0026
|
0,0034
|
0,0034
|
0,0026
|
0,0044
|
0,0036
|
0,0054
|
0,0026
|
0,0016
|
Ни одно из
значений погрешностей по модулю не превышает 3S. Это означает отсутствие
промахов в ряде измерений.
4. Рассчитаем среднеквадратическая погрешность среднего
арифметического по формуле:
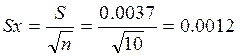
5. Найдем
доверительный интервал (доверительные границы) для
среднего значения по формуле (Р) = t*Sx, где t- коэффициент, зависящий
от заданной доверительной вероятности Р и числа измерений n.
Sx- СКП (СКО) среднего
арифметического. Коэффициент t определяется по таблице
распределения Стьюдента при различной доверительной вероятности. По таблице при
заданном значении вероятности Р=0,8 и n=10, значение t=1,38.
(Р)
= 1,38*0,0012=0,0016
6. Запишем действительный результат
измерений с заданной доверительной вероятностью Р:
Xg=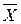(P)=46,2840,0016
Итак
действительный результат измерений с вероятностью 80% лежит в интервале от
46,2824 до 46,2856 кг.