МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО – ЭКОНОМИЧЕСКИЙ

ИНСТИТУТ

Лабораторная работа

по дисциплине:

«Экономико – математическое моделирование»

Вариант № 5

    

Смоленск

2006г.

Задача 2. Провести моделирование и решить специальную задачу линейного программирования.

Транспортная задача

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1тонны песка с карьеров на ремонтные участки.

Числовые данные для решения содержатся ниже в матрице планирования.

Требуется:

1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2) Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ?; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами?

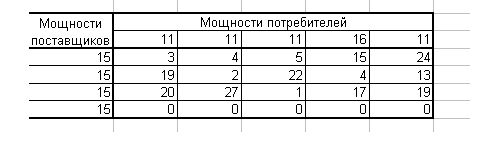
2.5. Матрица планирования:

Участки работ Карьеры	В1	В2	В3	В4	В5	Предложение
А1	3	4	5	15	24	15
А2	19	2	22	4	13	15
А3	20	27	1	17	19	15
Потребности	11	11	11	16	11

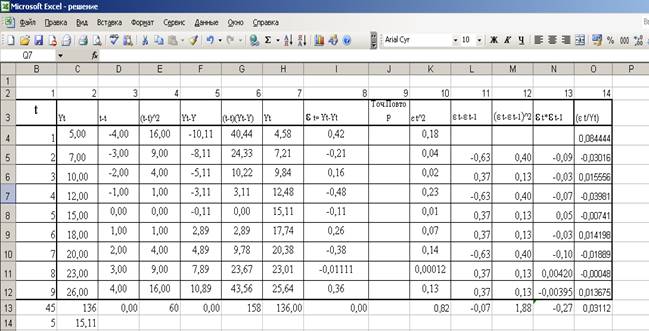
Решение:

1)

В данной задаче суммарные запасы не равны суммарным потребностям, т.е.:

∑ai ≠∑bj,

поэтому данная задача является открытой. Для того, что бы перевести задачу в закрытый тип введем фиктивного поставщика.

Теперь в задаче суммарные запасы равны суммарным потребностям, т.е.:

∑ai =∑bj,

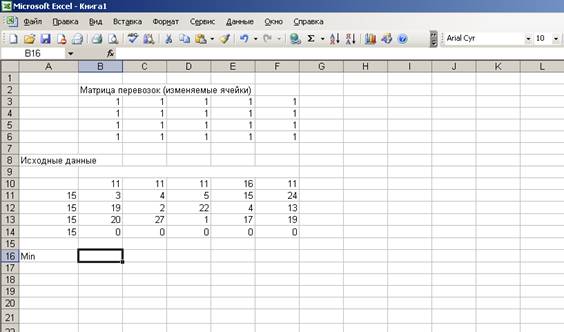
1.     Создаем форму для решения задачи и вводим исходные данные (результата будет помещен в ячейках B3:F6, оптимальное значение ЦФ – в ячейке B16):

2. Вводим граничные условия

2.1. Вводим условия реализации мощностей поставщиков

ai = ∑xij, где  ai – мощность поставщика, xij – объем поставки груза от поставщика I к потребителю j; n – количество потребителей.

2.2. Вводим условия удовлетворения запросов потребителей

bi = ∑xij, где bi – мощность потребителя, m – количество поставщиков.

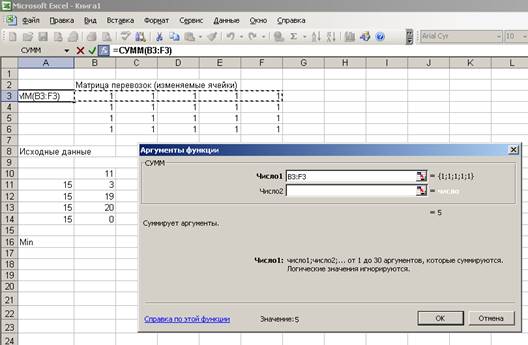
3. Используя Мастер функций вводим формулу для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза. Блок ячеек B3:B6 содержит объем поставок для каждого потребителя, в блоке B8:F10 содержаться удельные затраты на доставку груза:

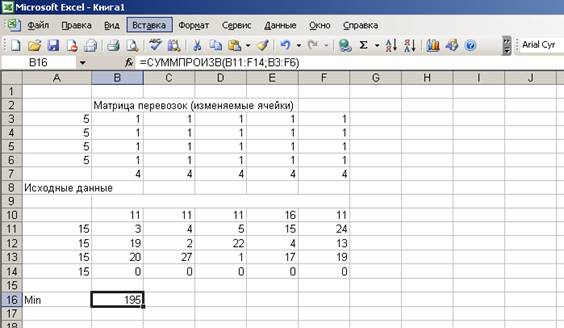
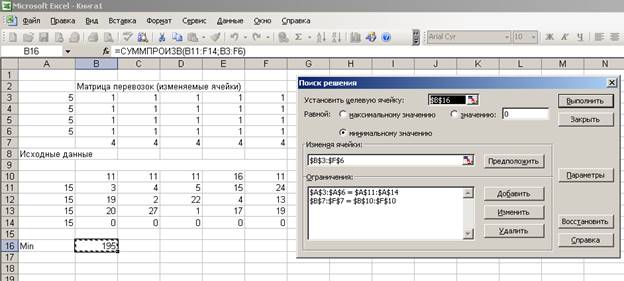
4. Запускаем программу Поиск решения. Назначаем ячейку для целевой функции (B16) и вводим её тип – минимальное значение, указываем адреса изменяемых ячеек (F3: F6), вводим ограничения и параметры:

5.                В результате получаем оптимальный план перевозок:

 

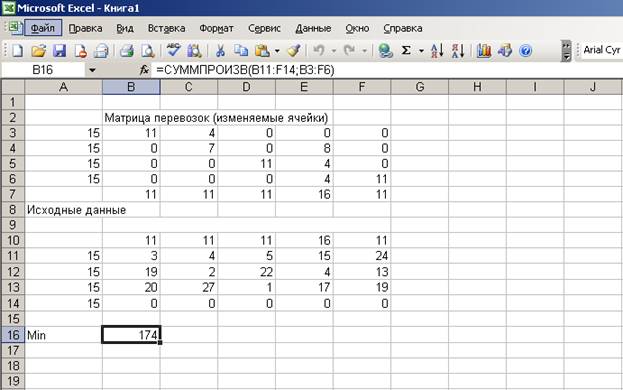
Вывод:

План перевозок означает, что:

Х11 = 11 тонн песка следует перевезти с карьера А1 на участок В1 ремонта автодорог;

Х12 = 4 тонны песка следует перевезти с карьера А1 на участок В2 ремонта автодорог;

Х22 = 7  тонн песка следует перевезти с карьера А2 на участок В2 ремонта автодорог;

Х33 = 11 тонн песка следует перевезти с карьера А2 на участок В5 ремонта автодорог;

Х24 =8 тонн песка следует перевезти с карьера А2 на участок В4 ремонта автодорог;

X34= 4 тонны песка следует перевезти с карьера А3 на участок В4 ремонта автодорог;

X44= 4 тонны песка следует перевезти с карьера А4 на участок В4 ремонта автодорог;

Х45 = 11 тонн песка следует перевезти с карьера А3 на участок В3 ремонта автодорог;

Общая стоимость перевозок = 174

2) а) Если появится запрет на перевозки от первого карьера до второго участка работ,

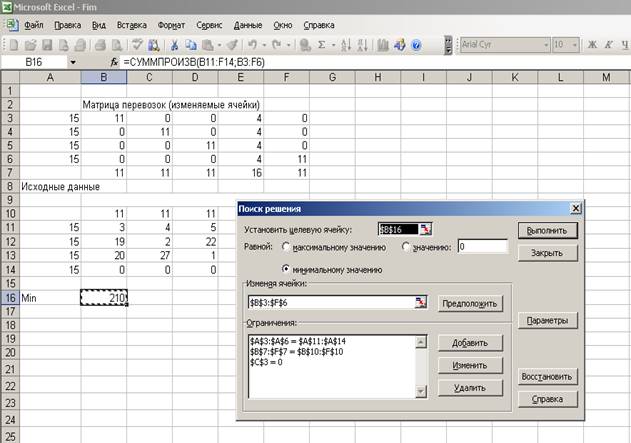
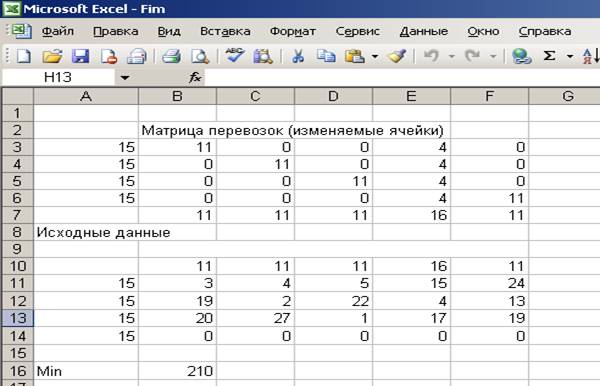
то оптимальный план перевозок песка на участки автодорог уменьшится.

Общая стоимость перевозок будет равна 210.

б) Если по 2-му карьеру будет ограничен объем перевозок 3 тоннами,

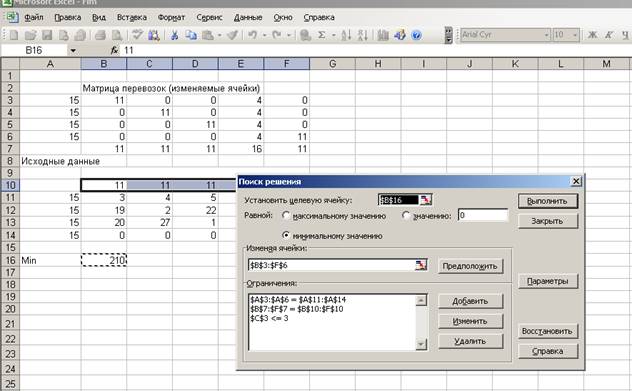
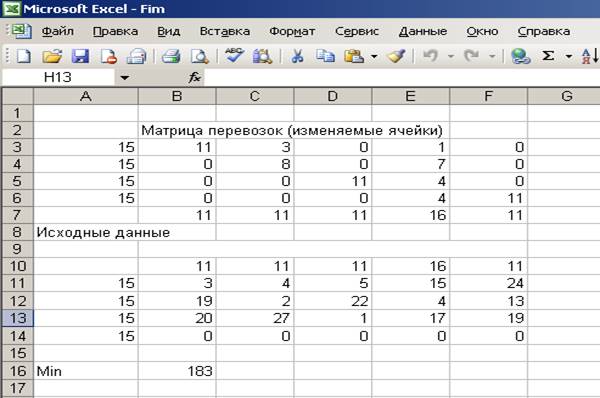
то оптимальный план перевозки песка на участки автодорог уменьшится. Общая стоимость перевозок будет равна 183.

Задача 1. Предложить оптимальное управленческое решение в следующих типовых хозяйственных ситуациях.

Задача о рационе

 

 Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500 г = 0,5 кг.

Для того, чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.

В таблице приведены данные, характеризующие содержание (по весу) питательных веществ к каждом из ингредиентов и удельную стоимость каждого ингредиента

                                                                                            

Ингредиент	Содержание питательных веществ (кг/ингредиент)	Стоимость (руб./кг)
Кальций	Белок	Клетчатка
Известняк Зерно Соевые бобы	0.38 0.001 0.002	– 0.09 0.50	– 0.02 0.08	0.4 0.15 0.40

Смесь должна содержать (от общего веса смеси):

не менее 0, 8% кальция;

не менее 22% белка;                    

не более 5% клетчатки.

Требуется определить количество (в кг) каждого из трёх ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и её питательности.

       

  Решение:

1)    Экономико – математическая модель.

Введем следующие обозначения: X1 – количество известняка в смеси, X2 – количество зерна в смеси, X3 – количество соевых бобов в смеси.

В данной задаче необходимо минимизировать целевую функцию:

F(x)= 0,4X1 + 0,15X2 + 0,40X3→max.

Вычислим количество питательных веществ от всего корма за данный период. Для этого вычислим количество корма в целом

8(недель) * 20000(цыплят) * 0,5(кг. корма) = 80000

Вычислим общее количество ингредиентов

Кальций: 0,8% = 0,008

                 80000 * 0,008 = 640 кг кальция всего.

Белка: 22% = 0,22

            80000 * 0,22 = 17600 кг. белка всего

Клетчатки: 5% = 0,05

                    80000 * 0,05 = 4000 кг. клетчатки всего

1.     Ограничения по содержанию кальция:

0,38X1 + 0,001X2 + 0,002X3 ≥ 640

2.     Ограничения по содержанию белка:

     0,09X2 + 0,50X3 ≥ 17600

     3. Ограничения по содержанию клетчатки:

     0,02X2 + 0,08X3 ≤ 4000

2)    Используем для нахождения оптимального расхода ингредиентов табличный процессор Excel:

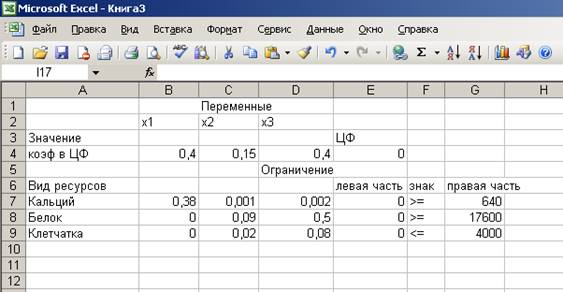
1.     Создаем форму и вводим условия задачи (результат решения будет помещен в ячейках B3 : D3, оптимальное значение ЦФ – в ячейке F4):

2.     Вводим зависимость для целевой функции:

 

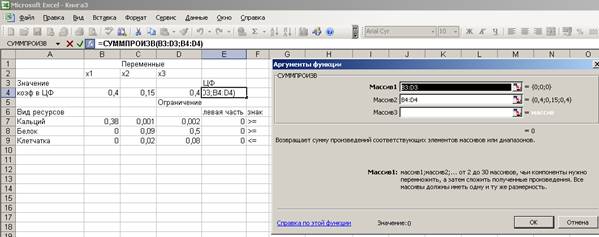
3.     Вводим зависимость для ограничений:

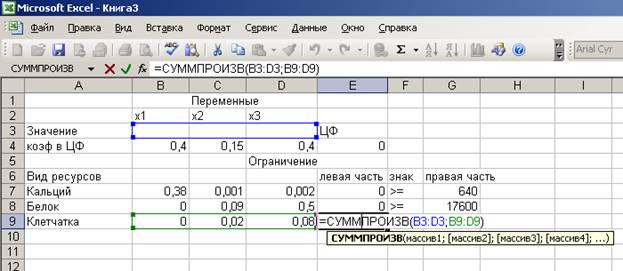
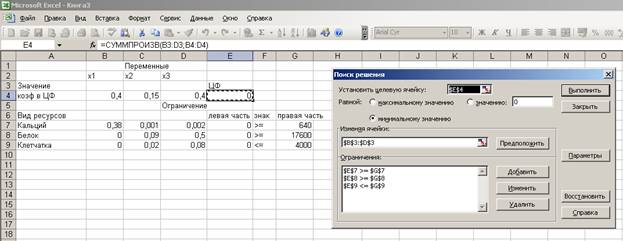
4.     Запускаем команду Поиск решения. Назначаем ячейку для целевой функции (Е4) и вводим ее тип – минимальное значение, указываем адреса изменяемых ячеек (В3 : D3), вводим ограничения:

5.     Вводим параметры для решения задачи:

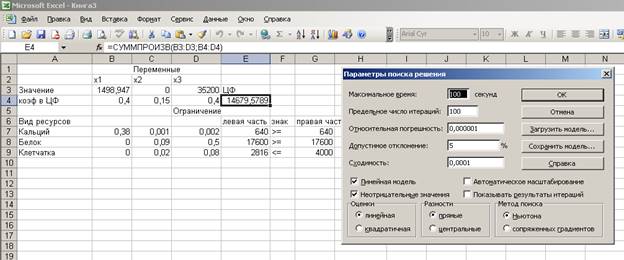
6.     Результаты поиска решения и исходная таблица с заполненными ячейками В3 : D3 для значений Xi и ячейка Е4 с минимальным значением целевой функции:

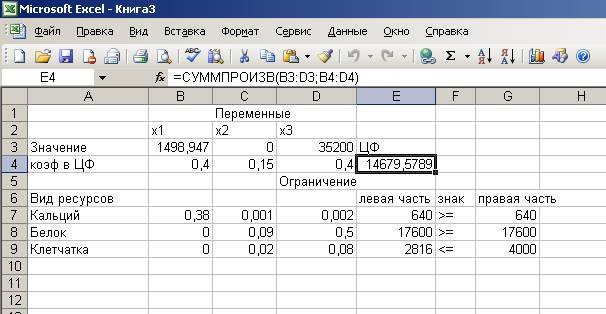
Вывод:

Для получения смеси минимальной стоимости, при соблюдении требований к ее питательности необходимо: 1498,947 кг. известняка, 0 кг. зерна и 35200 кг. соевых бобов.