ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №2
«Автоматизированный
корреляционно-регрессионный
анализ взаимосвязи статистических
данных в среде MS Excel»
Вариант №_10_
Выполнил: ст. III курса
Проверил:
Резяпова А.А.
Уфа, 2006г.
Постановка задачи
Корреляционно-регрессионный анализ взаимосвязи
признаков является составной часть проводимого статистического исследования
двух экономических показателей статистической совокупности 32 предприятий и
частично использует результаты Лабораторной работы №1.
В Лабораторной работе №2 изучается
взаимосвязь между факторным признаком Среднегодовая
стоимость основных производственных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y), значениями которых являются
исходные данные Лабораторной работы № 1 после исключения из них аномальных
значений (Таблица 1а).
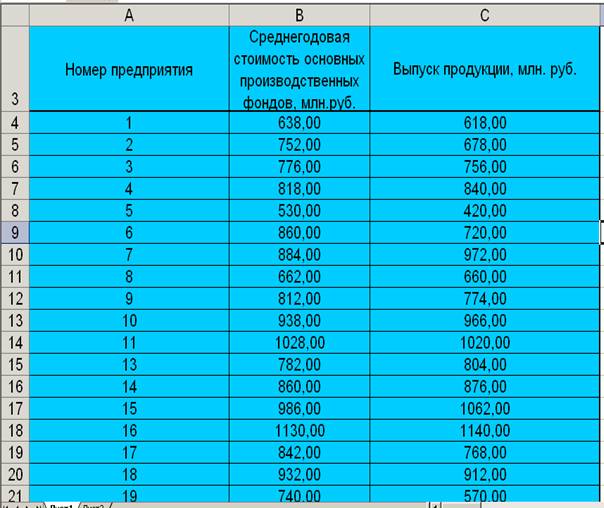
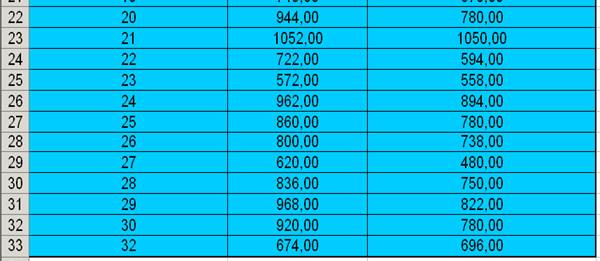
Таблица
1а
Исходные
данные
В
процессе статистического исследования необходимо решить ряд задач.
1. Установить наличие статистической связи между факторным
признаком Х и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных
рядов.
2. Установить наличие корреляционной связи между признаками Х и Y методом аналитической
группировки.
3. Оценить тесноту связи
признаков Х и Y на основе:
а) эмпирического корреляционного
отношения h;
б) линейного коэффициента корреляции r.
4. Построить однофакторную
линейную регрессионную модель связи признаков Х
и Y, используя
инструмент Регрессия
надстройки Пакет анализа.
5. Оценить адекватность и
практическую пригодность построенной линейной
регрессионной модели, указав:
а) доверительные интервалы
коэффициентов а , а
, а ;
;
б) степень тесноты связи признаков
Х и Y;
в) погрешность регрессионной модели.
6. Дать экономическую
интерпретацию:
а) коэффициент регрессии а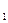 ;
;
б) коэффициента эластичности К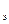 ;
;
в) остаточных величин e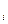 .
.
7. Найти наиболее адекватное
нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм.
Построить для этого уравнения теоретическую кривую регрессии.
Алгоритмы
выполнения всех заданий.
Распечатка
рабочего файла с результативными таблицами
и графиками
Выполняются три задания:
Задание 1.
Построение
аналитической группировки для выявления корреляционной зависимости
результативного признака от факторного и оценка тесноты взаимосвязи этих
признаков.
Задание
2. Построение однофакторной линейной регрессионной модели связи изучаемых
признаков с помощью инструмента Регрессии
надстройки Пакет анализа.
Задание 3. Построение однофакторных
нелинейных регрессионных моделей связи признаков с помощью инструмента Мастер
диаграмм и выбор наиболее адекватного уравнения регрессии.
Алгоритмы
выполнения Задания 1
Задача 1. Построение аналитической группировки предприятий
по признаку Среднегодовая стоимость основных
производственных фондов
Этап 1. Ранжирование единиц совокупности по возрастанию
факторного
признака Среднегодовая стоимость основных
производственных фондов
Алгоритм
1.1. Ранжирование исходных данных.
1.
Выделить исходные данные таблицы 1 (А4:С33);
2. ДанныеÞСортировка;
3. Сортировать поÜ
заголовок столбца, по которому выполняется сортировка, т.е. Среднегодовая
стоимость основных производственных фондов;
4. по возрастанию / по убыванию –
устанавливается в положение по
возрастанию;
5. Затем и В последнюю очередь по – не активизируются;
6. Идентифицировать поля по подписям /
обозначениям столбцов листа – устанавливается в положение подписями;
8. ОК
В результате
указанных действий в таблице 1б размещаются данные, ранжированные по
возрастанию признака Среднегодовая стоимость основных производственных фондов.
Таблица1б
Исходные
данные
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
5
|
530,00
|
420,00
|
|
23
|
572,00
|
558,00
|
|
27
|
620,00
|
480,00
|
|
1
|
638,00
|
618,00
|
|
8
|
662,00
|
660,00
|
|
32
|
674,00
|
696,00
|
|
22
|
722,00
|
594,00
|
|
19
|
740,00
|
570,00
|
|
2
|
752,00
|
678,00
|
|
3
|
776,00
|
756,00
|
|
13
|
782,00
|
804,00
|
|
26
|
800,00
|
738,00
|
|
9
|
812,00
|
774,00
|
|
4
|
818,00
|
840,00
|
|
28
|
836,00
|
750,00
|
|
17
|
842,00
|
768,00
|
|
6
|
860,00
|
720,00
|
|
14
|
860,00
|
876,00
|
|
25
|
860,00
|
780,00
|
|
7
|
884,00
|
972,00
|
|
30
|
920,00
|
780,00
|
|
18
|
932,00
|
912,00
|
|
10
|
938,00
|
966,00
|
|
20
|
944,00
|
780,00
|
|
24
|
962,00
|
894,00
|
|
29
|
968,00
|
822,00
|
|
15
|
986,00
|
1062,00
|
|
11
|
1028,00
|
1020,00
|
|
21
|
1052,00
|
1050,00
|
|
16
|
1130,00
|
1140,00
|
Этап 2. Распределение предприятий по группам
Алгоритм 1.2. Выделение групп предприятий с помощью заливки контрастным
цветом
1.
Из всего диапазона
отсортированных данных А4:С33 выделить мышью диапазон ячеек первой группы, для чего необходимо
отсчитать в ранжированном ряду количество строк, соответствующее числу
предприятий первой группы ;
2. Нажать на панели
инструментов кнопку заливки;
3. Выбрать цвет по собственному
усмотрению;
4. Выполнить действия 1-3 для всех групп, выбирая контрастные цвета
для цветовой заливки очередной группы.
Результат работы алгоритмов 1.1 и 1.2 в таблице 1в.
Таблица1в
Исходные
данные
|
Номер предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
5
|
530,00
|
420,00
|
|
23
|
572,00
|
558,00
|
|
27
|
620,00
|
480,00
|
|
1
|
638,00
|
618,00
|
|
8
|
662,00
|
660,00
|
|
32
|
674,00
|
696,00
|
|
22
|
722,00
|
594,00
|
|
19
|
740,00
|
570,00
|
|
2
|
752,00
|
678,00
|
|
3
|
776,00
|
756,00
|
|
13
|
782,00
|
804,00
|
|
26
|
800,00
|
738,00
|
|
9
|
812,00
|
774,00
|
|
4
|
818,00
|
840,00
|
|
28
|
836,00
|
750,00
|
|
17
|
842,00
|
768,00
|
|
6
|
860,00
|
720,00
|
|
14
|
860,00
|
876,00
|
|
25
|
860,00
|
780,00
|
|
7
|
884,00
|
972,00
|
|
30
|
920,00
|
780,00
|
|
18
|
932,00
|
912,00
|
|
10
|
938,00
|
966,00
|
|
20
|
944,00
|
780,00
|
|
24
|
962,00
|
894,00
|
|
29
|
968,00
|
822,00
|
|
15
|
986,00
|
1062,00
|
|
11
|
1028,00
|
1020,00
|
|
21
|
1052,00
|
1050,00
|
|
16
|
1130,00
|
1140,00
|
Этап 3. Расчет суммарных и средних групповых значений
результативного
признака Y – Выпуск продукции
Алгоритм 1.3. Расчет суммарных групповых значений результативного признака
1. В ячейке (D41),
для суммарного значения результативного
признака Выпуск продукции первой группы,
перед формулой поставить знак равенства «=»;
2. В качестве аргумента функции
указать диапазон ячеек из таблицы 1в с
результативными значениями у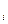 первой группы (визуально легко определяется по цвету заливки
диапазона);
первой группы (визуально легко определяется по цвету заливки
диапазона);
3.
Enter;
4. Выполнить действия 1-3
поочередно для всех групп, используя цветовые заливки диапазонов.
Алгоритм
1.4. Расчет средних групповых значений результативного признака
1. В ячейке (Е41), для среднего значения признака Выпуск продукции, относящихся к первой группе, перед формулой поставит
знак равенства «=»;
2. Enter;
3.
Выполнить действия 1-2 поочередно для всех
групп.
Для расчета итоговых сумм в табл. (в ячейках C46, D46, E46) перед формулами
необходимо поставить знак равенства «=».
Результат работы алгоритмов 1.3 и 1.4 в
таблице 2.
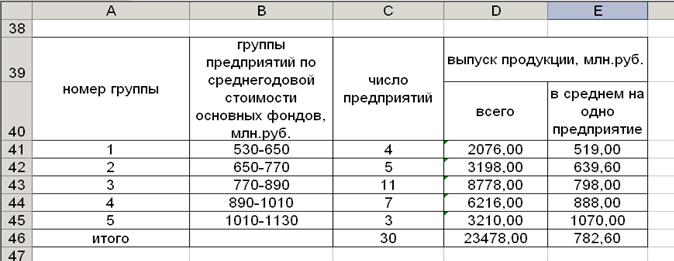
Таблица 2
Зависимость
выпуска продукции от среднегодовой
стоимости основных
фондов
Задача 2. Оценка тесноты связи изучаемых признаков
на основе
эмпирического корреляционного отношения
Алгоритм 2.1. Расчет внутригрупповых дисперсий результативного признака
1. В ячейке D52:D56,
для внутригрупповых дисперсий первой группы (D52),
перед формулой поставить знак равенства «=»;
2. В качестве аргумента
функции указать диапазон ячеек из
таблицы 2в с ранжированными значениями у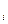 первой группы – визуально легко определяется по цвету заливки
диапазона;
первой группы – визуально легко определяется по цвету заливки
диапазона;
3.
Enter;
4. Выполнить действия 1-3
поочередно для всех групп, используя
цветовые заливки диапазонов.
Для расчета итоговых сумм в таблице 3 (в ячейках C57, D57) перед формулами
необходимо поставить знак равенства «=».
Результат работы алгоритма 2.1 в таблице 3
Таблица 3
Показатели
внутригрупповой вариации
Алгоритм 2.2. Расчет общей, средней из
внутригрупповых и факторной
дисперсий
В ячейках В63, для общей дисперсии (А63),
для средней из внутригрупповых дисперсий (В63)
и для значения факторной дисперсии (С63) перед формулами необходимо поставить
знак равенства «=».
Алгоритм
2.3. Расчет эмпирического корреляционного отношения
1. В ячейке, для эмпирического
корреляционного отношения (D63) перед формулой поставить
знак равенства «=»;
2. Enter;
В результате работы алгоритмов 2.2 – 2.3 Excel
осуществляет вывод результатов расчета показателей (Таблица 4).
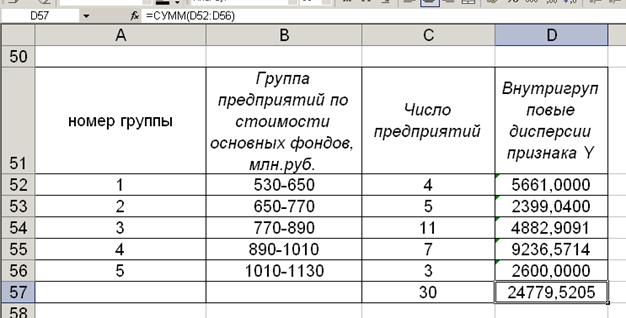
Таблица 4
Показатели
дисперсии и эмпирического
корреляционного отношения
Задача 3. Оценка тесноты связи изучаемых признаков
на основе линейного коэффициента корреляции
Алгоритм
3.1. Расчет линейного коэффициента корреляции
1. Сервис Þ Анализ данных Þ Корреляция Þ ОК.
2. Входной интервал Ü диапазон ячеек таблицы 1в
со значениями факторного и результативного признаков (В4:С33);
3. Группирование – по столбцам;
4. Метки в первой строке – не активизировать;
5. Выходной интервал – адрес ячейки заголовка первого столбца выходной таблицы 5 (А68);
6. Новый рабочий лист и Новая рабочая книга – не
активизировать;
7. ОК.
В результате работы алгоритма 3.1 Excel
выдает оценку тесноты связи факторного и результативного признаков (Таблица 5).
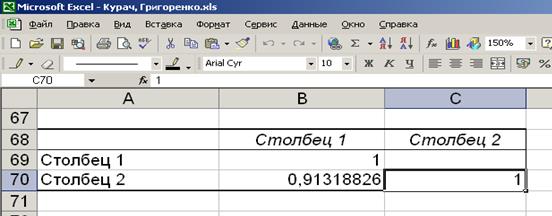
Таблица 5
Линейный
коэффициент корреляции признаков
Алгоритм выполнения Задания 2
Алгоритм 1. Расчет параметров уравнения линейной
регрессии и проверка его
адекватности фактическими данными
1. Сервис Þ Анализ данных Þ Регрессия Þ ОК;
2. Входной интервал Y Ü диапазон ячеек таблицы со
значениями признака Y – Выпуск продукции (С4:С33);
3. Входной интервал Х Ü диапазон ячеек таблицы со значениями признака Х –
Стоимость основных фондов (В4:В33);
4. Метки в первой строке / Метки в первом столбце – не активизировать;
5. Уровень надежности Ü 68,3;
6. Константа – ноль – не активизировать;
7. Выходной интервал Ü адрес ячейки заголовка
первого столбца первой выходной результативной таблицы (А75);
8. Новый рабочий лист и Новая рабочая книга – не
активизировать;
9. Остатки – активизировать;
10.
Стандартизованные остатки – не активизировать;
11.
График остатков – не активизировать;
12.
График подбора – не активизировать;
13.
График нормальной вероятности – не активизировать;
14.
ОК;
15.
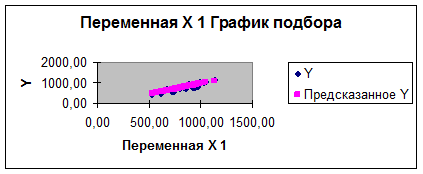
Полученный график необходимо
расположить после выходных таблиц, начиная с ячейки А135.
В результате
указанных действий осуществляется вывод в заданный диапазон рабочего
файла четырех выходных таблиц и одного графика, начиная с ячейки, указанной в
поле Выходной интервал.
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
Регрессионная
статистика
|
|
Множественный
R
|
0,91318826
|
|
R-квадрат
|
0,833912798
|
|
Нормированный
R-квадрат
|
0,827981112
|
|
Стандартная
ошибка
|
71,80244515
|
|
Наблюдения
|
30
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
724804,6484
|
724804,6484
|
140,5861384
|
1,97601E-12
|
|
Остаток
|
28
|
144356,5516
|
5155,59113
|
|
|
|
Итого
|
29
|
869161,2
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
-121,5648002
|
77,37501409
|
-1,571111833
|
0,127389835
|
|
Переменная
X 1
|
1,089355181
|
0,09187519
|
11,85690257
|
1,97601E-12
|
|
Нижние 95%
|
Верхние 95%
|
Нижние 68,3%
|
Верхние 68,3%
|
|
-280,0605096
|
36,93090926
|
-200,397899
|
-42,73170141
|
|
0,901157173
|
1,277553188
|
0,995748659
|
1,182961703
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
455,7934457
|
-35,79344571
|
|
2
|
501,5463633
|
56,45363669
|
|
3
|
553,835412
|
-73,835412
|
|
4
|
573,4438053
|
44,55619474
|
|
5
|
599,5883296
|
60,4116704
|
|
6
|
612,6605918
|
83,33940823
|
|
7
|
664,9496405
|
-70,94964046
|
|
8
|
684,5580337
|
-114,5580337
|
|
9
|
697,6302959
|
-19,63029589
|
|
10
|
723,7748202
|
32,22517977
|
|
11
|
730,3109513
|
73,68904869
|
|
12
|
749,9193446
|
-11,91934457
|
|
13
|
762,9916067
|
11,00839326
|
|
14
|
769,5277378
|
70,47226217
|
|
15
|
789,1361311
|
-39,13613109
|
|
16
|
795,6722622
|
-27,67226217
|
|
17
|
815,2806554
|
-95,28065543
|
|
18
|
815,2806554
|
60,71934457
|
|
19
|
815,2806554
|
-35,28065543
|
|
20
|
841,4251798
|
130,5748202
|
|
21
|
880,6419663
|
-100,6419663
|
|
22
|
893,7142285
|
18,28577154
|
|
23
|
900,2503595
|
65,74964046
|
|
24
|
906,7864906
|
-126,7864906
|
|
25
|
926,3948839
|
-32,39488389
|
|
26
|
932,931015
|
-110,931015
|
|
27
|
952,5394082
|
109,4605918
|
|
28
|
998,2923258
|
21,70767417
|
|
29
|
1024,43685
|
25,56314983
|
|
30
|
1109,406554
|
30,59344571
|
Алгоритм выполнения Задания 3
Алгоритм
1. Построение уравнений регрессионных моделей для различных видов
зависимости признаков с
использованием средств инструмента
Мастер диаграмм
1. Выделить мышью диаграмму
рассеяния, расположенную начиная с ячейки Е4,
и увеличить масштаб диаграммы на весь экран;
2. Диаграмма Þ Добавить линию тренда;
3. Выбрать вкладку Тип, задать вид регрессионной модели – полином 2-го порядка;
4. Выбрать вкладку Параметры и выполнить действия:
1. Переключатель Название аппроксимирующей кривой:
автоматическое / другое – установить
в положение автоматическое;
2. Поле Прогноз вперед на – не активизировать;
3. Поле Прогноз назад на – не активизировать;
4. Флажок Пересечение кривой с осью Y в точке – не активизировать;
5. Флажок Показывать уравнение на диаграмме – активизировать;
6. Флажок Поместить на диаграмму величину достоверности аппроксимации R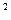 - активизировать;
- активизировать;
7. ОК;
8. Установить курсор на линию
регрессии и щелкнуть правой клавишей мыши;
9. В появившемся диалоговом
окне Формат линии тренда выбрать
тип, цвет и толщину линии;
10.
ОК;
11.
Вынести уравнение и коэффициент R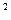 за корреляционное поле. При необходимости уменьшить размер
шрифта.
за корреляционное поле. При необходимости уменьшить размер
шрифта.
5. Действия 3-4 (в п.4 – шаги
1-11) выполнить поочередно для следующих видов регрессионных моделей:
-
полином 3-го порядка;
-
степенная;
-
экспоненциальная.
Переместить Диаграмму 1 в конец рабочего файла,
начиная с ячейки А155.
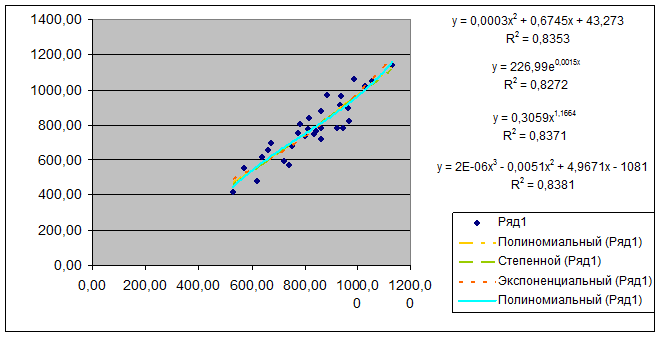
В результате указанных действий для
выбранных видов моделей регрессии осуществляется вывод на диаграмму рассеяния
четырех уравнений регрессии, их графиков и значений соответствующих
коэффициентов детерминации R (Диаграмма 1).
(Диаграмма 1).
Диаграмма
1
Уравнения
регрессии и их графики
Алгоритм
2. Построение наиболее адекватного уравнения регрессии
1. Путем визуального анализа
значений R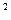 выбрать по
максимальной величине R
выбрать по
максимальной величине R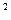 наиболее
адекватное уравнение регрессии;
наиболее
адекватное уравнение регрессии;
2. Выделить диаграмму
рассеяния, расположенную начиная с ячейки Е20;
3. Диаграмма Þ Добавить линию тренда;
4. Выбрать вкладку Тип и задать вид наиболее адекватной
нелинейной регрессионной модели;
5. Выбрать вкладку Параметры:
1. Переключатель Название аппроксимирующей кривой:
автоматическое / другое – установить в положение автоматическое;
2. Поле Прогноз вперед на – не активизировать;
3. Поле Прогноз назад на – не активизировать;
4. Флажок Пересечение кривой с осью Y в точке – не активизировать;
5. Флажок Показывать уравнение на диаграмме – активизировать;
6. Флажок Поместить на диаграмму величину достоверности аппроксимации R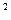 - активизировать;
- активизировать;
7.
ОК.
Переместить Диаграмму 2 в конец рабочего файла,
начиная с ячейки А190.
В результате указанных действий осуществляется вывод
на диаграмму рассеяния уравнения регрессии для выбранной наиболее адекватной
модели регрессии, ее графика и значения коэффициента детерминации R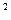 (Диаграмма 2).
(Диаграмма 2).
Диаграмма 2
Наиболее адекватное уравнение регрессии и его график

Выводы по результатам выполнения
лабораторной работы
1. Установить наличие
статистической связи между факторным признаком
Х и результативным признаком Y:
а) графическим методом:
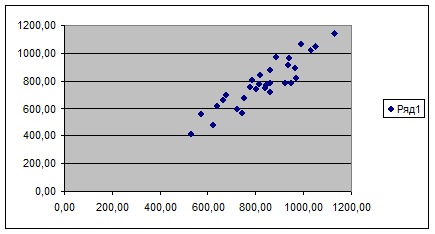
Графический метод состоит в построении
корреляционного поля – множества точек (x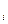 ,y
,y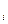 )
в декартовой системе координат (Х,Y).
)
в декартовой системе координат (Х,Y).
По характеру расположения точек
корреляционного поля можно сделать вывод:
1) связь между признаками
сильная, точки группируются тесно;
2) равномерное изменение
значения результативного признакаY,
говорит о наличии прямолинейной корреляционной связи.
б) методом сопоставления параллельных
рядов:
Метод сопоставления взаимосвязанных параллельных рядов является простейшим
приемом обнаружения связи между признаками.
С возрастанием значений признака Х
значения признака Y также в целом возрастают при наличии некоторых
отклонений от этой общей тенденции (Таблица 1в), то между признаками Х и Y
возможно наличие прямой корреляционной связи.
2. Установить наличие
корреляционной связи между признаками Х
и Y методом аналитической группировки:
При переходе от одной группы к другой средние значения ỹ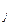 изменяются с определенной закономерностью – возрастают
(Таблица 2), то между признаками Х и Y существует корреляционная
связь.
изменяются с определенной закономерностью – возрастают
(Таблица 2), то между признаками Х и Y существует корреляционная
связь.
3.
Оценить тесноту связи
признаков Х и Y на основе:
а) эмпирического корреляционного
отношения h:
Эмпирическое
корреляционное отношение h = 0,903 (Таблица 4).
б) линейного коэффициента корреляции r.
Линейный коэффициент корреляции r =
0,913 ( Таблица 5).
Значения показателей изменяются в
пределах:
-1≤ r ≤ 1, 0 ≤ η ≤ 1.
Т.к. чем ближе значения показателей к
единице, тем теснее связь и больше сила связи.
Знак при r указывает на направление связи – знак «+»
соответствует прямой линейной зависимости.
По шкале Чэддока значения показателей
тесноты связи r, η лежат в промежутке от 0,9 -0,99, а это
значит весьма высокая связь.
4.
Построить однофакторную
линейную регрессионную модель связи признаков Х
и Y, используя инструмент Регрессия
надстройки Пакет анализа.
Смотреть
Задание 2.
5.
Оценить адекватность и практическую
пригодность построенной линейной регрессионной
модели, указав:
а) доверительные интервалы
коэффициентов а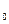 , а
, а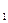 :
:
а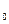 = -121,565, а
= -121,565, а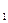 = 1,089
= 1,089
Доверительные интервалы коэффициентов а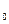 , а
, а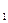 даны в Задание 2.
даны в Задание 2.
б) степень тесноты связи признаков
Х и Y:
Для построенной регрессионной модели
измерение тесноты связи признаков X и Y осуществляется на основе
следующих показателей:
R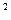 - индекс детерминации равный 0,83;
- индекс детерминации равный 0,83;
R – индекс корреляции равный 0,91;
r - линейный
коэффициент корреляции равный 0,91.
Индекс корреляции R принимает значение в
пределах 0≤ R ≤1, и
близость R к единице означает, что связь между признаками
достаточно хорошо описывается избранным уравнением корреляционной зависимости.
Аналогичные утверждения имеют место и для
линейного коэффициента корреляции r, принимающего значение в пределах -1≤ r ≤ 1.
Пригодность построенной регрессионной модели для практического использования
можно оценить и по величине индекса детерминации R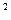 :
неравенству R
:
неравенству R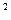 >
0.5 отвечают значения R> 0.7 (или г > 0,7),
что означает высокую степень тесноты связи признаков в уравнении регрессии. При
этом более 50% вариации расчетных значений признака Y объясняется влиянием
фактора Х, что позволяет считать применение синтезированного уравнения
регрессии правомерным.
>
0.5 отвечают значения R> 0.7 (или г > 0,7),
что означает высокую степень тесноты связи признаков в уравнении регрессии. При
этом более 50% вариации расчетных значений признака Y объясняется влиянием
фактора Х, что позволяет считать применение синтезированного уравнения
регрессии правомерным.
6.
Дать экономическую
интерпретацию:
а) коэффициент регрессии а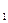 :
:
Коэффициент регрессии, а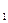 равен 1,089. Величина коэффициента регрессии, а
равен 1,089. Величина коэффициента регрессии, а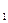 показывает, насколько
в среднем изменяется значение результативного признака Y при изменении фактора Х на
единицу его измерения.
показывает, насколько
в среднем изменяется значение результативного признака Y при изменении фактора Х на
единицу его измерения.
б) коэффициента эластичности К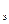 :
:
Коэффициент эластичности К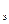 показывает, на сколько
процентов изменяется в среднем результативный признак при изменении факторного
признака на 1%.
показывает, на сколько
процентов изменяется в среднем результативный признак при изменении факторного
признака на 1%.
в) остаточных величин e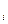 .
.
Анализируя остатки e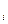 , характеризующие
отклонения i-х наблюдений от значений ŷ
, характеризующие
отклонения i-х наблюдений от значений ŷ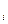 , которые следует
ожидать в среднем, можно сделать ряд практических выводов об эффективности
экономической деятельности рассматриваемых хозяйствующих субъектов и выявить
скрытые резервы их развития и повышения деловой активности. При этом наиболее
значительный экономический интерес
представляют наибольшие и наименьшие
положительные и отрицательные отклонения e
, которые следует
ожидать в среднем, можно сделать ряд практических выводов об эффективности
экономической деятельности рассматриваемых хозяйствующих субъектов и выявить
скрытые резервы их развития и повышения деловой активности. При этом наиболее
значительный экономический интерес
представляют наибольшие и наименьшие
положительные и отрицательные отклонения e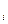 .
.
7.
Найти наиболее адекватное
нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм.
Построить для этого уравнения теоретическую кривую регрессии.
Построение наиболее адекватного уравнения регрессии
представлено на Диаграмме 2.