Задача 1
Условие
Анализ 10% банковских счетов населения региона, выделенных в
результате бесповторного собственно-случайного отбора показал следующее
распределение:
|
Размер вклада, тыс. руб.
|
Количество вкладов, %
|
|
До 1,0
|
20,0
|
|
1,0-5,0
|
25,0
|
|
5,0-10,0
|
40,0
|
|
10,0-15,0
|
10,0
|
|
15,0 и более
|
5,0
|
Определите:
1.
Средний размер вклада
2.
С вероятностью Р=0,954, установите пределы для всей
совокупности вкладов населения
А) среднего
размера вклада
Б) доли вкладов
до 5 тыс. руб.
В) общей суммы
вкладов
Решение
1. Определим средний
размер вклада
|
Размер вклада, тыс. руб.
|
Количество вкладов, %
|
Xj
|
XiFi
|
|
До 1,0
|
20
|
0,5
|
10
|
|
1,0-5,0
|
25
|
3
|
75
|
|
5,0-10,0
|
40
|
7,5
|
300
|
|
10,0-15,0
|
10
|
12,5
|
125
|
|
15,0 и более
|
5
|
17,5
|
87,5
|
|
Итого
|
100
|
41
|
597,5
|
Средний размер
вклада определяется по формуле
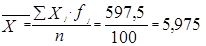
2. С
вероятностью Р=0,954, установим пределы для всей совокупности вкладов населения
среднего размера вклада
|
Размер
вклада, тыс. руб.
|
Количество
вкладов, %
|
Xj
|
Xi * Fj
|
xi2Fj
|
| Xj -X |
|
| Xj - X | * Fi
|
|
До
1,0
|
20
|
0,5
|
10
|
5
|
5,475
|
599,51
|
|
1,0-5,0
|
25
|
3
|
75
|
225
|
2,975
|
221,27
|
|
5,0-10,0
|
40
|
7,5
|
300
|
2250
|
1,525
|
93,03
|
|
10,0-15,0
|
10
|
12,5
|
125
|
1562,5
|
6,525
|
425,76
|
|
15,0
и более
|
5
|
17,5
|
87,5
|
1531,25
|
11,525
|
664,13
|
|
Итого
|
100
|
41
|
597,5
|
5573,75
|
28,025
|
2003,7
|
Для определения пределов в необходимо найти дисперсию выборочной
совокупности:
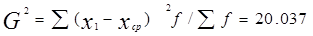
Р = 0,954, t=2
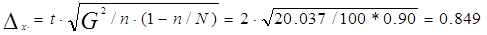
Пределы средней генеральной
минимальный: 5,975-0,849=5,126
Максимальный: 5,975+0,849=6,824
С вероятностью
Р=0,954, установим пределы для всей совокупности вкладов населения доли вкладов
до 5 тыс. руб.
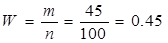
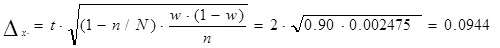
Пределы доли выборки
минимальный: 0,45-0,0944=0,3556
Максимальный: 0,45+0,0944=0,5444
Задача №2
Условие
Имеются данные о потерях рабочего времени на предприятии
следствии заболеваемости с временной утратой трудоспособности:
|
Год
|
Потери времени, чел-дни
|
|
1
|
933,4
|
|
2
|
904,0
|
|
3
|
965,0
|
|
4
|
1014,1
|
|
5
|
1064,8
|
|
6
|
1122,9
|
1. Для определения тенденции изменения потерь рабочего
времени подберите вид аналитической функции
2. Отобразите фактические и теоретические уровни ряда на
графике. Покажите ожидаемые урони ряда на следующие 2-3 года. Сделайте выводы
Решение
Для решения сперва определим средний абсолютный прирост
|
Год
|
Потери
времени, чел-дни
|
Абсолютный
прирост
|
|
1
|
933,4
|
0
|
|
2
|
904
|
-29,4
|
|
3
|
965
|
61
|
|
4
|
1014,1
|
49,1
|
|
5
|
1064,8
|
50,7
|
|
6
|
1122,9
|
58,1
|
|
Средний абсолютный прирост
|
37,9
|
Функция F=Х+37.9,
где
Х – базисное значение
n – число лет
Далее рассчитаем потери на 7,8,9 годы
7 год –
1160,8
8 год –
1198,7
9 год -
1239,6
Теперь построим график
Как видно
из графика лини выровненного ряда близка с фактическому, что означает верность
подобранной функции
Задача №3
Условие
Имеются данные по предприятиям отрасли
|
Предприятия
|
Стоимость
ОФ
|
Прибыль,
тыс. руб.
|
|
Предыдущий
год
|
Отчетный
год
|
Предыдущий
год
|
Отчетный
год
|
|
1
|
10000
|
12500
|
2000
|
2400
|
|
2
|
7400
|
7800
|
1560
|
1820
|
Определите
1.
Индексы рентабельности для каждого предприятия в
отдельности
2.
Индексы рентабельности производства:
а) переменного
состава
б) постоянного
состава
в) структурных
сдвигов
Покажите
взаимосвязь индексов.
Решение
Рентабельность
производства (прибыль / стоимость ОПФ)
|
предприятие
|
Предыдущий год
|
Отчетный год
|
|
1
|
0,200
|
0,192
|
|
2
|
0,211
|
0,233
|
Индекс
рентабельности производства
1 предприятие:
0,192 / 0,200 = 0,960
2 предприятие:
0,233 / 0,211 = 1,104
Индекс
постоянного состава:
I пост = ((2400+1820)/(
10000+7400)) / ((2000+1560) / (10000+7400)) = 0,2425 / 0,2046 = 1,1854
Индекс
переменного состава:
I пер
=((2400+1820)/(12500+7800)) / ((2000+1560)/(10000+7400))=0,2079 / 0,2046 =
1,016
Индекс
структурных сдвигов:
I стр = Iпост / I пер = 1,1854 / 1,016 = 1,167
Задача №4
Условие
Оцените тесноту
связи признаков
|
Работа со
свинцом
|
Обследовано
рабочих, чел
|
|
Всего
|
В том
числе
|
|
Больные
онкологические
|
Здоровые
|
|
Да
|
36
|
28
|
8
|
|
Нет
|
144
|
62
|
82
|
|
Итого
|
180
|
90
|
90
|
Решение
Для определения тесноты связи используем коэффициент
ассоциации и контингенции
Таблица
сопряженности (условные обозначения)
|
Больные
|
Здоровые
|
Итого
|
|
a
|
b
|
a+b
|
|
c
|
d
|
c+d
|
|
a+c
|
b+d
|
a+b+c+d
|
Коэффициент ассоциации:
Ка =
(ad-bc) / (ad + bc) = (2296-496) / (2296+496)
= 1800 / 2792 =0,645
Коэффициент контингенции:
Kk =
(ad-bc) / Ö(a+b)(b+d)(a+c)(c+d)=1800 / Ö(36*90*90*144)=1800 / 6480 = 0.277
Коэффициент ассоциации больше 0,5, а коэффициент
контингенции меньше 0,3, Следовательно, связь не может считаться подтвержденной.
Задача №5
Условие
Имеются следующие данные по экономике страны (млрд. руб.)
|
Наименование показателя
|
Значение
|
|
Выпуск продуктов в основных ценах
|
3900
|
|
Выпуск рыночных услуг (за
исключением условно исчисленных услуг финансовых посредников)
|
1100
|
|
Выпуск не рыночных услуг
|
900
|
|
Налоги на продукты и услуги
|
790
|
|
Прочие косвенные налоги
|
310
|
|
Экспорт товаров и услуг
|
430
|
|
Импорт товаров и услуг
|
350
|
|
Проценты, полученные банками по
ссудам
|
290
|
|
Проценты, уплаченные банками за
пользование денежными средствами
|
165
|
|
Субсидии на импорт
|
45
|
|
Материальные затраты на
производство продуктов и услуг в течении года:
|
2175
|
|
- износ ОС
- недоамортизированная стоимость
выбывших ОС
|
405
45
|
|
Прочие элементы промежуточного
потребления
|
90
|
Определите валовой внутренний продукт в рыночных ценах
Решение
ВВП = SВВ - SПП+SЧН
SВВ
= 3900+1100+900+(350-290) = 5960
SПП
= 405+45+90+2175=2715
SЧН
= 790+350-45=1095
ВВП = 5960-2715+1095=4340 млрд. руб.
Задача №6
Условие
Имеются следующие данные о распределении населения региона
по 10% группам по уровню среднедушевого дохода:
|
Базисный
|
Отчетный
|
|
Первая
|
2,3
|
2,1
|
|
Вторая
|
3,7
|
3,3
|
|
Третья
|
5,2
|
4,2
|
|
Четвертая
|
6,4
|
5,8
|
|
Пятая
|
7,6
|
7,2
|
|
Шестая
|
10,0
|
8,9
|
|
Седьмая
|
12,2
|
8,9
|
|
Восьмая
|
14,3
|
12,5
|
|
Девятая
|
16,7
|
21,4
|
|
Десятая
|
21,6
|
25,7
|
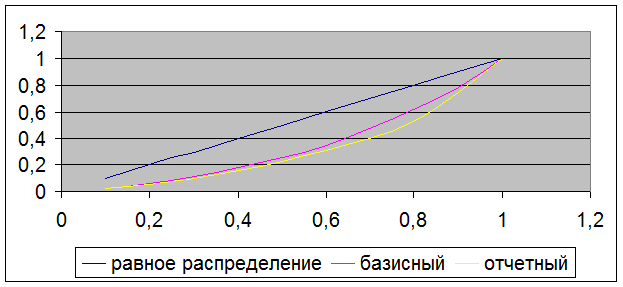
Определить коэффициенты концентрации доходов Джинни.
Построить график Лоренца. Сделать выводы
Решение
Для определения коэффициенты концентрации доходов Джинни
необходимо произвести ряд дополнительных расчетов:
|
Доля в совокупном доходе страны
|
Расчетные показатели
|
|
|
Базисный период
|
Отчетный период
|
|
X1
|
SumX1
|
Базис.
|
Отчет.
|
SumY0
|
X1Y0
|
SumY0X1
|
SumY1
|
X1Y1
|
SumY1X1
|
|
0,1
|
0,1
|
0,023
|
0,021
|
0,023
|
0,0023
|
0,0023
|
0,021
|
0,0021
|
0,0021
|
|
0,1
|
0,2
|
0,037
|
0,033
|
0,06
|
0,0037
|
0,006
|
0,054
|
0,0033
|
0,0054
|
|
0,1
|
0,3
|
0,052
|
0,042
|
0,112
|
0,0052
|
0,0112
|
0,096
|
0,0042
|
0,0096
|
|
0,1
|
0,4
|
0,064
|
0,058
|
0,176
|
0,0064
|
0,0176
|
0,154
|
0,0058
|
0,0154
|
|
0,1
|
0,5
|
00,76
|
0,072
|
0,252
|
0,0076
|
0,0252
|
0,226
|
0,0072
|
0,0226
|
|
0,1
|
0,6
|
0,100
|
0,089
|
0,352
|
0,01
|
0,0352
|
0,315
|
0,0089
|
0,0315
|
|
0,1
|
0,7
|
0,122
|
0,089
|
0,474
|
0,0122
|
0,0474
|
0,404
|
0,0089
|
0,0404
|
|
0,1
|
0,8
|
0,143
|
0,125
|
0,617
|
0,0143
|
0,0617
|
0,529
|
0,0125
|
0,0529
|
|
0,1
|
0,9
|
0,167
|
0,214
|
0,784
|
0,0167
|
0,0784
|
0,743
|
0,0214
|
0,0743
|
|
0,1
|
1,0
|
0,216
|
0,257
|
1,000
|
0,0216
|
0,1
|
1,000
|
0,0257
|
0,1
|
|
1,0
|
|
1,000
|
1,000
|
|
0,1
|
0,385
|
|
0,100
|
0,354
|
G=1-2*å
SumYX + åYX
Для базисного периода:
1-2*0,385+0,1 = 0,33
Для отчетного периода:
1-2*0,354+0,1=0,392
Расслоение населения по уровню дохода за рассматриваемый
период возросло, поскольку отклонение кривой Лоренца от линии равномерного
распределения изменилась в сторону увеличения площади образованной этой кривой
и линией равномерного распределения.
В отчетном периоде коэффициент Джинни ближе к единице,
следовательно выше уровень неравенства по доходу.
Задание №7
Условие
Предприятие работает с 25 сентября
. Численность работников списочного состава была следующей:
25 сентября – 180 чел, 26 сентября – 185 чел, 27 сентября – 200 чел, 28
сентября – 210 чел. 29 и 30 сентября - выходные
Кроме того известно,
что число совместителей с 25 по 27 сентября – 5 чел., с 28 по 30 сентября – 7
чел, а число работающих по договорам
гражданско-правового характера – с 25.09 по 27.09 – 10 чел, с 28 по
30.09 – 12 чел. Среднесписочная численность за октябрь – 180 чел, ноябрь – 175
чел. В декабре число неявок на работу составили 3960 человеко-дней, число
неявок по всем причинам 1800 человек-дней.
Определите среднесписочную численность за год.