Задание 1.
Составить математическую модель преобразования ресурсов предприятия в
продукцию или услуги.
1.
Исходные данные представляем в виде таблицы:
Наименование
продукции
(объем – хi)
|
Наименование материалов и ресурсов (объем – уi)
|
|
Количество ткани, м.
|
Стоимость
фурнитуры, руб.
|
Стоимость
пошива, руб.
|
|
Блузка
|
2
|
50
|
200
|
|
Юбка
|
1
|
30
|
100
|
|
Брюки
|
1,4
|
50
|
150
|
2.
Записать математическую модель в виде системы
линейных алгебраических уравнений и векторно-матричной форме у=Ах, где у, х –
векторы, А – матрица соответствующей размерности, элементы которой равны нормам
расхода.
Пусть 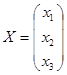 - вектор объема
продукции,
- вектор объема
продукции,  - вектор объема ресурсов,
- вектор объема ресурсов, 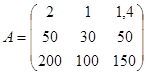 - матрица, элементы которой равны нормам расхода. Тогда
математическую модель можно записать в виде системы линейных алгебраических
уравнений:
- матрица, элементы которой равны нормам расхода. Тогда
математическую модель можно записать в виде системы линейных алгебраических
уравнений: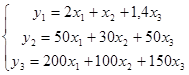 или в
векторно-матричной форме:
или в
векторно-матричной форме: 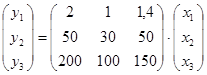 .
.
3.
Решить прямую задачу: при известных (планируемых)
значениях объемов хi продукции
или услуг определить необходимое количество уi материалов и ресурсов (решить
уравнение у=Ах).
Пусть планируются объемы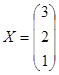 . Находим необходимое количество материалов и ресурсов:
. Находим необходимое количество материалов и ресурсов: 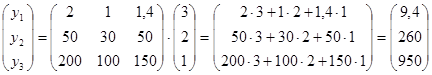
4.
Решить обратную задачу: при заданных (ограничениях)
значениях количества уi материалов
и ресурсов определить возможные значения объемов хi продукции
или услуг (решить уравнение х=А-1у).
Пусть заданы значения количества материалов и ресурсов 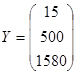 .
.
Определим возможные значения объемов продукции. Для
этого решаем уравнение х=А-1у. Находим матрицу А-1 по
формуле 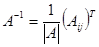 .
.
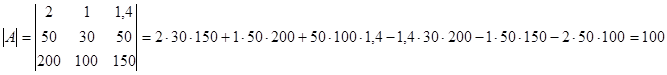
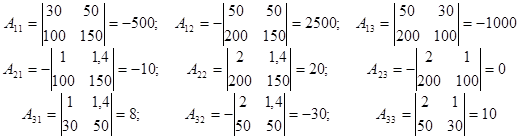
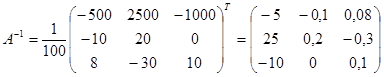 .
.
Получаем возможные значения
объемов продукции

Задание 2.
Решить задачу оптимального планирования производства.
1. Исходные данные процесса производства (преобразования ресурсов
предприятия) продукции или услуг формируются в виде таблицы:
|
Наименование
продукции
(хi)
|
Наименование материалов или ресурсов
|
Прибыль
на единицу
продукции
|
|
Ткань,
м.
|
Пуговицы,
шт.
|
Молнии,
шт.
|
Время изго-
товления, ч.
|
|
Блузка
|
2
|
8
|
3
|
3
|
250
|
|
Юбка
|
1
|
2
|
1
|
2
|
100
|
|
Фонд
материалов
или ресурсов
|
13
|
60
|
16
|
24
|
|
2. Составить систему алгебраических неравенств вида Sаiхi£bi,
отражающих ограничения на необходимые материалы или ресурсы при изготовлении
продукции (или предоставления услуг).
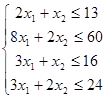
3. Составить целевую функцию вида J=Scixi ,
отражающую суммарную прибыль при реализации общего количества изделий (или
услуг) или затраты на их производство.
Суммарная
прибыль:

4. Сформулировать задачу линейного программирования в текстовой форме.
Найти
значения х1, х2, удовлетворяющие ограничениям
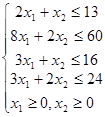
и доставляющие максимальное значение функции прибыли
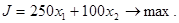
5.
 Решить
задачу линейного программирования с определением целевой функции в вершинах
многогранника на плоскости в пространстве двух переменных. Данные расчетов
целевой функции представить в виде таблицы.
Решить
задачу линейного программирования с определением целевой функции в вершинах
многогранника на плоскости в пространстве двух переменных. Данные расчетов
целевой функции представить в виде таблицы.
Строим
прямые:
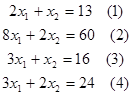
Областью
допустимых значений является многоугольник ОАВСD.
|
Индекс
вершины
|
Координаты вершины
|
Значение целевой
функции
|
|
Х1
|
Х2
|
|
А
|
0
|
12
|
1200
|
|
В
|
2
|
9
|
1400
|
|
С
|
3
|
7
|
1450
|
D
|
5,33
|
0
|
1325,5
|
6.
Определить значения Х1 и Х2, при
которых целевая функция равна максимальному значению (в случае прибыли) или
минимальному значению (в случае затрат).
Целевая функция равна
максимальному значению в точке С(3;7).
Таким образом, Х1 =
3, Х2 = 7.