Задача
6.
Преподаватели кафедры Прикладной информатики
преподают на трех факультетах: механическом, технологическом, экономическом. На
технологическом работает 22
преподавателя, на механическом – 23, на механическом или экономическом – 36.
Только на технологическом – 10 преподавателей; 2 – на трех факультетах. Только
на механическом и экономическом факультетах – 5 преподавателей. Число
преподавателей, работающих только на механическом и технологическом
факультетах, равно числу преподавателей, работающих на экономическом и
технологическом факультетах. Сколько преподавателей работает на кафедре?
Решение.
Обозначим через
МВ – количество всех
преподавателей кафедры Прикладной информатики;
Мм – количество преподавателей, работающих только на
механическом факультете;
МТ – количество преподавателей, работающих только на
технологическом факультете;
МЭ – количество преподавателей,
работающих только на экономическом факультете;
ММТ – количество преподавателей,
работающих только на двух факультетах: механическом и технологическом;
ММЭ – количество преподавателей,
работающих только на двух факультетах: механическом и экономическом;
МТЭ – количество преподавателей,
работающих только на двух факультетах: технологическом и экономическом;
ММТЭ – количество преподавателей,
работающих на трех факультетах.
По условию
задачи, так как на
механическом или экономическом
факультетах работают 36
человек, получаем:
ММ
+ МЭ + ММТ + ММЭ + МТЭ + ММТЭ
= 36 (условие 1).
Так как только на технологическом факультете работают 10 преподавателей, то
МТ
= 10 (условие 2).
Требуется
найти МВ.
Диаграмма Эйлера-Вена:
Из
диаграммы Эйлера-Вена получаем:
МВ
= ММ + МЭ + МТ + ММТ + ММЭ
+ МТЭ + ММТЭ.
По условию
1: ММ + МЭ + ММТ + ММЭ + МТЭ
+ ММТЭ = 36.
По условию
2: МТ = 10.
Получаем: МВ
= 36 + 10 = 46.
Ответ: 46
преподавателей работает на кафедре
Прикладной информатики.
Задача 16.
Если все посылки истинны и аргумент – правильный, то
заключение истинно. Заключение ложно. Следовательно, аргумент неправильный или
не все посылки истинны.
Решение.
Обозначим
высказывания:
А – «посылки истинны»;
В – «аргумент
правильный»;
С – «заключение истинно».
Данное
рассуждение можно представить в виде формулы:
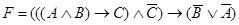 .
.
Проверим
формулу на тождественную истинность.
Введем
обозначения:
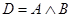 ;
;
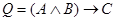 ;
;
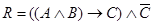 ;
;
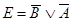 .
.
Составляем
таблицу истинности:
|
А
|
B
|
C
|
D
|
Q
|
R
|
E
|
F
|
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
Так как формула F
является тождественно истинной, данное рассуждение верно.
Задача 26.
По
заданной функции проводимости построить СКНФ и СДНФ. Упростить полученные
формулы:
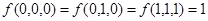 .
.
Решение.
Исходя из условия, построим таблицу истинности
заданной функции проводимости:
|
х
|
y
|
z
|
f(x,y,z)
|
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
По наборам, на которых функция равна 1, строим СДНФ:
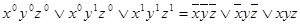 .
.
По
наборам, на которых функция равна 0, строим СКНФ:
 .
.
Упростим
СДНФ:
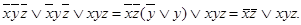 .
.
Для проверки равносильности составим таблицу
истинности полученной формулы.
|
х
|
y
|
z
|
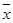
|
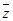
|
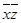
|
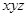
|
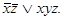
|
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
Так как таблицы истинности совпадают, формулы
равносильны.
Упростим
СКНФ:
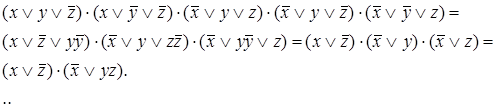
Для
проверки равносильности составим таблицу истинности полученной формулы.
|
х
|
y
|
z
|
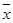
|
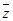
|
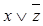
|
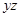
|
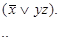
|
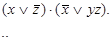
|
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
|
0
|
1
|
0
|
0
|
0
|
|
1
|
1
|
0
|
|
1
|
1
|
0
|
0
|
0
|
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
.
Так как таблицы истинности совпадают, формулы равносильны.
Литература.
1.
Информатика. Учебник/ Под ред. проф. Н.В.Макаровой.
– М.: Финансы статистика, 1997.
2.
Информатика и математика и для юристов: Учеб.
пособие для вузов/ Под ред. проф.
Х.А.Андриашина, проф. С.Я. Казанцева. – М.: ЮНИТИ-ДАНА, Закон и право, 2001.
3.
Богатов Д.Ф., Богатов Ф.Г. Основы информатики
и математики для юристов: Учеб. пособие. В 2-х томах. М.: ПРИОР, 2000.