Вариант 4.
1)
С помощью кругов Эйлера проверьте, является ли
силлогизм АAA
правильным по второй фигуре.
Решение.
Силлогизм
ААА построенный по второй фигуре имеет вид:
|
Все М суть Р
|
А
|
|
Все S
суть Р
|
А
|
|
Все М суть S
|
А
|
Строим
круги Эйлера для этого умозаключения:
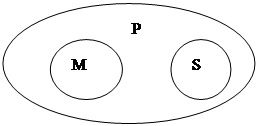
Заключаем,
что силлогизм АAA не
является правильным по первой фигуре.
2).Методом
от противного проверьте, является ли следующая формула законом? 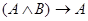 .
.
Решение.
Формула 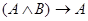 является законом
тогда и только тогда, когда формула
является законом
тогда и только тогда, когда формула 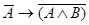 является законом.
является законом.
Составляем
таблицу истинности формулы 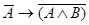 :
:
|
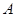
|
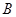
|
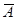
|
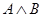
|
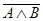
|
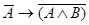
|
|
0
|
0
|
1
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
0
|
1
|
Так как
формула 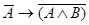 на всех наборах равна
1, то формула
на всех наборах равна
1, то формула 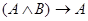 является законом.
является законом.
3)
Определите, верно ли произведена операция обобщения
понятия:
Староста группы – староста курса.
Решение.
Так как
староста группы не является старостой
курса, то операция обобщения понятия произведена неверно.
4)
Постройте отрицание для суждения:
Иванов и
Сидоров шахматисты.
Решение.
Отрицанием
данного суждения является суждение:
Иванов
или Сидоров не являются шахматистами.
5)
Осуществите превращение суждения:
Некоторые
школьники являются баскетболистами.
Решение.
В
результате превращения получаем суждение:
Некоторые
школьники не являются не баскетболистами.