Вариант 6.

1)               Находятся ли суждения в отношении логического следования? 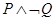 и .

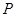Решение.

Составим таблицу истинности формулы :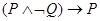

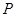
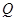
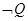
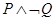
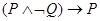
0	0	1	0	1
0	1	0	0	1
1	0	1	1	1
1	1	0	0	1

Так как формула 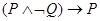 на всех наборах равна 1, то вторая формула  является логическим следствием первой.

Составим таблицу истинности формулы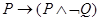

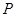
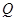
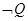
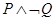
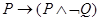
0	0	1	0	1
0	1	0	0	1
1	0	1	1	1
1	1	0	0	0

Так как формула 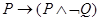не на всех наборах равна 1, то первая формула не является логическим следствием второй.

2)               С помощью таблиц проверьте, является ли следующее суждение законом? .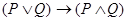

Решение.

Составляем таблицу истинности:

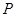
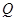
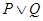
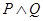
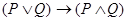
0	0	0	0	1
0	1	1	0	0
1	0	1	0	0
1	1	1	1	1

Так как формула не на всех наборах равна 1, то суждение не является законом.

3)               По логическому квадрату, проверить в каком отношении находятся суждения.

Все медведи хищники. Некоторые медведи хищники.

Решение.

Суждение «Все медведи хищники» является общеутвердительным (тип А). Суждение «Некоторые медведи хищники» является частноутвердительным (тип I). По логическому квадрату второе суждение находятся  в подчинении первому.

4) Методом от противного проверьте, является ли следующая формула законом? .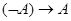

Решение. Формула 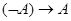  является законом тогда и только тогда, когда формула 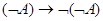 является законом.

Составляем таблицу истинности формулы :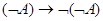

0	1	0	0
1	0	1	1

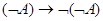Так как формула  не на всех наборах равна 1, то формула 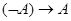  не является законом.

5)    Осуществите превращение непосредственного силлогизма:

Некоторые вороны являются черными.

Решение.

В результате превращения получаем суждение:

Некоторые вороны не являются не черными.