Содержание:
1. Задание №1: «Определение рыночной
стоимости облигации» стр.1
2. Задание №2: «Распределение
инвестиций»
стр.3
3. Задание №3: «По погашению
задолженности по частям» стр.6
4. Список литературы стр.8
Задание №1: «Определение рыночной
стоимости облигации»
Постановка задачи:
Номинальная стоимость
облигации 9000 руб. выпускается сроком на 15 лет. Держатель облигации ежегодно
получает 13% ежегодных доходов. Банковская ставка в момент выпуска облигации – 10%.
Но через 5 лет действия облигации банковская ставка увеличивается до 20%.
Задание:
1. Определить рыночную
стоимость облигации в течение всего периода ее действия.
2. Построить график
изменения рыночной стоимости.
3. Алгоритм решения.
4. Вывод.
Решение:
1. Стоимость облигации в любой
момент времени t=0,1,...,n рассчитывается по формуле:
CO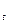 = Y * 1-(1+j)
= Y * 1-(1+j)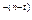 + _S___
+ _S___
j (1+j)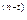 ,
,
где
CO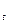 - Стоимость облигации в момент времени t
- Стоимость облигации в момент времени t
j - Банковская ставка (десятичная дробь)
t - Момент времени
n - Cрок действия облигации (кол-во лет)
S - Номинал облигации
Y - Ежегодный доход, определяется по
проценту на купоне.
Используя Excel формулу вычисления стоимости облигации
можно разложить на составляющие, тогда формула примет следующий вид:
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
|
1
|
t
|
n-A
|
j
|
1+C
|
D^B
|
1/E
|
(1-F)/C
|
Y*G
|
S/E
|
H+I
|
Таблица 1
Определение
рыночной стоимости облигации
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
|
1
|
t
|
n-A
|
j
|
1+C
|
D^B
|
1/E
|
(1-F)/C
|
Y*G
|
S/E
|
H+I
|
|
2
|
0
|
15
|
0,1
|
1,1
|
4,177248
|
0,239392
|
7,60608
|
8899,113
|
2154,528
|
11053,64
|
|
3
|
1
|
14
|
0,1
|
1,1
|
3,797498
|
0,263331
|
7,366687
|
8619,024
|
2369,981
|
10989,01
|
|
4
|
2
|
13
|
0,1
|
1,1
|
3,452271
|
0,289664
|
7,103356
|
8310,927
|
2606,979
|
10917,91
|
|
5
|
3
|
12
|
0,1
|
1,1
|
3,138428
|
0,318631
|
6,813692
|
7972,019
|
2867,677
|
10839,7
|
|
6
|
4
|
11
|
0,2
|
1,2
|
7,430084
|
0,134588
|
4,32706
|
5062,66
|
1211,292
|
6273,952
|
|
7
|
5
|
10
|
0,2
|
1,2
|
6,191736
|
0,161506
|
4,192472
|
4905,192
|
1453,55
|
6358,743
|
|
8
|
6
|
9
|
0,2
|
1,2
|
5,15978
|
0,193807
|
4,030967
|
4716,231
|
1744,26
|
6460,491
|
|
9
|
7
|
8
|
0,2
|
1,2
|
4,299817
|
0,232568
|
3,83716
|
4489,477
|
2093,112
|
6582,589
|
|
10
|
8
|
7
|
0,2
|
1,2
|
3,583181
|
0,279082
|
3,604592
|
4217,372
|
2511,735
|
6729,107
|
|
11
|
9
|
6
|
0,2
|
1,2
|
2,985984
|
0,334898
|
3,32551
|
3890,847
|
3014,082
|
6904,929
|
|
12
|
10
|
5
|
0,2
|
1,2
|
2,48832
|
0,401878
|
2,990612
|
3499,016
|
3616,898
|
7115,914
|
|
13
|
11
|
4
|
0,2
|
1,2
|
2,0736
|
0,482253
|
2,588735
|
3028,819
|
4340,278
|
7369,097
|
|
14
|
12
|
3
|
0,2
|
1,2
|
1,728
|
0,578704
|
2,106481
|
2464,583
|
5208,333
|
7672,917
|
|
15
|
13
|
2
|
0,2
|
1,2
|
1,44
|
0,694444
|
1,527778
|
1787,5
|
6250
|
8037,5
|
|
16
|
14
|
1
|
0,2
|
1,2
|
1,2
|
0,833333
|
0,833333
|
975
|
7500
|
8475
|
|
17
|
15
|
0
|
0,2
|
1,2
|
1
|
1
|
0
|
0
|
9000
|
9000
|
В таблице 1 представлено решение в Excel по определению рыночной стоимости
облигации с помощью составляющих. Значения
столбца J характеризуют рыночную стоимость облигации по годам с момента
выпуска.
2. График изменения
рыночной стоимости строится с помощью «Мастер Диаграмм».
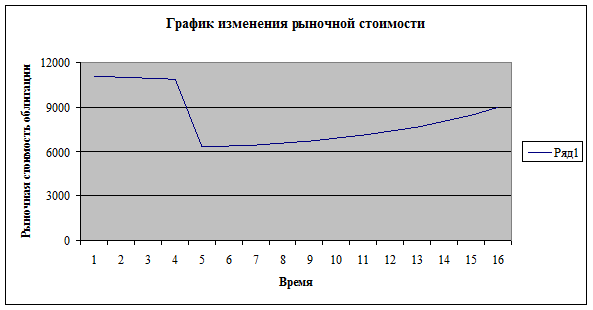
Рис.1
Изменение рыночной стоимости облигации
3. Алгоритм решения:
А1 = t = момент
времени
В1 = n-A = (n-t) срок действия облигации на момент времени t
С1 = j
= банковская ставка (с
учетом изменения банковской ставки в определенный момент времени)
D1 = 1+C = начисление %
E1 = D^B = (1+j) 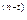
F1 = 1/E = (1+j)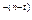
G1 = (1-F)/C = 1-(1+j)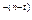
j
H1 = Y*G =
Y * 1-(1+j)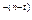
j
I1 = S/E = _S__
(1+j)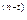
J1 = H+I = CO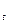 = Y * 1-(1+j)
= Y * 1-(1+j)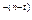 + _S___
+ _S___
j (1+j)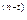
4. Вывод.
Если процент по облигации
больше банковской ставки, то рыночная стоимость облигации выше номинала и
постепенно уменьшается и к концу срока становится равной номиналу. Но если
стоимость облигации падает, но в какой то момент времени банковская ставка растет,
то стоимость облигации падает, а затем растет. (Рис.1)
Задание №2: «Распределение
инвестиций»
Постановка задачи:
Имеются два проекта А и
В. Проект А гарантирует 70 коп прибыли на вложенный 1 рубль через 1 год. Проект
В – 160 коп прибыли на вложенный 1 рубль через 2 года.
Задача: Как управлять капиталом в 14000 руб., т.е. вложить в проект А или В, что
бы капитал был максимальным через 4 года.
Задание.
1. Составить модель
линейного программирования.
2. Используя средство «Поиск
решения» в Excel найти
оптимальный план распределение капитала по проектам.
3. Найти границы
эффективности проектов, при которых вложения в проект А меняется на вложения в
проект В и наоборот.
4. Алгоритм решения.
5. Вывод.
Решение:
1. Составим модель
линейного программирования:
Целевая функция: 1,70 Х4А
+ 2,60 Х3В → maх
Таблица 2.1
Модель
линейного программирования в Excel
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
К
|
L
|
|
1
|
|
|
|
|
переменные
|
|
|
|
|
|
|
|
|
2
|
|
X1А
|
Х1В
|
Х2А
|
Х2В
|
Х3А
|
Х3В
|
Х4А
|
Х4В
|
|
|
|
|
3
|
значение
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
ЦФ
|
|
|
|
4
|
коэф.ЦФ
|
0
|
0
|
0
|
0
|
0
|
2,6
|
1,7
|
0
|
0
|
|
|
|
5
|
|
|
|
|
Ограничения
|
|
|
|
|
лев часть
|
знак
|
прав часть
|
|
6
|
1 год
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
<=
|
14000
|
|
7
|
2 год
|
-1,7
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
<=
|
0
|
|
8
|
3 год
|
0
|
-2,6
|
-1,7
|
0
|
1
|
1
|
0
|
0
|
0
|
<=
|
0
|
|
9
|
4 год
|
|
|
|
-2,6
|
-1,7
|
0
|
1
|
1
|
0
|
<=
|
0
|
2. Используя средство «Поиск
решения» в Excel найдем
оптимальный план распределения капитала по проектам.
Таблица 2.2
Оптимальный
план распределения капитала
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
К
|
L
|
|
1
|
|
|
|
|
переменные
|
|
|
|
|
|
|
|
|
2
|
|
X1А
|
Х1В
|
Х2А
|
Х2В
|
Х3А
|
Х3В
|
Х4А
|
Х4В
|
|
|
|
|
3
|
значение
|
14000
|
0
|
23800
|
0
|
40460
|
0
|
68782
|
0
|
ЦФ
|
|
|
|
4
|
коэф.ЦФ
|
0
|
0
|
0
|
0
|
0
|
2,6
|
1,7
|
0
|
116929,4
|
|
|
|
5
|
|
|
|
|
Ограничения
|
|
|
|
|
лев часть
|
знак
|
прав часть
|
|
6
|
1 год
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
14000
|
<=
|
14000
|
|
7
|
2 год
|
-1,7
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
<=
|
0
|
|
8
|
3 год
|
0
|
-2,6
|
-1,7
|
0
|
1
|
1
|
0
|
0
|
0
|
<=
|
0
|
|
9
|
4 год
|
|
|
|
-2,6
|
-1,7
|
0
|
1
|
1
|
0
|
<=
|
0
|
3. Границы эффективности.
Таблица 2.3
Эффективность
проекта.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
К
|
L
|
|
1
|
|
|
|
|
переменные
|
|
|
|
|
|
|
|
|
2
|
|
X1А
|
Х1В
|
Х2А
|
Х2В
|
Х3А
|
Х3В
|
Х4А
|
Х4В
|
|
|
|
|
3
|
значение
|
0
|
14000
|
0
|
0
|
0
|
40460
|
0
|
0
|
ЦФ
|
|
|
|
4
|
коэф.ЦФ
|
0
|
0
|
0
|
0
|
0
|
2,89
|
1,7
|
0
|
116929,4
|
|
|
|
5
|
|
|
|
|
Ограничения
|
|
|
|
|
лев
часть
|
знак
|
прав
часть
|
|
6
|
1
год
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
14000
|
<=
|
14000
|
|
7
|
2
год
|
-1,7
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
<=
|
0
|
|
8
|
3
год
|
0
|
-2,89
|
-1,7
|
0
|
1
|
1
|
0
|
0
|
0
|
<=
|
0
|
|
9
|
4
год
|
|
|
|
-2,89
|
-1,7
|
0
|
1
|
1
|
0
|
<=
|
0
|
4. Алгоритм решения:
В Excel для нахождения оптимального плана
распределения капитала по проектам заносим следующие формулы:
В ячейке J4: СУММПРОИЗВ(B$3:I$3;B4:I4)
В ячейке J6: СУММПРОИЗВ(B$3:I$3;B6:I6)
В ячейке J7: СУММПРОИЗВ(B$3:I$3;B7:I7)
В ячейке J8: СУММПРОИЗВ(B$3:I$3;B8:I8)
В ячейке J9: СУММПРОИЗВ(B$3:I$3;B9:I9)
После заполнения таблицы: «Сервис» – «Поиск
решения»:
- «Установить целевую ячейку» - «$J$4»
- «Изменяя ячейки» - «B$3:I$3»
- «Добавление ограничения» -
$J$6 <= $L$6
$J$7 <= $L$7
$J$8 <= $L$8
$J$9 <= $L$9
- «Параметры» - активируем
окна «Линейная модель и «Неотрицательные значения» - «ОК»- «Выполнить».
5. Вывод.
Банк В будет эффективным,
если гарантирует 189 коп прибыли на вложенный рубль, вместо 160 коп. (табл. 2.3).
Задание №3: «По погашению задолженности
по частям»
Постановка задачи:
Имеется обязательство
погасить долг в размере 41000 руб. за период с 07.01.2008г. по 10.10.2008г. Кредитор
согласен получать частичные платежи. Процентная ставка 25%. График поступления
частичных платежей:
|
Дата поступления
|
Величина (руб.)
|
|
18.02.2008г.
|
900
|
|
26.03.2008г.
|
1400
|
|
19.04.2008г.
|
500
|
|
25.05.2008г.
|
830
|
|
5.06.2008г.
|
1100
|
|
28.07.2008г.
|
1500
|
|
15.08.2008г.
|
170
|
|
11.09.2008г.
|
900
|
Задание:
1. Используя табличный
процессор Excel определить остаток долга на момент погашения, используя актуарный метод.
2. Алгоритм решения.
3. Вывод.
Решение:
1. Актуарный метод –
поступивший платеж идет в первую очередь на погашение процентов, начисленных на
дату платежа, а остаток платежа идет на погашение основного долга, если
поступивший платеж меньше процентов, то никаких зачетов не производится, и этот
платеж добавляется к следующему платежу.
Таблица 3.1
Расчет
остатка долга на момент погашения
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
Н
|
|
1
|
Исходные данные
долг + %
|
Момент открытия
кредита. Дни поступления платежей и дата погашения
|
Кол-во дней между
поступлением
платежей
|
Велич
ина плате
жа
|
Кол-во дней от
послед
него списания
долга (суммируются дни, если нет списания)
|
Накопленные
платежи (суммируются платежи, если они меньше %)
|
Остаток долга
после поступления платежа
|
Процент
|
|
2
|
кредит
41000
|
07.01.08
|
|
|
|
|
41000,00
|
|
|
3
|
проценты
25 %
|
18.02.08
|
41
|
900,00
|
41
|
900,00
|
41000,00
|
1167,36
|
|
4
|
момент
погашения 10.10.08
|
26.03.08
|
38
|
1400,00
|
79
|
2300,00
|
41000,00
|
2249,31
|
|
5
|
|
19.04.08
|
23
|
500,00
|
23
|
500,00
|
40949,31
|
654,05
|
|
6
|
|
25.05.08
|
36
|
830,00
|
59
|
1330,00
|
40949,31
|
1677,78
|
|
7
|
|
05.06.08
|
10
|
1100,00
|
69
|
2430,00
|
40949,31
|
1962,15
|
|
8
|
|
28.07.08
|
53
|
1500,00
|
53
|
1500,00
|
40481,46
|
1489,94
|
|
9
|
|
15.08.08
|
17
|
170,00
|
17
|
170,00
|
40471,40
|
477,79
|
|
10
|
|
11.09.08
|
26
|
900,00
|
43
|
1070,00
|
40471,40
|
1208,52
|
|
11
|
|
10.10.08
|
29
|
|
72
|
1070,00
|
40471,40
|
2023,57
|
2. Алгоритм решения:
Столбцы А «Исходные данные долг + %»,
В
«Момент открытия кредита. Дни поступления платежей и дата погашения»,
D «Величина платежа» заполняются исходя из первоначальных
данных постановки задачи.
Столбец С «Количество дней между поступлением
платежей» рассчитывается с использованием: «Вставка» - «Функция» - «Дата и
время» - «Дней360».
Столбец Е «Кол-во дней от последнего списания
долга» рассчитывается по формуле: = ЕСЛИ(F3<H3;E3+C4;C4). Используем «Вставка»
- «Функция» - «Логические» - «Если».
Пояснение:
если платеж меньше начисленных процентов, то проценты не погашаются, платежи
суммируются и соответственно складываются дни, если нет списания долга. Данное
условие дано для всего периода погашения долга.
Столбец F
«Накопленные платежи»: =ЕСЛИ(F3<H3;F3+D4;D4).
Пояснение: суммируются платежи, если
они меньше %. Данное условие дано для всего периода погашения долга.
Столбец G
«Остаток долга после
поступления платежа»: =ЕСЛИ(F3<H3;G3;G3+H3-F3).
Пояснение: если платежи были меньше начисленных процентов, то долг не
погашается, а переносится на следующий период. А если платежи больше начисленных
процентов, то к основному долгу прибавляются проценты и вычитается платеж.
Данное условие дано для всего периода погашения долга.
Столбец Н «Процент»: =G3*0,18*E3/360.
Пояснение: вычисление
начисленных процентов проводится с учетом количества дней от последнего
списания долга.
3. Ответ: Клиент должен вернуть 10.10.2008г. сумму
в размере 42494,97 руб.
4. Список литературы
1. «Информационные
системы в экономике» - Методические указания по выполнению контрольной работы.
– Москва: Вузовский учебник, 2007г.
2. «Информационные
системы в экономике» - Учебное пособие под редакцией профессора А.Н.Романова,
профессора Б.Е. Одинцова – Москва: Вузовский учебник, 2008г.