Контрольные задания

Задание 1.


Приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).

Требуется:

1) Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания:

B1=0,3; B2 =0,6; B3 = 0,3.

2) Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.

3) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

4) Отразить на графике фактические, расчетные и прогнозные данные.


Исходные данные:

 Квартал

Кредиты

1

35

2

44

3

52

4

34

5

37

6

48

7

59

8

36

9

41

10

52

11

62

12

38

13

46

14

56

15

67

16

41

Решение:

 I.                   Постройка модели.

t=1,2,…,n

Расчеты производятся последовательно:

Yr(t)= [a(t-1)+b(t-1)]*F(t-l)

a(t)= B1*Y(t)/F(t-l)+(1-B1)*[a(t-1)+b(t-1)]

b(t)= B3[a(t)-a(t-1)]+(1-B3)*b(t-1)

F(t)= B2*Y(t)/a(t)+(1-B2)*F(t-l)

Находим a и b: с помощью программы «мастер диаграмм» построим график с линией тренда и уравнением

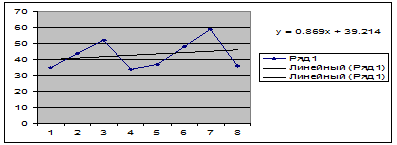
Из данного уравнения y = 0.869x + 39.214 мы берем a=39.214 и b=0.869

1) По формуле y(t)=a+t*b найдем y(t)

y(1)= 39.2+1*0.87=40.08;

y(2)= 39.2+2*0.87=40.95;

y(3)= 39.2+3*0.87=41.82


y(t)

t

Y(t)

Yr(t)

a(t)

b(t)

F(t)

e(t)

e(t)^2

I=e(t)/Y(t)

 

-3

 

 

 

 

0.86

 

 

 

 

-2

 

 

 

 

1.08

 

 

 

 

-1

 

 

 

 

1.27

 

 

 

 

0

 

 

39.21

0.87

0.79

 

 

 

40.08

1

35

34.52

40.25

0.92

0.87

0.48

0.23

0.01

40.95

2

44

44.35

41.07

0.89

1.07

-0.35

0.13

0.01

41.82

3

52

53.41

41.63

0.79

1.26

-1.41

1.99

0.03

42.69

4

34

33.43

42.63

0.85

0.79

0.57

0.33

0.02

43.56

5

37

37.67

43.25

0.78

0.86

-0.67

0.45

0.02

44.43

6

48

47.29

44.24

0.84

1.08

0.71

0.51

0.01

45.30

7

59

56.75

45.62

1.01

1.28

2.25

5.08

0.04

46.17

8

36

37.01

46.24

0.89

0.78

-1.01

1.02

0.03

 

9

41

40.52

47.30

0.94

0.86

0.48

0.23

0.01

 

10

52

52.13

48.21

0.93

1.08

-0.13

0.02

0.00

 

11

62

62.87

48.93

0.87

1.27

-0.87

0.76

0.01

 

12

38

39.07

49.39

0.75

0.78

-1.07

1.15

0.03

 

13

46

43.32

51.07

1.03

0.89

2.68

7.20

0.06

 

14

56

56.23

52.03

1.01

1.08

-0.23

0.05

0.00

 

15

67

67.46

52.93

0.97

1.27

-0.46

0.21

0.01

k

16

41

41.80

53.59

0.88

0.77

-0.80

0.64

0.02

1

17

 

48.26

 

 

 

 

 

 

2

18

 

59.65

 

 

 

 

 

 

3

19

 

71.32

 

 

 

 

 

 

4

20

43.93

 

 

 

 

 

 

 

 

748

 

 

 

 

SS=

19.97

0.31

а=

39.21

В1=

0.3



Eотн=

1.9373

b=

0.87

В2=

0.6





В3=

0.3





2) F(-3)= (Y(1)/y(1)+Y(5)/y(5)/2=(35/40.08+37/43.46)/2=0.86;

F(-2)= (Y(2)/y(2)+Y(6)/y(6)/2=(44/40.95+48/44.43)/2=1.08;

F(-1)= (Y(3)/y(3)+Y(7)/y(7)/2=(52/41.82+59/45.30)/2=1.27;

F(0)= (Y(4)/y(4)+Y(8)/y(8)/2=(34/42.69+36/46.17)/2=0.79;

3) По формуле a(t)=B1*Y(t)/F(t-l)+(1-B1)*[a(t-1)+b(t-1)] найдем a(t)

a(1)= 0.3*35/0.86+(1-0.3)*(39.21+0.87)=40.25

4) По формуле b(t)=B3[a(t)-a(t-1)]+(1-B3)*b(t-1) найдем b(t)

b(1)= 0.3*(39.21-40.25)+(1-0.3)*0.87=0.92

a(2)= 0.3*44/1.08+(1-0.3)*(40.25+0.92)=41.07

b(2)= 0.3*(40.25-41.07)+(1-0.3)*0.92=0.89

5) По формуле F(t)=B2*Y(t)/a(t)+(1-B2)*F(t-1) найдем F(t)

F(1)= 0.6*35/40.25+(1-0.6)*0.86=0.87

a(5)= 0.3*37/0.87+(1-0.3)*(42.63+0.85)=43.25

b(5)= 0.3*(43.25-42.63)+(1-0.3)*0.85=0.78

6) По формуле Yr(t)=[a(t-1)+b(t-1)]*F(t-l) найдем Yr(t)

Yr(1)= (39.21+0.87)*0.86=34.52

Yr(2)= (40.25+0.92)*1.08=44.35

Yr(3)= (41.07+0.89)*1.27=53.41

7)  По формуле e(t)=Y(t)-Yr(t) найдем e(t)

e(1)=35-34.52=0.48

e(2)= 44-44.35=-0.35

e(3)= 52-53.41=-1.41

8) e(t)^2=e(t)*e(t)

e(1)^2= 0.48*0.48=0.23

e(2)^2= (-0.35)*(-0.35)=0.13

e(3)^2= (-1.41)*(-1.41)=1.99

Итоговая сумму e(3)^2=SS=19.97

9) По формуле I=e(t)/Y(t) найдем I

I 1= 0.48/35=0.01

I 2= (-0.35)/44=0.01

I 3= (-1.41)/52=0.03

Итоговая сумма I=0.31

II.                  Оценка точности.

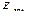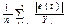 =  ∙ 100%


E отн. =0.31/16*100=1.937278

III.                  Прогноз на год вперед.

Шаг прогноза.

Время,

Значение y ∙ (t + k)

1

17

48.26

2

18

59.65

3

19

71.32

4

20

43.93

y ∙ (t + k) = 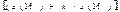 ∙ F(t+k-4)


y(17) = (53.59 +1 ∙ 0.88) ∙ 0.89 = 54.47 ∙ 0.89 = 48.26

y(18) = (53.59 +2 ∙ 0.88) ∙ 1.08 =  55.35 ∙ 1.08 = 59.65

y(19) = (53.59 +3 ∙ 0.88) ∙ 1.27 = 56.23 ∙ 1.27 = 71.32

y(20) = (53.59 +4 ∙ 0.88) ∙ 0.77 = 57.11 ∙ 0.77 = 43.93       

Видна сезонность за эти 4 года

IV.                  Построение графика.

График строим по данным таблицы.

T

Y(t)

Yr(t)

1

35

34.52

2

44

44.35

3

52

53.41

4

34

33.43

5

37

37.67

6

48

47.29

7

59

56.75

8

36

37.0

9

41

40.52

10

52

52.13

11

62

62.87

12

38

39.07

13

46

43.32

14

56

56.23

15

67

67.46

16

41

41.08

17

 

48.26

18

 

59.65

19

 

71.32

20

 

43.93

На нижеприведённом рисунке проводится сопоставление фактических и расчётных данных. Здесь же показаны прогнозные значения цены акции на 1 год вперёд. Из рисунка видно, что расчётные данные хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

Задание 2.

Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням. Рассчитать:

- экспоненциальную скользящую среднюю;

- момент;

- скорость изменения цен;

- индекс относительной силы;

- %R,%К и % D.

Расчёты проводить для всех дней, для которых эти расчёты можно выполнить на основании имеющихся данных.

t

Цены

макс.

мин.

Ct

1

718

660

675

2

685

601

646

3

629

570

575

4

585

501

570

5

598

515

523

6

535

501

506

7

555

500

553

8

580

540

570

9

580

545

564

10

603

550

603






Решение:

Для вычисления экспоненциальной средней найдем коэффициент k

Дни

Ct

1

675

2

646

3

575

4

570

5

523

6

506

7

553

8

570

9

564

10

603

n=5

k =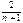

k =  =  =

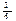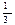
Находим значение EMA по формуле

EMAt = k ∙ Ct + (1 – k) ∙ EMAt – 1

Находим EMAo=C1+C2+C3+C4+C5/5= 675+646+575+570+523/5=597.80

EMA(1)= 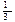 ∙ 675 + (1-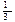)∙ 597.80 = 623.28

EMA(2)= 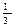 ∙ 646 + (1-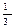)∙ 623.28 = 630.77

EMA(3)= 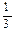 ∙ 575 + (1-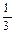)∙ 630.77 = 612.37

Дни

Ct

EMA

1

675

623.28

2

646

630.77

3

575

612.37

4

570

598.39

5

523

573.51

6

506

551.23

7

553

551.82

8

570

557.82

9

564

559.86

10

603

574.09

1) Ct-Ct-1

 Ct-Ct-1=C(2)-C(2-1)=646-675= -29

C(3)-C(3-1)=575-646= -71

C(4)-C(4-1)=570-575= -5

C(5)-C(5-1)=523-570= -47

C(6)-C(6-1)=506-523= -17

C(7)-C(7-1)=553-506= 47

C(8)-C(8-1)=570-553= 17

C(9)-C(9-1)=564-570= -6

C(10)-C(10-1)=603-564= 39

2) Найдем прирост конечных цен за 5 последних дней (AU):

AU(7)=47

AU(8)=47+17=67

AU(9)=47+17=67

AU(10)=47+17+39=103

3) Найдем убыль конечных цен за 5 последних дней (AD):

AD(6)= (-29)+(-71)+(-5)+(-47)+ (-17)= -169=169

AD(7)= (-71)+(-5)+(-47)+ (-17)= -140=140

AD(8)= (-5)+(-47)+ (-17)= -69=69

AD(9)= (-47)+ (-17)+ (-6)= -70=70

AD(10)= (-17)+ (-6)= -23=23

4) Сумма прироста и убытка цен за 5 последних дней (AU+AD):

AU(6)+AD(6)= 0+169=169

AU(7)+AD(7)= 47+147=187

AU(8)+AD(8)= 64+69=133

AU(9)+AD(9)= 64+70=134

AU(10)+AD(10)= 103+23=126

5) Найдем индекс относительной силы за 5 последних дней (RSI):

RSI=AU/(AU+AD)*100%

RSI(6)=0

RSI(7)=47/187*100=25.13

RSI(8)=64/133*100=48.12

RSI(9)=64/134*100=47.76

RSI(10)=103/126*100=81.75

6) Найдем момент за 5 последних дней (MOM):

MOM=C6-C1

MOM(6)=506-675=-169=169

MOM(7)=553-646=-93=93

MOM(8)=570-575=-5=5

MOM(9)=564-570=-6=6

MOM(10)=603-523=80

7) Найдем скорость изменения цен за 5 последних дней (ROC):

ROC=C6/C1*100%

ROC(6)=506/675*100%=74.96

ROC(7)=553/646*100%=85.60

ROC(8)=570/575*100%=99.13

ROC(9)=564/570*100%=98.95

ROC(10)=603/523*100%=115.30

8) Найдем min и max значения цены за 5 дней (H5-L5)

H5-L5(5)=718-501=217

H5-L5(6)=685-501=184

H5-L5(7)=629-500=129

H5-L5(8)=598-500=98

H5-L5(9)=598-500=98

H5-L5(10)=603-500=103

9) Ct-L5

Ct-L5(5)=523-501=22

Ct-L5(6)=506-501=5

Ct-L5(7)=553-500=53

Ct-L5(8)=570-500=70

Ct-L5(9)=564-500=64

Ct-L5(10)=603-500=103

10) Найдем цену индекса за 5 дней (%Kt)

%Kt=(Ct-L5)/(H5-L5)*100%

%Kt(5)=22/184*100=10.14

%Kt(6)=5/184*100=2.72

%Kt(7)=53/129*100=41.09

%Kt(8)=70/98*100=71.43

%Kt(9)=64/98*100=65.31

%Kt(10)=103/103*100=100

11) %Rt

%Rt=100-%Kt

%Rt(5)=100-10.14=89.86

%Rt(6)=100-2.72=97.28

%Rt(7)=100-41.09=58.91

%Rt(8)=100-71.43=28.57

%Rt(9)=100-65.31=34.69

%Rt(10)=100-100=0

12) Σ(Ct-C5)

Σ(Ct-C5)(7)=10.14+2.72+41.09=53.94

 Σ(Ct-C5)(8)=2.72+41.09+71.43=115.23

Σ(Ct-C5)(9)=41.09+71.43+65.31 =177.82

Σ(Ct-C5)(10)=71.43+65.31+100 =236.73

13) Σ(H5-L5)

Σ(H5-L5)(7)=217+184+129=530

Σ(H5-L5)(8)=184+129+98=411

Σ(H5-L5)(9)=129+98+98=325

Σ(H5-L5)(10)=98+98+103=299

14) %Dt

%D= Σ(Ct-C5)/ Σ(H5-L5)*100%

%D(7)=53.94/530*100=10.18

%D(8)=115.23/411*100=28.04

%D(9)=177.82/325*100=54.71

%D(10)=236.73/103*100=79.18

Задание 3.

Выполнить различные коммерческие расчеты, используя данные, приведенные в таблице. В условии задачи значения параметров приведены виде переменных. Например, S означает некую сумму средств в рублях, T лет – время в годах, i – ставку в процентах и т.д. По именам переменных из таблицы необходимо выбрать соответствующие численные значения параметров и выполнить расчет.


Сумма

Дата началтная

Дата конечная

Время в днях

Время в годах

Ставка

Число начислений

S

Tн

Tк

Tдн

Tлет

i

m

2 500 000

15.01.2002

15.03.2002

180

4

30

2

3.1. Банк выдал ссуду, размером 2 500 000 руб. Дата выдачи ссуды – 15.01.2002, возврата – 15.03.2002. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке 0.3 % годовых.

Найти:

3.1.1) точные проценты с точным числом дней ссуды;

3.1.2) обыкновенные проценты с точным числом дней ссуды;

3.1.3) обыкновенные проценты с приближённым числом дней ссуды.

Решение:

Дано:

 

S = 2 500 000 руб.             - сумма


Tн = 15.01.02                   - начальная дата


Tк = 15.03.02                   - конечная дата


i= 30% = 0,3%                - процентная ставка

———————————————                             

Рассчитываем по формуле I= S* i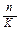

а) K = 365, n = 59

 

  n = 17 + 28 + 14 = 59

 

  I=2 500 000 * 0.3 = 2 500 000 * 0,048 = 120 000 руб.;

б) K = 360, n = 59

   I=2 500 000 * 0.3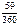 = 2 500 000 * 0.049 = 122 500 руб.;

в) K = 360, n = 57

 

   I=2 500 000 * 0.3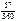 = 2 500 000 * 0.047 = 117 500 руб..

 

Ответ:


Точные проценты с точным числом дней ссуды составляют 120 000 руб.,

обыкновенные проценты с точным числом дней ссуды составляют 122 500руб., обыкновенные проценты с приближённым числом дней ссуды составляют 117 500 руб.

Задание 3.2.


Через 180 дней после подписания договора должник уплатит 2 500 000 руб. Кредит выдан под 0.3 % годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

Решение:

Дано:

 

S = 2 500 000 руб.

 

Тдн = 180


i = 0.3%

 

Найти:

 

P, D - ?

———————————————

Рассчитываем по формулам   P = S / (1  + i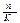),  D = S – P

 

P = 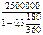 =  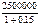=  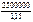= 2 173 913 руб.


D = 2 500 000 – 2 173 913 = 326 087 руб.

Ответ:

 

Первоначальная сумма составляет 2 173 913 руб., дисконт равен 326 087 руб.

Задание 3.3.

Через 180 дней предприятие должно получить по векселю 2 500 000 руб. Банк приобрёл этот вексель с дисконтом. Банк учёл вексель по учётной ставке 0.3% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

Решение:

Дано:

 

S = 2 500 000 руб.


Тдн = 180


i = 0.3%


Найти:

 

P, D - ?

———————————————

Рассчитываем по формулам   D = S ∙ i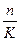,  P = S – D

D = 2 500 000 * 0.3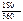 = 2 500 000 * 0.15 = 375 000 руб.

P = 2 500 000 – 375 000 = 2 125 000 руб.

Ответ:

Полученная предприятием сумма составляет 2 125 000 руб., дисконт равен 375 000 руб.

Задание 3.4.

В кредитном договоре на сумму 2 500 000 руб. и сроком на 4 года, зафиксирована ставка сложных процентов, равная 0,3 % годовых. Определить наращенную сумму.


Решение:

Дано:

 

S = 2 500 000 руб.


Тлет = 4 года

 

i = 0.3%

Найти:


Наращенная сумма - ?

———————————————

Рассчитываем по формуле  P=S ∙ (1 + i)Тлет

 

P=2 500 000 * (1 + 0.3)4  = 2 500 000 * 1.34  = 2 500 000 * 2.8561 = 7 140 250 руб.

 

Ответ:

 

Наращенная сумма составляет 7 140 250 руб.

Задание 3.5.

Ссуда, размером 2 500 000  руб. предоставлена на 4 лет. Проценты сложные, ставка – 0.3% годовых. Проценты начисляются 2 раза в году. Вычислить наращенную сумму.


Решение:

Дано:

 

S = 2 500 000 руб.

 

Тлет = 4 года

 

i = 0.3%

 

m = 2                  - число начислений процентов в году

 

Найти:

 

Наращенная сумма - ?

———————————————

Рассчитываем по формуле  P=S ∙ (1 + 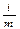)Tлет ∙m

 

P=2 500 000 * (1 + )4 ∙ 2 = 2 500 000 * 1.58 = 2 500 000 * 3,059 = 7 647 500 руб.

Ответ:


Наращенная сумма составляет 7 647 500 руб.

Задание 3.6.

Вычислить эффективную ставку процента, если банк начисляет проценты 2 раза в году, исходя из номинальной ставки 0.3 % годовых.

 

Решение:                                                                                                                        


Дано:


m = 2


i = 0.3%


Найти:

 

iэф - ?

———————————————

Рассчитываем по формуле  iэф = (1 + 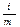)m – 1


iэф = (1 + 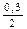)2 – 1 = 1.152 – 1 = 1.3225 – 1 = 0.3225 = 32.25%


Ответ:


Эффективная ставка процента составляет 32.25%.

Задание 3.7.

Определить, какой должна быть номинальная ставка при начислении процентов 2 раза в году, чтобы обеспечить эффективную ставку 0.3% годовых.


Решение:

Дано:

m = 2

i = 0.3%

Найти:

 

iном - ?

———————————————

Рассчитываем по формуле   iном =m* [(1 + iэф) 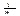 - 1]

iном = 2*[(1 + 0,3)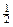 - 1] = 2*( 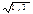- 1)= 2*(1,14017 – 1)= 2*0.14017=


= 0.28034 = 28.03%

 

Ответ:

Номинальная ставка составляет 28,03%

Задание 3.8.

Через 4 года предприятию будет выплачена сумма 2 500 000. Определить её современную стоимость при условии, что применяется сложная процентная ставка 0.3 % годовых.


Решение:

 

Дано:

 

S = 2 500 000 руб.

 

Тлет = 4 года

 

i = 0.3%

 

Найти:

 

P - ?

———————————————

Рассчитываем по формуле   P =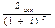

 

P = 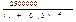 =  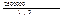=  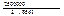= 875 319.49 руб.


Ответ:

 

Современная стоимость составляет 875 319.49 руб.

Задание 3.9.

Через 4 года по векселю должна быть выплачена сумма 2 500 000 руб. Банк учёл вексель по сложной учётной ставке 0.3 % годовых. Определить дисконт.


Решение:

 

Дано:

 

S = 2 500 000 руб.

 

Тлет = 4 года

 

i = 0.3%

 

Найти:

 

D - ?

———————————————

Рассчитываем по формулам   P = Sисх ∙ (1 – i)Тлет,  D = S – P

 

P = 2 500 000 * (1 – 0.3)4 = 2 500 000 * 0.74 = 0.2401 * 2 500 000 = 600 250 руб.


D = 2 500 000 – 600 250 = 1 899 750 руб.


Ответ:


Дисконт составляет 1 899 750 руб.

Задание 3.10.


В течение 4 лет на расчётный счёт в конце каждого года поступает по 2 500 000 руб., на которые m раз в году начисляются проценты по сложной годовой ставке 0.3 %. Определить сумму на расчётном счёте к концу указанного срока.

Решение:

 

Дано:

 

S = 2 500 000 руб.

 

Тлет = 4 года

 

i = 0.3%

 

m = 2   


Найти:


Сумма на расчётном счёте - ?

———————————————

Рассчитываем по формуле


Р = S * ((1 + i эф)n – 1)/ i эф

Р = S * ((1 + i эф)n – 1)/ i эф= 2 500 000 * (1 + 0.32)4– 1)/ 0.32= 15 905 920 руб.

Ответ:

 

Сумма на расчётном счёте составляет 15 905 920 руб.