ВВЕДЕНИЕ

В последнее время специалисты, обладающие знаниями и навыками проведения прикладного экономического анализа с использованием доступных математических и программных средств, пользуются спросом на рынке труда. Одной из центральных дисциплин в подготовке таких специалистов является дисциплина "Эконометрика".

Эконометрика является областью знаний, которая охватывает вопросы применения статистических методов к теоретическим моделям, описывающим реальные экономические процессы.

Очевидно, что с помощью моделей можно получить много информации об экономических процессах, объяснить те или иные явления или процессы, но никогда не удастся получить всю информацию и однозначно определить истинный механизм экономического процесса или явления.

И даже в тех случаях, когда достаточно адекватная исходным данным эконометрическая модель построена и вопрос только в использовании ее для объяснения экономической ситуации или принятия решения, следует весьма осторожно подходить к выводам и рекомендациям, следующим из модельных оценок.

Эконометрический анализ, как правило, проводят с помощью ПЭВМ. В последние несколько лет сформировался обширный набор из пакетов прикладных программ, позволяющих автоматизировать процессы такого анализа. К наиболее распространенным относятся пакеты SAS, SPSS, Stata и другие. Имеются простейшие опции для проведения эконометрического анализа в Ехсе1.

Но для специфических и конкретных применений эконометрических методов использование этих универсальных пакетов избыточно и достаточно использования специально разработанных программных продуктов под конкретную задачу.

Целью настоящей дипломной работы является создание программного продукта построения модели авторегрессии по методу Койка и исследование ее параметров. При этом программа должна предъявлять низкие требования к аппаратному обеспечению компьютера, быть доступна в использовании непрофессиональному пользователю, предоставлять удобный и интуитивно понятный интерфейс к функциям программы.

1 МОДЕЛИ ВРЕМЕННЫХ РЯДОВ

1.1 Классическая мультипликативная модель

Временным рядом называют серию числовых величин, полученных через регулярные промежутки времени. Например временными рядами будут серия ежедневных наблюдений в течение некоторого периода за ценами товара при закрытии торгов на бирже, дневные объемы выпуска товара, месячные показатели инфляции или индекса потребительских цен, ежеквартальные оценки валового национального продукта (принятые в США) или средних зарплат (принятые в России для ежеквартального индексирования пенсий), ежегодные данные об объеме, выручке и прибыли компании. Временные ряды, естественно, не ограничиваются исключительно экономическими величинами; известно их использование при анализе процессов в энергосистемах, атомной промышленности, химических и нефтехимических производствах, причем в этом случае часто используются более мелкие дискретности времени, чем в экономике - минуты и даже секунды при обработке данных о быстропротекающих процессах в атомной энергетике или при исследовании переходных процессов в химической кинетике. Известно даже успешное применение анализа временных рядов при слежении за подводными лодками "вероятного противника" в 70-80-е годы, и при обработке данных наблюдений в системах ПВО, и при прогнозах проходимости радиосигналов в атмосфере и ионосфере, и при моделировании транспортных потоков на автотрассах.

Основным положением, на котором базируется использование временных рядов для прогнозирования, является то, что факторы, влияющие на отклик изучаемой системы, действовали некоторым образом в прошлом и настоящем, и ожидается, что они будут действовать схожим образом и в не слишком далеком будущем. Поэтому основной целью анализа временных рядов будет оценка и вычленение этих влияющих факторов с целью прогноза дальнейшего поведения системы и выработки рациональных управленческих решений.

В свое время были разработаны многие методы вычленения влияющих факторов и оценки их взаимодействия и влияния на отклик системы, но пожалуй наиболее фундаментальной является классическая мультипликативная модель временного ряда, широко используемая при анализе ежемесячных, ежеквартальных и ежегодных данных, и потому чаще всего используемая в экономических исследованиях.

Характеризуя полученные данные можно выделить общую тенденцию (движения на повышение или понижение), которую принято называть трендом.

Тренд, однако, не является единственной составляющей ряда. На фоне отчетливого повышения отклика можно выделить периоды ускоренного и замедленного роста, а иногда и падения объема продаж. Считается, что тренд осложнен существованием циклической компоненты (циклической составляющей) и нерегулярной компоненты. При анализе рядов с более коротким шагом (квартальные или месячные данные) обнаруживаются и короткопериодичные отклонения от тренда, повторяющиеся с той или иной устойчивостью из года в год; эти отклонения объясняют существованием сезонной компоненты в отклике.

Циклическая компонента объясняет отклонения от тренда с периодичностью от 2 до 10 лет; обычно эта компонента может изменяться по длине периода и своей интенсивности и хорошо коррелирует с циклом деловой активности. На подъеме деловой активности значения отклика оказываются выше чисто трендовых, а в периоды спада и стагнации оказываются заметно ниже ожидаемых по тренду.

Сезонная компонента определяет короткопериодические колебания, связанные именно с изменениями внутригодовой активности, и повторяющиеся через более или менее фиксированные моменты времени; отслежены они, естественно, могут быть при ежеквартальных, ежемесячных и более частых наблюдениях. Естественно связать сезонную компоненту с влиянием традиций (сезонные и рождественские распродажи), социальных привычек (высокая активность в курортном бизнесе в летнее время и существование "мертвых сезонов" в иные периоды), религиозных факторов (рождественские и пасхальные поездки к родственникам или друзьям в христианских странах, продажи пищевых продуктов и общественное питание во время мусульманского поста) и даже плохо предсказуемой погоды (продажи мороженого и прохладительных напитков, деятельность горнолыжных курортов).

Нерегулярная компонента вызывает отклонения от хода отклика, определяемого трендовой, циклической и сезонной составляющими. Она может быть рассмотрена как случайная, и потому непрогнозируемая; в терминах статистики ее можно считать ошибкой наблюдения и обрабатывать аналогично случайным ошибкам измерений в статистике. Связывают ее обычно со случайными явлениями внешнего мира - ураганами, наводнениями, забастовками, влиянием политических процессов, таких как выборы или неопределенность их исхода, переворотами и мятежами.

1.2 Компоненты классической модели – сравнение

В классической мультипликативной модели временных рядов постулируется, что наблюдаемое значение отклика в любой точке временного ряда является произведением трех факторов - тренда, циклической и нерегулярной компоненты (в случае короткошаговых наблюдений - четырех, добавляется еще сезонная компонента), и любое значение ряда может быть представлено в виде

Yi = Ti * Ci * Si * Ii,

где Yi - значение отклика, а Ti, Ci, Si, Ii - соответственно значения трендовой, циклической, сезонной и нерегулярной компонент в любой точке ряда. В таблице приведено сравнение компонент классической модели.

Факторы, влияющие на значения временного ряда

Компонента

Классификация

Определение

Причины воздействия

Продолжитель-ность

Тренд

Систематическая

Общая устойчивая долговременная тенденция

Изменения в технологии, численности населения, благосостоянии, системе ценностей

Несколько лет

Циклическая

Систематическая

Повторяющиеся подъемы и спады, проходящие 4 фазы: пик, рецессия, депрессия, подъем

Взаимодействие множественных комбинаций факторов, влияющих на экономику

Обычно 2-10 лет с изменяющейся интенсивностью

Сезонная

Систематическая

Достаточно регулярные периодические флуктуации, происходящие в каждом 12-месячном периоде из года в год

Погодные условия, социальные привычки, религиозные традиции

В течение ~12 месяцев (квартальные и месячные наблюдения)

Нерегулярная

Случайная

Остаточная флуктуация, рассматривающаяся как "связанная с ошибкой" и остающаяся после того, как учтены систематические эффекты

Случайные вариации в данных, вызванные непредвиденными событиями

Обычно короткой продолжительности и не повторяющиеся

При анализе данных методом временных рядов вначале обычно строят график зависимости отклика по времени для определения общей долговременной тенденции, повышающего или понижающего тренда. Если данные сильно осциллируют и общий тренд не угадывается, может потребоваться сглаживание временного ряда, после выполнения которого тренд обычно выявляется. В дальнейшем для описания временного ряда используется один из методов регрессии данных ряда на временную ось и полученное регрессионное описание используется в целях прогнозирования.


1.3 Виды временных рядов

Совокупность наблюдений у(t1),у(t2).. анализируемой величины У(t), произведенных в последовательные моменты времени ti называется временным рядом.

Иначе говоря, временной ряд - это упорядоченная во времени последовательность наблюдений.

Среди временных рядов выделяют одномерные. полученные в результате наблюдения одной, фиксированной характеристики исследуемого объекта, и, многомерные временные ряды как результат наблюдений нескольких характеристик одного исследуемого объекта в течение ряда моментов времени.

По времени наблюдения временные ряды делятся на дискретные и непрерывные. Дискретные ряды, в свою очередь, разделяются на ряды с равноотстоящими и произвольными моментами наблюдения.

Временные ряды бывают детерминированными и случайными: первые получены как значения некоторой неслучайной функции, а вторые - как реализации случайной величины.

Стохастические временные ряды подразделяются на стационарные и нестационарные. Ряд у(t) называется стационарным (в узком смысле), если среднее, дисперсия и ковариации у(t) не зависят от t.

В дальнейшем, если не оговорено иначе, будем рассматривать одномерные, дискретные с равноотстоящими моментами наблюдений случайные временные ряды.

Природа временных рядов существенно отличается от природы пространственных данных, что проявляется в весьма специфических свойствах временных рядов. В своей работе исследователь должен учитывать эти особенности, основные из которых отображены в таблице 1.1.



Таблица 1.1

Особенности временных рядов


Характеристики наблюдений

Тип данных

Пространственные данные

Временные ряды

Порядок

Не существенен

Существенен

Статистическая независимость

Независимы

Не являются статистически независимыми

Функция распределения

Распределены одинаково

Распределены неодинаково

Количество

Как правило, большое

Как правило, небольшое

Значения элементов временного ряда формируются под воздействием ря -да факторов, среди которых выделяют:

•     долговременные,  формирующие  в длительной перспективе общую тенденцию анализируемого признака. Эта тенденция описывается с помощью некоторой функции, называемой трендом (Т);

•     сезонные, формирующие периодически повторяемые в определенное время года колебания анализируемого признака (S);

•     циклические, формирующие изменения анализируемого в результате воздействия циклов экономической, демографической или астрофизической природы (С);

•     случайные, не поддающиеся учету и регистрации, как результат воз действия случайных, внешних факторов (U).

Первые три составляющие часто объединяют в одну детерминированную и рассматривают модель ряда в виде yt=f(t)+Ut, Vt. Изменение уровня f(t) со временем называют при этом трендом.

Предметом анализа временного ряда является выделение и изучение указанных компонент ряда, как правило в рамках одной из моделей ряда, либо аддитивной Y=T+C+S+U, либо мультипликативной Y=T -С -S • U

Некоторые составляющие могут отсутствовать в тех или иных рядах.

В результате анализа временного ряда необходимо определить, какие из неслучайных составляющих присутствуют в разложении ряда, построить для них хорошие оценки, подобрать модель, описывающую поведение остатков и оценить ее параметры.

2 АНАЛИЗ МОДЕЛИ РАСПРЕДЕЛЕННЫХ ЛАГОВ   

2.1 ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ И МОДЕЛЕЙ АВТОРЕГРЕССИИ


 В эконометрике к числу динамических относятся не все модели, построенные по временным рядам данных. Термин «динамический» в данном случае характеризует каждый момент времени t в отдельности, а не весь период, для которого строится модель. Эконометрическая модель является динамической, если в данный момент времени  она учитывает значения входящих в нее переменных, относящиеся как к текущему, так и к: предыдущим моментам времени, т. е. если эта модель отражает динамику исследуемых переменных в каждый момент времени.

Можно выделить два основных типа динамических эконометрических моделей. К моделям первого типа относятся модели aвторегрессии и модели с распределенным лагом, в которых значения переменной за прошлые периоды времени (лаговые переменные) непосредственно включены в модель. Модели второго типа учитывают динамическую информацию в неявном виде. В эти модели включены переменные, характеризующие ожидаемый или желаемый уровень результата, или одного из факторов в момент времени t. Этот уровень считается неизвестным и определяется экономическими единицами с учетом информации, которой они располагают в момент .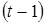

В зависимости от способа определения ожидаемых значений показателей различают модели неполной корректировки, адаптивных ожиданий и рациональных ожиданий. Оценка параметров этих моделей сводится к оценке параметров моделей авторегрессии.

При исследовании экономических процессов нередко приходится моделировать ситуации, когда значение результативного признака в текущий момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени 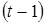, , ..., . 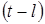Например, на выручку от реализации или прибыль компании текущего периода могут оказывать влияние расходы на рекламу или поведение маркетинговых исследований сделанные компанией в предшествующие моменты времени. Величину l, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, – лаговыми переменными.

Разработка экономической политики как на макро-, так и на микроуровне требует решения обратного типа задач, т. е. задач, определяющих, какое воздействие окажут значения управляемых переменных текущего периода на будущие значения экономических показателей. Например, как повлияют инвестиции в промышленность на валовую добавленную стоимость этой отрасли экономики будущих периодов или как может измениться объем ВВП, произведенного в периоде (t + 1), под воздействием увеличения денежной массы в периоде t?

Эконометрическое моделирование охарактеризованных выше процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели называются моделями с распределенным лагом. Модель вида

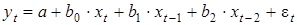
является примером модели с распределенным лагом.

Наряду с лаговыми значениями независимых, или факторных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Например, потребление в момент времени t формируется под воздействием дохода текущего и предыдущего периодов, а также объема потребления прошлых периодов, например, потребления в период 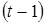 . Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Модель вида

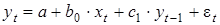
Относится к моделям авторегрессий.

Построение моделей с распределенным лагом и моделей авторегрессии имеет свою специфику. Во-первых, оценка параметров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК ввиду нарушения его предпосылок и требует специальных статистических методов. Во-вторых, исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры. Наконец, в-третьих, между моделями с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.


2.2 ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ


Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна:

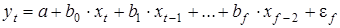
Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение l следующих моментов времени.

Коэффициент регрессии 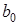  при переменной  характеризует среднее абсолютное изменение у, при изменении х на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.

В момент (t + 1) совокупное воздействие факторной переменной х, на результату, составит 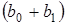 усл. ед., в момент (t+2) это воздействие можно охарактеризовать суммой 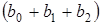 и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.

С учетом конечной величины лага можно сказать, что изменение переменной х, в момент t на 1 усл. ед. приведет к общему изменению результата через l моментов времени на  абсолютных единиц.

Введем следующее обозначение:

.

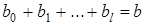Величину b называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде t + l результата у под влиянием изменения на 1 ед. фактора х.     

Предположим

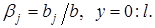
Назовем полученные величины относительными коэффициентами модели с распределенным лагом. Если все коэффициенты 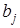имеют одинаковые знаки, то для любого  j.

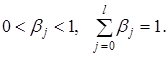
В этом случае относительные коэффициенты 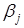 являются весами для соответствующих коэффициентов 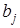 .  Каждый из них измеряет долю общего изменения результативного признака в момент времени (t +j).

Зная величины 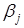, с помощью стандартных формул можно определить еще две важные характеристики модели множественной регрессии: величину среднего лага и медианного лага. Средний лаг определяется по формуле средней арифметической взвешенной:

.

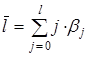и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени. Медианный лаг — это величина лага, для которого

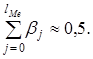
Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.


2.3 МЕТОД КОЙКА

Рассмотренные выше модели были построены в предположении конечной величины лага l. Предположим теперь, что для описания некоторого процесса используется модель с бесконечным лагом вида:

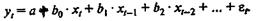
Очевидно, что параметры такой модели обычным МНК или с помощью иных стандартных статистических методов определить нельзя, поскольку модель включает бесконечное число факторных переменных. Однако, приняв определенные допущения относительно структуры лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т. е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической прогрессии.

Впервые изложенный в этом разделе подход к оценке параметров моделей с распределенным лагом типа был предложен Л.М. Койком. Койк предположил, что существует некоторый постоянный темп l. (0 <l< 1) уменьшения во времени лаговых  воздействий фактора на результат. Ёсли, например, в период t результат изменялся под воздействием изменения фактора в этот же период времени на b0 ед., то под воздействием изменения фактора, имевшего место в период (t — 1), результат изменится на b0 • l ед.; в период (t — 2) — на b0 • l•l ед., и т. д. Для некоторого периода (t — l) это изменение результата составит Ь0 •ll ед. В более общем виде можно записать:

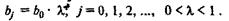
Ограничение на значения l>0 обеспечивает одинаковые знаки для всех коэффициентов bj > 0, а ограничение bj < 1 означает, что с увеличением лага значения параметров модели убывают в геометрической прогрессии. Чем ближе l к 0, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приводится на текущие значения фактора хt.

Выразим все коэффициенты bj в модели через b0 и l:

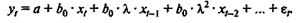
Тогда для периода (t — 1) модель можно записать следующим образом:

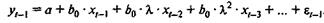
Умножим обе части модели на l:

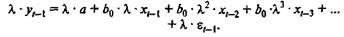
Вычтем найденное соотношение из предыдущего соотношения:  

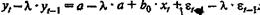
Преобразования приводят нас к получению модели Койка:

,

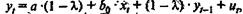где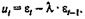


Полученная модель есть модель двухфакторной линейной регрессии (точнее — авторегрессии). Определив ее параметры, мы найдем l и оценки параметров а и b0 исходной модели. Далее несложно определить параметры b1, b2,.... Отметим, что применение обычного МНК к оценке параметров модели приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной yt-1.

Описанный выше алгоритм получил название преобразования Койка. Это преобразование позволяет перейти от модели с бесконечными распределенными лагами к модели авторегрессии, содержащей две независимые переменные xt и yt-1.

Несмотря на бесконечное число лаговых переменных в модели, геометрическая структура лага позволяет определить величины среднего и медианного лагов в модели Койка. Поскольку сумма коэффициентов регрессии в модели есть сумма геометрической прогрессии, т.е.:

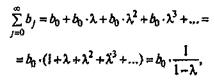
то средний лаг определяется как

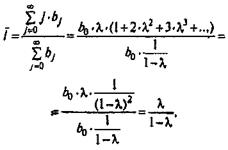
Нетрудно заметить, что при l = 0,5 средний лаг Т =1, а при l < 0,5 средний лаг T <1, т. е, воздействие фактора на результат в среднем занимает менее одного периода времени. Величину (1-l) интерпретируют обычно как скорость, с которой происходит адаптация результата во времени к изменению факторного признака. Для расчета медианного лага необходимо выполнение следующего условия:

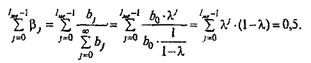
Поэтому медианный лаг в модели Койка равен:


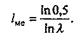
2.4 ОПИСАНИЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ


Как уже упоминалось в описании метода Койка для получения коэффициентов авторегрессии используется метод наименьших квадратов. Для описания этого метода рассмотрим обобщение линейной регрессионной модели для случая более двух переменных.

Пусть мы располагаем выборочными наблюдениями над k: переменными Yi, и Xji, j=1,..., k, i=1,2,.. ,n, где n - количество наблюдений.

Предположим, что существует линейное соотношение между результирующей переменной Y и k объясняющими переменными Х1, Х3, ...,Хk. Тогда с учетом случайной ошибки щ запишем уравнение:

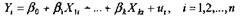
В данном уравнении  неизвестны коэффициенты Вj=0,2,...,k и параметры распределения ui. Задача состоит в оценивании этих неизвестных величин. Модель описываемая данным уравнением называется классической линейной моделью множественной регрессии (КЛММР). Заметим, что часто имеют в виду, что переменная Хо при В0 равна единице для всех наблюдений i=1,2,...,n.

Относительно переменных модели в приведенном уравнении примем следующие основные гипотезы:

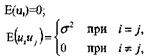
Х1,Х3,..., Xk - неслучайные переменные; Не должно существовать строгой линейной зависимости между переменными Х1, X3,..., Хk.

Первая гипотеза означает, что переменные ui, имеют нулевую среднюю.

Суть гипотезы  в том, что все случайные ошибки ui, имеют постоянную дисперсию, то есть выполняется условие гомоскедастичности дисперсии.

МНК заключается в минимизации функционала:

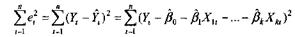
т.е. обращения в нуль частных производных по каждому из параметров:

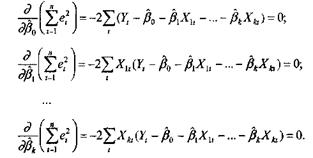
Упростив последние равенства, получим стандартную форму нормальных уравнений, решение которых дает искомые оценки параметров:

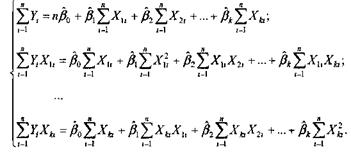
Сложность решения системы линейных уравнений с (k+1) неизвестными увеличивается быстрее, чем растет k. В зависимости от количества уравнений система может быть решена методом исключения Гаусса или методом Крамера или другим численным методом решения системы линейных алгебраических уравнений.

Поскольку для большинства практических задач изучаются несколько альтернативных спецификаций модели, то широкое применение ЭВМ, а также специальных статистических пакетов позволяет значительно упростить процедуру оценивания.

Возможна и другая запись уравнения модели в так называемом стандартизованном масштабе:

где ty, tx1 ,..., tхk - стандартизованные переменные:

для которых среднее значение равно нулю:

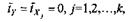
а среднее квадратическое отклонение равно единице:

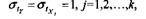
bj, j=1,2,…k - стандартизованные коэффициенты регрессии.

Нетрудно установить зависимость между коэффициентами "чистой" регрессии Bj и стандартизованными коэффициентами регрессии bj, j=1,2,…k, а именно:


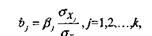
причем

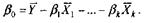
Стандартизованные коэффициенты регрессии показывают, на сколько "сигм" изменится в среднем результат (Y), если соответствующий фактор Хj изменится на одну "сигму" при неизменном среднем уровне других факторов.

В силу того, что все переменные центрированы и нормированы, коэффициенты bj, j=1,2,…k, сравнимы между собой (в этом их отличие от Вj) Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат, что позволяет произвести отсев факторов - исключить из модели факторы с наименьшими значениями bj.

Нетрудно показать, что оценки МНК Bj, j=0,2,…k являются наиболее эффективными (в смысле наименьшей дисперсии) оценками в классе линейных несмещенных оценок (теорема Гаусса-Маркова).

Как было уже указано раньше, достоинством метода множественной регрессии является возможность выделения влияния каждого из факторов Хj в условиях, когда воздействие многих переменных на результат эксперимента не удается контролировать. Степень раздельного влияния каждого из факторов характеризуется оценками Bj, j=0,2,…k.

Для определения параметров модели по методу Койка уравнение авторегрессии можно специфицировать как:

  

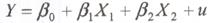
Следовательно, система нормальных уравнений для модели Койка  будет иметь вид


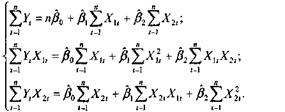
2.5 Алгоритм работы программы:


1)    Запуск программы

2)    Загрузка данных по временному ряду из файла Microsoft Excel установленного образца (см. Описание формата входного файла) в массив данных.

3)    Вычисление параметров модели.

3.1. Формируем данные для y(t-1). Получаем двухфакторную модель авторегрессии yt(x,yt-1);

3.2. Для определения параметров модели по методу Койка рассмотрим ее как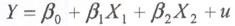

и определим параметры, решив методом наименьших квадратов (МНК) следующую систему уравнений:

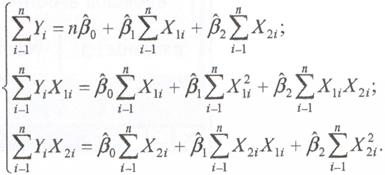
3.3. От полученных результатов МНК получаем параметры модели по формулам

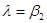
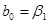
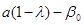
3.4. Формируем столбец оценочных результатов.

3.5. Вычисляем средний, медианный лаг, дисперсию.

Вывод на экран результатов.

2.6 Описание формата входного файла

Для загрузки данных временного ряда в программу данные должны быть сформированы в формате Microsoft Excel в следующем виде:

1.     Загружаются только первые 3 столбца (A, B, C).

- столбец A – Название временного периода, момент времени

- столбец B – Значение результирующего показателя

- столбец C – Значение влияющего показателя

2.     Первая строка - заголовок столбцов;

3.     Данные должны быть представлены в числовом виде.

4.     Лист данными должен быть сохранен как активный.

Пример входного файла представлен в приложении 1.

3 Программная система построение моделей распределенных лагов на основе метода Койка и тестовые примеры.

3.1 Анализ тестового примера 1

 

Y

X

1

-0,009308331

-0,002581811

2

0,000211741

0,00304921

3

-0,020436603

-0,031319769

4

-0,011248105

-0,025688747

5

-0,022215494

-0,040057726

6

-0,003329578

-0,014426705

7

-0,014579355

-0,038795684

8

0,004047851

-0,013164662

9

0,022566232

0,012466359

10

0,030991324

0,01809738

11

0,009339812

-0,016271598

12

0,027629326

0,009359423

13

-0,014121777

-0,025009556

14

-0,035894637

-0,049378535

15

-0,01767013

-0,033747513

16

0,000570906

0,031883508

17

-0,031152575

0,007514529

18

-0,012822056

0,033145551

19

-0,024419683

0,038776572

20

-0,025928493

0,004407593

21

-0,027332614

3,86145E-05

22

-0,008617467

0,025669636

23

-0,019769945

0,021300657

24

-0,030778572

-0,013068322

25

-0,021633646

0,0025627

26

-0,022327359

0,008193721

27

-0,012853895

0,013824742

28

-0,003209497

0,019455764

29

0,006607483

0,025086785

30

-0,003403436

0,000717806

31

-0,003244858

-0,003651173

32

0,007078524

0,011979849

33

0,007559984

0,00761087

34

-0,011809154

-0,016758109

35

-0,011039409

-0,011127087

36

-0,020143011

-0,015496066

37

0,000866246

-0,009865045

38

0,021973178

0,025765976

39

0,003161394

0,021396998

40

0,024413502

0,057028019

41

0,015711322

0,05265904

42

-0,002963889

0,048290062

43

-0,021631209

0,023921083

44

-0,020309811

0,019552104

45

-0,009018729

0,025183125

46

0,012223374

0,030814147

47

0,013398444

0,046445168

48

-0,025510751

0,022076189

49

-0,034520401

0,007707211

50

-0,013645459

-0,006661768

51

0,007100548

0,008969253

52

-0,012294319

-0,015399726

53

-0,031840261

-0,009768704

54

-0,011545616

-0,034137683

55

-0,001416756

-0,028506662

56

-0,031458007

-0,06287564

57

-0,0316716

-0,067244619

58

-0,052057637

-0,081613598

59

-0,042614096

-0,045982577

60

-0,033336852

-0,030351555

61

-0,004219729

-0,004720534

62

0,004745424

0,010910487

63

0,003568632

0,026541509

64

0,012261669

0,02217253

65

0,020837917

0,017803551

66

-0,000687803

-0,006565428

67

0,017700588

0,022065594

68

-0,013979773

-0,015303385

69

-0,015710899

-0,009672364

70

-0,017474178

-0,034041342

71

0,000749398

0,011589679

72

0,018979

0,0172207

По результатам работы программы на тестовом примере были получены следующие результаты:

Параметры модели:

l=0.4009

a=-0.0077

b0=0.2875

Дополнительные параметры:

Средний лаг=0.6693

Медианный лаг=0.7584

Дисперсия = 0.0119

В данной модели темп уменьшения лаговых воздействий достаточно низок, поэтому на текущие параметры оказывает существенное влияние и результаты предыдущих значений.  В среднем воздействие показателя X на показатель Y проявляется в течении 0,6693 единиц времени при этом половина этого воздействия реализуется в течении 0,7584 ед.

3.2 Анализ тестового примера 2

 

y

x

1

0,11

0,2

2

0,22

0,354

3

0,356

0,231

4

0,3215

0,25479

5

0,245

0,654

6

0,65

0,4987

7

0,321

0,6842

8

0,845

0,2457

9

0,6987

0,321

10

0,235

0,2354

11

0,357

0,536

12

0,987

0,0025

По результатам работы программы на тестовом примере были получены следующие результаты:

Параметры модели:

l=0,1038

a=0,7580

b0=-0,6695

Дополнительные параметры:

Средний лаг=0,1159

Медианный лаг=0,3060

Дисперсия = 0,1464

В данной модели темп уменьшения лаговых воздействий достаточно низок, поэтому на текущие параметры оказывает существенное влияние и результаты предыдущих значений.  В среднем воздействие показателя X на показатель Y проявляется в течении 0,1159 единиц времени при этом половина этого воздействия реализуется в течении 0,3060 ед. времени.


3.3 Анализ тестового примера 3

 

y

x

1

0,965

0,2

2

0,9874

0,354

3

0,564

0,231

4

0,123

0,25479

5

0,023

0,654

6

0,012

0,4987

7

0,021

0,6842

8

0,009

0,2457

9

0,008

0,321

10

0,007

0,2354

11

0,006

0,536

12

0,005

0,0025

13

0,004

0,07515

14

0,002

0,0002

15

0

-0,0747

16

-0,002

-0,1497

17

-0,004

-0,2246

18

-0,006

-0,2996

19

-0,008

-0,3745

По результатам работы программы на тестовом примере были получены следующие результаты:

Параметры модели:

l=0,7209

a=-0,0417

b0=-0,001

Дополнительные параметры:

Средний лаг=2,5836

Медианный лаг=2,1185

Дисперсия = 0,0088

В среднем воздействие показателя X на показатель Y проявляется в течении 2,5836 единиц времени при этом половина этого воздействия реализуется в течении 2,1185 ед. времени.


ЗАКЛЮЧЕНИЕ


Исследованный метод Койка является одним из базовых методов эконометрики для моделей с распределенным лагом и моделей авторегрессии. Его можно использовать для получения достаточно точных моделей с распределенным лагом и применять на практике.

По результатам дипломной работы был получен программный продукт, разработанный в среде Borland Delphi, позволяющий без значительных аппаратных затрат производить вычисление параметров авторегрессии по методу Койка, считать медианный и средний лаги. При этом был создан интуитивно понятный интерфейс для работы с программой, не предъявляющий особых требований к квалификации оператора. Применение данного программного продукта на практике позволит значительно облегчить вычислительный труд при использовании в моделировании метода Койка.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ


1   Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики -М   ЮНИТИ, 1998 - 1022с 13ВМ 5-238-00013-8

2   Доугерти К. Введение в эконометрику - М   ИНФРА-М, 1997 - XIV, 402 с ил   - (Университетский учебник) Библиография   с 384-386   15ВМ 5-86225-458-7, 0-19-50346-4

3   Елисеева И.И. Эконометрика Учебник /И И Елисеева и др - М   Финансы и статистика, 2001 - 15ВК 5-279-01955-0

4   Князевский В.С., Житников И.В. Анализ временных рядов и прогнозирование Учеб пособие -Ростов-на-Дону РГЭА, 1998 - 161 с

5   Князевский В.С., Молчанов И.Н. Статистические расчеты на компьютере с использованием ППП Microstat - Ростов-на-Дону РГЭА, 1996 - 86 с

6   Кремер Н., Прутко Б. Эконометрика. М.: БНИТИ-ДАНА, 2002. 311 с.

7   Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика  Начальный курс - М   Дело, 2000 - 400 с 13ВК 5-7749-0055-Х

8   Практикум по эконометрике Учеб пособие /И И Елисеева и др - М   Финансы и статистика, 2001 - 192 с 18ВК 5-279-02313-2

ПРИЛОЖЕНИЕ 1 - Пример входного файла


 

Y

X

1

-0,009308331

-0,002581811

2

0,000211741

0,00304921

3

-0,020436603

-0,031319769

4

-0,011248105

-0,025688747

5

-0,022215494

-0,040057726

6

-0,003329578

-0,014426705

7

-0,014579355

-0,038795684

8

0,004047851

-0,013164662

9

0,022566232

0,012466359

10

0,030991324

0,01809738

11

0,009339812

-0,016271598

12

0,027629326

0,009359423

13

-0,014121777

-0,025009556

14

-0,035894637

-0,049378535

15

-0,01767013

-0,033747513

16

0,000570906

0,031883508

17

-0,031152575

0,007514529

18

-0,012822056

0,033145551

19

-0,024419683

0,038776572

20

-0,025928493

0,004407593

21

-0,027332614

3,86145E-05

22

-0,008617467

0,025669636

23

-0,019769945

0,021300657

24

-0,030778572

-0,013068322

25

-0,021633646

0,0025627

26

-0,022327359

0,008193721

27

-0,012853895

0,013824742

28

-0,003209497

0,019455764

29

0,006607483

0,025086785

30

-0,003403436

0,000717806

31

-0,003244858

-0,003651173

32

0,007078524

0,011979849

33

0,007559984

0,00761087

34

-0,011809154

-0,016758109

35

-0,011039409

-0,011127087

36

-0,020143011

-0,015496066

37

0,000866246

-0,009865045

38

0,021973178

0,025765976

39

0,003161394

0,021396998

40

0,024413502

0,057028019

41

0,015711322

0,05265904

42

-0,002963889

0,048290062

43

-0,021631209

0,023921083

44

-0,020309811

0,019552104

45

-0,009018729

0,025183125

46

0,012223374

0,030814147

47

0,013398444

0,046445168

48

-0,025510751

0,022076189

49

-0,034520401

0,007707211

50

-0,013645459

-0,006661768

51

0,007100548

0,008969253

52

-0,012294319

-0,015399726

53

-0,031840261

-0,009768704

54

-0,011545616

-0,034137683

55

-0,001416756

-0,028506662

56

-0,031458007

-0,06287564

57

-0,0316716

-0,067244619

58

-0,052057637

-0,081613598

59

-0,042614096

-0,045982577

60

-0,033336852

-0,030351555

61

-0,004219729

-0,004720534

62

0,004745424

0,010910487

63

0,003568632

0,026541509

64

0,012261669

0,02217253

65

0,020837917

0,017803551

66

-0,000687803

-0,006565428

67

0,017700588

0,022065594

68

-0,013979773

-0,015303385

69

-0,015710899

-0,009672364

70

-0,017474178

-0,034041342

71

0,000749398

0,011589679

72

0,018979

0,0172207

ПРИЛОЖЕНИЕ 2 – ЛИСТИНГ ПРОГРАММЫ.


program Koyck;


uses

  Forms,

  Unit1 in 'Unit1.pas' {Main};


{$R *.RES}


begin

  Application.Initialize;

  Application.Title := 'Метод Койка';

  Application.CreateForm(TMain, Main);

  Application.Run;

end.


unit Unit1;


interface


uses

  Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,

  Buttons, StdCtrls, Grids,ComObj, ActiveX;


type

  TMain = class(TForm)

    Label1: TLabel;

    source: TStringGrid;

    Label3: TLabel;

    Load: TButton;

    GroupBox1: TGroupBox;

    Label2: TLabel;

    Edit1: TEdit;

    Label4: TLabel;

    Edit2: TEdit;

    Label5: TLabel;

    Edit3: TEdit;

    GroupBox2: TGroupBox;

    Label6: TLabel;

    Label7: TLabel;

    Label8: TLabel;

    Edit4: TEdit;

    Edit5: TEdit;

    Edit6: TEdit;

    Calc: TButton;

    Quit: TBitBtn;

    OpenFile: TOpenDialog;

    procedure QuitClick(Sender: TObject);

    procedure LoadClick(Sender: TObject);

    procedure CalcClick(Sender: TObject);

  private

    { Private declarations }

  public

    { Public declarations }

  end;


type

  TRow = record

    Y: real;

    X1: real;

    X2: real;

    Y_2: real;

    X1_2: real;

    X2_2: real;

    X1Y: real;

    X2Y: real;

    X1X2: real;

    Y_oc:real;

    e:real;

  end;

  TMatrix=array[0..2,0..3] of real;

const

  MAX_ROWS=100;

  STEP=0.01;

var

  Main: TMain;

  mas: array[0..MAX_ROWS] of TRow; //Рабочий массив массив

  Sum: TRow; //Суммы столбцов

  n_rows: integer;  //Вспомогательные переменные

  lamda,a,b0,Disp: real;

  X1_sr,X2_sr,Y_sr,Y_oc_sr, sig_Y, sig_X1, sig_X2: real;

  m: TMatrix;

implementation


{$R *.DFM}


Procedure Gauss(var c:TMatrix);

  var i,j,k,n:integer;

  s: real;

begin

  n:=2;

  s:=0;

  for k:=0 to n do begin

    s:=C[k,k];

    for j:=k to n+1 do C[k,j]:=C[k,j]/s;

    for i:=k+1 to n do

      begin

      s:=C[i,k];

      for j:=k to n+1 do

        C[i,j]:=C[i,j]-s*C[k,j];

      end;

  end;

  for i:=n-1 downto 0 do

  begin

    s:=0;

    for j:=i+1 to n do s:=s+ C[i,j]*C[j,n+1];

    c[i,n+1]:=C[i,n+1]-s;

  end;

end;


procedure TMain.QuitClick(Sender: TObject);

begin

 close;

end;


procedure TMain.LoadClick(Sender: TObject);

var i,j,Err: integer;

    WBk:OleVariant;

    Excel: Variant;

    s: string;

begin

  Err:=0;

  if OpenFile.Execute then //Запрашиваем имя файла

    begin

      Excel := CreateOleObject('Excel.Application');

      Excel.Visible := false;

      Wbk := Excel.WorkBooks.Open(OpenFile.FileName);


      //Определяем число строк

      i:=0; j:=1;

       while (i<2) and (Err=0) do

          begin

            s:=Excel.ActiveSheet.Cells.Item[j,1].Value;

            if length(s)=0 then i:=i+1

              else

                if i>1 then

                  begin

                    MessageDlg('Неправильный формат файла',mtError,[mbok],0);

                    Err:=1;

                  end;

              j:=j+1;

          end;

        n_rows:=j-4;

        if n_rows>MAX_ROWS then n_rows:=MAX_ROWS;


        //Загружаем название

        for j:=1 to 3 do

           source.Cells[j-1,0] := Excel.ActiveSheet.Cells.Item[1,j].Value;

        source.Cells[3,0] :='y(t-1)';

        for i:=1 to n_rows+2 do

           source.Cells[0,i-1] := Excel.ActiveSheet.Cells.Item[i,1].Value;


       //Загружаем данные

       for i:=2 to N_rows+2 do

         begin

         try

           mas[i-2].Y:=StrToFloat(Excel.ActiveSheet.Cells.Item[i,2].Value);

         except

           on EConvertError do

             begin

               mas[i-2].Y:=0;

             end;

           on EVariantError do

             begin

               mas[i-2].Y:=0;

             end;

         end;

         try

           mas[i-2].X1:=StrToFloat(Excel.ActiveSheet.Cells.Item[i,3].Value);

         except

           on EConvertError do

             begin

               mas[i-2].X1:=0;

             end;

           on EVariantError do

             begin

               mas[i-2].X1:=0;

             end;

         end;

         if i>2 then mas[i-2].X2:=mas[i-3].Y;

         end;

       WBk.Close(SaveChanges := false);

       Excel.Quit;


  //n_rows:=20;


  {mas[0].Y:=51;    mas[0].X1:=35;   mas[0].X2:=0;

  mas[1].Y:=16;    mas[1].X1:=16;   mas[1].X2:=51;

  mas[2].Y:=74;    mas[2].X1:=18;   mas[2].X2:=16;

  mas[3].Y:=7.5;   mas[3].X1:=2;    mas[3].X2:=74;

  mas[4].Y:=33;    mas[4].X1:=14;   mas[4].X2:=7.5;

  mas[5].Y:=26;    mas[5].X1:=33;   mas[5].X2:=33;

  mas[6].Y:=11.5;  mas[6].X1:=20;   mas[6].X2:=26;

  mas[7].Y:=52;    mas[7].X1:=25;   mas[7].X2:=11.5;

  mas[8].Y:=15.8;  mas[8].X1:=13;   mas[8].X2:=52;

  mas[9].Y:=8;     mas[9].X1:=2;    mas[9].X2:=15.8;

  mas[10].Y:=26;   mas[10].X1:=21;  mas[10].X2:=8;

  mas[11].Y:=6;    mas[11].X1:=11;  mas[11].X2:=26;

  mas[12].Y:=5.8;  mas[12].X1:=3;   mas[12].X2:=6;

  mas[13].Y:=13.8; mas[13].X1:=3.5; mas[13].X2:=5.8;

  mas[14].Y:=6.2;  mas[14].X1:=2.8; mas[14].X2:=13.8;

  mas[15].Y:=7.9;  mas[15].X1:=17;  mas[15].X2:=6.2;

  mas[16].Y:=5.4;  mas[16].X1:=3.4; mas[16].X2:=7.9;

  mas[17].Y:=56;   mas[17].X1:=24;  mas[17].X2:=5.4;

  mas[18].Y:=25.5; mas[18].X1:=9;   mas[18].X2:=56;

  mas[19].Y:=7.1;  mas[19].X1:=4.5; mas[19].X2:=25.5;

}


  source.RowCount:=n_rows+2;

  for I := 0 to n_rows do

    begin

      source.Cells[1,I+1] := FloatToStr(mas[i].Y);

      source.Cells[2,I+1] := FloatToStr(mas[i].X1);

      source.Cells[3,I+1] := FloatToStr(mas[i].X2);

    end;


  Sum.Y:=0;

  Sum.X1:=0;

  Sum.X2:=0;

  Sum.Y_2:=0;

  Sum.X1_2:=0;

  Sum.X2_2:=0;


  for i:=1 to n_rows do

    begin

      Sum.Y:=Sum.Y+mas[i].Y;

      Sum.X1:=Sum.X1+mas[i].X1;

      Sum.X2:=Sum.X2+mas[i].X2;


      mas[i].Y_2:=mas[i].Y*mas[i].Y;

      mas[i].X1_2:=mas[i].X1*mas[i].X1;

      mas[i].X2_2:=mas[i].X2*mas[i].X2;


      Sum.Y_2:=Sum.Y_2+mas[i].Y_2;

      Sum.X1_2:=Sum.X1_2+mas[i].X1_2;

      Sum.X2_2:=Sum.X2_2+mas[i].X2_2;

     

      mas[i].X1Y:=mas[i].X1*mas[i].Y;

      mas[i].X2Y:=mas[i].X2*mas[i].Y;

      mas[i].X1X2:=mas[i].X1*mas[i].X2;


      Sum.X1Y:=Sum.X1Y+mas[i].X1Y;

      Sum.X2Y:=Sum.X2Y+mas[i].X2Y;

      Sum.X1X2:=Sum.X1X2+mas[i].X1X2;

    end;


  Y_sr:=Sum.Y/(n_rows-1);

  X1_sr:=Sum.X1/(n_rows-1);

  X2_sr:=Sum.X2/(n_rows-1);


  m[0][0]:=n_rows;      m[0][1]:=Sum.X1;        m[0][2]:=Sum.X2;        m[0][3]:=Sum.Y;

  m[1][0]:=Sum.X1;      m[1][1]:=Sum.X1_2;      m[1][2]:=Sum.X1X2;      m[1][3]:=Sum.X1Y;

  m[2][0]:=Sum.X2;      m[2][1]:=Sum.X1X2;      m[2][2]:=Sum.X2_2;      m[2][3]:=Sum.X2Y;

  end;

end;


procedure TMain.CalcClick(Sender: TObject);

var i: integer;

    s: real;

begin


  Gauss(m);

  lamda:=m[2,3];

  b0:=m[1,3];

  if lamda=1 then a:=0 else a:=m[0,3]/(1-m[2,3]);

  source.ColCount:=5;

  source.Cells[4,0] := 'Y_oc';

  mas[1].Y_oc:=a*(1-lamda)+b0*mas[1].X1;

  source.Cells[4,2] :=FloatToStr(mas[1].Y_oc);

  Sum.Y_oc:=Sum.Y_oc+ mas[1].Y_oc;

  for i:=2 to n_rows do

    begin

      mas[i].Y_oc:=a*(1-lamda)+b0*mas[i].X1+lamda*mas[i-1].Y_oc;

      source.Cells[4,i+1] :=FloatToStr(mas[i].Y_oc);

      Sum.Y_oc:=Sum.Y_oc + mas[i].Y_oc;

    end;


  Y_oc_sr:=Sum.Y_oc/(n_rows-1);

  s:=0;

  for i:=1 to n_rows do

    s:=s+sqr(mas[i].Y_oc-Y_oc_sr);

  Disp:=sqrt(s/(n_rows-1));

  edit1.Text:=FloatToStr(lamda);

  edit2.Text:=FloatToStr(a);

  edit3.Text:=FloatToStr(b0);

  if lamda<>1 then edit4.Text:=FloatToStr(lamda/(1-lamda));

  if (lamda>0) and (lamda<1) then

    edit5.Text:=FloatToStr(ln(0.5)/ln(lamda));

  edit6.Text:=FloatToStr(Disp);

end;


end.