Задача 1.3.
Некоторая
фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В
обычный набор входит 3 кг
азотных, 4 кг
фосфорных и 1 кг
калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений.
Известно, что для некоторого газона требуется,
по меньшей мере 10 кг
азотных, 20 кг
фосфорных и 7 кг
калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный – 4 ден.
ед. Какие и сколько наборов удобрений
нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать
стоимость?
Построить экономико-математическую
модель задачи, дать необходимые комментарии к ее элементам и получить решение
графическим методом. Что произойдет, если решать задачу на максимум и почему?
Задача 2.3.
Для изготовления четырех видов продукции
используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации
единицы каждого вида продукции приведены в таблице 1.
|
Тип
сырья
|
Нормы
расхода сырья на одно изделие
|
Запасы
сырья
|
|
А
|
Б
|
В
|
Г
|
І
ІІ
ІІІ
|
2
1
2
|
1
2
4
|
3
4
1
|
2
8
1
|
200
160
170
|
|
Цена
изделия
|
5
|
7
|
3
|
6
|
|
Таблица
1
Требуется:
1.
Сформулировать
прямую оптимизационную задачу на максимум выручки от реализации готовой
продукции, получить оптимальный план выпуска продукции.
2.
Сформулировать
двойственную задачу и найти ее оптимальный план с помощью теорем
двойственности.
3.
Поясните
нулевые значения переменных в оптимальном плане.
4.
На
основе свойств двойственных оценок и
теорем двойственности:
·
Проанализировать
использование ресурсов в оптимальном плане исходной задачи;
·
Определить,
как изменяется выручка от реализации продукции и план ее выпуска при увеличении
запасов сырья І и ІІ видов на 8 и 10 единиц
соответственно и уменьшении на 5 единиц запасов сырья ІІІ вида;
·
Оценить
целесообразность включения в план изделия Д ценой 10 единиц, на изготовление
которого расходуется по две единицы каждого вида сырья.
Задача 3. Используя
балансовый метод планирования и модель Леонтьева построить баланс производства
и распределения продукции предприятий.
Задачи 3.1-3.10.
Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при
этом каждое из трех предприятий группы специализируется на выпуске продукции
одного вида: первое предприятие специализируется на выпуске продукции первого
вида, второе предприятие - продукции второго вида; третье предприятие -
продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями
холдинга (идет на внутреннее потребление), остальная часть поставляется за его
пределы (внешним потребителям, является конечным продуктом). Специалистами
управляющей компании получены экономические оценки аij (i=1,2,3; j=1,2,3) элементов технологической
матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов
yi
вектора конечной продукции Y.
Требуется:
1) Проверить
продуктивность технологической матрицы A=(аij) (матрицы коэффициентов прямых материальных затрат).
2) Построить баланс
(заполнить таблицу) производства и
распределения продукции предприятий холдинга.
В
соответствии с номером Вашего варианта ниже в таблице 3 выберите числовые
значения для таблицы 4.
Задача 4. Исследовать динамику экономического показателя на основе
анализа одномерного временного ряда.
Задачи 4.1-4.10. В течение девяти последовательных недель фиксировался
спрос Y(t)
(млн. р.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя
(повариантно) приведен ниже в таблице
Номер варианта
|
Номер наблюдения ( t =
1,2,…,9)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
3
|
3
|
7
|
10
|
11
|
15
|
17
|
21
|
25
|
23
|
Требуется:
1)
Проверить наличие аномальных наблюдений.
2)
Построить линейную модель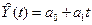 
, параметры которой
оценить МНК (
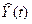- расчетные,
смоделированные значения временного ряда).
3)
Оценить адекватность построенных моделей, используя свойства независимости
остаточной компоненты, случайности и соответствия нормальному закону
распределения (при использовании R/S-критерия взять табулированные границы
2,7—3,7).
4)
Построить адаптивную модель Брауна[1]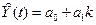 
с параметром сглаживания
a= 0,4 и a= 0,7; выбрать лучшее значение параметра сглаживания α.
5)
Оценить адекватность построенных моделей, используя свойства независимости
остаточной компоненты, случайности и соответствия нормальному закону
распределения (при использовании R/S-критерия взять табулированные границы
2,7—3,7).
6)
Оценить точность моделей на основе использования средней относительной ошибки
аппроксимации.
7) По
двум построенным моделям осуществить прогноз спроса
на следующие две недели (доверительный
интервал прогноза рассчитать при доверительной вероятности р = 70%).
8)
Фактические значения показателя, результаты моделирования и прогнозирования
представить графически.
РЕШЕНИЕ
Задача 1.3.
Составим
экономико-математическую модель.
І набор
– обычный
ІІ набор
– улучшенный Таблица 3
|
Удобрения
|
Необходимый min для 1 газона
|
Число кг в 1 наборе
|
|
І
|
ІІ
|
|
Азотные
|
10
|
3
|
2
|
|
Фосфорные
|
20
|
4
|
6
|
|
Калийные
|
7
|
1
|
3
|
Обычный
набор стоит 3 ден. Ед., а улучшенный – 4 ден. Ед.
Обозначим
через X и Y количество обычных и улучшенных наборов удобрений, соответственно.
1.
Составим
целевую функцию и систему ограничений.
_
F( x) = 3x + 4y → min
Система
ограничений:
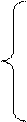3x + 2y ≥ 10; (1)
4x + 6y ≥ 20; (2)
x + 3y ≥ 7; (3)
x, y ≥ 0;
2.
По
ограничениям строим область всех допустимых решений.
А) Определим
множество решений 1-го неравенства. Построим линию по точкам: (0;5) и (2;2). Т. К. 3 * 0 + 2 * 0 = 0 < 10 , то выбираем верхнюю полуплоскость.
Б) Определим множество решений 2-го неравенства.
Построим линию по точкам: (5;0) и (2;2). Т. К. 4 * 0 + 6 * 0 = 0 < 20 , то
выбираем верхнюю полуплоскость.
В) Определим множество решений 3-го неравенства. Построим линию по
точкам: (7;0) и (1;2). Т. К. 1*
0 + 3 * 0 = 0 < 7, то выбираем
верхнюю полуплоскость.
3.
Пересечением всех плоскостей является неограниченная
область ABCDEF (рис.1).
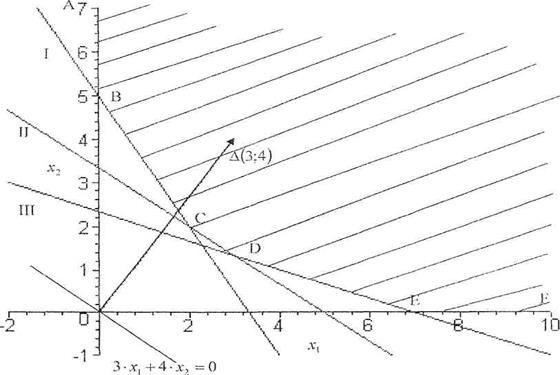
Рис.1
4. Для
определения направления движения к оптимуму построим вектор-градиент, соединив
его вершину ∆(3;4) с началом координат.
5.
Построим линию уровня 3x +4 y =0 по точкам: (0;0) и (4;-3).
Она перпендикулярна вектору- градиенту.
6.
При минимизации целевой функции необходимо перемещать
линию уровня в направлении, противоположном вектору-градиенту. Точкой максимума при таком движении линии
уровня будет точка С (2;2), а
минимальное значение функции Fmin = F(2;2) =3 * 2 + 4 * 2 = 14 ден. ед.
Ответ: 2
обычных и 2 улучшенных набора удобрений для газонов нужно купить, чтобы минимизировать
стоимость.
Построенная область допустимых решений не ограничена
сверху, следовательно, если задачу решать на max, то f(max)= ∞, т.е. не имеет конечного оптимума, т.к.
область допустимых значений не ограничена сверху.
Задача 2.3.
Сформулируем прямую оптимизационную задачу:
_
F(x) = 5x1 + 7x2 + 3x3
+ 6x4 → max
Система ограничений:
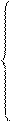2x1 + x2 + 3x3 + 2x4 ≤ 200,
x1
+ 2x2 + 4x3 + 8x4 ≤ 160,
2x1 + 4x2 + x3 + x4
≤ 170,
x1,
2, 3, 4 ≥ 0
Воспользуемся командой
Поиск решения (в меню Сервис). Заполним окно Поиск решения, как на рис. 2. В
окне Поиск решения нажать на кнопку выполнить. Через непродолжительное время
появится диалоговое окно Результаты поиска решения и исходная таблица с
заполненными ячейками В2:Е2 для значений Хj и ячейка G2 с максимальным значением целевой
функции (рис. 3).
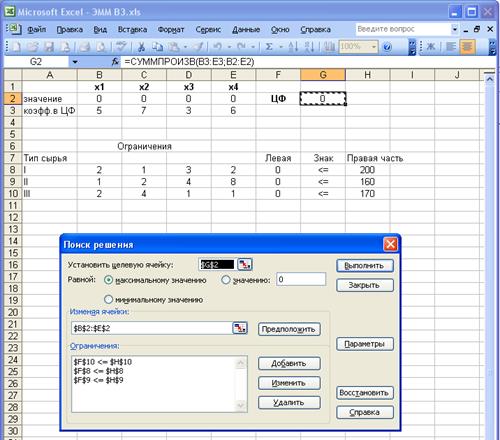
Рис. 2
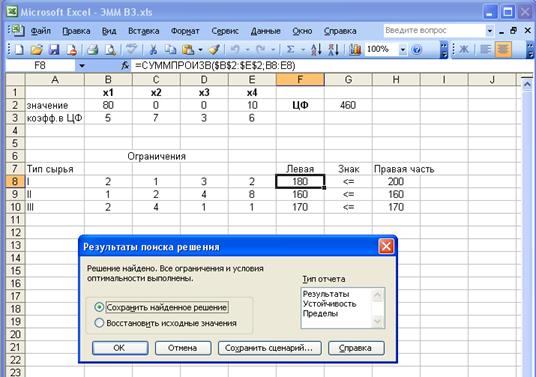
Рис.3
Оптимальное решение задачи: x1 = 80; x2 = 0;
x3 = 0; x4 = 10;
Fmax = 5 * 80 + 7 * 0 + 3 * 0 + 6 * 10
=460 ден. ед.
По оптимальному плану следует
производить изделия типа А и Г. Изделия типа Б и В убыточны, затраты на ресурсы
превышают цену изготовления из них изделий.
Excel позволяет представить результаты поиска решения в форме отчета (рис. 4):
|
Microsoft Excel 11.0 Отчет по
результатам
|
|
|
|
|
Целевая ячейка (Максимум)
|
|
|
|
|
Ячейка
|
Имя
|
Исходное значение
|
Результат
|
|
|
|
|
$G$2
|
ЦФ
|
460
|
460
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изменяемые ячейки
|
|
|
|
|
|
|
Ячейка
|
Имя
|
Исходное значение
|
Результат
|
|
|
|
|
$B$2
|
значение х1
|
80
|
80
|
|
|
|
|
$C$2
|
значение х2
|
0
|
0
|
|
|
|
|
$D$2
|
значение х3
|
0
|
0
|
|
|
|
|
$E$2
|
значение х4
|
10
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ограничения
|
|
|
|
|
|
|
Ячейка
|
Имя
|
Значение
|
Формула
|
Статус
|
Разница
|
|
|
$F$8
|
I Левая
|
180
|
$F$8<=$H$8
|
не связан.
|
20
|
|
|
$F$9
|
II Левая
|
160
|
$F$9<=$H$9
|
связанное
|
0
|
|
|
$F$10
|
III Левая
|
170
|
$F$10<=$H$10
|
связанное
|
0
|
|
|
Рис.4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сформулируем двойственную задачу и
найдем ее оптимальный план.
G(y) = 200 y1 + 160 y2 +
170 y3
→min
Система ограничений:
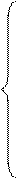2 y1
+ y2 + 2 y3 ≥ 5;
y1 + 2 y2 + 4 y3 ≥ 7;
3
y1 + 4 y2 + y3
≥ 3;
2
y1 + 8 y2 + y3 ≥ 6;
y1, 2, 3, ≥ 0
Координаты Xmax подставляем в 1 систему. Получаем:
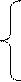2 * 8 0
+ 0 +
3 * 0 + 2
* 10 = 180
< 200,
80 + 2 * 0 + 4 * 0 + 8 * 10=160,
2 * 80 + 4 * 0 + 0 +
10 = 170.
Первое ограничение выполняется как строгое неравенство.
Поэтому, y1 = 0 (по второй
теореме двойственности).
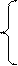Т.к. х1 > 0 и х4
> 0, то
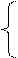
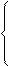2y1 + y2 + 2y3 =
5; 0 + y2 + 2y3 =
5; y3 = 34/15;
2y1 + 8y2 + y3 = 6 0 + 8y2 +y3 = 6 y2 = 7/15
Y оптим. = (0; 7/15; 34/15)
При подстановке Y оптим. в целевую функцию получается, что
G min = 200 * 0 + 160 * 7/15 + 170 * 34/15
= 460.
Проанализируем
использование ресурсов в оптимальном плане.
Недефицитным оказалось сырье I типа, поскольку y1 = 0. Острее ощущается дефицитность сырья III типа (yз =34/15), чем сырья II типа (y2 =7/15). Увеличение
запаса сырья II и III типа на 1 ед. приведет
к росту прибыли, изменение запаса сырья I типа не влияет
на выручку.
Определим, как
изменятся общая стоимость продукции и план ее выпуска при увеличении запасов
сырья I и II видов на 8 и 10 ед. соответственно и уменьшении на 5 ед. запасов сырья III вида.
Допустим, что
изменения проходят в
пределах устойчивости двойственных
оценок, т.е. структура оптимального плане не
изменится и х2 = х3
= 0
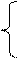
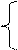
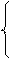x1 + 2x2 + 4x3 + 8x4 = 160+10, x1 +8x4 =170 , х4 =
35/3,
2х1 +4x2 ++ x3 + х4 = 170 – 5. 2x1 + x4 = 165. x1 = 230/3
Fmax = 5*230/3 + 7*0
+ 3*0 + 6*35/3 = 1360/3
Выручка уменьшилась на 460 -1360/3=20/3 ден.
ед.
Определим
целесообразность включения в план изделия «Д» ценой 10 ден. ед., на
изготовление которого расходуется по две единицы каждого
вида сырья.
Вычислим ∆ = 2*0 + 2*7/15 +
2*34/15*10 = - 68/15
< 0, т.е. затраты на производство данного изделия не превышают его цену, следовательно, включать
такое изделие в план целесообразно.
Задача 3.
Таблица 3
|
Вариант
|
Для первой строки
|
Для второй строки
|
Для третьей строки
|
|
3
|
0,2
|
0,1
|
0,2
|
150
|
0,0
|
0,1
|
0,2
|
180
|
0,1
|
0,0
|
0,1
|
100
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4
Предприятия
(виды продукции)
|
Коэффициенты прямых затрат аi j
|
Конечный
продукт Y
|
|
1
|
2
|
3
|
1
2
3
|
1А
1Б
1В
|
2А
2Б
2В
|
3А
3Б
3В
|
4А
4Б
4В
|
1) Проверить продуктивность технологической матрицы A=(аij) (матрицы коэффициентов прямых
материальных затрат).
1.1. Заполним таблицу 5 данными:
Таблица 5
Исходные данные
Предприятия
(виды продукции)
|
Коэффициенты прямых затрат аi j
|
Конечный
продукт Y
|
|
1
|
2
|
3
|
1
2
3
|
0,2
0,0
0,1
|
0,1
0,1
0,0
|
0,2
0,2
0,1
|
150
180
100
|
1.2. Для решения данной экономической задачи будет выбрана
среда табличного процессора MS Excel. (таблица 6)
Таблица 6
|
Предприятия (виды продукции)
|
Коэффициенты прямых затрат aij
|
Конечный продукт Y
|
|
1
|
2
|
3
|
|
1
|
0,2
|
0,1
|
0,2
|
150
|
|
2
|
0,0
|
0,1
|
0,2
|
180
|
|
3
|
0,1
|
0,0
|
0,1
|
100
|
|
|
|
|
|
|
|
|
|
|
|
0,2
|
0,1
|
0,2
|
|
|
A =
|
0,0
|
0,1
|
0,2
|
|
|
0,1
|
0,0
|
0,1
|
|
|
|
|
|
|
1.3. Найдем разность между единичной матрицей Е и матрицей А.
Для этого воспользуемся правилом
вычитания матриц одинаковой размерности.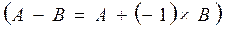 
(таблица 7)
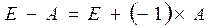
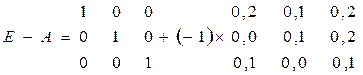
Таблица 7
Разница между единичной матрицей Е и матрицей А
|
Предприятия (виды продукции)
|
Коэффициенты прямых затрат aij
|
Конечный продукт Y
|
|
1
|
2
|
3
|
|
1
|
0,1
|
0,1
|
0,2
|
160
|
|
2
|
0,1
|
0,2
|
0,3
|
180
|
|
3
|
0,1
|
0,2
|
0,3
|
170
|
|
|
|
|
|
|
0,1
|
0,1
|
0,2
|
|
|
A =
|
0,1
|
0,2
|
0,3
|
|
|
0,1
|
0,2
|
0,3
|
|
|
0,8
|
-0,1
|
-0,2
|
|
|
Е-А =
|
0,0
|
0,9
|
-0,2
|
|
|
-0,1
|
0,0
|
0,9
|
|
1.4. Найдем обратную матрицу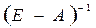 
. Воспользуемся встро-енными функциями MS Excel (математические, обратная матрица) (рис. 5).
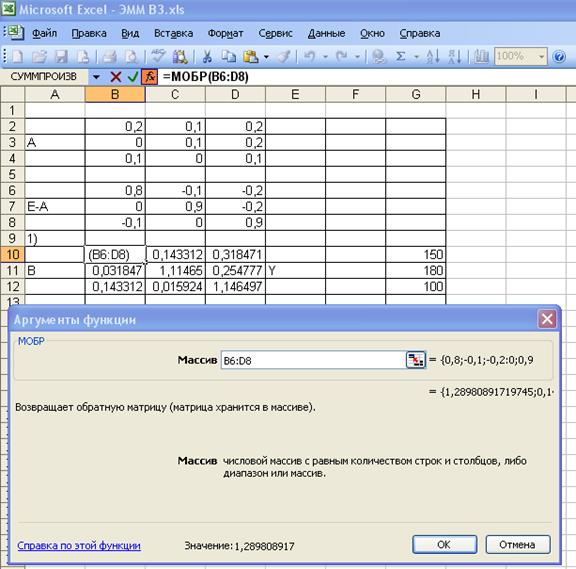
рис. 5 Обратная матрица
1.5. Чтобы определить Валовую
продукцию (матрицу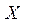
), надо матрицу 
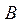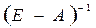= умножить на Конечный
продукт (матрицу 
). Воспользуемся опять встроенными функциями MS Excel (математические, умножение матриц)
(рис. 6).
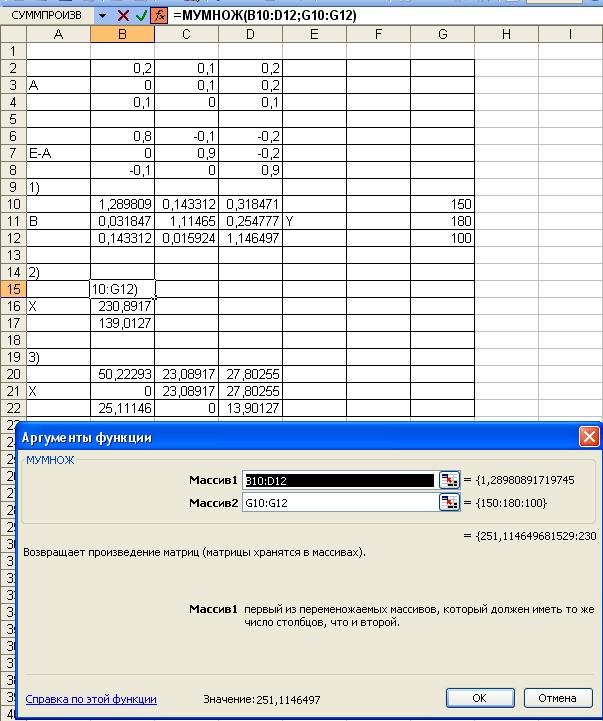
Рис. 6
Определение валовой продукции (матрица Х)
1.6. Матрица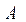 
(матрица коэффициентов прямых материальных затрат)
продуктивна, т.к. существует неотрицательный вектор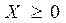 
.
2) Построить баланс (заполнить
таблицу) производства и распределения
продукции предприятий холдинга.
2.1. Межотраслевые поставки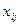 
вычислим по формуле 
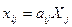(табл. 8)
Таблица 8
|
|
|
|
|
|
50,223
|
23,089
|
27,803
|
|
|
распределение
|
0,000
|
23,089
|
27,803
|
|
|
25,111
|
0,000
|
13,901
|
|
2.2.
Построим баланс производства и распределения продукции предприятий холдинга (таблица
9)
Таблица 9
|
Производящие предприятия
|
Потребляющие предприятия
|
Конечный продукт Y
|
Валовый продукт Х
|
|
|
1
|
2
|
3
|
|
|
|
|
1
|
50,223
|
23,089
|
27,803
|
150
|
251,11
|
|
|
2
|
0
|
23,089
|
27,803
|
180
|
230,89
|
|
|
3
|
25,111
|
0
|
13,901
|
100
|
139,01
|
|
|
Условно чистая продукция
|
175,78
|
184,71
|
69,51
|
430
|
|
|
|
Валовый
продукт
|
251,11
|
230,89
|
139,01
|
|
621,0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условно чистая продукция – это разность между валовым
продуктом и суммой продуктов, которые потребляет каждая отрасль.
Задача 4. 3.
Сгладим ряд с
помощью простой скользящей средней.
Таблица 10
|
t
|
Уt
|
Расчет
|
Выровненный ряд
|
|
1
|
3
|
|
|
|
2
|
7
|
1/3(3 + 7 +10)
|
6,7
|
|
3
|
10
|
1/3(7 + 10 + 11)
|
9,3
|
|
4
|
11
|
1/3(10 + 11 + 15)
|
12,0
|
|
5
|
15
|
1/3(11 + 15 + 17)
|
14,3
|
|
6
|
17
|
1/3(15 + 17 + 21)
|
17,7
|
|
7
|
21
|
1/3(17 + 21 + 25)
|
21,0
|
|
8
|
25
|
1/3(21 + 25 + 23)
|
23,0
|
|
9
|
23
|
|
|
Определим
наличие тренда методом Фостера-Стюарта.
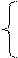K t =
1,
если y1 > yt-1 > ... >y1, 1, если yt < у t-1 <... < y1
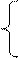0, в остальных случаях 0, в остальных
случаях
S = ∑ St = ∑ (kt + lt);
d = ∑ dt = ∑ (kt – lt). Таблица 11
|
t
|
yt
|
kt
|
lt
|
St
|
dt
|
|
1
|
3
|
-
|
-
|
-
|
-
|
|
2
|
7
|
1
|
0
|
1
|
1
|
|
3
|
10
|
1
|
0
|
1
|
1
|
|
4
|
11
|
1
|
0
|
1
|
1
|
|
5
|
15
|
1
|
0
|
1
|
1
|
|
6
|
17
|
1
|
0
|
1
|
1
|
|
7
|
21
|
1
|
0
|
1
|
1
|
|
8
|
25
|
1
|
0
|
1
|
1
|
|
9
|
23
|
0
|
0
|
0
|
0
|
|
Итого:
|
|
|
|
|
7
|
7
|
С
помощью величины S
проверяется гипотеза о
наличии тенденции в
дисперсиях:
|S - μ| |7 – 3,858|
ts =
─── = ────── =2,44
σ1 1,288
На основе величины d проверяются тенденции в средней:
|d - 0| |7 - 0|
Td = ─── = ──── =3,56
σ2 1,964
По таблице определили значения неизвестных
параметров: μ = 3,858; σ1 = 1,288 ; σ2 = 1,964 .
Проверка осуществляется
на основе критерия Стьюдента:
tKp(a = 0,05; v = п-1 = 9 -1 = 8) = 2,306.
Т. к. 2,44>2,306, то в ряду динамики есть
тенденции в дисперсии. Т.к. 3,56>2,306, то в ряду динамики есть тенденция в
средней.
Построим модель линейную ŷ =аа + a1t
Неизвестные
параметры найдем из системы:
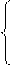a0 * n + a1 *
∑t = ∑y,
a0 *
∑t + a1 * ∑t² = ∑ yt.
∑t 45 ∑y 132 ∑(t – t)(y – y) 162
t = ── =
── = 5, y = ── =
── = 14,67, a1 =
──────── =
─── = 2,7;
n
9 n 9 ∑(t –t)² 60
a0 = y – a1 t = 14,67 - 2,7
* 5 = 1,17. => ŷt = 1,17 + 2
Таблица 12
|
t
|
y1
|
t-t
|
(t – t)²
|
y - y
|
(t
– t)(y - y)
|
ŷt
|
|
1
|
3
|
-4
|
16
|
-11,67
|
46,67
|
3,87
|
|
2
|
7
|
-3
|
9
|
-7,67
|
23,00
|
6,57
|
|
3
j
|
10
|
-2
|
4
|
-4,67
|
9,33
|
9,27
|
|
4
|
11
|
-1
|
1
|
-3,67
|
3,67
|
11,97
|
|
5
|
15
|
0
|
0
|
0, 33
|
0,00
|
14,67
|
|
6
|
17
|
1
|
1
|
2,33
|
2,33
|
17,37
|
|
7
|
21
|
2
|
4
|
6,33
|
12.67
|
20,07
|
|
8
|
25
|
3
|
9
|
10,33
|
31,00
|
22,77
|
|
9
|
23
|
4
|
16
|
8,33
|
33,33
|
25,47
|
|
Итого:
|
45
|
132
|
0
|
60
|
|
162,00
|
132,03
|
Продолжение таблицы 12
|
|
t
|
yt
|
ŷt
|
εt
|
εt ²
|
ТП
|
(εt – εt-1 )²
|
|
1
|
3
|
3,87
|
-0,87
|
0,7569
|
-
|
|
|
2
|
7
|
6,57
|
0,43
|
0,1849
|
0
|
1,69
|
|
3
|
10
|
9,27
|
0,73
|
0,5329
|
1
|
0,09
|
|
4
|
11
|
11,97
|
-0,97
|
0,9409
|
1
|
2,89
|
|
5
|
15
|
14.67
|
0,33
|
0,1089
|
1
|
1,69
|
|
6
|
17
|
17,37
|
-0,37
|
0,1369
|
1
|
0,49
|
|
7
|
21
|
20,07
|
0,93
|
0,8649
|
0
|
1,69
|
|
8
|
25
|
22,77
|
2,23
|
4,9729
|
1
|
1,69
|
|
9
|
23
|
25,47
|
-2,47
|
6,1009
|
-
|
22,09
|
|
Итого:
|
45
|
132
|
132,03
|
-0,03
|
14,6001
|
5
|
32,32
|
Продолжение таблицы 12
|
εt
─
yt
|
εt • εt - 1
|
|
0, 2900
|
|
|
0,0 614
|
- 0, 3741
|
|
0, 0730
|
0, 3139
|
|
0, 0882
|
- 0,7081
|
|
0, 0220
|
- 0, 3201
|
|
0, 0218
|
- 0, 1221
|
|
0, 0443
|
- 0, 3441
|
|
0, 0892
|
2, 0739
|
|
0, 1074
|
- 5, 5081
|
|
Итого:
|
0,7973
|
- 4,9888
|
Оценим
адекватность построенной модели.
а) Проверку
случайности уровней остаточной компоненты проверим на основе критерия
поворотных точек.
Общее число поворотных точек равно 5.
Критерий
случайности отклонений от тренда при уровне вероятности 0,95 можно представить
так:
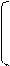
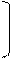2(n – 2) 16n - 29
p>────
–- 1,96√─────
3 90
( р - количество поворотных точек в случайном
ряду, 1,96 – квант нормального
распределения для 5%-го уровня значимости).
2(9 – 2) 16*9 – 29
q = ───── - 1,96 √────── =
2,45 =
2.
3 90
б) Проверку
отсутствия автокорреляции проведем двумя методами: по d-критерию
Дарбина-Уотсона (d1 = 1,08 ; d2 = 1,36) и по
первому коэффициенту автокорреляции r(1) = 0,36.
n
∑ (εt – εt-1)²
t=2 32,3200
d=
───── =
───── = 2,21
n 14,6001
∑ε t ²
t=1
Т.к. d >2, то имеет место отрицательная автокорреляция. Поэтому находим d´ = 4 — 2,21 = 1,79.
Т.к. 1,36 < 1,79
< 2, то ряд остатков не коррелирован.
n
∑εt εt-1 -4,9888
t=2
r(1)=──────
= ───── =
- 0,34.
n 14,6001
∑εt²
t=1
Т.к. |- 0,34| < 0,36, то уровни ряда
остатков независимы.
в) Проверка соответствия ряда остатков нормальному
распределению определяем по RS-критерию.
ε max - ε min
RS = ─────; εmax = 2,23; εmin = - 2,47;
Sε
2,23 + 2,47
RS = ─────── = 3,48.
1,3509
Т. к. 2,7 < 3,48
< 3,7, то уровни ряда остатков подчиняются нормальному распределению.
Таким образом,
можно говорить об удовлетворительном качестве модели и возможности проведения прогноза показателя y(t) на 2 шага вперед.
Строим точечный
и интервальный прогноз на 2 шага вперед.
ŷ10
=1,17 + 2,7*10 = 28,17; ŷ11 =1,17 + 2,7*11
= 30,87.
Для построения интервального прогноза рассчитаем
доверительный интервал. Примем значение уровня значимости α = 0,3, следовательно,
доверительная вероятность равна 70%, а критерий Стьюдента при v = m - 2 = 9 - 2 = 7 равен tα =1,12.
Таблица 13
|
Шаг
|
Прогноз
|
Верхняя
граница
|
Нижняя граница
|
|
1
|
28,17
|
25,28
|
31,05
|
|
2
|
30,87
|
27,81
|
33,92
|
Модель Брауна
Yp (t) = а0 (t -1) + а1(t -1) * к, где к - количество шагов прогнозирования.
a1(t) = а1 (t -1) + а2 * E(t), E(t)
= Y(t0 - Yp(t),
а0(t) = a0 (t -1) + а1 (t - 1) + (1 - β2) *E(t).
Начальные оценки параметров получим по
первым пяти точкам при помощи
метода наименьших квадратов:
Таблица 14
|
t
|
Y(t)
|
t²
|
Y(t)*t
|
|
1
|
3
|
1
|
3
|
|
2
|
7
|
4
|
14
|
|
3
|
10
|
9
|
30
|
|
4
|
11
|
16
|
44
|
|
5
|
15
|
25
|
75
|
|
Итого:
|
15
|
46
|
55
|
166
|
|
Среднее значение:
|
3
|
9,2
|
11
|
33,2
|
a1(0) =2,8; a0(0) = 9,2 – 2,8 * 3 = 0,8.
При α = 0,4; k = 1; β =1 – 0,4 = 0,6. Получим:
Таблица 15
|
t
|
Y(t)
|
a0(t)
|
a1(t)
|
Yp(t)
|
E(t)
|
E²(t)
|
ТП
|
(E(t)-E(t-1))2
|
|
E(t)/Y(t)
щ
|
|
|
|
0,80
|
2.80
|
|
|
|
-
|
-
|
-
|
|
1
|
3
|
3,50
|
2,70
|
3,60
|
-0,60
|
0,36
|
-
|
-
|
0,20
|
|
2
|
7
|
6,33
|
2,83
|
6,21
|
0,79
|
0,63
|
1
|
1,938
|
0,11
|
|
3
|
10
|
9,30
|
2,96
|
9,17
|
0,83
|
0,70
|
0
|
0,002
|
0,08
|
|
4
|
11
|
12,06
|
2,76
|
12,26
|
-1,26
|
1,60
|
1
|
4,401
|
0,11
|
|
5
|
15
|
14,85
|
2,79
|
14,82
|
0,18
|
0,03
|
1
|
2,074
|
0,01
|
|
6
|
17
|
17,54
|
2,69
|
17,64
|
-0,64
|
0,41
|
1
|
0,670
|
0,04
|
|
7
|
21
|
20,35
|
2,81
|
20,23
|
0,77
|
0,60
|
0
|
2,002
|
0,04
|
|
8
|
25
|
23,46
|
3,11
|
23,16
|
1,84
|
3,38
|
1
|
1,134
|
0,07
|
|
9
|
23
|
25,99
|
2,54
|
26,56
|
-3,56
|
12,68
|
-
|
29,155
|
0,15
|
|
Итого:
|
|
|
|
|
|
20,38
|
5
|
41,375
|
0,83
|
При α = 0,7; k = 1, β = 1 - 0,7 = 0,3
получаем: Таблица 16
|
t
|
Y(t)
|
a0(t)
|
a1(t)
|
Yp (t)
|
E{t)
|
E2(t)
|
ТП
|
(E(t)-E(t -1))2
|
│E(t)/Y(t)│
|
|
|
0,80
|
2,80
|
|
|
|
-
|
-
|
|
|
1
|
3
|
3,31
|
2,51
|
3,60
|
-0,60
|
0,36
|
-
|
-
|
0,20
|
|
2
|
7
|
6,39
|
3,09
|
5,81
|
1,19
|
1,41
|
1
|
1,105
|
0,17
|
|
3
|
10
|
9,74
|
3,34
|
9,48
|
0,52
|
0,27
|
0
|
1,307
|
0,05
|
|
4
|
11
|
12,06
|
2,32
|
13,08
|
-2,08
|
4,32
|
1
|
16,395
|
0,19
|
|
5
|
15
|
14,69
|
2,63
|
14,38
|
0,62
|
0,38
|
1
|
15,499
|
0,04
|
|
6
|
17
|
17,16
|
2,47
|
17,31
|
-0,31
|
0,10
|
1
|
0,080
|
0,02
|
|
7
|
21
|
20,30
|
3,14
|
19,63
|
1,37
|
1,87
|
1
|
3,148
|
0,07
|
|
8
|
25
|
24,21
|
3,91
|
23,45
|
1,55
|
2,42
|
0
|
0,296
|
0,06
|
|
9
|
23
|
25,61
|
1,40
|
28,11
|
-5,11
|
26,14
|
-
|
562,747
|
0,22
|
|
Итого:
|
|
|
|
|
|
37,26
|
5
|
600,577
|
1,02
|
Лучшее значение
параметра сглаживания α = 0,4, так как меньше Eотн
Eотн = 0,83/9• 100% = 9%
при α = 0,4
Eотн = 1,02/9• 100% = 11% при α = 0,7.
Оценим
адекватность модели Брауна с параметром сглаживания α = 0,4
а)
2 ( 9 – 2) 16*9 - 29
────── - 1,96√ ─────── = 2,45 = 2.
3 90
Т.к. 5>2,
то проверка случайности
ряда остатков по критерию пиков дает положительный результат.
б) d1 = 1,08 ; d2 = 1,36 ;
41,37
d = ───── = 2,03.
20,38
Т. к. 1,08<2,03, то с вероятностью
95% гипотеза об отсутствии автокорреляции остатков принимается
R E max – E min 20,38
в) ─ =
────── ;
S v = √ ───── = 1,60.
S S v
8
R 1, 84 + 3,56
─ =
──────── = 3, 38.
S 1, 60
Т.к. 3,38 принадлежит 2, 7; 3, 7 гипотеза о нормальном распределении ряда
остатков верна.
Построим прогнозные значения для модели
Брауна с параметром α=0,4.:
Yp
(10) = 25,99+2,54=28,53;
Yp (11) = 25,59+2,54 * 2 = 31,06.
u(1)
= 4,03; u(2) = 4,26.
Таблица 17
|
Прогноз
|
Нижняя граница
|
Верхняя граница
|
|
28,53
|
24,50
|
32,56
|
|
31,06
|
26,80
|
35,33
|
График для линейной модели
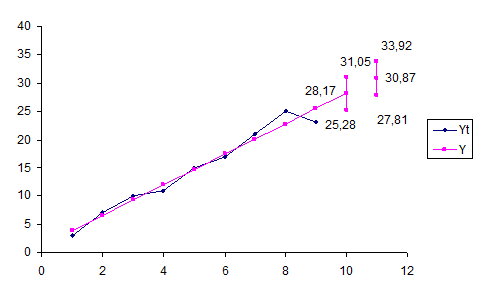
Рис.7. График для линейной модели
График для модели Брауна с
параметром сглаживания α=0,4
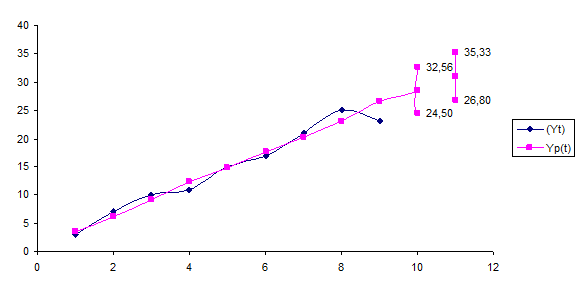
Рис.8. График для модели Брауна с параметром
сглаживания α=0,4
Литература
1. Орлова И.В. Экономико-математические
методы и модели. Выполнение расчетов в среде Excel. Практикум. - М.: Финстатинформ,
2000.
2. Орлова И.В. Экономико-математическое
моделирование. Практическое пособие по решению задач - М.: ВЗФЭИ. Вузовский
учебник, 2004.
3. Федосеев В.В., Гармаш А.Н., Орлова
И.В., Половников В.А. Экономико-математические методы и прикладные модели. 2-е
изд. – М.: ЮНИТИ-ДАНА, 1999.
4. Гармаш А.Н.,Концевая Н.В., Орлова
И.В., Экономико-математические методы и прикладные модели. Задания для
выполнения контрольной и лабораторной работ. - М.: ВЗФЭИ, 2006.