четным данным за прошлый квартал предприятие имело коэф­фициент рентабельности производства  p и коэффициент пере­менных затрат  r.

В результате такого планово-управленческого решения инди­кативный прогноз прибыли предприятия составляет I. А это зна­чит, что если все запланированные параметры будут выдержаны в процессе практической реализации плана, то предприятие полу­чит ту самую прибыль, которую оно себе запрограммировало.

Однако реальная экономическая жизнь и хозяйственная ры­ночная ситуация могут существенно изменить запланированные параметры, в частности изменить объем производства и реали­зации продукции. Предположим, что объем производства соста­вит уровень, при котором наступает граница абсолютной без­убыточности производства. Определим этот уровень как b₀

Формула 4.9 дает возможность установить, от чего и в каком размере объема реализации наступает искомая граница.

Тогда величина страхового коэффициента составит:

где b — объем реализации продукции плану (может быть од­нозначно определен из формулы 4.6 и заменен равным ему вы­ражением);

b₀ — объем реализации продукции, при котором наступает граница абсолютной безубыточности производства, определяемый по формуле 4.9.

Произведя соответствующие преобразования полученного выражения, получим значение страхового коэффициента абсо­лютной безубыточности по объему реализации продукции:

                         (4.13)

По аналогии определим величину коэффициента относи­тельной безубыточности с использованием формул 4.6 и 4.12:

где b₁ — объем реализации продукции, при котором наступа­ет граница относительной безубыточности производства.

После преобразований получим:

                  (4.14)

                        

Зададим конкретные числа и произведем расчет страховых коэффициентов по объему реализации продукции.

Пусть предприятие в базовом периоде имело  p = 1,15 и r = 0,5.

Для анализируемого периода предприятие планирует обеспе­чить объем реализации продукции b = 1,2, затраты на уровне g = 0,98 и цену реализации d = 1,05. Условно-постоянные затра­ты не меняются (т.е. f = 0). Определим страховые коэффициен­ты для принятого планово-управленческого решения.

По формуле 4.13 рассчитаем страховой коэффициент абсо­лютной безубыточности производства:

По формуле 4.14 исчислим страховой коэффициент относи­тельной безубыточности производства:

Полученный результат свидетельствует о тех запасах прочно­сти, которыми обладает плановая величина объема реализации продукции. Так, можно констатировать, что предприятие будет работать с прибылью, если объем реализации продукции в силу ряда внешних и внутренних причин не снизится против заплани­рованной величины больше чем на 74,6% и превысит b₀ = 0,687 (1,2 : 1,746 = 0,687).

Можно также утверждать, что предприятие получит прибыль не ниже чем в базовом периоде, если объем реализации продук­ции снизится по сравнению с планом не больше, чем на 34,3% и превысит b₁= 0,893 (1,2 : 1,343 = 0,893).

Таким образом, страховые коэффициенты опосредованно сигнализируют предприятию, насколько надежно принятое пла­ново-управленческое решение, какими запасами прочности оно обладает, какова вероятность того, что неопределенность ры­ночной ситуации может вывести предприятие из состояния ус­тойчивости, стабильности, прибыльности работы. И чем выше эти коэффициенты, тем надежнее предприятие будет чувство­вать себя в рынке.

Проанализируем полученные зависимости (формулы 4.13 и 4.14) с точки зрения количественных значений страховых коэффи­циентов и установления закономерности их изменения. Прежде всего, отметим, что с увеличением планируемого объема реализации продукции, цен реализации и снижение плановой величины затрат (параметры будут технически, экономически и производст­венно обоснованы) значения страховых коэффициентов будут рас­ти. Это вытекает из того, что все перечисленные параметры нахо­дятся в числителе формул по определению искомых коэффициен­тов. Интерес поэтому представляет анализ величины страховых ко­эффициентов в зависимости от исходных параметров p и r.

Посмотрим, что будет происходить с величиной страховых коэффициентов, если изменять параметр r. Вначале проведем анализ по конкретным цифровым данным на основе значений параметров рассмотренного выше примера (т.е. для  b = 1,2; d = 1,05; g = 0,98; p = 1,15;  f =0). Результаты расчетов для разных значений парамет­ра r приведены в табл. 4.5.

Приведенные цифры говорят о том, что для условий рассмат­риваемого примера страховые коэффициенты по мере увеличения доли переменных затрат в себестоимости продукции неукосни­тельно возрастают. А как будет для других исходных условий производства? Не изменится ли найденная закономерность?

Возьмем формулу 4.13 и проанализируем ее, предварительно несколько видоизменив:

Таблица 4.5

Закономерность изменения величины страховых коэффициентов в зависимости от коэффициента переменных затрат

Исходные данные	Значение коэффициента  r	Величина страховых коэффициентов
абсолютной безубыточности	относительной безубыточности
b = 1,2	0,1	1,503	1,288
d = 1,05	0,3	1,59	1,309
g = 0,98	0,5	1,746	1,343
p = 1,15	0,7	2,11	1,407
f  = 0,0	0,9	3,93	1,572

Из полученного выражения однозначно следует, что чем больше коэффициент r, тем меньше знаменатель первого сла­гаемого и, следовательно, больше величина страхового коэффи­циента абсолютной безубыточности производства (ибо второе слагаемое остается постоянным). Аналогичный результат можно получить при анализе величины страхового коэффициента отно­сительной безубыточности производства с той лишь разницей, что изменения искомых коэффициентов носят не столь выраженный характер.

Что касается коэффициента рентабельности p, то, как следует из формулы 4.12, его увеличение будет повышать значение стра­хового коэффициента абсолютной безубыточности. И это вполне понятно, ибо, если предприятие в базовом периоде сработало с высокой эффективностью, то тем самым оно заложило более вы­сокий уровень стабильной и безубыточной работы в будущем.

Проведя соответствующие преобразования модели типа 4.6, можно получить формулы для определения страховых коэффи­циентов абсолютной и относительной безубыточности по цене и по себестоимости:

                                    (4.15)

      

                                   (4.16)

 

              

                                 (4.17)

                         (4.18)

где и — страховые коэффициенты абсолютной и относительной безубыточности по цене;

  и   — страховые   коэффициенты  абсолютной  и относительной безубыточности по себестоимости.

Учитывая важность и высокую информационную значимость страховых коэффициентов, опосредованно и косвенно устра­няющих неопределенность рыночной ситуации, а также способ­ность выполнения ими функции определения запасов прочно­сти планово-управленческого решения и вероятности безубы­точности работы предприятия, можно рекомендовать ввести эти коэффициенты в практику бизнес―  планирования производства.

4.6. Компенсационные соотношения

       прибылеобразующих параметров

Принимая различные варианты планово-управленческих ре­шений, очень часто варьируют отдельными прибылеобразующими параметрами. Однако весьма полезно оперировать двумя параметрами-антиподами одновременно. Здесь имеются в виду такие пары, как «цена реализации — объем реализации», а так­же «затраты на производство — цена реализации». Нетрудно по­нять, что эти пары взаимосвязаны не только чисто физически в одной математической модели, но и экономически.

Поэтому крайне важно знать, как изменение одного парамет­ра из выделенной пары может быть компенсировано изменением другого параметра, но так, чтобы прибыль осталась на уровне ба­зового периода. Познания в этой области могут быть полезны для быстрой оценки выгодности того или иного решения в условиях меняющейся конъюнктуры рынка как в области приобретения средств производства для своего бизнеса, так и в сфере реализа­ции изготовленной продукции. Рассмотрение этого вопроса про­ведем на примере пары параметров «цена — объем реализации».

Хорошо известно, что в условиях рыночных отношений дей­ствует непреложный закон: больше цена товара — меньше ско­рость его реализации, а следовательно, в определенную единицу времени должен быть сокращен объем производства данного то­вара с целью полной его реализации потребителю. Справедливо и обратное действие: меньше цена товара — больше скорость его реализации, увеличивается спрос на этот товар и, чтобы его удовлетворить, надо больше производить товарной продукции.

Разумеется, снижение цены на товар приводит к сокраще­нию получаемой прибыли и, чтобы эту потерю компенсировать, необходимо увеличить объем производства и реализации про­дукции. В этом случае как раз и возникает вопрос: насколько нужно его увеличить, каково компенсационное соотношение между сокращением одного параметра (цены реализации) и воз­растанием другого (объема реализации)?

Для ответа на этот вопрос воспользуемся основной формулой индекса прибыли 4.6 для определения компенсационного соот­ношения между двумя параметрами, имея в виду, что цену реали­зации понизим на величину ∆d, а индекс прибыли примем I = 1 . Дополнительно примем g = 1 и  f = 0. Тогда, после подстановки всех исходных данных в указанную формулу и простейших алгеб­раических преобразований, получим:

                                              (4.19)

где ∆b — необходимый прирост объема реализации с целью компенсации потерь прибыли при снижении цены реализации на ∆d.

Как видно из формулы, компенсационное соотношение меж­ду двумя параметрами зависит от коэффициента рентабельности производства в базовом периоде и коэффициента переменных за­трат. На конкретном примере рассмотрим, как они действуют и влияют на искомое соотношение. Пусть p = 1,235 и r = 0,58. Оп­ределим прирост объема реализации продукции, компенсирую­щий потерю прибыли, если планируется снизить цену товара на ∆d = 0,03 (т.е. на 3%). Подставим эти данные в формулу 4.19:

Полученный результат трактуется следующим образом. При фиксированных исходных данных снижение цены товара на 3% компенсируется при формировании той же прибыли приростом объема производства и реализации продукции почти на 6%. Ес­ли этот прирост будет больше, то прибыль, несмотря на сниже­ние цены реализации на 3%, будет прирастать, т.е. станет боль­ше, чем была в базовом периоде.

Проведенные расчеты по формуле 4.19 дали результаты, ко­торые приведены в табл. 4.6.

Таблица 4.6

Компенсационный прирост объема реализации продукции в процентах при снижении цены товара на один процент

 

Коэффициент переменных затрат, r	Коэффициент рентабельности производства,  p
1,05	1,15	1,25	1,5	1,75	2
0,1	1,105	1,109	1,09	1,07	1,061	1,053
0,2	1,235	1,21	1,19	1,154	1,129	1,111
0,3	1,4	1,353	1,316	1,25	1,207	1,176
0,4	1,615	1,533	1,47	1,363	1,296	1,25
0,5	1,91	1,77	1,666	1,5	1,4	1,333
0,7	3	2,555	2,27	1,875	1,666	1,538
0,8	4,2	3,285	2,777	2,143	1,842	1,666
0,9	7	4,6	3,57	2,5	2,06	1,82

Как видно из табл. 4.6, компенсационная величина прироста объема реализации продукции снижается с увеличением коэффи­циента рентабельности и растет с увеличением коэффициента переменных затрат. Видно также, что количество процентов при­роста объема реализации для компенсации потерь прибыли все­гда больше единицы: незначительно больше — при небольших коэффициентах переменных затрат порядка r = 0,1 r ¸ 0,2, сущест­венно больше, когда r > 0,7. При промежуточных значениях этого коэффициента компенсационный прирост объема реализации продукции составляет от 1,3 до 2,5%. И очень часто такой прирост объема производства и реализации не только для компенса­ции потерь прибыли, но и для ее наращивания, является оправ­данным. Это связано с одним из возможных стратегических на­правлений получения прибыли, когда снижаются цены на реали­зуемый товар, но существенно увеличивается скорость его прода­жи, растет товарооборот, а следовательно увеличивается объем производства продукции для поддержания на определенном уровне насыщенности рынка товарами в соответствии со склады­вающимся спросом. Такая стратегия способна не только воспроизвести прибыль на прежнем уровне, но и многократно его превысить. И та фирма, которая это поняла и применяет в своей деятельности, имеет, как правило, успех, выходит победителем в конкурентной борьбе с многочисленными производителями ана­логичных и взаимозаменяемых товаров.

4.7. Учет производственной мощности предприятия при       прогнозировании прибыли

Богатый мировой и отечественный опыт свидетельствует, что практически ни одно производство не остается таким, каким оно создано изначально. Каждое из них с течением времени постоян­но находится в движении и развитии, совершенствуется и техни­чески, и организационно. Для этого существуют многочисленные формы и методы: рационализация и модернизация, техническое перевооружение и реконструкция предприятия, переоснащение производства и его простое расширение.

Выбор того или иного направления развития предприятия за­висит от многих факторов, вся совокупность которых учитывает­ся в процессе принятия решения и обусловлена теми конкретны­ми задачами, которые стоят в стратегическом и тактическом пла­нах предприятия. Тем не менее, независимо от того, какое на­правление будет взято фирмой на вооружение, реализация лю­бого из них потребует дополнительных прямых переменных и ус­ловно-постоянных затрат. Поэтому развитие и расширение про­изводства продукции обязательно должно найти отражение в параметрической модели формирования прибыли: для переменных затрат — в виде изменения себестоимости продукции, для услов­но-постоянных затрат — их прирост и изменение. Причем для модели типа 4.6 эти изменения отражаются в параметрах g и f.

Если изменение себестоимости продукции под влиянием прямых переменных затрат можно учесть прямым расчетом, то изменение условно-постоянных затрат заслуживает особого раз­говора. Дело в том, что дополнительные условно-постоянные затраты в связи с развитием производства направляются на содер­жание и эксплуатацию вновь введенных производственных фон­дов и мощностей, на заработную плату дополнительного кон­тингента инженерно-технического и управленческого персонала, дополнительных вспомогательных рабочих и т.п.

Однако изменение условно-постоянных затрат обязательно должно сопровождаться в расчетах прибыли изменением объема производства и реализации продукции. Следует иметь в виду, что последний параметр может рассматриваться как величина потенциальная (тогда он будет отражать производственную мощность предприятия) и как величина фактическая (тогда его величина конкретно и однозначно будет характеризовать плани­руемый объем производства продукции).

Следовательно, в информационном плане разными проектами должны быть заданы диапазоны потенциального изменения ко­эффициента b и соответствующего ему коэффициента f. После этого можно произвести расчет индекса прибыли по формуле 4.6.

Информацию о значениях указанных показателей рекомен­дуется задавать следующим образом:

Максимальная величина

коэффициента            b           b₀           b₁           b₂

коэффициента           f             f₀                   f₁                 f₂

 

Истолкуем, например, такую заданную информацию:

       

b₀ = 1,15                 b₁ = 1,46               b₂  = 1,92

f₀ = 0,0                   f₁ = 0,21                 f₂ = 0,37

 

Возьмем цифры первого столбца. В них много полезной ин­формации. Во-первых, становится ясно, что можно увеличить объем производства и реализации продукции по сравнению с базовым периодом максимум на 15%, и при этом никаких до­полнительных постоянных затрат не потребуется. Во-вторых, в базовом периоде производственная мощность предприятия недоиспользовалась (примерно на 15%). Поэтому, в-третьих, фак­тический выпуск продукции может принимать любое значение, например 1,02; 1,07; 1,12 или 1,15 (но не выше).

 Цифры второго столбца говорят о том, что, согласно проек­ту, можно расширить выпуск продукции максимум на 46%, но при этом условно-постоянные затраты, опять-таки согласно проекту, возрастут на 21% (f = 0,21) по сравнению с базовым периодом. Фактический объем производства в данном случае может принимать любое значение между b = 1,15 и  b = 1,46.

Аналогичным образом трактуются цифры третьего столбца. Они отражают показатели альтернативного варианта проекта, в котором можно расширить производство продукции максимум на 92%, увеличив при этом условно-постоянные затраты на 37% по сравнению с базовым периодом.

Таким образом, весь массив предложенной экономической информации по развитию производства представляет собой сравнение трех различных вариантов. Первый вариант отражает существующее положение и возможность увеличения объема производства, второй и третий варианты — это сравниваемые альтернативные проектные решения, из которых нужно ото­брать наиболее приемлемое.

Рассмотрим конкретный расчетный пример для вышеприве­денных исходных данных. Дополнительно примем:

p = 1,2;     d = 1,03; g = 0,98;   r = 0,5.

Определим индекс прибыли для значений объема производ­ства и реализации продукции:

b = 1,08;  b = 1,15;  b = 1,46; b = 1,92.

         Для b = 1,08

 

        Для b = 1,15 (первый вариант)

Для b = 1,15 (второй вариант)

  Для b = 1,46  (второй вариант)

Для b = 1,46 (третий вариант)

    

Для b = 1,92 (третий вариант)

Полученная информация может быть проиллюстрирована с помощью графика (рис.4.2), где представлены три кривые, харак­теризующие три проектных варианта развития предприятия и их потенциалы в виде производственных мощностей и индекса при­были. Последние могут быть получены при соответствующих объемах производства и уровне использования производственной мощности предприятия по каждому конкретному решению.

Рис.4.2. Влияние производственной мощности на индекс прибыли

Оценив полученную информацию с учетом перспектив спроса на выпускаемую продукцию предприятие может выбрать тот вари­ант развития, который ему представится выгодным и наиболее перспективным. Так, если предприятие решит оставить все без изменений, то прибыль можно максимально увеличить на 84,7%. Ес­ли оно решит развиваться по второму варианту, то прибыль может возрасти максимум на 149,4%. Третий вариант развития несет в се­бе перспективы увеличения прибыли максимально на 283,3%.

4.8. Оценка влияния прибылеобразующих параметров на конечный результат

Как было установлено, используя параметрическую модель, можно определить, как изменится прибыль предприятия при со­блюдении запланированных параметров в анализируемом периоде. Однако очень часто возникает потребность в информации о том, каков вклад каждого прибылеобразующего параметра в конечном результате производства. Иначе говоря, желательно из общего ре­зультата вычленить влияние на величину создаваемой прибыли каждого из действующих параметров. Эту задачу с использованием параметрической модели, например типа 4.6, можно решить с по­мощью аналитического метода цепных подстановок.

Рассмотрим этот метод на конкретном примере из предыду­щего параграфа для второго варианта развития предприятия. Исходные данные следующие: p — 1,2; r = 0,5; d =1,03; g = 0,98; f = 0,21. Причем коэффициент изменения объема производства b = 1,34 (т.е. в пределах между 1,15 и 1,46).

Результаты расчетов индекса прибыли методом цепных под­становок представлены в табл.4.7.

Таблица 4.7

Влияние  прибылеобразующих параметров

 на конечный результат

 

№ п/п	Прибылеобразующие параметры	Индекс прибыли I	Влияние параметра, %
d	g	b	F
1	2	3	4	5	6	7
0	1	1	1	0	1	0
1	1,03	1	1	0	1,18	18
2	1,03	0,98	1	0	1,28	8,47
3	1,03	0,98	1,34	0	2,565	100,4
4	1,03	0,98	1,34	0,21	2,04	− 20,5

Зафиксированные в таблице результаты были рассчитаны по каждой строчке таблицы путем подстановки значений парамет­ров в модель типа 4.6. Покажем такой расчет, например, для строки 2. Для нее характерно изменение цены товара (d = 1,03) и снижение себестоимости продукции (g — 0,98). Остальные два параметра приняты без изменений (b =1; f = 0). Подставим данную информацию в формулу 4.6 и получим:

Этот результат зафиксирован во второй строке шестой графы таблицы.

Рассмотрим, как получаются цифры в строках таблицы и как надо истолковывать результаты расчетов в графах 6 и 7.

В нулевой строке все прибылеобразующие параметры приня­ты на уровне базового периода, т.е. без изменений. Следователь­но, индекс прибыли будет равен единице и влияние параметра на прибыль составит ноль процентов.

В первой строке принимаем изменение цены товара d = 1,03. Остальные параметры принимаем без изменений. По формуле 4.6 определяем индекс прибыли. Он будет равен I = 1,18. Это значит, что прирост цены на 3% увеличит прибыль на 18%.

Определяется влияние параметра по формуле

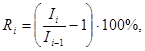                   (4.20)

где R_i  — влияние выделенного параметра для i-ой строки таблицы;

I_i, I_i-1 — индексы прибыли соответственно для  i-ой  и предшествующей ей строки.

Для второй строки принимаем ранее установленное увеличе­ние цены на 3% и снижение себестоимости на 2%. В результате получим совокупное влияние на индекс прибыли двух изменен­ных параметров. Это влияние повышает индекс прибыли до 1,28. Влияние цены на индекс прибыли составляет 1,18. Следо­вательно, прирост от 1,18 до 1,28 характеризует влияние сниже­ния себестоимости продукции. Оно составляет 8,47%.

Рассуждая аналогичным образом и производя каждый раз вычисления индекса прибыли для всех последующих строк, можно установить влияние каждого параметра на конечную ве­личину прибыли. Так, в третьей строке выясняется влияние на прибыль увеличения объема производства продукции (оно составляет 100,4%), а в четвертой строке — влияние увеличения условно-постоянных затрат, снижающее прибыль на 20,5%.

Окончательный итог, учитывающий совокупное действие всех прибылеобразующих параметров, приводит к увеличению индекса прибыли в 2,04 раза.

Такова методика оценки влияния каждого параметра на ко­нечный результат деятельности предприятия.

4.9. Структурные сдвиги в производстве продукции

             и их влияние на прибыль предприятия

Очень часто на предприятиях происходит снятие с производ­ства устаревших и малоперспективных видов продукции и ос­воение новых, прогрессивных и перспективных моделей, типов и видов продукции. Иначе говоря, происходят структурные сдвиги. Они существенным образом влияют на прибыль пред­приятия. Столь важные изменения нуждаются в специальных исследованиях, ибо они имеют чрезвычайно большое значение не только для теории, но особенно для практики.

В принципе возможны следующие варианты структурных сдвигов во времени (рис. 4.3):

первый вариант — n  (при т = 0; L = 0);

второй вариант — n + т (L = 0);

третий вариант — n + L (т = 0);

четвертый вариант — т + L (n = 0);

пятый вариант — n + т + L.

Для всех этих вариантов экономический смысл n, т, L пред­ставлен в разделе 4.1. Здесь же напомним, что все параметры отражают соответственно количество снимаемых с производст­ва, оставляемых в производстве и осваиваемых в производстве позиций продукции.

                                        m                         n                           L

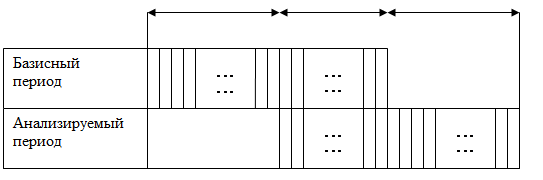Рис. 4.3. Возможные варианты совпадения позиций

выпускае­мой продукции в базисном и анализируемых периодах

 

Кроме данных о выпускаемых видах продукции в обоих пе­риодах необходимо иметь информацию об их объемах, ценах и себестоимости производства в таком виде, как это представлено в табл. 4.8 (где т + n + L = 7).

Таблица 4.8

Необходимая информация о выпускаемой продукции и характере структурных сдвигов

 

Период	Показатели	Позиция выпускаемой продукции
1	2	3	4	5	6	7
Базовый	объем производства	Nd1	Nd2	Nd3	Nd4	0	0	0
цена	Цd1	Цd2	Цd3	Цd4	Ца5	Ца6	Ца7
себестоимость	Сd1	Сd2	Сd3	Сd4	Са5	Са6	Са7
Анализируемый	объем производства	0	0	Nа3	Nа4	Nа5	Nа6	Nа7
цена	Цd1	Цd2	Ца3	Ца4	Ца5	Ца6	Ца7
себестоимость	Сd1	Сd2	Са3	Са4	Са5	Са6	Са7
Примечание: здесь т = 2;  n = 2;  L = 3.

Расчеты индекса прибыли при структурных сдвигах следует производить по тем же параметрическим моделям типа 4.5 или 4.6 с небольшой разницей, учитывающей эту характерную осо­бенность производства. Модификации этих моделей выгладят следующим образом:

                 (4.21)

                                 (4.22)

где p_с — коэффициент рентабельности производства, учиты­вающий структурные сдвиги.

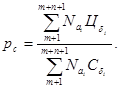                (4.23)

Все представленные в формуле 4.23 параметры имеют тот же экономический смысл, что и в формулах 4.2 и 4.3, но взяты по конкретным позициям продукции.

После подготовки всей необходимой информации считыва­ется индекс прибыли, по которому можно судить, насколько удачным оказались проведенные структурные сдвиги. Очень часто при этом результаты расчета отличаются от ожидаемых и порой   выглядят  парадоксальными.   Вот   конкретный   пример. Пусть предприятие в базовом периоде выпускало и предполагает выпускать в анализируемом  периоде три  вида  сопоставимой продукции (т.е. n = 3 при т = 0 и L = 0). Коэффициент переменных затрат r  = 0,3. Остальные исходные данные по видам продукции представлены ниже.

Базовый период	Объем производства, тыс. шт.	80	250	100
Цена реализации, руб./шт.	6,3	8,7	10,4
Себестоимость, руб./шт.	5,1	7,2	12,5
Анализируемый период	Объем производства, тыс. шт.	80	250	х
Цена реализации, руб./шт.	6,3	8,7	10,4
Себестоимость, руб./шт.	5,1	7,2	12,5

Из приведенных данных видно, что первые два вида продук­ции рентабельны, их производство и реализация приносят пред­приятию прибыль (так как цена превышает себестоимость). Иначе обстоит дело с третьим видом продукции. Она убыточна. Производство и реализация каждой единицы такой продукции приносят предприятию убыток в размере 2,1 руб./шт., ибо цена ее реализации ниже себестоимости.

Возникает вопрос: как поступить предприятию, чтобы повы­сить прибыльность производства? Сокращать ли производство убыточной продукции или, наоборот, увеличивать его? Именно поэтому в строке «объем производства» для анализируемого пе­риода среди исходных данных примера стоит неизвестная вели­чина  x.

Чтобы разрешить этот вопрос, обратимся к параметрической модифицированной модели. Проведенные расчеты дали сле­дующие результаты:

Объем производства убыточ­ной продукции x, тыс. шт.	0	25	50	75	100	125	150
Индекс прибыли	− 1,54	−0,91	−0,27	0,36	1,0	1,64	2,27

 

Из приведенных данных видно, что с увеличением произ­водства убыточной продукции при фиксированных для этого примера исходных данных индекс прибыли возрастает.

Если  в  базовом  периоде  предприятие  получило  прибыль  в  размере

80000 (6,3−5,1) + 250000 (8,7 − 7,2) + 100000(10,4 − 12,5) = 261000 руб., то, изменив объем производства и реализации третьего вида продукции, прибыль составит:

при x =  0 →   (−1,54) · 261000 =  − 401940 руб.;

приx =  50 →  (− 0,27) · 261000 = −  70470 руб.;

при x =  75 →  0,36 · 261000 = 93960 руб.;

при x = 100 → 1 · 261000 = 261000 руб.;

при x = 125 → 1,64 · 261000 = 428040 руб.;

при x = 150 →  2,27 · 261000 = 592470 руб.

Как видно из расчетов, если вообще снять с производства убы­точную продукцию, то предприятие понесет от всей своей дея­тельности убыток в размере примерно 402 тыс. руб. и доведет свою прибыль до 593 тыс. руб. при расширении производства в 1,5 раза.

Не будем вдаваться в анализ полученных результатов и предос­тавим читателю самому объяснить их экономический смысл. По­путно предлагаем ответить на ряд вопросов: 1) какой внутрипроизводственный механизм оказывает столь сильное влияние на вели­чину прибыли? 2) всегда ли найденная закономерность изменения прибыли будет иметь место в производстве, и если нет, то какой исходный параметр и на какую величину надо изменить, чтобы за­кономерность формирования прибыли превратилась в свою пря­мую противоположность? 3) в каких видах производства можно с успехом применять столь оригинальный метод обогащения?

Такие неожиданные результаты можно получить в практике функционирования предприятий довольно часто, в том числе вследствие Изменения структуры продукции. Поэтому использова­ние параметрической модели может предотвратить нерациональ­ные планово-управленческие решения, сберечь предприятиям зна­чительные средства, уберечь от непредусмотренного ущерба.

4.10. 3оны принятия планово-управленческих решений

Каждое принятое, а затем и реализованное управленческое ре­шение приводит к определенным экономическим результатам, из которых наиважнейшим является показатель прибыли. Ни одно предприятие, фирма не останется равнодушным к вопросу о том, какая у них ожидается прибыль. Она может быть такой же или больше той, что была в базовом периоде, или понизиться, достиг­нув нулевого значения. Наконец реальной для каждой производственно-структурной единицы может оказаться ситуация, когда при­быль становится отрицательной, а производство убыточным.

Следовательно, можно четко выделить три основные зоны экономического состояния любого предприятия: 1) прибыль положительна и растет (I > 1); 2) прибыль положительна, но при этом уменьшается (0 < I <1); 3) прибыль уменьшается и стала отрицательной (I < 0).

Между этими зонами имеются границы, которые однозначно определяются количественно. Так, граница между первой и вто­рой выделенными зонами четко определяется индексом прибы­ли I = 1, а граница между второй и третьей зонами проходит при величине индекса прибыли I = 0.

Принимая то или иное планово-управленческое решение, нужно сразу стремиться к такому варианту, у которого индекс прибыли будет попадать в определенную, заранее выбранную зону. Что для этого необходимо? Прежде всего задаются показа­тели работы предприятия в базовом периоде. Они известны, по­скольку факт прошлого производства уже свершился, и, стало быть, установить их не представляет особого труда. Такими по­казателями являются коэффициент рентабельности производст­ва p и коэффициент переменных затрат r. Затем выясняется, предполагается ли модернизация производства (реконструкция, техническое перевооружение, расширение и пр.), и если нет, то принимается показатель f = 0, а если да — то f > 0.

После этого остаются три прибылеобразующих параметра: коэффициент изменения цены товара d, коэффициент измене­ния себестоимости продукции g , коэффициент изменения объе­ма производства продукции b. Один из этих параметров жестко задается в процессе принятия решения, а два других составляют, так называемую ключевую пару. Параметры, их составляющие, взаимосвязаны: изменение одного параметра влияет на величину другого. Следовательно, эти параметры будут соотноситься меж­ду собой как аргумент и функция. Это и дает возможность оп­ределить значения координат точек, совокупность которых со­ставит границу соответственно между первой и второй, а также между второй и третьей зонами.

Итак, два параметра из трех рассматриваемых принимаются в качестве ключевых. Поэтому здесь возможны три различных комбинации ключевых параметров из трех имеющихся: сочета­ние цены d и объема производства b, сочетание цены d и затрат g, и сочетание затрат g и объема производства b.

За основу рассмотрения примем первый вариант сочетания клю­чевых параметров, ибо именно он представляет наибольший практи­ческий интерес. Поэтому в дальнейшем объектом нашего внимания становятся ключевые прибылеобразующие параметры d и b.

С помощью параметрической модели типа 4.6, задав парамет­ры p, r, I и g, определим координаты точек кривых, которые будут находиться между первой, второй и третьей зонами, являясь при этом границами между ними (рис. 4.4).

Смысл выделенных зон тот же, что и для прошлых рисунков. Первая зона — зона рентабельного производства, в которой прибыль, по сравнению с базовым периодом, возрастает. Вторая ― зона — зона падения прибыли,  хотя производство остается рен­табельным. И наконец, третья зона — зона убыточного произ­водства.

Внутри одной из указанных зон (в зависимости от того, ка­кой индекс прибыли будет задан) можно построить кривую без­различия. Все точки этой кривой будут соответствовать задан­ному индексу прибыли.

Приняв то или иное значение коэффициента изменения це­ны, можно определить объем производства и реализации про­дукции, который и должен обеспечить заданную величину ин­декса прибыли.

Например, если принять p = 1,15,  r = 0,5,  g = 1, I = 1,7, то, как видно из рисунка, можно взять любое сочетание параметров ключевой пары, а именно: 

при d= 1,1 →  b = 0,987;

при d= 1,0  →  b = 1,16;

при d= 0,95 → b = 1,274;

при d= 0,85 → b = 1,581 и т.д.

 

Рис. 4.4. Зоны принятия планово-управленческих решений:

p = 1,15;     r  = 0,5;       g = 1

В таких сочетаниях и будет обеспечиваться заданный индекс прибыли I = 1,7. Объем производства, который при заданной цене обеспечивает искомую прибыль, обозначим b_п .

Но каждое предприятие, как известно, обладает определенной производственной мощностью, и этот объем производства, кото­рый будет соответствовать мощности предприятия, обозначим b_м.

Наконец, объем производства, при котором эффективность капитальных вложений, направленных на получение заданной прибыли, будет не ниже фирменного норматива, обозначим b_э.

Итак, есть величина производственной программы b_п, кото­рая задается исходными условиями, и есть два ограничения b_м и b_э. Как соотносятся все эти три значения объема производства в различных условиях производства — знать крайне необходимо. Это чрезвычайно важная информация, использование которой при выработке планово-управленческих решений позволит из­бежать ошибок.

Все возможные соотношения между указанными объемами рассмотрены и проиллюстрированы на рис. 4.5. Всего оказыва­ется четыре случая разных соотношений.

Первый случай — b _м  < b_n  < b_э .

Второй случай — b _n   < b_м  < b_э .

Третий случай —  b_n    < b_э    < b_м.

Четвертый случай: —  b_э  < b_n  < b_м .

 

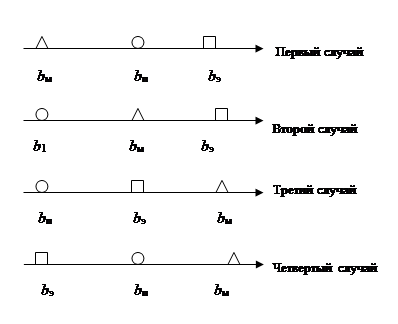
Рис. 4.5. Ограничения в управленческих решениях

по объему производства продукции

 

Вполне очевидно, что самым лучшим и приемлемым реше­нием будет такое, когда производственная программа по прибыли окажется, с одной стороны, больше минимальной границы эффективности, а с другой — меньше производственной мощ­ности предприятия. Такому условию соответствует только четвёртый случай. Его характерная особенность заключается в том, что точка, соответствующая необходимой производственной программе и обеспечивающая заданную прибыль, находится внутри зоны возможного принятия решения. Данная точка обладает большей эффективностью, чем установлено нормативом фирмы, но одновременно она находится внутри производствен­ных возможностей предприятия по его мощности.

Остальные случаи (первый, второй и третий) по каким-то условиям не удовлетворяют заданным ограничениям. Например, производственная программа не может быть больше производ­ственной мощности предприятия (первый случай), производственная программа не должна быть меньше объема производства по заданной его эффективности (третий случай), но производст­венная мощность предприятия не должна быть меньше программы предприятия, обусловленной его эффективностью (вто­рой случай).

Итак, стало быть, единственной зоной приемлемого планово-управленческого решения является такая зона, у которой производственная программа по эффективности производства b_э всегда меньше производственной мощности b_м . Внутри этой зоны будет находиться точка принимаемой производственной программы, через которую проходит кривая безразличия. Эта точка должна быть эффективностью, определяемой следующим выражением:

                               (4.24)

где Е — коэффициент экономической эффективности капи­тальных вложений, направляемых в реализацию проекта по развитию и расширению производства и обеспечивающих заданную прибыль;

I — индекс прибыли, задаваемый проектом;

q — доля базовой прибыли, направляемая в качестве капи­тальных вложений в развитие производства и на прирост прибыли

                                                                                 (4.25)

                                    

К —  капиталовложения в проект;

П_d — величина базовой прибыли;

е — средневзвешенная норма налогообложения прибыли предприятия, %;

h — платежи за используемый банковский кредит, %;

Е_ф — фирменный норматив экономической эффективно­сти капитальных вложений.

Пример.  Предприятие,  имеющее  следующие  исходные  дан­ные  — p = 1,15, r-=0,5 и g = 1,0, запланировало получить индекс прибыли I  = 1,7, установив при этом цену товаров d = 0,95. Расче­ты по модели типа 4.6 показали, что в этом случае производствен­ная программа предприятия должна быть на уровне b_n = 1,274. Производственная мощность предприятия  b_м   = 1,35.              

Предприятие установило для себя норматив эффективности Е_ф = 0,67. Действующая норма налогообложения прибыли е = 35%, платежи банку за используемый кредит h = 30%. Доля базовой прибыли, направляемая на капитальные вложения со­ставляет q = 0,4.

По исходным данным определим по формуле 4.24 эффек­тивность капитальных вложений:

Полученный результат говорит о том, что производственная мощность предприятия b_n = 1,274, обеспечивающая ему индекс прибыли I = 1,7,  обладает эффективностью большей, чем заложено фирменным нормативом (т.е. 0,8375 > 0,67). Это значит, что b_э  <  b_n следовательно, рассматриваемый вариант отвечает четвертому случаю. Соответствующая ему точка лежит внутри  зоны возможного и целесообразного решения.

Построение аналогичных зон и просчет разных вариантов гарантирует предприятию получение такого планово-управленческого решения, которое во всех отношениях обеспечит ему необходимую достаточность, стабильность и надежность.

4.11. Параметрическое прогнозирование прибыли в производственно-хозяйственной деятельности предприятия

В условиях рыночной экономики роль планирования не только не уменьшается по сравнению с планово-директивной  распределительной экономической системой, а, наоборот, многократно возрастает. Особенно это касается внутрифирменного планирования, которое реализуется посредством разработки так называемого бизнес-плана.

Структура бизнес-плана не стандартизирована и носит по сути дела произвольный характер, учитывающий особенности каждого предприятия, выпускаемую им продукцию, состояние рынка и другие обстоятельства. Однако можно перечислить не­которые разделы бизнес-плана, которые, являются основопола­гающими и составляют единое целое. Это и позволяет рассмат­ривать разработанный бизнес-план как системный планово-управленческий документ.

Такими основополагающими разделами являются следующие.

1. Подведение итогов (резюме).

2. Описание производимого товара (оказываемых услуг).

3. Оценка рынка сбыта.

4. Конкуренция и конкуренты.

5. Стратегия маркетинга.

6. План производства.

7. Организационный план.

8. Юридический план.

9. Оценка риска и страхование.

10. Финансовый план.

11. Стратегия финансирования.

Все разделы такого типового плана тесно взаимосвязаны, и каждый последующий, как правило, опирается на один или не­сколько предыдущих разделов.

Разработанный бизнес-план должен отвечать на такие во­просы: 1) что и в каком объеме предприятие будет производить и плановом периоде; 2) какие ресурсы (материальные, техниче­ские, топливно-энергетические, рабочая сила, финансовые) ему для этого нужны; 3) что необходимо предпринять, чтобы вы­полнить намеченную программу; 4) как обезопасить себя от возможных неудач и разорения.

Важнейшим разделом бизнес-плана, в котором аккумулиру­ются практически все результаты предыдущих разделов, являет­ся финансовый план. В нем отражается итог деятельности пред­приятия, его конечный результат. Своими итоговыми оценками этот раздел плана как бы венчает многотрудную и объемную плановую работу.

Разумеется, главное в этом разделе — планирование прибы­ли предприятия. Идея и методология разработки плана по при­были вкратце может быть изложена и проиллюстрирована на рис. 4.6.

Себестоимость продукции складывается под влиянием двух групп   затрат — переменных   (пропорциональных) и условно-постоянных. И если первая группа затрат нарастает с увеличением объема производства, то вторая в некотором его диапазоне остается неизменной. С ростом производственной программы сумма таких затрат будет увеличиваться. Функция себестоимо­сти всей произведенной продукции на графике (рис. 4.6) будет выглядеть в виде прямой линии 1—1.

Произведенная продукция после ее реализации потребителю по установленным ценам обеспечит предприятию некоторую выручку, причем последняя будет нарастать с увеличением объема произведенной продукции. На графике функция вы­ручки изображена прямой линией, ее положение соответствует линии 2—2.

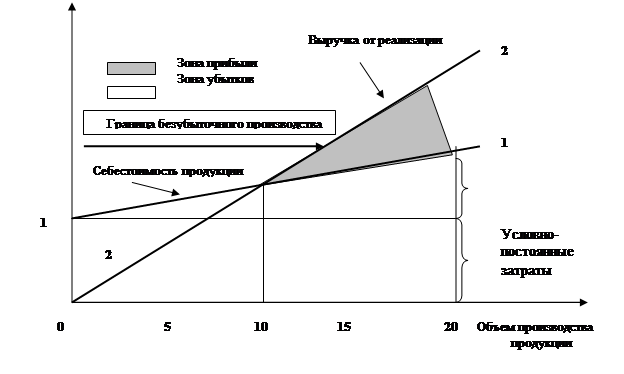Рис.4.6. Граница безубыточности производства продукции

Разница между выручкой от реализации продукции и ее себестоимостью  и  составляет искомую  прибыль  предприятия.

Как видно на графике, эта разница будет вначале отрицатель­ной, что приведет к убыточности производства, а затем, дос­тигнув нулевого значения, станет положительной, перейдя в рентабельное, прибыльное производство (см. соответствующие зоны на графике).

Точка пересечения двух линий 1—1 и 2—2 есть по сути дела точка границы абсолютной безубыточности производства. Ей соответствует определенная производственная программа. Если произведено продукции меньше этой программы, то получается убыток, а если больше — прибыль.

Важно подчеркнуть, что представленная иллюстрация отра­жает лишь идею и методологию определения плановой прибыли, а не рабочую методику. И это понятно, ибо из самого описания видно, что, кроме объема производства продукции, остальные параметры прибыли приняты постоянными и никак не изменя­ются. Так, остаются без изменения цены реализации продукции, переменная часть затрат на производство, не меняются и услов­но-постоянные затраты, а также не предполагается никаких структурных сдвигов в выпускаемой продукции. На практике, разумеется, так не бывает. Поэтому для планирования прибыли не­обходима особая, рабочая методика ее определения.

Подобная методика должна учитывать такие особенности, как:

• возможность изменения цены реализации продукции как в одну, так и в другую сторону. Ведь принятые в бизнес-плане стратегии маркетинга могут быть весьма разнообразными и пре­дусматривать, например, при низких ценах производство и реа­лизацию большего объема продукции или, наоборот, при высо­ких ценах продажу потребителям меньшего ее количества;

• изменение под влиянием многочисленных причин прямых переменных затрат предприятия. Они могут изменяться, напри­мер, когда меняются цены на используемое сырье, материалы, комплектующие, на топливо и энергию, на оборудование, а также расходы на заработную плату основных производственных рабо­чих и т.п., когда под влиянием научно-технического прогресса изменяется расход всех видов ресурсов на единицу выпускаемой продукции;

• изменение условно-постоянных затрат, которые могут быть направлены на совершенствование системы управления предприятием и отдельными его подразделениями, на измене­ние организационной и производственной структуры и пр.;

• возможность модернизации производства, его развитие, расширение и совершенствование. Все это может быть реали­зовано посредством реконструкции предприятия и его техни­ческого перевооружения, переоснащения, ведущего в конеч­ном счете к изменению производственной мощности пред­приятия;

• учет структурных сдвигов продукции, т.е. снятие с произ­водства устаревших, бесперспективных, не пользующихся доста­точным спросом видов продукции и освоение производством прогрессивных моделей, образцов, видов;

• оценка изменений с позиций имеющихся в производстве ограничений по: допустимой эффективности капитальных вло­жений, спросу продукции на рынке, допустимому уровню хо­зяйственного риска, предельному значению уровня относитель­ной безубыточности и т.п.;

• существующая дискретность производства, многономенк­латурный, многоассортиментный его характер. Все изменения, о которых речь шла выше, относятся не ко всей продукции во­обще (такого в жизни и в производстве не бывает), а к кон­кретным ее видам и моделям. По одним видам продукции изменения имеют место, по другим никаких изменений не планируется и т.д.

Только простой перечень условий, которым должна удовлетворять рабочая методика планирования прибыли, свидетельст­вует о том, что эта методика должна быть не просто схемой, го­лой идеей, а обладать свойствами гибкости, комплексности, экономичности, и очень важно — свойством дискретности. По­следнее позволяет установить границы, в рамках которых может и будет находиться одно из возможных и допустимых планово-управленческих решений. Только в этом случае бизнес-план бу­дет научно и экономически обоснованным и станет подлинным руководством в выборе оптимального направления движения и развития фирмы в условиях рынка.

Рабочая методика планирования прибыли предприятия, учи­тывающая все перечисленные условия, ее принципиальная блок-схема представлена на рис. 4.7, где весь процесс включает в себя шесть этапов.

Первый этап — формирование исходной информации.

Второй этап — определение самой прибыли и важнейших экономических и финансовых показателей деятельности предприятия.

Третий этап — анализ полученной информации для опреде­ления приемлемости принятого варианта.

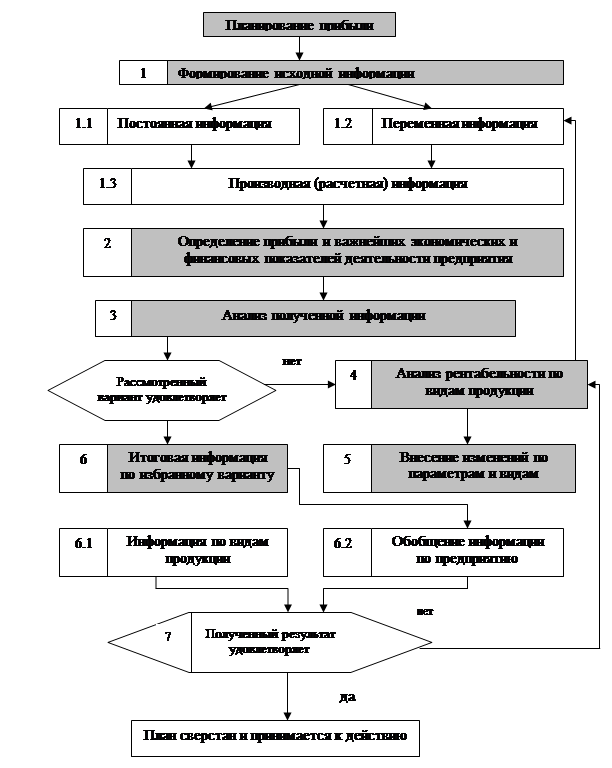Рис. 4.7. Логическая блок-схема алгоритма планирования прибыли

 

Четвертый этап — анализ рентабельности производства по видам продукции, нацеленный на выявление и последующую реализацию резервов повышения прибыли.

Пятый этап — внесение изменений в технику и технологию, организацию производства и управления по видам продукции с целью повышения прибыли.

Шестой этап — принятие решения с учетом всей информа­ции по видам продукции и обобщенной информации — по предприятию в целом.

Остановимся на некоторых этапах подробнее. 

Раскроем содержание первого этапа, где речь идет об ин­формации для планирования прибыли.

Без информации, как известно, никакой процесс управления невозможен. Нельзя, разумеется, и спланировать будущую дея­тельность с достаточной надежностью, почти нереально выбрать лучший вариант планово-управленческого решения. Поэтому с информационного обеспечения практически начинается плано­вая работа.

Если вести речь об информации как о средстве достижения поставленной цели, то ее можно расчленить на три группы, ка­ждая из которых имеет свои источники формирования, а вместе они составляют единое целое, являющееся исходной информа­цией, необходимой и достаточной для того, чтобы решать пла­новые задачи.

Первая группа — постоянная информация, которая не изме­няется в силу того, что отражает базовый период, уже свершив­шийся, о котором известно практически все, что необходимо знать для управления производством и планирования предстоя­щей деятельности.

К постоянной информации планово-управленческого направ­ления можно отнести следующие показатели базового периода:

• общее количество номенклатурно-ассортиментных пози­ций выпускаемой продукции;

• общие годовые текущие затраты предприятия на произ­водство и реализацию выпущенной продукции;

• количество произведенной и реализованной продукции по каждой номенклатурно-ассортиментной позиции в натуральном выражении;

• средневзвешенная цена реализации единицы продукции каждой номенклатурно-ассортиментной позиции;

• прямые переменные (пропорциональные) затраты на про­изводство единицы продукции каждой номенклатурно-ассорти­ментной позиции.

Вторая группа — переменная информация. Она относится к анализируемому периоду и может многократно изменяться в про­цессе поиска лучшего варианта планово-управленческого решения.

К переменной информации анализируемого периода относятся:

• общефирменное изменение условно-постоянных затрат;

• вся вышеперечисленная информация базового периода (только по наименованиям, а не числовая);

• изменения прямых переменных затрат на производство еди­ницы продукции каждой номенклатурно-ассортиментной позиции;

• изменения условно-постоянных затрат при производстве единицы продукции каждой позиции;

• капитальные вложения в совершенствование производства продукции по каждой позиции.

Третья группа — информация производная, получаемая в ре­зультате обработки информации первой и второй групп. При этом информация данной группы чрезвычайно важна, ибо именно она используется для поиска лучшего планово-управ­ленческого решения.

К числу показателей этой группы информации относятся все те показатели, которые используются при расчете прибыли с применением модели типа 4.5 или 4.6.

Рассчитанная по соответствующим формулам производная информация используется затем для определения прибыли предприятия, последующего анализа избранного варианта и пе­ресмотра технических и хозяйственных решений применительно к отдельным видам производимой продукции (разумеется, если это потребуется).

Проведя все поэтапные операции в строгом соответствии с вышеизложенной методологией, окончательно останавливаются на конкретном плане производства продукции. При этом на за­ключительном этапе рассчитываются все важнейшие показатели деятельности предприятия, включая показатели выручки, при­были, величины переменных затрат, рентабельности производ­ства, эффективности производства и др. На этом заканчивается планирование прибыли.

Вопросы для самопроверки и самоконтроля

1. Какой критерий планово-управленческого решения дол­жен применяться в современном бизнесе?

2. Какие резервы повышения прибыли фирмы вы можете на­звать? Как они дифференцируются?

3. Какие факторы и пути повышения прибыли фирмы им знаете?

4. Какие еще, кроме прибыли, могут применяться критерии принятия решений в бизнесе? В каких случаях ими можно вос­пользоваться?

5. Какие ограничения действуют в бизнесе при выработке планового решения?

6. Как получить многопараметрическую математическую модель индекса прибыли предприятия? Попробуйте повторить ее вывод.

7. Какие параметры прибыли представлены в математиче­ской модели?

8. Как перейти от однономенклатурного к многономенклатурному производству при определении индекса прибыли фирмы?

9. Укажите, как влияют на индекс прибыли предприятия от­дельные параметры модели.

10. Какую роль играет графика для познания и понимания закономерностей изменения прибыли и выработки стратегии фирмы?

11. Что такое абсолютная и относительная безубыточность |производства?

12. Как определить границы безубыточности производства?

13. Что собой представляет неопределенность рыночной ситуации?

14. Можно ли предвидеть такую ситуацию?

15. Как можно повысить надежность планового решения?

16. Что из себя представляют страховые коэффициенты?! Какую роль они могут исполнить? Как их можно рассчитать?

17. Какой смысл имеет изучение компенсационных соотношений прибылеобразующих параметров?

18. Какая пара параметров модели представляет для бизнеса; наибольший интерес с точки зрения компенсационных соотношений?

19. Какой количественной связью объединены параметры изменений объема производства и цены товара?

20. Какое практическое значение для бизнеса имеет знание компенсационных соотношений между объемом производства и ценой товара?

21. Какие методы можно применить в бизнесе с целью рас­ширения производственной мощности и развития предприятия?

22. Какие текущие затраты изменяются при расширении производственной мощности предприятия?

23. По какой закономерности изменяются переменные и по какой — условно-постоянные затраты предприятия при расши­рении его производственной мощности?

24. Какие возможности открываются для бизнеса в связи с расширением производственной мощности предприятия? Как можно использовать эти возможности и при каких условиях?

25. Для чего нужно оценивать влияние каждого параметра на конечный результат?

26. Каким методом лучше всего осуществить процедуру опре­деления влияния отдельных параметров на конечный результат?

27. Как можно впоследствии использовать полученную ин­формацию о влиянии отдельных параметров модели на конеч­ный результат производства?

28. Какие варианты структурных сдвигов продукции вы мо­жете указать?

29. Какую серьезную погрешность можно допустить, если не провести необходимых расчетов по определению влияния струк­турных сдвигов на прибыль предприятия?

30. Отчего может возникнуть серьезная погрешность в оцен­ке результатов структурных сдвигов продукции?

31. Как практически можно использовать в бизнесе резуль­таты анализа структурных изменений продукции?

32. Какие зоны экономического состояния предприятия можно выделить?

33. Каковы количественные границы между экономически­ми зонами состояния предприятия?

34. Как связаны экономические зоны состояния предпри­ятия с его производственной мощностью, с производственной программой и с величиной капитальных вложений в реконст­рукцию и модернизацию предприятия?

35. Как оценить эффективность капитальных вложений и целесообразность их использования для реконструкции пред­приятия?

36. На какие важнейшие вопросы должен ответить разраба­тываемый бизнес-план предприятия?

37. В чем заключается основная идея определения и плани­рования прибыли предприятия?

38. Перечислите основные требования, которые предъявляют­ся к рабочей методике по планированию прибыли предприятия.

39. Укажите этапы алгоритма планирования прибыли пред­приятия.

Глава 5.     Рыночное моделирование и оптимизация

                        планово-управленческих решений

При переходе к рынку предприятия России столкнулись с мас­сой проблем, решить которые все разом оказалось большинству из них не под силу. Это привело к сильнейшему спаду производства, экономическому, финансовому и управленческому кризису.

Вопрос о том, как работать в условиях рынка, как управлять предприятием и принимать решения, еще долгое время останет­ся актуальным. Все дело в том, что отечественные предприятия не имеют практически никакого опыта работы в рыночной эко­номике. Они не располагают достаточной информацией, не знают, какая информация им необходима, как ею пользоваться, как накапливать, обрабатывать и использовать полученные све­дения в принятии управленческих решений.

К сожалению, экономическая литература, выпускаемая в нашей стране, носит описательный характер. Трудно встретить конкретные рекомендации по расчету маркетинговых показате­лей, практически отсутствуют математические модели, с помо­щью которых можно рассчитать цены на товары, объемы их производства, прогнозы прибыли, выручки и т.п.

Все эти вопросы стали предметом рассмотрения в данной главе.

5.1. Спрос, предложение, цена товара

Поступающий на рынок товар может пользоваться у потреби­телей большим или меньшим успехом, или, как говорят, большим или меньшим спросом. Спрос на товар — понятие рыноч­ное. С ним связаны практически все рыночные категории, регу­ляторы и механизмы производства. Это ключевое понятие ры­ночной экономики. Оно означает желание и способность покупа­телей приобрести (купить) конкретный товар. Спросом можно назвать количество товара определенного качества и назначения, которое будет куплено потребителями в данном временном ин­тервале по конкретной цене.

В рыночной экономике действует закон спроса. Он гласит, что величина покупательного спроса обратно пропорциональна цене товара при прочих равных условиях. Следовательно, при повышении цены товара спрос на него сокращается, а при сни­жении цены спрос растет (рис. 5.1).

 

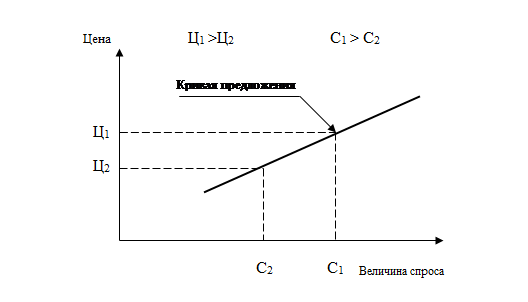
Рис. 5.1. Действие закона спроса

Как видно из рисунка, в соответствии с законом спроса при цене Ц₁ спрос С₁, а при цене Ц₂ спрос С_2.  При этом Ц₁ >Ц₂ ,  а С₁  < С_{2 .}  Линия, в соответствии с которой изменяется величина спроса под влиянием изменения цены товара, называется кривой спроса. Для каждого конкретного товара она имеет свою форму и свой наклон к осям координат.

Закон спроса универсален и действует (при прочих равных условиях) практически всегда, за одним лишь исключением: оно касается ажиотажного спроса, возникающего в ожидании по­вышения цен на товар. В таком случае описанная закономер­ность нарушается, и спрос на товар возрастает, несмотря на по­вышение цен.

Не менее важным понятием рыночной экономики является понятие предложение товара.

Предложение — это желание и способность продавцов предоставить товары для продажи на рынке. По сути дела предложение представляет собой количество товаров, которое произво­дители готовы продать по определенной цене в данном временном интервале.

В рыночной экономике действует закон предложения, со­гласно которому предложение при прочих равных условиях из­меняется в прямой зависимости от изменения цены. Это значит, что по мере роста цен производители предлагают к продаже большее количество товаров, а при снижении цен — меньшее количество товаров (рис. 5.2).

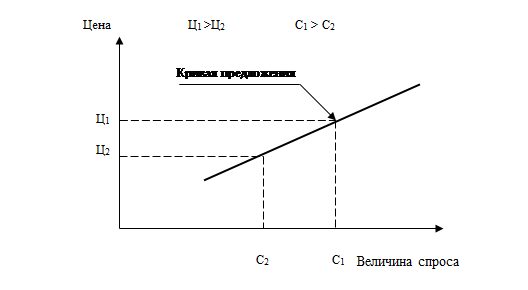
Рис. 5.2. Действие закона предложения

Как видно из рисунка, при Ц₁ >Ц₂ имеет место С₁> С_{2 .} Линия, в соответствии с которой изменяется величина предло­жения под влиянием изменения цены товара, называется кривой предложения.

Направление изменения предложения товара от изменения цены на него объясняется двумя причинами. Во-первых, пред­приятия включают в производство резервные мощности, прово­дят модернизацию, реконструкцию и техническое перевооруже­ние производства, с тем чтобы произвести и продать больше то­варов, цены на которые в данный момент высоки. Во-вторых, предприятия других отраслей срочно начинают осваивать про­изводство тех товаров, цены на которые столь высоки.

Однако изменение предложения на рынке не может проис­ходить мгновенно, по мере повышения цены товара. Это требует определенного времени, в течение которого производство от­реагирует на конъюнктуру рынка соответствующим образом.

Закон предложения так же универсален, как и закон спроса, но и у него есть исключение: он не будет действовать, если в недалеком будущем ожидается падение спроса на данный товар. Тогда фирмы не будут стремиться увеличивать производство данного товара в будущем, если даже цены на него растут в на­стоящем времени.

Итак, спрос и предложение товара встречаются на рынке. Их совместное взаимодействие представлено на рис. 5.3.

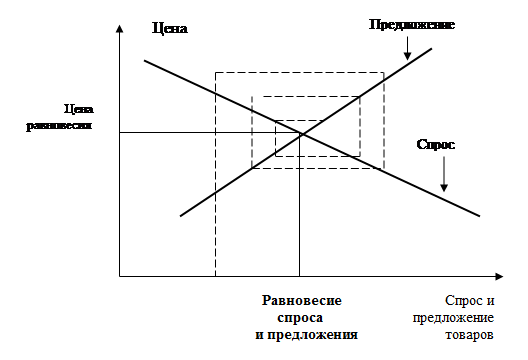
Рис.5.3. Формирование цены равновесия спроса и предложения

 

Представим, что на рынке появился новый товар. Объем его производства и продаж вначале незначителен, ибо очень высока цена, поэтому спрос на данный товар значительно превышает предложение. Учитывая сложившуюся конъюнктуру рынка, про­давцы поставят для покрытия дефицита дополнительное количе­ство данного товара. Тогда предложение превысит спрос и цена товара упадет.

Как только это произойдет, количество товара на рынке со­кратится, и цикл колебания цен повторится. При этом колеба­ния цен относительно некоторой стабильной величины с каж­дым новым циклом будут сокращаться, закручиваясь в спираль. Это будет продолжаться до тех пор, пока не установится равно­весие между спросом и предложением товара (точка равнове­сия). Цена товара в этой точке называется ценой равновесия. Она довольно быстро устанавливается на рынке и с небольшими колебаниями может существовать длительное время, обеспечивая равновесие между спросом и предложением товара.

Таким образом, в рыночной экономике не издержки произ­водства формируют цены товаров, а соотношение спроса и предложения товаров. Поэтому цена может быть больше издер­жек производства, равна им и меньше издержек. Она стремится к такому уровню, при котором спрос будет больше предложе­ния, т.е. если товар в дефиците, то цена на него будет высокой; если предложение превысит спрос, то цена упадет.

Однако все это будет справедливо в процессе регулирования спроса и предложения, когда они выступают в качестве функ­ции цены товара (спрос превышает предложение — цена больше равновесной при сложившемся дефиците товара; спрос меньше предложения — цена меньше равновесной при сложившемся излишке товара).

Но цена также может выступать регулятором спроса и пред­ложения товара, когда соотношение между ними является функцией цены (рис. 5.3). Ведь в рынке все товаропроизводите­ли свободны в политике установления цен на свои товары. И если, игнорируя законы рынка, продавцы установят цены своих товаров выше равновесной цены, то это приведет к появлению излишка продукции (предложение превысит спрос), а если, на­оборот, продавцы установят на свой товар цену ниже равновес­ной цены, то это создает на рынке дефицит продукции (пред­ложение окажется меньше спроса). В конечном счете продавцы не захотят оставаться в убытке и путем корректирования цен на свои товары придут к равновесной цене.

Вместе с тем не только цены могут регулировать спрос и предложение товаров на рынке. Такую роль выполняют и дру­гие, неценовые факторы регулирования: доходы потребителей, качество товаров, расходы производителей и др. Поэтому следу­ет различать такие понятия, как «изменение величины спроса» и «изменение спроса», «изменение величины предложения» и «изменение предложения» и некоторые другие термины.

Изменение величины спроса — это изменение количества товара, которое потребители хотят и могут купить, происходящее в резуль­тате изменения цены товара (движение вдоль кривой спроса).

Изменение спроса — изменение количества товара, которое покупатели желают и могут купить, происходящее вследствие изменения неценового фактора (сдвигом кривой спроса).

Изменение величины предложения — изменение того количе­ства товара, которое производители желают и могут продать, происходящее в результате изменения цены товара (движение вдоль кривой предложения).

Изменение предложения — изменение количества товара, ко­торое производители желают и могут продать, происходящее в результате изменения неценового фактора (сдвиг кривой пред­ложения).

Различия в этих понятиях представлены на рис. 5.4 и 5.5. Кро­ме отмеченных различий имеются различия в понятиях товара.

Взаимозаменяющие товары (субституты) — такие пары това­ров, для которых рост цены одного товара приводит к росту спроса на другой товар.

Взаимодополняющие товары (комплементы) — пары товаров, для которых рост цены одного товара приводит к падению спроса на другой товар.

Нормальный товар — товар, спрос на который растет при росте потребительских доходов.

Низший товар (товар низкого качества) — товар, спрос па который падает при росте потребительских доходов.

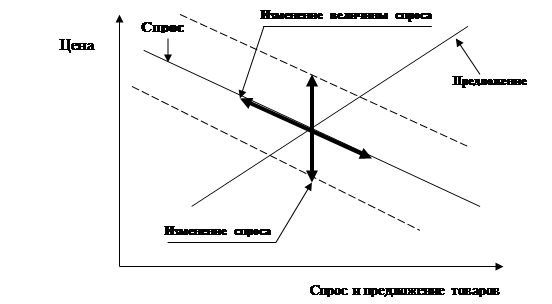
Рис. 5.4. Влияние изменения спроса и его величины на цену товара

 

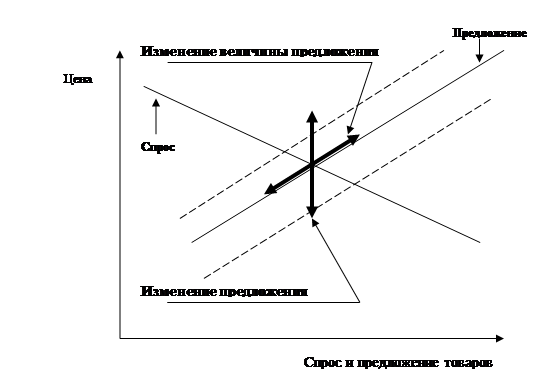
Рис. 5.5. Влияние изменения предложения

 и его величины на цену товара

Сдвиги кривых спроса и предложения происходят по сле­дующим причинам (табл.5.1).

5.2. Эластичность спроса и предложения товара

Опыт существования рыночных отношений свидетельствует о том, что спрос на отдельные товары не остается постоянным, а подвержен изменениям. Это связано в основном с действием ценовых и неценовых факторов, из которых наибольшая роль принадлежит доходам и платежеспособности потребителей. Ес­тественно, чем ниже цена товара и выше доходы потребителей, тем больше спрос на товар (при прочих равных условиях).

Таблица 5.1

Причины сдвига кривых спроса и предложения

Причина сдвига	Направление сдвига
левый	правый
Кривые спроса
Рост цен замещающего товара		+
Понижение цены замещающего товара	+
Рост цены дополняющего товара	+
Понижение цены дополняющего товара		+
Рост дохода потребителя (низкий товар)	+
Снижение дохода потребителя (низкий товар)		+
Рост дохода потребителя (нормальный товар)		+
Снижение дохода потребителя (нормальный товар)	+
Предпочтение товара покупателями растет		+
Предпочтение товара покупателями падает	+
Изменен   Изменение потребительских ожиданий по поводу бу­дущего состояния рынка. Наприме   Например: усиление инфляционных процессов, появление более качественного продукта		+
+
Кривые предложения
Рост цен на ресурсы (рабочая сила, сырье и т.п.)	+
Понижение цен на ресурсы		+
Появление новой техники, сокращающей затраты на производство		+
Рост цены товара, производимого из тех же ресурсов, что и данный товар	+
Понижение цены товара, производимого из тех же ре­сурсов, что и данный товар		+
Изменение ожиданий производителя по поводу буду­щего состояния рынка. Например: усиление инфляционных процессов, повышение деловой активности	+
	+

Исследуя спрос и потребление различных товаров в семьях рабочих и служащих, крупный  немецкий ученый-социолог Э. Энгель в середине XIX в. установил, что в принципе спрос на товары в зависимости от цен на них и доходов потребителей подчиняется строго определенной закономерности (рис. 5.6).

Первая группа товаров — это в основном продукты питания (кроме деликатесов) и товары первой необходимости (верхняя часть рисунка). Спрос на них по мере снижения цен и повы­шения доходов потребителей вначале очень быстро растет, но постепенно замедляется по мере насыщения рынка этими то­варами и повышения уровня благосостояния потребителей. Наступает момент, когда спрос на них стабилизируется. Зако­номерность изменения спроса характеризуется для этих това­ров кривой А.

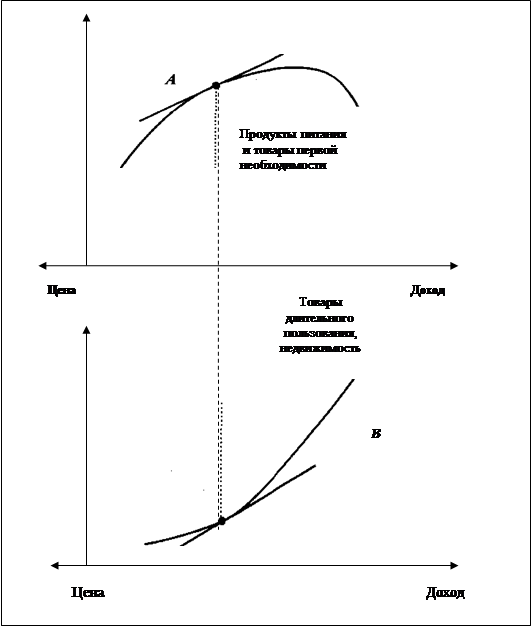
Рис. 5.6. Закономерность измерения эластичности спроса товаров

Иначе ведет себя спрос на товары длительного пользования (электробытовые приборы, радиоприемники, телевизоры, мото­циклы, автомобили и т.п.), деликатесные продовольственные товары и недвижимость. Здесь прямо противоположная законо­мерность: вначале спрос очень незначителен, а затем быстро на­растает по мере повышения благосостояния потребителей (кри­вая  В   в нижней части рисунка).

Таким образом, спрос на товары — категория не только рыночно-экономическая, но и историческая. В каждый историче­ский момент изменяются и спрос, и темпы его изменения под влиянием снижения цен на товары и роста доходов потребите­лей. Изменение темпов величины спроса определяется углом наклона касательной в точке кривой спроса к оси дохода или цены. В количественном выражении этот показатель измеряется коэффициентом эластичности спроса соответственно либо от цены, либо от дохода.

Коэффициент эластичности спроса от цены, или ценовая эластичность, показывает, на сколько процентов изменится спрос на товар при изменении его цены на 1%. Исчисляется этот коэффициент по формуле

                                (5.1)

где К_эц — коэффициент эластичности спроса от цены товара;

Y — спрос на товар в единицу времени;

∆Y — изменение спроса под влиянием изменения цены;

X — цена товара (до ее изменения);

∆X — изменение цены товара.

Если ценовая эластичность больше единицы, то такой товар принято называть высокоэластичным; если меньше единицы — низкоэластичным; если равен единице — товар с единичной эла­стичностью (рис. 5.7).

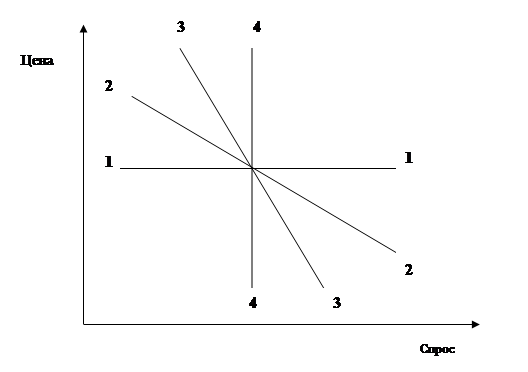
                             1 — 1 совершенно эластичный спрос

2 — 2 высокоэластичный спрос

3 — 3 низкоэластичный спрос

4 — 4 совершенно неэластичный спрос

Рис. 5.7. Ценовая эластичность спроса товаров

Например, коэффициент эластичности спроса от цены К_эц = 3. Такой коэффициент присущ высокоэластичным това­рам. Если продавец на 2% снизит цену на такой товар, то спрос на него возрастет на 6%.

Следует иметь в виду, что эластичность спроса товаров есть величина в силу своей историчности довольно консервативная и не может изменяться по несколько раз в течение дня. Она будет изменяться постепенно, по мере повышения уровня жизни на­рода. Поэтому показатели эластичности спроса для одной стра­ны не будут соответствовать этим же показателям для других стран. Более того, даже внутри одной страны различные регио­нальные рынки могут иметь разные значения коэффициентов эластичности спроса товаров в силу того, что регионы могут развиваться неравномерно, у них могут отсутствовать необходи­мые транспортные связи и т.п.

Теория эластичности применима не только к изучению спроса продукции, но и к предложению товаров. Последнее из­меряется коэффициентом эластичности предложения от цены. Его расчет выполняется по формуле:

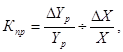                     ( 5.2)

где К_пр — коэффициент эластичности предложения от цены;

∆Y_p — изменение предложения под влиянием изменения цен;

Y_p  — предложение товара в единицу времени.

Следует отметить, что эластичность предложения в огромной степени зависит от времени, которое имеется в распоряжении производителей, чтобы отреагировать на данное изменение це­ны продукта. Чем продолжительнее время, которым располагают производители, тем большей будет эластичность предложе­ния товара (при прочих равных условиях).

Используя теорию эластичности, можно сознательно управлять спросом товаров и ценами на них. Этим неоднократно пользовались и продолжают пользоваться многие товаропроизводители и продавцы продукции.

Зная коэффициент эластичности спроса от цены, можно, например, определить изменение спроса товара при планируе­мом изменении цены или определить изменение цены товара при планируемом изменении спроса на него.

Определить искомые значения этих параметров можно по формулам

                              (5.3)

                                                              (5.4)

Например, если спрос на конкретный товар на рынке со­ставлял y = 100 ед. при цене x = 1000 долл. в единицу времени, то, изменив цену на величину ∆X = 50 долл., можно изменить спрос на этот товар (при коэффициенте эластичности спроса E_d   = 3) следующим образом:

Это значит, что при снижении цены товара спрос на него на рынке увеличится и составит 115 ед., а при повышении цены — понизится и будет 85 ед.

Другой пример. Если использовать исходные данные, то можно установить величину изменения цены товара.

Примем: у = 100 ед., x = 1000 долл., К_эц = 3, ∆y = 15 ед. Тогда изменение цены составит:

Значит, если цена товара будет 1050 долл., то спрос упадет (его величина составит 85 ед.), а если цена снизится и будет 950 долл., то спрос увеличится до 115 ед.).

Большее значение для рыночной экономики имеет связь между спросом товара и доходом потребителей. Она измеряется путем расчета коэффициента эластичности спроса от дохода по формуле

                             (5.5)

где К_эд — коэффициент эластичности спроса товара по дохо­ду потребителей;

Д₀ — доход потребителей;

∆Д — изменение дохода потребителей.

Для большинства товаров величина этого коэффициента является положительной (к ним прежде всего относятся нормаль­ные товары). Но есть и такие товары, для которых этот коэф­фициент может принимать отрицательное значение (низшие то­вары). Спрос на них сокращается (при определенных условиях) по мере роста доходов потребителей. Например, при общих вы­соких доходах потребители при дальнейшем росте доходов начинают сокращать потребление многих пищевых продуктов — хлеба, картофеля, маргарина и пр.

Для нормальных товаров положительная величина эластич­ности по доходу имеет довольно значительный разброс: от вели­чин, близких к нулю, до величин в несколько единиц. Напри­мер, по данным некоторых американских экономистов, в на­стоящее время в развитых странах коэффициент эластичного спроса по доходу для многих продуктов сельского хозяйства со­ставляет +0,2, а для автомобилей +3,0. Разница, как видим, весьма существенная.

Информация о коэффициентах эластичности спроса по до­ходу имеет большое практическое значение. Она позволяет прогнозировать будущее развитие и процветание тех произ­водств, товары которых имеют значительную величину этого ко­эффициента, и, наоборот, застой и сокращение производства тех товаров, для которых эластичность спроса по доходу есть ве­личина незначительная.

Теория эластичности спроса предусматривает также прак­тическое применение так называемой перекрестной эластично­сти. Ее суть заключается в том, что спрос на один конкретный продукт очень часто зависит от изменения цены на другой продукт. Например, спрос на маргарин в огромной степени бу­дет зависеть от изменения цен на сливочное масло (взаимоза­меняемые товары), а спрос на автомобили разного класса — от изменения цен на бензин (взаимодополняющие товары).

Коэффициент перекрестной эластичности спроса определя­ется по формуле

           

                              (5.6)

где К_эп — коэффициент перекрестной эластичности спроса товара Y изменения цены товара X;

X_x — цена товара x;

∆X_x — изменение цены товара.

Если коэффициент перекрестной эластичности есть величи­на положительная, т.е. спрос на товар Y изменяется пропорцио­нально изменению цены на товар X, то товары X и Y являются взаимозаменяемыми товарами. Если коэффициент перекрестной эластичности — величина отрицательная, т.е. спрос на товар Y изменяется обратно пропорционально изменению цены на товар X, то товары X и Y являются взаимодополняющими.

Нулевой коэффициент перекрестной эластичности спроса означает, что между двумя анализируемыми товарами нет ника­кой связи. Например, повышение цен на сливочное масло прак­тически не скажется на изменении спроса на такие товары, как фотоаппараты, автомобили, мебель и т.п.

Теория эластичности спроса очень многогранна. Она охва­тывает практически все действующие на спрос факторы, в том числе уровень качества продукции. Действительно, если какой-то товар пользуется определенным спросом, то повышение уровня его качества (без изменения цены) наверняка несколько увеличит спрос на него. Поэтому можно и нужно говорить об эластичности спроса на товар по уровню его качества. Его можно исчислить по формуле

                                               (5.7)

где К_эк — коэффициент эластичности спроса по качеству то­вара;

К_к — уровень качества товара, исчисленный в объектив­ных, абсолютных или относительных показателях;

∆К_к —  прирост уровня качества товара.

Используя данную формулу и формулу ценовой эластично­сти, можно записать:

 

Отсюда можно получить формулу

 

                                        (5.8)

Она означает, что относительное изменение цены товара при сохранении спроса на него прямо пропорционально изменению уровня его качества и соотношению коэффициентов эластично­сти спроса по качеству и по цене.

Например, если уровень качества товара повысился на 20% (т.е.       ),  а соотношение коэффициентов эластичности спроса     , то цена на такой товар может быть повышена на 30% (). При этом спрос на данный товар сохранится в прежнем объеме.

Если цена на данный товар останется без изменения, то произойдет прирост спроса, который можно определить по формуле

                                          (5.9)

Для условий предыдущего примера, если принять дополнительно  К_эк ⁼ = 1,65, то получим:        

Это значит, что под влиянием повышения качества товара спрос на него при сохранении цены возрастет на 33%.

Все рассмотренные ситуации изменения цен и спроса на различные товары могут быть проиллюстрированы графически (рис. 5.8).

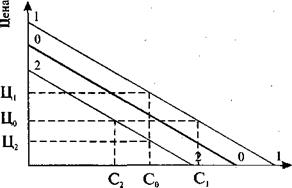
                                                                                          Спрос

Рис. 5.8. Сочетание цен и спроса товаров

 под действием различных факторов

 

Предположим, что кривая спроса на конкретный товар име­ет орбиту 0—0 и точку равновесия спроса и предложения с ко­ординатой Ц₀ — С_{0 .} Допустим далее, что под влиянием роста до­ходов потребителей или повышения качества товара (а также возможного изменения цен на взаимозаменяемые или взаимо­дополняемые товары) точка равновесия переместится на другую орбиту (например, орбиту 1—1 или орбиту 2—2). Тогда цена рав­новесия на товар изменится и будет иметь координату  Ц₁ —C₀. При этом спрос на товар не изменится и составит C₀ .

Но фирмы, производящие этот товар, могут пойти другим путем — оставить цену равновесия на прежнем уровне, т.е. на уровне Ц₀. Тогда им придется изменить объем поставки данного товара на рынок с таким расчетом, чтобы удовлетворить изме­нившейся спрос. А это будет спрос на уровне C₁ или C₂.

Таким образом, познания в области эластичности спроса и предложения товаров позволяют фирмам более точно планиро­вать свою хозяйственную деятельность, принимать обоснован­ные планово-управленческие решения.

5.3. Моделирование цены и спроса на товары

Спрос на продукцию — одно из самых серьезных ограниче­ний объема ее производства, т.е. предложения этих товаров по­требителям. Спрос зависит от очень многих причин: характера продукции, ее важности и значимости для потребителей, от структуры населения (национальной, половой, возрастной, об­разовательной и т.п.), природно-географических и климатиче­ских условий проживания, традиций, культуры, моды и т.д. Все это так называемые внешнеэкономические причины, кото­рые действуют постоянно в отношении какого-то конкретного товара и формируют вполне определенный на него спрос. Его можно установить как бы на некотором уровне, условно при­нимаемом для фиксированного момента времени за единицу. Причем последняя будет изменяться под влиянием экономиче­ских причин. К ним относятся цены на товары (ценовой фак­тор) и ряд других причин, которые хоть и связаны с ценами, но с ценами не на конкретный товар, а на другие товары рын­ка (поэтому условно их называют неценовыми факторами).

В принципе цена товара на рынке может по воле его про­давца изменяться в ту или иную сторону. Это связано с тем, что с помощью цены продавец товара может регулировать спрос на него и тем самым решать свои конкретные задачи на данный момент (например, оказывать давление на конкурентов, стараться избавиться от излишка товаров, или, наоборот, придержать товар от продажи в ожидании повышения цен на него). Причин для такого поведения может быть множество.

Но спрос на товар на самом деле может измениться даже при условии, когда продавец товара не меняет на него цену. Это имеет место тогда, когда в действие вступают неценовые факторы регулирования спроса. Поэтому чрезвычайно важно смоделировать изменения спроса на конкретный товар при одновременном действии всех влияющих на него факторов. Обратимся к рис. 5.9, на котором представлены две орбиты (C₀ и C₁) изменения спроса товара под воздействием ценового фактора (C₀) и неценовых факторов (C₁).

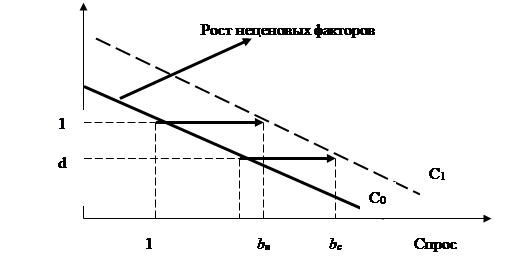
Рис. 5.9. Формирование совокупного спроса под влиянием действия всех факторов

Условно примем цену товара и соответствующий ей спрос в базовом периоде за единицу. Точка, соответствующая этим ус­ловиям, лежит на орбите C₀.

Под влиянием снижения цены от 1 до величины d спрос на данный товар изменится и составит b_ц.

Тогда, используя формулу 5.1, можно записать:

Из этого выражения легко получить следующее уравнение:

                              (5.10)

Например, если К_эц = 2,0 и цена при этом снизится на 5% (т.е. d = 0,95), то легко подсчитать, что спрос на товар составит — b_ц = 1,1, или повысится по сравнению с базовым перио­дом на 10%.

Произведем аналогичную прогнозную операцию с неценовыми факторами. В ее основе можно использовать формулу 5.5, заменив доход потребителей, на совокупный неценовой фактор вообще, куда доход потребителей будет входить одним из со­ставных элементов. Такое выражение можно записать в сле­дующем виде:

где К_эн — коэффициент эластичности спроса товара под воз­действием всех неценовых факторов;

b_н — спрос на данный товар под влиянием одновремен­ного и совокупного действия всех неценовых факторов;

Н — совокупное значение всех неценовых факторов, ко­торое изменялось с единицы (в базовом периоде) до указанной величины.

В результате действия всех неценовых факторов точка 1—1 для базового периода должна переместиться на орбиту C₁ и из­менить свою координату на 1— b_н.

Если преобразовать записанное выше выражение, то можно получить:

                       b_н −1 = К_эн · (H − 1)                               (5.11)

Теперь, когда созданы модели раздельного влияния спроса продукции от ценового и неценового факторов, можно их объе­динить. Для этого нужно левую часть формулы 5.11 добавить в левую часть формулы 5.10. Аналогичную операцию выполнить с правыми частями указанных формул. Тогда получим:

b_ц + b_н − 1 = 1 + К_эц · (1 –d) +  К_эн  · (Н −1).

Но левая часть данного выражения есть спрос на продукцию под действием всех факторов (ценового и неценовых) одновре­менно. Такой спрос, какой вытекает из рис. 5.9, соответствует величине b_с. Эта величина отражает совокупный спрос на дан­ный товар от действия всех факторов и под влиянием совокуп­ного их предложения от всех товаропроизводителей.

Формула, которая отражает эту величину спроса, будет иметь вид:

                 (5.12)

Теперь раскроем поэлементное содержание неценовых факто­ров. Их общую величину можно представить следующим образом:

          (5.1)

где Д — коэффициент изменения дохода потребителей товара по сравнению с базовым периодом;

d_в — коэффициент изменения цены взаимозаменяемого товара;

d_c — коэффициент изменения цены сопрягаемого (взаимодополняемого) товара;

1_к — индекс изменения качества товара по сравнению с базовым периодом;

Н_ф — значение совокупного действия неценовых факторов;

К_эд, К_эв, К_эс, К_эк — коэффициенты эластичности спроса товара соответственно от дохода потребителей, от цены взаимозаменяемого товара, от цены сопрягаемого товара, от изменения качества товара.

Так, если принять d_в = 1 и d_c = 1 (т.е. цены на взаимозаме­няемые и взаимодополняемые товары не меняются), а также Д = 1,1 (доходы потребителей возросли на 10%) и К_эд = 1,15 и ка­чество товара возросло на 15%), то при коэффициентах эла­стичности спроса товара от дохода К_эд = 1,5 и качества продук­ции К_эк = 0,8 влияние неценовых факторов на величину спроса товара составит:

Н_ф = К_эн (Н − 1)= 1,5 · (1,1 − 1) + 0,8 ·  (1,15 − 1) = 0,15 + 0,12 = 0,27 .

Это значит, что только под воздействием неценовых факто­ров спрос на данный товар возрастет по сравнению с базовым периодом на 27%.

Следует еще раз подчеркнуть, что величина спроса, опреде­ляемая по формуле 5.12, соответствует точке равновесия спроса и предложения. То есть предложение товара будет строго соответствовать при данной фиксированной цене и действующих неценовых факторах спросу на данный товар. Но если предло­жение будет больше или меньше спроса на данный товар, то должна измениться и его цена. И лишь тогда вновь установится требуемое соответствие спроса и предложение товара.

Как должна изменяться цена на товар можно определить по следующей формуле, которая выводится из формулы 5.12:

            (5.14)

Это значит, что цена товара может принимать различные значения и изменяться в большом диапазоне; все зависит от предложения товара. Увеличивая или уменьшая предложение товара b_с, можно регулировать его цену, при которой спрос и предложение уравновесятся.

Например, при К_эц = 1,3, Н_ф = 0,12 цена товара составит при b_с = 1→ d  = 1,092 (т.е. цена возрастет на 9,2%); при b_с = 1,05 → d = 1,042 (т.е. цена возрастет на 4,2%); при b_с = 1,2 → d = 0,892 (т.е. цену придется снизить  почти на 12%, чтобы иметь возможность продать весь товар). Ситуация в огромной степени будет зависеть от продавца товара. Если он не изменит цену, не будет гибко реагировать на конъюнктуру рынка, то он либо не продаст весь свой товар (когда цена будет больше тре­буемой для равновесия), либо продаст его значительно быстрее (когда цена будет меньше требуемой).

В теории маркетинга рассматриваются различные стратегии ценообразования, каждая из которых рекомендует свои подходы к решению задачи установления цен на товары, отличающиеся от равновесной цены. Такие рекомендации даны в трудах, на­пример, Ф. Котлера, Дж.Р. Эванса, Б. Бермана и многих других теоретиков маркетинга. Они широко известны и опубликованы в российской литературе. Например, скользящее ценообразова­ние (цены последовательно снижаются с целью охвата различных уровней спроса), проникающее ценообразование (установ­ление цен ниже рыночного уровня с целью увеличить свою до­лю рынка), сегментное ценообразование (установление различ­ных цен на одинаковые продукты на локально изолированных рынках), гибкое ценообразование (установление цен с учетом изменившихся условий на рынке) и т.д.

В основе таких рекомендаций лежат частные локальные про­блемы продавца, которые он пытается решать с помощью из­бранной стратегии маркетинга. Но все же надо отметить, что все известные стратегии так или иначе носят временный характер, и после решения фирмой поставленной задачи происходит плано­вый переход к эластично-равновесному ценообразованию.

5.4. Модели рынка и их признаки

Если попытаться проанализировать все рыночные ситуации, которые реально встречаются на практике, то легко можно об­наружить их бесчисленное разнообразие.

Все многообразие рыночных ситуаций определяется действием многих факторов, например таких, как характер выпускаемой продукции, количество поставщиков сырья, топлива и энергии, количество продавцов аналогичных товаров, транспортные связь между предприятиями и т.п.

Однако  более  глубокий  анализ  может  показать,  что  все встречающиеся факторы носят лишь промежуточный характер. Так  или  иначе  они  реализуются  через  конкуренцию  между предпринимателями. Тип конкуренции,  ее количественные  и качественные признаки окажут результирующее влияние на появление той или иной рыночной ситуации.

Основу рыночных отношений составляет конкретный товар, который становится предметом купли-продажи со стороны двух совокупных субъектов — продавца и покупателя. Совокупный продавец товара одного и того же назначения — это довольно распространенное понятие отрасли. Отрасль может формиро­ваться значительным количеством товаропроизводителей, а мо­жет состоять из одной крупной фирмы. Между этими двумя крайними полюсами могут иметь место любые варианты с различной численностью товаропроизводителей.

Можно ли все это многообразие как-то дифференцировать? Если отказаться от жесткого количественного подхода и постро­ить дифференциацию в чисто качественном плане, то сделать что можно.

Итак, первая ситуация — отрасль состоит из большого коли­чества мелких товаропроизводителей — сотен и даже тысяч. Между ними возникает конкуренция, которую называют чистой конкуренцией, или совершенно конкурентным рынком.

Вторая ситуация — отрасль состоит из нескольких десятков товаропроизводителей. Разумеется, между ними тоже существует довольно острая конкуренция, которая оказывает влияние на возникновение определенной рыночной ситуации. Этот тип рынка называют монополистической конкуренцией.

Третья ситуация — отрасль формируется из нескольких производителей, каждый из которых — довольно крупная фирма. Всего таких фирм 3—4, максимум пять. Такой тип рынка назы­вают олигополией.

Четвертая ситуация — отрасль представлена одним круп­ным товаропроизводителем-монополистом. У него нет конку­рентов, поэтому тип рынка, где он властвует, называют чистой монополией.

Итак, со стороны совокупного продавца на рынке можем быть четыре характерных ситуации, отражающих различные варианты рыночной конкуренции.

Теперь обратимся к совокупному покупателю. Какие варианты рыночных ситуаций возможны здесь? Оказывается, все те же четыре характерные ситуации.

Первая — значительное количество покупателей (тысячи и более).

Вторая — несколько десятков покупателей.

Третья — покупателей от двух до десятка.

Четвертая — один покупатель-монополист.

Различные сочетания рыночных типов со стороны продавцов и покупателей формируют все возможные рыночные ситуации (табл. 5.2).

Таблица 5.2

Типы рыночных ситуаций

Рыночные ситуации	Количество покупателей товара
Значитель­ное множест­во	Несколько десятков	В пределах шести	Один
1	2	3	4
Количество продавцов товара	Значительное множество	1	1―1	1―2	1―3	1―4
Несколько десятков	2	2―1	2―2	2―3	2―4
В пределах шести	3	3―1	3―2	3―3	3―4
Один	4	4―1	4―2	4―3	4-4

Как следует из таблицы, всего возможны 16 типовых рыноч­ных ситуаций. И для каждой из них можно глубоко проработать теорию и практику поведения фирмы, детализировать систему управления ею с тактических и стратегических позиций. Разуме­ется, это дело конкретных фирм. Такую работу многие из них выполняют, разрабатывая заранее все возможные сценарии воз­никающих на рынке ситуаций, а также заранее планируя дея­тельность фирмы, если развитие рыночных событий пойдет по одному из подобных сценариев.

Таким образом, понимание процессов всего многообразия рыночных ситуаций имеет большое практическое значение для деятельности конкретных фирм. Однако с позиций теории такое многообразие является излишним. Его можно упростить за счет замены четырех типов покупателей одним абстрактным сово­купным покупателем.

Пример. Имеется некоторая фирма, выступающая на рынке и как покупатель, и как продавец. Фирма покупает сырье, мате­риалы, топливо, энергию, комплектующие изделия, оборудова­ние, рабочую силу, финансовые ресурсы. Все приобретенные ресурсы формируют издержки фирмы, которые в зависимости in количества покупателей одного и того же ресурса будут меньше или больше. Следовательно, через издержки производства опосредованно будет учитываться рыночная ситуация со стороны покупателя ресурсов.

Учитывая эти издержки, принимая их за некоторую дан­ность, за постоянно действующий параметр производства, мож­но условно свести все многообразие покупательского рынка к одному абстрактному покупателю, которому и будут присущи именно те цены на ресурсы, по которым их будет покупать дей­ствующая на рынке фирма.

Итак, сформировав издержки производства и зная законо­мерность их изменений, можно обратить внимание на фирму как на продавца товара. Вот здесь и возникает ключевая для фирмы задача. Нужно знать, сколько товара надо произвести, и по какой цене его продать, чтобы достичь определенной цели. В качестве таковой может выступать максимум прибыли или максимум вы­ручки (в исключительных случаях фирма может изменить крите­рий принятия своего управленческого решения).

Сколько производить товара, и по какой цене его продавать — зависит от количества продавцов данного товара, от то­го, какая конкуренция существует между ними. Следовательно, выделенные четыре типа рыночных ситуаций продавцов товара будут по сути дела в теоретическом плане отражать четыре ры­ночные модели. Их характерные особенности и признаки пред­ставлены в табл. 5.3.

Таблица 5.3                      

Характерные черты моделей рынка

 

Характерная черта	МОДЕЛЬ РЫНКА
Чистая кон­куренция	Монополистиче­ская конкурен­ция	Олигополия	Чистая монополия
1	2	3	4	5
Число фирм	Значительное	Несколько де­сятков	Несколько	Одна
Тип продукта	Стандартизи­рованный	Дифференциро­ванный	Сложная стандарт­ная  или дифференцированная	Уникально сложная. Нет заменителей
Контроль над ценой	Отсутствует	В узком диапа­зоне	Ограниченный вза­имной зависимо­стью. Значительный при тайном сговоре	Значительный
Условия всту­пления в от­расль	Очень лег­кие, препят­ствия отсут­ствуют	Сравнительно легкие	Существенные пре­пятствия	Блокировано
Неценовая конкуренция	Качество	Качество, ас­сортимент	Качество, ассорти­мент, сервис	Отсутствует
Примеры	Продукты сельского хо­зяйства	Сигареты, кон­феты, одежда, обувь	Электробытовая техника, сталь, ав­томобили, тракторы	Гидротурбины, электровозы, атомные реакторы, па­ровые котлы

Чистая конкуренция и чистая монополия в практике рынка встречаются довольно часто. Однако наибольший удельный вес в   рыночной   действительности   занимают   монополистическая конкуренция и олигополия, т.е. такие модели, которые принято относить к несовершенной конкуренции.

5.5. Совокупный спрос и совокупное предложение товаров

В каждый данный период, при каждом уровне общественного развития существует вполне определенная потребность в конкретном товаре. Естественно, спрос на этот товар со стороны общества в зависимости от действия ценового и неценовых факторов может только в частном случае при весьма благоприятных обстоятельствах (низкая цена на товар, высокие доходы потребителей и т.п.) совпадать с потребностью. Во всех остальных случаях спрос, как правило, несколько ниже потребности и составляет определенную ее долю. В зависимости от конъюнктуры рынка и вида конкуренции эта доля может либо возрас­тать, либо снижаться. Товарная масса, приобретаемая на рынке, отражает так называемый совокупный спрос на данный товар. Спрос формируется под влиянием суммарного спроса всех по­купателей. Последний зависит от цены на данный товар и вели­чины всех прочих неценовых факторов. Сама цена (при прочих равных условиях) в точке равновесия целиком зависит от пред­ложения данного товара на рынке. Спрос и предложение товара в этом случае уравновесятся.

Таким образом, в зависимости от величины предложения товара и соответствующего ему спроса устанавливается определенная цена на товар. Если предложений окажется больше, то это приведет к снижению цены, и равновесие между спросом и предложе­нием вновь установится. Если предложение уменьшится, то цена возрастет, а спрос сократится, уравновесив предложение товара.

Говоря о предложении товара, необходимо понимать, что оно  представляет собой сумму всей товарной массы одинакового назначения, поставляемой на рынок всеми конкурентными фирмами, т.е. предложение является совокупным.

Возникает вопрос: как изменится совокупное предложение товара, если одна из конкурентных фирм изменит объемы производства и поставок на рынок этого товара? Как при этом из­менится цена товара на рынке? Что произойдет, если и конку­ренты введут свои поправки в производственную программу данного товара?

Попытаемся ответить на эти вопросы, для чего примем сле­дующие обозначения.

Совокупное предложение всех фирм в базовом периоде В_б. Предложения конкретной конкурентной фирмы  в базовом периоде В_ф. Доля фирмы в совокупном предложении в базовом периоде U_{ф .}

                                                                         (5.15)

Тогда совокупное предложение в принятых обозначениях со­ставит:

В_б = (В_б – В_ф) + В_{ф .}

Определяем доли в совокупном предложении всех конку­рентных фирм. Для этого левую и правую части полученного выражения разделим на В_б :

 

Введем дополнительную информацию о поведении конкурентной фирмы и всех прочих фирм в новом анализируемом периоде.

Пусть а — коэффициент изменения предложения всех про­чих конкурентных фирм в анализируемом периоде по сравне­нию с базовым (если а = 1, то совокупное предложение всех прочих форм не меняется; если а > 1, то предложение растет; если а < 1, то предложение снижается);

b — коэффициент изменения предложения конкурентной фирмы в анализируемом периоде по сравнению с базовым (если b = 1, то предложение фирмы не меняется; если b > 1, то предложение фирмы растет; если b < 1, то предложение фирмы сокращается), который по смыслу аналогичен такому же коэффи­циенту из параметрических моделей типа 4.5 и 4.6. Тогда сово­купное предложение всех фирм, вместе взятых, в анализируе­мом периоде по сравнению с базовым составит:

             

                          (5.16)

Если b_с = 1, то, значит, в анализируемом периоде совокуп­ное предложение товара на рынке как результат действия всех фирм останется на уровне базового предложения. При b_с  ≠ 1 со­вокупное предложение изменится: оно будет либо больше базо­вого (при b_с  > 1), либо меньше (при b_с  < 1).

Формула 5.16 позволяет определить совокупное предложение товара для случая, когда конкурентная фирма действовала на рынке в базовом периоде и остается в нем в новом анализируе­мом периоде. Однако очень часто возникает проблема оценки совокупного предложения товара, когда конкурентная фирма, не производя данного товара в базовом периоде, решила войти в отрасль, т.е. освоить производство и выпускать товар в анализируемом периоде.

При таком варианте изменение совокупного предложения товара на рынке можно представить в виде следующей формулы:

                                    В_с = В_б • а + B_фа,

где В_с  — совокупное предложение всех фирм в анализируемом периоде, в абсолютном выражении;

B_фа  — предложение конкурентной фирмы в анализируемом периоде, в абсолютном выражении.

Определим доли всех конкурентных фирм в анализируемой периоде в совокупном их предложении. Для этого разделим лев и правую часть этого выражения на величину В_б . Тогда получим:

                     ( 5.17)

где а_ф —доля конкурентной фирмы, входящей в отрасль анализируемом периоде, по отношению к величине базового со­вокупного предложения.

Полученное выражение свидетельствует о том, что совокуп­ное предложение всех конкурентных фирм в анализируемом пе­риоде зависит от того, как изменится это предложение по срав­нению с базовым периодом (будет ли коэффициент  а > 1, а = 1, или а < 1) и какую долю к этой величине добавит фирма, входящая в отрасль.

Если а + а_ф = 1, то совокупное предложение в анализируе­мом периоде останется по сравнению с базовым неизменным (например, а = 0,9 и а_ф = 0,1). Если сумма этих коэффициен­тов окажется меньше или больше единицы, то совокупное предложение всех конкурентных фирм в анализируемом периоде со­ответственно либо сократится, либо увеличится по сравнению с базовым периодом.

5.6. Изменение производства товара при разных моделях рынка

На рынке сталкиваются интересы всех конкурентных фирм, и от того, какую экономическую политику будет проводить каж­дая из них, ситуация для конкретной фирмы может складывать­ся вполне удачно или, наоборот, крайне неблагоприятно. Мно­гое здесь зависит от рыночной модели, в которой действует конкретная конкурентная фирма, а также от того, может ли фирма каким-то образом влиять на эту ситуацию, изменить ее в нужном для себя направлении.

Рассмотрим действия конкретной фирмы в определенной рыночной ситуации. Начнем с совершенно конкурентного рын­ка, т.е. с рынка чистой конкуренции, где доля конкурентной фирмы в общем объеме совокупного предложения крайне мала. Предположим, что фирма увеличивает объем производства това­ра, скажем, в два-три раза, и посмотрим, как изменится сово­купное предложение на рынке. Расчет выполняем по формуле 5.16. Дополнительно примем U_ф = 0,001, т.е. доля конкурентной фирмы на рынке составляет одну тысячную часть совокупного предложения. Тогда в зависимости от значений параметров а и b величина совокупного предложения в анализируемом периоде составит следующие значения (табл. 5.4):

Таблица 5.4

Величина совокупного предложения b_с  при чистой конкуренции

Коэффициент изменения предложения фирмы, b	Коэффициент изменения предложения всех конкурентных фирм,      а
0,75	1,0	1,5
0,8	0,75	1,0	1,5
1,0	0,75	1,0	1,5
1,25	0,75	1,0	1,5
1,5	0,75	1,0	1,5
1,75	0,75	1,0	1,5
2,0	0,75	1,0	1,5

Как вытекает из данных, представленных в таблице, величина коэффициента b, т.е. деятельность конкурентной фирмы, практи­чески не оказывает влияния на величину совокупного предложения в анализируемом периоде. На совокупное положение воздей­ствует только совокупное действие всех остальных конкурентных фирм, которое проявляется в значении коэффициента   а.

Действительно, если воспользоваться формулой 5.15 и при­нять удельный вес конкурентной фирмы в базовом периоде U_ф = 0 (что практически соответствует действительности), то окажется, что  b_с =  а. Это и подтверждается расчетом, результаты которого представлены в табл. 5.4. Но поскольку рыночная цена товара формируется под влиянием совокупного предложе­ния всех фирм, действующих на рынке, одна конкурирующая фирма при чистой конкуренции повлиять на эту цену не может. Она может и должна приспосабливаться к этой цене, держать ее в качестве ориентира при выработке планово-управленческого решения об объеме производства товара.

Особенно благоприятной для конкурентной фирмы является ситуация, когда все остальные фирмы снижают совокупную по­ставку товаров на рынок (т.е. при а < 1), или в крайнем случае сохраняют ее на уровне базового периода. Это должно привести к росту цены товара. Если конкурентная фирма при такой ситуа­ции повысит объем производства товара, то ее выигрыш будет весьма ощутимым. Он выразится в резком увеличении прибыли фирмы благодаря трем обстоятельствам: росту цены товара, сни­жению издержек производства и увеличению объема изготовления и поставки на рынок готового товара.

Ситуация для конкурентной фирмы может существенно ос­ложниться, если объем производства и поставки на рынок това­ра остальными фирмами несколько возрастет (т.е. при а > 1). Тогда цена товара упадет, и фирме надо будет принимать труд­ное решение: увеличивать производство своего товара, сохранять его на прежнем уровне, сокращать производство или во­обще прекратить его, выйдя из отрасли. Найти верное решение можно лишь на основании конкретных расчетов прибыли кон­курентной фирмы при разных объемах производства продукции. Незаменимую помощь при этом может принести компьютериза­ция расчетов и получение многовариантной информации по всему массиву возможных объемов производства продукции.

Следует также отметить, что все ситуации, которые могут возникнуть на рынке чистой конкуренции, происходят спонтан­но и практически не управляемы со стороны конкурентных фирм. Объясняется это тем, что действующих на рынке фирм очень много, что делает сговор между ними для оказания влия­ния на ситуацию на рынке практически нереальным.

Мало что может измениться и в случае монополистической конкуренции. Проверим это утверждение путем расчета сово­купного предложения всех конкурентных фирм по формуле 5.16, дополнительно приняв U_ф = 0,05. Это значит, что на рынке одновременно действует примерно 20 фирм. Исходное условие в этом случае предполагает, что конкурентная фирма в базовом Периоде имела рыночную долю 5%, а доля всех других фирм со­ставляла 95%.

Тогда в зависимости от значений параметров а и b, величина совокупного предложения в анализируемом периоде составит следующие значения (табл. 5.5):

Полученные результаты свидетельствуют о том, что монополистическая конкуренция по свои рыночным последствиям для конкурентной фирмы мало чем отличается от совершенной конкуренции. Действительно, если конкурентная фирма увели­чит объем производства продукции даже в два раза (т.е. изме­нится с 1,0 до 2,0), то это увеличит совокупное предложение товара на рынке всего лишь на 4―6%. Поэтому все основные выводы для чистой конкуренции свойственны и монополистиче­ской конкуренции.

Таблица 5.5

Величина совокупного предложения b_с

при монополистической конкуренции

Коэффициент изменения предложения фирмы, b	Коэффициент изменения предложения всех конкурентных фирм,    а
0,75	1,0	1,5
0,8	0,7525	0,9	1,465
1,0	0,7625	1,0	1,475
1,25	0,775	1,0125	1,4875
1,50	0,7875	1,025	1,50
1,75	0,8	1,0375	1,5125
2,0	0,8125	1,05	1,525

Проанализируем рыночную ситуацию при олигополии. Примем рыночную долю фирмы в базовом периоде U_ф = 0,25, т.е. допустим, что на рынке одновременно действуют четыре фирмы.

Тогда в зависимости от значений параметров а и b величина совокупного предложения в анализируемом периоде составит следующее значение (табл. 5.6).

Таблица 5.6

 

Величина совокупного предложения b_с

при олигополии

Коэффициент изменения предложения фирмы,   b	Коэффициент изменения предложения всех конкурентных фирм, а
0,75	1,0	1,5
0,8	0,762	0,95	1,32
1,0	0,812	1,0	1,375
1,25	0,875	1,062	1 ,487
1,50	0,934	1,125	1,5
1,75	1,0	1,187	1,562
2,0	1,062	1,25	1,625

Цифры, представленные в таблице, говорят о том, что в ус­ловиях олигополии даже одна фирма может существенно влиять на величину совокупного предложения, а следовательно, воз­действовать на рыночную цену товара. Так, при увеличении объема производства конкурентной фирмой вдвое совокупное предложение (при прочих равных условиях) может возрасти с 18 до 30%. Эти величины значительно могут повлиять на цену то­вара. Таким образом, даже одна фирма своим поведением на рынке может серьезно воспрепятствовать проникновению в от­расль других фирм.

Однако, разумеется, самое сильное влияние на рыночные отношения может оказать фирма-монополист, т.е. фирма, функционирующая в условиях чистой монополии. Рыночная доля такой фирмы в базовом периоде составляет U_ф = 1,0. При таких исходных данных расчет совокупного предложения в ана­лизируемом периоде по формуле 5.16 дает следующие результа­ты (табл. 5.7).

Таблица 5.7

Величина совокупного предложения b_с при чистой монополии

Коэффициент изменения предложения фирмы, b	Коэффициент изменения предложения всех конкурентных фирм,   а
0,75	1,0	1,5
0,8	0,8	0,8	0,8
1,0	1,0	1,0	1,0
1,25	1,25	1,25	1,75
1,50	0,50	1,50	1,50
1,75	1,75	1,75	1,75
2,0	2,0	2,0	2,0

Здесь полученные результаты совокупного предложения полностью зависят от изменения поведения монополистиче­ской фирмы — от величины коэффициента b, а это результа­ты прямо противоположные чистой конкуренции, где сово­купное предложение практически полностью зависит от пове­дения всех конкурентных фирм вместе взятых, т.е. от значе­ния коэффициента   а.

При таких условиях монополистическая фирма практически безраздельно господствует на рынке, проводя нужную ей ценовую политику, формируя выгодное для себя предложение това­ра. Проникнуть в отрасль со своим товаром для любой фирмы весьма затруднительно, а иногда — просто невозможно, ибо фирма-монополист может всегда наводнить рынок своим това­ром, резко снизив цену на него, и тем самым поставить фирму-конкурента на грань катастрофы.

Как следует из проведенного анализа, для рыночного поло­жения каждой конкурентной фирмы огромную роль играет по­казатель доли фирмы в совокупном предложении, т.е. U_ф. Дан­ный показатель, определяемый по формуле 5.15, по сути дела отражает уровень монополизации рынка данной конкурентной фирмы. И чем выше этот уровень, тем увереннее может чувст­вовать себя конкурентная фирма на рынке.

Рассмотрим некоторые частные случаи, вытекающие из формулы 5.15.

1. Показатель U_ф = 0, т.е. имеется совершенно конкурент­ный рынок. Тогда совокупное предложение в анализируемом периоде b_с = а.

Это значит, что положение каждой конкурентной фирмы на рынке всецело зависит от их совместно-результирующего пове­дения. Сократят они производство товаров — цены возрастут, увеличат производство — цены товаров снизятся. Отсюда и по­ложение конкретной фирмы: оно будет неуверенным, неста­бильным, неуправляемым, ибо устойчивость и надежность кон­курентной фирмы в этом случае будет целиком зависеть от ры­ночной стихии.

Разумеется, и при чистой конкуренции фирме могут быть даны рекомендации, направленные на безусловное обеспечение ее выживаемости. Это, конечно, корректировка своего поведе­ния, связанная с постоянным совершенствованием выпускаемой продукции, повышением ее качества, внедрением достижений научно-технического прогресса в производство, обеспечивающим снижение издержек, и, наконец, постоянное регулирование, объема производства продукции в соответствии с конъюнктурой, рынка.

2.  Показатель  U_ф = 1, т.е. рассматривается рынок чистой монополии, где фирма — единственный производитель данного товара. Совокупное предложение фирмы-монополиста составля­ет b_с = b.

Такая фирма всецело контролирует рынок и может, когда ей понадобится, сокращать производство товара или увеличивать его. При этом ценовая политика фирмы целиком определяется ее собственными интересами. Положение фирмы на рынке, как правило, стабильное, устойчивое, надежное. Оно контролирует­ся фирмой и управляемо ею.

3. Этот случай характерен тем, что а = b, т.е. конкурентная фирма ведет себя так, как ведут себя в совокупности все другие действующие на рынке фирмы, т.е. сокращает или увеличивает производство товара. Такое поведение очень логично, ибо все фирмы учитывают в своем поведении действие одних и тех же факторов и одинаково оценивают ситуацию на рынке.

В результате такого поведения фирм независимо от модели рынка (чистая конкуренция, монополистическая конкуренция, олигополия или монополия) совокупное предложение товара будет определяться выражением b_c = b или b_с = а. Конкурент­ная фирма вынуждена подчиняться  действию рыночной тенден­ции, подстраиваться под общий рыночный режим, выйти из ко­торого можно, но при этом риск значителен. Во всяком случае некоторые фирмы не без успеха применяют нестандартные пла­ново-управленческие решения, связанные с изменением объема; производства продукции, ее качества, освоением новинок и т.п.

Вхождение в отрасль. Фирма, которая стремится войти в отрасль, должна четко представлять, с какими трудностями ей; предстоит столкнуться, в какой рынок она желает войти и како­вы наиболее благоприятные условия вхождения в отрасль.

Чтобы ответить на эти вопросы, следует обратиться к формуле 5.17, анализ которой позволит с достаточной достоверно­стью дать фирме необходимые рекомендации.

Воспроизведем эту формулу:

                                    (5.17)

Самая простая и общая рекомендация, которая может быть дана фирме независимо от модели рынка — входить в отрасль в наиболее благоприятный для нее момент.

Такой момент наступает, когда объем производства товара, а следовательно, совокупное предложение товара всеми конку­рентными фирмами сокращается (т.е. а < 1), а цена на него возрастает. В этот период вхождение в отрасль для любой фир­мы связано с минимальным риском. Высокая цена на товар дает ей надежное прикрытие и позволяет освоиться на рынке, адап­тироваться к изменяющимся условиям, менее болезненно реализовывать свои усилия по освоению производства нового для фирмы товара.

Однако следует быть очень осторожным при попытке вхожде­ния в отрасль в условиях олигополистического и особенно моно­полистического рынка, когда одна-две конкурентные фирмы могут довольно быстро перестроиться и изменить ситуацию на рынке. Тогда благоприятный момент вхождения в отрасль может обернуться для фирмы сокрушительной катастрофой: цена на товар резко упадет, разорение фирмы окажется неизбежным.

5.7. Оптимизация планово-управленческого

        решения деятельности предприятия

Большой интерес для любого предприятия, работающего в условиях цивилизованного рынка, представляет вопрос приня­тия оптимального планово-управленческого решения, создаю­щего ему при прочих равных условиях лучшие хозяйственные и экономические возможности благоприятной работы по сравне­нию с альтернативными вариантами. Однако это не означает, что подобное решение автоматически обеспечит предприятию безубыточность производства и устойчивое его положение на рынке, надежную и стабильную работу, экономическую безо­пасность. Просто такое решение будет лучшим для предприятия в условиях сложившихся рыночной конъюнктуры и затрат на производство, сформировавшихся цен на товары и т.п.

Информация о рыночных и производственных параметрах деятельности предприятия, реализующего оптимальное планово-управленческое решение, очень важна для высших менеджеров, формирующих политику фирмы, ее стратегию развития и такти­ку реализации. Пусть даже оптимальное решение не очень бла­гоприятно для фирмы, но оно все же дает ей чрезвычайно важ­ную информацию о том, как и за счет чего можно исправить трудное положение, как нужно управлять деятельностью, чтобы выйти из сложной ситуации и больше в нее не попадать. Во всяком случае знания о лучшем решении и его реализация позволяют избежать значительно худшего для фирмы положения, и в этом своем качестве оно будет очень полезным для предпри­ятия, откроет для него потенциальные резервы улучшения дея­тельности в будущем.

Надо отметить, что оптимизация планово-управленческого решения не может быть получена на пустом месте. Для этого нужна богатая информация, которую службам маркетинга пред­приятия необходимо постоянно собирать, накапливать, регуляр­но обновлять, перерабатывать, формировать ее на таком уровне, на каком она может быть использована с наибольшей пользой для предприятия.

В данном случае речь идет об информации:

• о произведенном и поставляемом на рынок готовом про­дукте, об аналогичных товарах-конкурентах;

• о затратах на производство продукции, об их структуре;

• касающейся сложившихся на рынке цен на товары, дохо­дов потребителей, товаров взаимозаменяемых и взаимодопол­няемых;

• относящейся к объемам производства конкурирующих фирм, к их ценовой и структурной политике, прогнозам их по­ведения в будущем.

Вместе с тем кроме этих знаний фирма должна выбрать для себя критерий оптимизации планово-управленческого решения. Важнейшим критерием в условиях рыночной экономики, безусловно, является прибыль предприятия, ибо именно она есть цель рыночного хозяйствования.

Разумеется, максимизация прибыли как критерия оптимизации деятельности предприятия является предпочтительной в условиях нормальной, стабильной экономики. Однако рынку присущи разные ситуации. При отклонениях от нормальной экономики цели и задачи предприятия могут существенно меняться, что выражается в изменении экономической политики предприятия. Чтобы новую политику отразить в плане, необходимо из­менить и критерий оптимизации управленческих решений.

В качестве альтернативного критерия, который при опреде­ленных условиях может оказаться лучше других, можно предло­жить, например, критерий максимума выручки от реализации товарной продукции и другие специфические критерии.

Выбор планово-управленческого решения по критерию максимума прибыли предприятия. Максимизация прибыли предпри­ятия — наиболее распространенный критерий выбора планово-управленческого решения. Его предпочитают предприятия, ра­ботающие в стабильной экономике, сами функционирующие стабильно и стремящиеся к постоянному развитию. В основе оптимизации деятельности предприятия по максимуму прибыли нежит построение такой многопараметрической модели, в кото­рой будет установлено наиболее предпочтительное соотношение между ценой продажи товара и объемом производства и реализации его на рынке. Причем надо учитывать, что цена товара на рынке складывается под влиянием совокупного спроса и предложения, а объем производства и реализации конкретного това­ра рассматривается и учитывается по вполне определенному предприятию — одному из некоторого числа конкурентов.

Построение математической модели для определения сово­купного спроса товара на рынке начнем с формулы 5.12:

Но коль скоро рассматривается рыночное равновесие, мож­но записать и использовать для искомой модели формулу сово­купного предложения товара 5.16:

Поскольку левые части выражений 5.12 и 5.16 равны между собой, то можно приравнять друг к другу их правые части, а за­тем из полученного равенства определить цену товара на рынке:

             

               (5.18)

Чтобы определить цену товара на рынке, надо знать сле­дующие параметры:

• коэффициент эластичности спроса товара от цены на него (K_эц)

• совокупное числовое значение действия всех неценовых факторов (формула 5.13);

• цену товара в базисном периоде;

• прогноз изменения поставок товаров на рынок всеми кон­курентами данной фирмы в анализируемом периоде а;

• планируемую поставку товара на рынок данным предпри­ятием в анализируемом периоде b.

Всю информацию, представленную в формуле 5.18, можно разделить на три части. Первая часть — информация, которая должна быть известна из прошлого периода. Как правило, она довольно стабильна и остается неизменной на данном сегменте рынка длительное время. Такая информация включает все коэффициенты эластичности спроса товара (ценовая, по доходу потребителя,  перекрестная эластичность,  по качеству продукции). Сюда же можно отнести информацию о рыночной доле предприятия по конкретному товару.

Вторая часть информации относится к прогнозируемой величине. Ее нужно стараться предвидеть как можно точнее. Это прогноз об  изменении доходов потребителей, об изменениях цен на взаимозаменяемую продукцию, об изменениях качества рыночной продукции в анализируемом периоде, об изменениях в объеме товарной массы, которую поставляют конкуренты дан­ного предприятия.

И наконец, третья часть информации — объем производства и поставок на рынок данным предприятием товара в анализируемом периоде. Такая информация всецело зависит от са­мого предприятия, пытающегося оптимизировать свою прибыль.

Очевидно, что по мере изменения объема производства реализации продукции общее количество товарной массы на рынке также будет изменяться, а следовательно, изменится цена на товар в анализируемом периоде, подсчитать которую можно по формуле 5.18.

Итак, зная планируемый объем производства и реализации товара конкретным предприятием и определяя соответствующую  ему цену товара по формуле 5.18, можно подставить полученную информацию в формулу типа 4.5 или 4.6 и определить прибыль предприятия.

Решение, при котором достигается максимум прибыли, можно найти двумя методами.

Первый метод — пошаговый дискретный расчет прибыли с использованием заранее подготовленной информации для разных объемов производства и реализации продукции. Рассмотрим этот метод на конкретном примере.

Для определения цены товара примем следующие данные для расчета: К_эц = 0,8;  К_эд = 1,0;  Д = 1,1;  d_в = 1,0; d_с = 1,0;   I_к = 1;   U_ф = 0,4;  а  = 1,2.

На основе этих исходных данных можно сказать, что здесь присутствуют благоприятные и неблагоприятные для предприятия факторы. Благоприятным можно считать фактор по­вышения дохода потребителей товара на 10% (Д = 1,1), по­скольку действие его должно привести к повышению спроса на товары или к росту цены на него. Неблагоприятным фактором является прогноз о повышении поставки на рынок всеми конкурентами товарной массы на 20% (а = 1,2), что приведет к снижению цены товара. Посмотрим, как это отразится на поло­жении нашего предприятия. Предположим, что, учитывая увеличение дохода потребителей и рост поставок товаров конку­рентами, предприятие тоже запланирует прирост выпуска про­дукции, скажем на 5% (т.е. b = 1,05).

Подставив исходные данные в формулу 5.18, получим:

Итак, при запланированном увеличении объема производст­ва товара на 5% общее количество товарной массы значительно возрастет, что приведет к снижению равновесной цены товара па рынке тоже на 5% (d = 0,95).

Посмотрим, как это отразится на прибыли. Рассчитаем ее по модели типа 4.5. Для определения индекса прибыли примем:

 р = 1,15;   К_н = 1,0   r = 0,6;    f = 0,0. Тогда будем иметь:

Итак, получен результат, который свидетельствует, что для нашего предприятия ситуация на рынке складывается весьма неблагоприятно: индекс прибыли снизится до 0,781, а сама при­быль сократится по сравнению с базовым периодом на 28%.

Вместе с тем отметим, что предприятие может изменить объ­ем производства и поставок товаров на рынок. Следовательно, при прочих принятых для расчетов параметрах можно принять такой алгоритм поиска оптимального решения.

Первый шаг. Принять для начала расчета какой-то реальный объем производства и поставок на рынок товара, т.е. принять величину b. Для этого объема определить по формуле 5.18 цену товара, как сделано по рассмотренному периоду. Зная объем по­ставок товара и его цену, можно определить индекс прибыли по модели типа 4.5 или 4.6.

Второй шаг. Уменьшим по сравнению с первым шагом объ­ем планируемых поставок товара на 0,01. Весь расчет повторим (т.е. определим цену, а затем — индекс прибыли).

Третий шаг. Увеличим по сравнению с первым шагом объем  планируемых поставок товара на 0,01. Весь расчет повторим.

Четвертый шаг. Определим направление: изменения индекса прибыли с уменьшением и увеличением объема производств поставок товара, а также объем, при котором прибыль растет. В этом направлении и следует вести поиск лучшего решения, меняя в каждом решении объем поставок товара на 0,01.

Пятый шаг. Определим, при каком объеме поставок товара наступает максимум прибыли. Это решение и будет оптимальным.

Подтвердим справедливость такого алгоритма, продолжив решение начатого примера. Результаты расчета представлены в рабочей таблице.

№ п/п	Объем производства	Цена товара	Индекс прибыли	№ п/п	Объем производства	Цена Товара	Индекс прибыли
b	d	I	b	d	I
1	1,05	0,95	0,781	12	0,94	1,005	0,816
2	1,04	0,955	0,788	13	0,93	1,01	0,814
3	1,03	0,96	0,794	14	0,92	1,015	0,812
4	1,02	0,965	0,8	15	0,91	1,02	0,809
5	1,01	0,97	0,804	16	0,90	1,025	0,806
6	1,0	0,975	0,808	17	0,89	1,03	0,801
7	0,99	0,98	0,812	18	0,88	1,035	0,796
8	0,98	0,985	0,814	19	0,87	1,04	0,79
9	0,97	0,99	0,816	20	0,86	1,045	0,783
10	0,96	0,995	0,816	21	0,85	1,05	0,775
11	0,95	1,00	0,817	22	0,84	1,055	0,767

Как показывают данные, максимум прибыли достигается при снижении объема производства и поставок товаров до b = 0,95 (т.е. снижение на 5%). Тогда цена товара в сравнении с базовым периодом не изменится (d = 1,0), а прибыль в этих ус­ловиях будет самой большой. Ее индекс составит I = 0,817. Это значит, что даже самый лучший результат деятельности пред­приятия окажется хуже результата базового периода.

Второй метод нахождения оптимального решения заключа­ется в том, чтобы выразить индекс прибыли в виде функции, которая будет зависеть от всех действующих параметров. Если затем взять первую производную этой функции и приравнять ее к нулю, то, разрешив полученное уравнение относительно неиз­вестного, можно определить оптимальную цену товара. Ей будет соответствовать оптимальный объем производства и поставок товара на рынок. По полученным оптимальным значениям цены и объема продаж легко определяется индекс прибыли.

Для реализации этого метода выразим объем производства и поставок товара по формуле

                          (5.19)

Полученное выражение подставим в формулу индекса при­были типа 4.5 вместо параметра объема производства продукции и возьмем первую производную относительно цены товара. Приравняв ее затем к нулю, определим величину оптимальной цены товара:

                   (5.20)

После этого определим оптимальный объем производства по формуле

                           (5.21)

И наконец, определим оптимальный индекс прибыли:

                     (5.22)

Рассчитаем оптимальные параметры цены, объема произ­водства товаров и оптимальный индекс прибыли предприятия для рассматриваемого примера.

Оптимальная цена товара:

Оптимальный объем производства:

Оптимальный индекс прибыли:

Таким образом, получен результат, который практически точно совпадает с одиннадцатой строчкой пошагового решения. То есть сразу же, без многочисленных расчетов получен искомый результат оптимального планово-управленческого решения при данных фиксированных условиях, отражающих рыночную ситуацию и производственные параметры затрат предприятия.

Выбор метода оптимизации остается за фирмой и определяется стоящими перед ней задачами. Отметим лишь, что первый из рассмотренных методов при всей своей трудоемкости дает возможность получить богатую информацию о зависимости ин­декса прибыли от установленного объема производства, а вто­рой метод позволяет найти готовое оптимальное решение кратчайшим путем.

Выбор планово-управленческого решения по критерию максимума выручки предприятия. В отдельных случаях, а именно когда предприятие испытывает острую нужду в денежных средствах, выбор планово-управленческого решения может быть произведен по критерию максимизации выручки. В основе такого решения лежат те же мотивы, что и при выборе в качестве критерия максимума прибыли, а кроме того, здесь может быть при­менен один из двух рассмотренных методов оптимизации.

Для начала поиска лучшего решения по указанному крите­рию необходимо построить многопараметрическую модель зави­симости индекса выручки предприятия от влияющих на нее всех рыночных факторов. В общем виде такая зависимость может быть представлена в виде следующего выражения:

                               I_в  = b · d,                                 (5.23)

Где I_в   — индекс выручки предприятия, отражающий измене­ние абсолютной выручки в анализируемом периоде по сравне­нию с базовым;

b  — коэффициент изменения объема производства и реа­лизации  продукции в анализируемом и базовом периодах, кото­рый для целей оптимизации принимается по формуле 5.19;

d — коэффициент изменения цены товара в тех же пе­риодах, учитывающий конъюнктуру рынка и все действующие факторы, обеспечивающий равновесие спроса и предложения товара (формула 5.18).

Подставим в формулу 5.23 вместо коэффициента b равное ему выражение из формулы 5.19. Тогда получим:

                       (5.24)

Возьмем первую производную полученного выражения, при­равняем ее к нулю, а затем из записанного равенства определим оптимальную цену товара (т.е. воспользуемся вторым методом).

После необходимых преобразований полученного выражения получим:

                                            (5.25)

Оптимальной цене будет соответствовать оптимальный объ­ем производства и реализации продукции. Его можно опреде­лить по формуле

                 (5.26)

И, наконец, оптимальная выручка будет равна

           (5.27)

 По выведенным формулам произведен расчет оптимальной выручки для фиксированного выше примера:

Воспользуемся первым методом оптимизации. Для этого за­дается объем производства и реализации продукции и определя­ется соответствующая ему цена товара по формуле

             (5.28)

Затем полученные значения объема производства b и цены товара d подставляются в формулу 5.23, в результате чего полу­чается выручка  предприятия. Просчитав ее для разных значений объема производства и цены товара, можно получить законо­мерность изменения индекса выручки предприятия. Из полу­ченной закономерности определяется максимум выручки. Рас­считаем индекс выручки для разных сочетаний объема производства и цены товара и покажем результаты в следующей рабо­чей таблице.

№ п/п	Объем про­изводства, b	Цена товара, d	Индекс вы­ручки, В	№ п/п	Объем производства, b	Цена товара, d	Индекс выручки, В
1	1,6	0,675	1,08	5	1,3	0,825	1,0725
2	1,5	0,725	1,0875	6	1,2	0,875	1,05
3	1,475	0,7375	1,0878	7	1,1	0,925	1,0175
4	1,4	0,775	1,085	8	1,0	0,975	0,975

Как видно из таблицы, максимум выручки отличается при b = 1,475 и d = 0,737, т.е. соответствует результату, полученному по второму методу оптимизации.

Обращает на себя внимание тот факт, что оптимизация вы­ручки предприятия сопровождается резким снижением цены то­вара (может быть даже себе в убыток) и значительным увеличе­нием объема производства и продаж товара потребителям.

Выбор планово-управленческого решения по критерию максимума рентабельности производства. По своей экономической су­ти этот критерий означает максимизацию покрытия выручкой затрат на производство продукции в анализируемом периоде. Особенно большое значение данный критерий приобретает в условиях инфляции.

Чтобы выразить искомый критерий, необходимо учесть изме­нения базовой рентабельности производства под влиянием изме­нения выручки и затрат в анализируемом периоде. Коэффициент рентабельности можно определить по формуле:

                      (5.29)

где p — коэффициент рентабельности производства в базо­вом периоде;

b — коэффициент изменения объема производства про­дукции в  натуральном выражении;

d — коэффициент изменения цены реализации единицы товара;

K_п ―  коэффициент изменения переменных затрат;

f — коэффициент изменения постоянных затрат.

Итак, многопараметрическая модель рентабельности произ­водства имеется.  Теперь надо оптимизировать управленческое решение. Оно может быть получено теми же двумя методами, рассмотренными ранее.

Начнем со второго метода. Для этого вначале выразим цену товара через объем производства (формула 5.28) и подставим это выражение в формулу 5.29. В результате получим

Теперь возьмем первую производную этого выражения по объему производства и приравняем ее к нулю. Это можно запи­сать так:

 

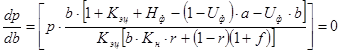
Поскольку дальнейшие преобразования полученного выра­жения выглядят очень громоздко, приведем окончательную формулу для определения оптимального объема производства и реализации продукции:

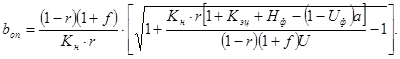           (5.30)

Затем определим соответствующую этому объему оптимальную цену товара по формуле

                                   (5.31)

Полученные значения оптимального объема производства и оптимальной цены подставим в формулу 5.29:

                                   (5.32)

По этой формуле и с использованием данных предыдущего примера найдем оптимальное планово-управленческое решение по критерию максимума рентабельности производства, опреде­лив оптимальные значения объема производства и цены товара по формулам 5.30 и 5.31.

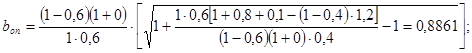
Теперь можно воспользоваться формулой 5.32, предвари­тельно приняв p = 1,15. После подстановки найденных парамет­ров получим: