|
Министерство образования РФ
Всероссийский заочный финансово-экономический институт
|
|
Кафедра
статистики
КУРСОВАЯ РАБОТА По
дисциплине «Статистика»
|
|
на тему
«Статистические методы
изучения конъюнктуры рынка»
Вариант №6
|
|
|
Исполнитель: Горчакова Елена Сергеевна Специальность:
Бухгалтерский учет, анализ и аудит
|
|
Группа: 324
№ зачетной книжки: 06убд43105 Руководитель:
Пуляшкин Владимир Васильевич
|
Содержание
|
1.Теоретическая часть
|
3
|
|
Введение
|
3
|
|
1.1.Статистические
показатели конъюнктуры
|
4
|
|
1.2. Методы исчисления
общей (абсолютной) и сравнительной (относительной) эффективности
|
6
|
|
1.3.Применение индексного метода
|
10
|
|
1.4.Применение балансового метода
|
13
|
|
Заключение
|
14
|
|
|
2.Расчетная часть
|
15
|
|
|
3.Аналитическая часть
|
|
|
|
Список
используемой литературы
|
|
|
|
|
|
1.Теоретическая часть
Введение
Экономическая статистика – это глаза и уши аналитика, это инструмент
функциональной диагностики, необходимый для принятия адекватных управленческих
и политических решений, это - зеркало, в котором отражается живой
социально-экономический организм: иногда - в целом, иногда - его отдельные
составляющие элементы. Экономическая статистика - это универсальный язык,
позволяющий общаться экономистам всех стран и всех направлений, государственным
деятелям, политикам, юристам, социологам, финансистам, менеджерам предприятий и
специалистам в области государственного управления. Именно поэтому
экономическая статистика является базовой общепрофессиональной дисциплиной для
студентов, обучающихся по всем финансовым и экономическим специальностям высших
учебных заведений.
Если брать одно из определений слова "конъюнктура", то оно
гласит, что конъюнктура - это сложившаяся на данный промежуток времени
обстановка, ситуация в какой-либо сфере общественной жизни. Если говорить об экономической конъюнктуре в условиях
капиталистической системы, то здесь имеются ввиду конкретные условия процесса
производства, а также ситуация сложившаяся на рынках на данной фазе
капиталистического цикла.
Если рассматривать сложившуюся на данный момент конъюнктуру
и определяющие ее факторы, то среди них можно выделить три основные группы:
1. Постоянно действующие факторы нециклического свойства
(научно-технический прогресс, демографические факторы, расходование природных
ресурсов).
2. Постоянно действующие циклические факторы
(экономические кризисы и подъемы).
3. Случайные и временно действующие факторы
(стихийные бедствия, войны).
Общей тенденцией мировой экономики и
большинства стран является повышение уровня цен, экономический рост - рост конъюнктуры.
Однако если даже в долговременном периоде прослеживается тенденция к росту, то
все равно рост этот не равномерен. Рост может уступать место спаду.
Данные колебания представляют собой следующие
друг за другом подъемы и спады уровней деловой активности на протяжении
некоторого периода времени. Они имеют следующие общие черты:
1. Пик цикла.
2. Спад.
3. Низшая точка.
4. Фаза оживления.
Наиболее продолжительными из выделяемых
колебаний являются так называемые "большие циклы конъюнктуры", они
имеют период 45-60 лет. На эти циклы накладываются среднесрочные колебания:
цикл запасов, среднесрочный, строительный (Кузнеца); далее следуют сезонные
колебания деловой активности. Вместе эти колебания отражают тенденции развития
экономической системы, и рыночной конъюнктуры.
1.1.Статистические показатели конъюнктуры
Рентабельность
характеризует результативность
деятельности предприятий и организаций. Показатели рентабельности используют
чтобы определить эффективность применяемых в производстве авансированных
ресурсов и текущих затрат, а также для оценки доходности и эффективности
имущества предприятия. Существует система показателей рентабельности.
Рассмотрим лишь показатели рентабельности производства и продукции.
·
Общая рентабельность производства (Р0) – отношение балансовой прибыли (Пб) к среднегодовой стоимости основных производственных
фондов и нормируемых оборотных фондов (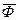 )
)
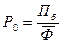 . (51)
. (51)
Характеризует прибыльность (убыточность) производственной деятельности
предприятия за определенный период времени (год, квартал)
·
Рентабельность продукции (РП) – отношение прибыли от реализации продукции (П) к сумме затрат на производство и
реализацию продукции (З):
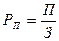 . (52)
. (52)
Характеризует эффективность использования текущих затрат живого и
прошлого труда и позволяет судить ,
какую прибыль даст каждый рубль произведенных затрат.
·
Рентабельность продаж (РПР) – отношение прибыли от реализации продукции к
объему продаж (РП)
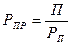 . (53)
. (53)
Показывает, какую прибыль имеет предприятие с каждого рубля реализованной
продукции. Он может быть ориентиром в оценке конкурентоспособности продукции,
так как снижение рентабельности реализованной продукции может означать и
падение спроса на нее. Рассчитывается в целом по предприятию и отдельным видам продукции.
Для того, чтобы провести сравнительную оценку эффективности производственных фондов однородных предприятий в
пределах фирмы, акционерного общества или отрасли за один и тот же год и
выяснить, какие предприятия с точки зрения обеспечения эффективности
производственных фондов являются ведущими, а какие отстающими, либо одного
предприятия, но за разные годы его работы (например, за истекшие годы отчетного
периода), насколько повысилась (или снизилась) эффективность производственных
фондов за этот период, следует пользоваться таким показателем рентабельности
предприятия
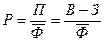 , (54)
, (54)
где П, В, З – прибыль от
реализации продукции, выручка от
реализации и затраты на производство и реализацию продукции соответственно;
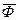 - средняя стоимость производственных фондов (основных
и нормируемых оборотных).
- средняя стоимость производственных фондов (основных
и нормируемых оборотных).
Другой способ оценки эффективности производственных фондов предприятий
основан на установлении взаимосвязи между показателями затрат на 1 рубль
продукции, фондоотдачи и показателем рентабельности предприятия
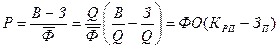 , (55)
, (55)
где Q – выпуск
произведенной продукции;
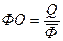 - фондоотдача,
или степень интенсивного использования производственных фондов;
- фондоотдача,
или степень интенсивного использования производственных фондов;
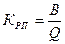 - коэффициент
реализации произведенной продукции (доля реализации);
- коэффициент
реализации произведенной продукции (доля реализации);
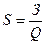 – затраты
на 1 рубль продукции.
– затраты
на 1 рубль продукции.
Третий способ оценки состоит в установлении взаимосвязи между показателями
производительности труда, фондовооруженности и показателем рентабельности
предприятия:
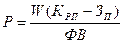 ,
(56)
,
(56)
где 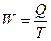 - производительность труда (выработка на 1 работника);
- производительность труда (выработка на 1 работника);
Т – среднесписочная численность
работников;
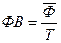 - фондовооруженность работников предприятия.
- фондовооруженность работников предприятия.
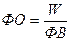 .
.
Эти способы оценки указывают на то, что все другие показатели , например
такие как затраты на 1 рубль продукции,
производительности труда, фондовооруженность, фондоотдача и др. воздействуют на
достигнутый уровень эффективности производственных фондов не обособленно и независимо
от обобщающего показателя рентабельности, а связаны с ним непосредственно
приведенными формулами (54) , (55), (56), выполняют в системе оценки свои
особые, специфические функции и служат факторами, но не средством такого рода
оценки.
Показатель рентабельности предприятия, рассчитанный как отношение прибыли
от реализации продукции к среднегодовой стоимости производственных фондов
связан практически со всеми технико-экономическими показателями предприятия
формулами (54) , (55) и (56). С помощью этих формул можно установить характер
влияния и направленность действия того или иного фактора, и создается более строгая взаимосвязанная
система экономических показателей. Без обобщающего показателя рентабельности и
его расчетных формул отчетность предприятий и организаций в части решения
проблемы повышения эффективности производства – «груда» не связанных между
собой показателей [1, 67 с.].
1.2. Методы исчисления общей
(абсолютной) и сравнительной (относительной) эффективности
Сущность проблемы повышения экономической эффективности производства
состоит в увеличении экономических результатов
на каждую единицу затрат в процессе использования имеющихся ресурсов.
Повышение эффективности производства может достигаться как за счет
экономии, текущих затрат (потребляемых ресурсов), так и путем лучшего
использования действующего капитала и новых вложений в капитал (применяемых ресурсов).
Различают абсолютную и сравнительную экономическую эффективность.
Абсолютная характеризует фактическую
эффективность уже произведенных затрат, а сравнительная вычисляется на стадиях проектирования и
планирования, когда из нескольких возможных вариантов выбирается один –
наиболее экономичный.
Сравнительная эффективность представляет
частный случай приростной эффективности (приростная эффективность
характеризуется отношением прироста эффекта за расчетный период к приросту
вызвавших их затрат), когда базой для расчета эффекта и затрат являются не
показатели прошлой деятельности, а один из сравниваемых вариантов. В качестве
эффекта здесь чаще всего выступает рост прибыли в результате снижения
себестоимости при реализации одного варианта по сравнению с другим ( или просто разность себестоимости), а в
качестве затрат – дополнительные капитальные вложения, обеспечивающие снижение
себестоимости по лучшему варианту. Сравнительная эффективность отражает лишь
эффективность совершенствования (реконструкции, развития, улучшения и т.п.)
варианта, но не эффективности функционирования усовершенствованного варианта,
последняя может оказаться и ниже нормативной.
Кроме того, сравнительная эффективность позволяет судить о преимуществах
отдельных вариантов совершенствования производства и отобрать наилучший из них,
не предопределяя конечного решения о целесообразности его реализации. Это
решение может быть принято только на основе расчета абсолютной эффективности и
сопоставления ее с нормативной.
Важнейшим экономическим результатом рыночной деятельности предприятия с
учетом долговременной перспективы его развития
является получение максимальной прибыли на вложенный капитал.
Соотношение прибыли и единовременных затрат становится исходной основой для
реального повышения эффективности производства. Отсюда в качестве исходного количественного критерия
эффективности производства должна выступать годовая норма прибыли на вложенный
каптал (Е)
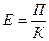 , (57)
, (57)
где К – вложения в
капитал, обеспечивающие получение
прибыли, руб.;
П – чистая прибыль (годовая) за
вычетом налогов, руб.
Расчетные значения нормы прибыли могут изменяться в зависимости от структуры
каптала, уровня прогнозируемых цен на продукцию, объема спроса и других
факторов. Выбранный критерий эффективности производства в виде нормы прибыли на
капитал применяется как для сравнения различных вариантов развития предприятия,
так и для оценки единственного варианта
рынком. В соответствии с принятым критерием определяются конкретные показатели
эффективности производства, отражающие основные характеристика затрат и
результатов.
В международной практике обоснования эффективности инвестиционных проектов
используются следующие обобщающие показатели эффективности производства: чистый
приведенный доход (чистая текущая стоимость), срок окупаемости, внутренняя
норма доходности, индекс рентабельности, рентабельность и др.
Чистая текущая стоимость (NPV) определяется как
разность между поступлением и расходом денежных средств за весь период
предполагаемого функционирования предприятия с учетом фактора времени,
представляет собой ожидаемый чистый доход, приведенный к начальному моменту
времени
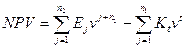 , (58)
, (58)
где 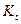 -
инвестиционные расходы в периоде t; t = 1,2,…,n2.
-
инвестиционные расходы в периоде t; t = 1,2,…,n2.
n1 - -
продолжительность процесса инвестиций;
n2 -
продолжительность периода отдачи от инвестиций;
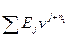 -
дисконтированная сумма денежных доходов;
-
дисконтированная сумма денежных доходов;
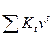 -
дисконтированная сумма денежных доходов;
-
дисконтированная сумма денежных доходов;
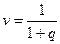 - коэффициент
приведения (дисконтирования);
- коэффициент
приведения (дисконтирования);
q - ставка сравнения .
(При ее выборе ориентируются на существующий или ожидаемый усредненный уровень
ссудного процента. Практически выбирают
конкретные ориентиры, например,
ставку банковского процента за кредитные ресурсы, доходность
определенных видов ценных бумаг и др.)
Если NPV>0 ,
то проект следует принять,
NPV<0,
то проект следует отвергнуть;
NPV=0 , то проект ни прибыльный , ни убыточный.
Предполагается, что процесс отдачи
идет сразу после окончания инвестиций.
Пример1. Имеются варианты,
характеризующиеся следующими потоками
платежей в тыс. руб. для упрощения
отнесем соответствующие показатели к концу года.
|
Годы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
А
|
-100
|
-150
|
50
|
150
|
200
|
200
|
-
|
|
В
|
-200
|
-50
|
50
|
50
|
100
|
200
|
200
|
При нормативе рентабельности
(ставке сравнения) q=
10% определить чистый приведенный доход по каждому варианту и сравнить их.
Решение.
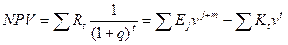
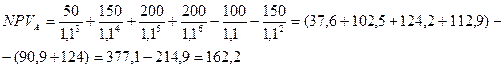
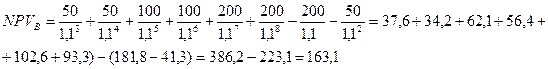
Таким образом, если исходить из величины чистой текущей стоимости, при
принятой процентной ставке сравниваемые варианты в финансовом отношении
практически равноценны.
Необходимо отметить, что показатель
NPV отражает
прогнозную оценку изменения
экономического потенциала
предприятия в случае принятия рассматриваемого проекта. Этот показатель аддитивен
во временном аспекте, т.е. NPV различных проектов
можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех
остальных и позволяющее использовать его в качестве основного при анализе
оптимального инвестиционного портфеля.
Внутренняя норма доходности (IRR) является ставкой процентов, при которой чистая текущая
стоимость NPV равна 0.
Чем меньше ставка по кредитам или уровень дивидендов по сравнению с
нормой доходности, тем прибыльнее инвестиционный проект.
При сравнении инвестиционных проектов отбирается наилучший проект с
большей нормой доходности.
Индекс рентабельности (РI) рассчитывается по
формуле
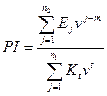 . (59)
. (59)
Если РI>1 , то
проект следует принять,
PI<1, то
проект следует отвергнуть;
PI=1 , то
проект ни прибыльный , ни убыточный.
В отличие от чистой текущей стоимости индекс рентабельности является относительным
показателем. Благодаря этому он очень
удобен при выборе одного проекта из ряда альтернативных, имеющих примерно
одинаковое значение NPV,
либо при комплектовании портфеля инвестиций с максимальным суммарным
значением NPV.
Пример 2. Показатели дисконтированных
сумм, денежных доходов и расходов по данным примера 1 имеют следующие значения. Вариант А – 377,1
и 214,9 тыс. руб. Вариант В – 386,2 и 223,1 тыс. руб. Подсчитаем РI .
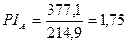
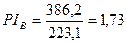 т.е. 75 и 73%
т.е. 75 и 73%
Индекс рентабельности инвестиций
характеризует некоторую дополнительную рентабельность, так как при ее расчете доходы и расходы уже
дисконтированы по ставке сравнения q. Если показатель РI равен единице, то это означает, что доходность
капиталовложений точно соответствует нормативу рентабельности q. При РI <1 инвестиции не рентабельны, так как не обеспечивают
этот норматив.
Рентабельность капитала (Рк) – соотношение чистой
прибыли (ЧП) ( за вычетом налогов) к собственному капиталу
(К). В условиях рынка рентабельность
капитала характеризует минимальную норму прибыльности капитальных вложений и
является более стабильным показателем, чем рентабельность продукции.
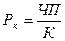 . (60)
. (60)
Срок окупаемости (Ток)
– это период времени, который необходим
для того, чтобы будущая прибыль (П)
предприятия достигла величины осуществленных
капитальных вложений (К).
Показатель срока окупаемости характеризует интенсивность возврата затраченных
средств на определенном интервале времени
после их вложения . Определяется без учета фактора времени по формуле
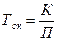 . (61)
. (61)
Абсолютная эффективность характеризует отношение эффекта (результата в
виде объема продукции или прибыли или
снижения затрат живого труда, себестоимости, материальных ресурсов, капитальных
вложений и оборотных средств, приводящего к росту продукции, прибыли) к
затратам на реализацию варианта,
отобранного по критериям. Расчет абсолютной эффективности завершает цикл выбора
наиболее эффективного варианта хозяйственного развития. Абсолютная
эффективность в отличие от сравнительной, всегда рассчитывается по фактическим
или ожидаемым показателям реализации варианта без приведения их в условный
сопоставимый вид.
В рыночной практике хозяйствования встречаются самые различные формы проявления
экономической эффективности. Технические и экономические аспекты эффективности
характеризуют развитие основных факторов производства и результативность их
использования. Социальная эффективность отражает решение конкретных социальных
задач (например, улучшение условий труда, охрану окружающей среды и т.д.).
Обычно социальные результаты точно связаны с экономическими .
В условиях рынка каждое предприятие, будучи экономически
самостоятельным товаропроизводителем, вправе использовать любые оценки
эффективности развития собственного производства в рамках установленных
государством налоговых отчислений и социальных ограничений. Особенности
функционирования рынка (субъективность интересов различных участников рыночного
процесса, неопределенность достижения конечных результатов, подвижность
параметров производства и сбыта продукции, множественность критериев оценки и
пр.) отторгают деление эффективности на общую и сравнительную, характерную для
отечественной теории и практики, поскольку возможности способа развития
производства и выбор наилучшего варианта зависят от рыночной конъюнктуры.
Рыночная же конъюнктура весьма сложна, и переход к рынку обуславливает важность
разработки единых подходов к измерению затрат и результатов для отбора и реализации
подлинно эффективных решений на всех уровнях управления производством, которые
превращают расчет экономической эффективности из формальной хозяйственной
процедуры в жизненную необходимость. [8, 553]
1.3.Применение индексного метода
Необходимость повышения эффективности производства как основного
фактора успешного функционирования
экономики предопределяется растущей конкуренцией со стороны
отечественных и зарубежных производителей, ограниченностью природных ресурсов и
приобретает особо важное значение в условиях рыночной экономики.
Характеризуется экономическая
эффективность общественного производства
соотношением результатов экономической деятельности с затратами факторов
производства, связанных с достижением этих результатов. Результатом производственной
деятельности на уровне отдельного предприятия служат валовой выпуск, валовая
добавленная стоимость.
Наиболее общим показателем повышения эффективности и интенсификации
общественного производства является рост производительности общественного труда,
увеличение доли прироста объема продукции, полученной за счет фактора, в общем
его приросте. Исходя из этого, особой
задачей статистики является определение влияния отдельных факторов на рост объема произведенной
продукции.
Использование индексного факторного анализа позволяет дать статистическую
оценку влияния различных факторов на динамику объема произведенной продукции.
Объем продукции является результативным показателем, зависящим от затрат
рабочего времени ( чел-часы, средняя списочная численность работников или
численность занятых в экономике) и общественной производительности труда:
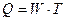 (62)
(62)
Т – затраты рабочего времени;
W – общественная производительность труда.
В этом соотношении (двухфакторной мультипликативной модели) затраты
рабочего времени являются экстенсивным фактором, а производительность труда –
интенсивным фактором.
Динамика объема продукции определяется изменением этих факторов. Влияние
всех прочих факторов (изменение фондоемкости продукции, улучшение организации
производства, сокращение потерь рабочего времени и т.п.) в конечном счете
отражается на изменении либо затрат труда, либо производительности труда.
Изменение объема продукции от изменения указанных факторов можно
исчислить так:
- в относительных величинах
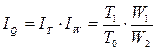 ; (63)
; (63)
в абсолютных величинах:
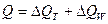 , (64)
, (64)
Рассчитывают абсолютные приросты объема продукции по следующим формулам:
1) за
счет изменения численности работников:
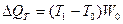 (65)
(65)
2) за
счет изменения производительности труда:
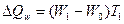 (66)
(66)
3) за
счет изменения двух факторов вместе: 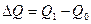 (67)
(67)
Для практических расчетов эти формулы преобразовывают, используя
относительные показатели роста объема продукции - 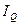 , затрат рабочего времени -
, затрат рабочего времени - 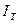 и
производительности труда -
и
производительности труда - 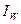 . Так как
. Так как 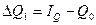 ,
, 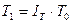 и
и 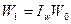 , после элементарных преобразований исходных формул
получим:
, после элементарных преобразований исходных формул
получим:
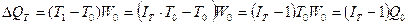 (68)
(68)
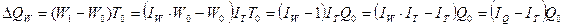 (69)
(69)
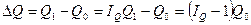 . (70)
. (70)
Доля каждого фактора в общем изменении объема продукции может быть
исчислена следующим образом
- доля прироста продукции за счет изменения затрат труда (dT)
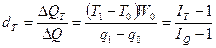 ; (71)
; (71)
доля прироста продукции за счет изменения производительности труда (dW)
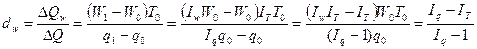 (72)
(72)
dT + dW = 1
Объем продукции может быть представлен также трехфакторной
мультипликативной моделью, так как
фондовооруженность (ФВ) и фондоотдача
(ФО) являются факторами роста
производительности труда 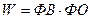 . (73)
. (73)
Эта трехфакторная мультипликативная модель имеет вид:
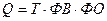 . (74)
. (74)
Количественную оценку изменения объема продукции под влиянием этих трех
факторов можно дать так:
- в относительных величинах
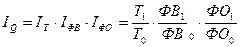 , (75)
, (75)
где 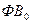 ,
, 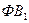 -
фондовооруженность в базисном и отчетном периодах соответственно;
-
фондовооруженность в базисном и отчетном периодах соответственно;
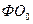 ,
, 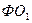 - фондоотдача в
базисном и отчетном периодах соответственно.
- фондоотдача в
базисном и отчетном периодах соответственно.
- в абсолютных величинах:

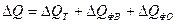 где (76)
где (76)
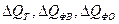 прирост объема
продукции за счет изменения численности работников, фондовооруженности и
фондоотдачи соответственно.
прирост объема
продукции за счет изменения численности работников, фондовооруженности и
фондоотдачи соответственно.
Прирост объема продукции за счет изменения численности работников равен:
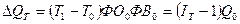 . (77)
. (77)
Прирост объема продукции за счет
изменения фондовооруженности равен:
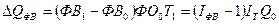 . (78)
. (78)
Прирост объема продукции за счет изменения фондоотдачи равен:
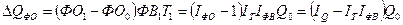 .
(79)
.
(79)
Анализ можно углубить. До сих пор анализ строился на характеристике
использования всех производственных основных фондов, но в процессе производства
продукции наибольшую роль играет активная их часть. Вычислив фондоотдачу,
исходя из активных фондов, получим четырехфакторную мультипликативную модель:
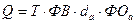 . (80)
. (80)
где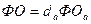 - фондоотдача;
- фондоотдача;
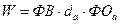 - производительность общественного труда;
- производительность общественного труда;
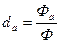 - доля активной части основных фондов в общей
стоимости основных фондов;
- доля активной части основных фондов в общей
стоимости основных фондов;
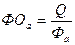 - фондоотдача
активной части основных фондов в общей стоимости основных фондов.
- фондоотдача
активной части основных фондов в общей стоимости основных фондов.
Количественную оценку изменения объема продукции под влиянием уже четырех
факторов можно будет дать следующим образом.
- в относительных величинах
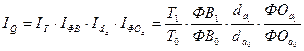 (81)
(81)
где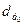
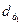 - доля активной
части основных фондов в базисном и отчетном периодах соответственно;
- доля активной
части основных фондов в базисном и отчетном периодах соответственно;
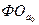 ,
, 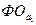 - фондоотдача в
базисном и отчетном периодах соответственно.
- фондоотдача в
базисном и отчетном периодах соответственно.
- в абсолютных величинах:

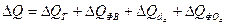 (82) где
(82) где
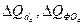 прирост объема
продукции за счет изменения доли активной части основных фондов и фондоотдачи
соответственно.
прирост объема
продукции за счет изменения доли активной части основных фондов и фондоотдачи
соответственно.
Прирост объема продукции за счет изменения численности работников равен:
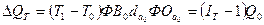 (83).
(83).
Прирост объема продукции за счет
изменения фондовооруженности равен:
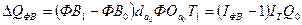 . (84)
. (84)
Прирост объема продукции за счет изменения доли активной части основных
фондов равен:
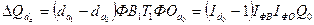 .
(85)
.
(85)
Прирост объема продукции за счет изменения фондоотдачи активной части
основных фондов равен:
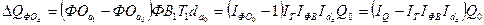 (86)
(86)
Более углубленный анализ может показать, например, что использование
активной части основных фондов не улучшилось, как это может быть видно из трехфакторной модели,
когда исходили из характеристики использования
производственных основных фондов, а ухудшилось, и, следовательно, нужно
предпринимать такие управленческие решения, которые выправили бы положение.
1.4.Применение
балансового метода
В статистике соотношение спроса и предложения (с некоторой степенью
точности) устанавливается с помощью
баланса спроса-предложения. Однако такой расчет можно осуществить только в
границах всего товарного рынка в целом.
Суть расчета в следующем: определяется объем товарного предложения (по
данным о поступлении или фактической продаже с необходимыми дорасчетами) и
покупательные фонды населения (доходы с корректировкой на прирост сбережений
минус обязательные платежи, представляющие совокупный спрос населения) (таблица
1):
Баланс
спроса и предложения.
|
Предложение
|
Спрос
|
|
1. объем
отечественного производства товаров потребительского назначения
2. объем
импорта
3. изменение
стоимости товарного поступления за счет роста цен
|
1. Денежные
доходы населения (за вычетом прироста сбережения, инвестиций в покупку ценных
бумаг и недвижимости, а также обязательных платежей)
2. Покупка
производственными предприятиями товаров для производственного потребления и
промышленной переработки
3. Покупка
товаров учреждениями и предприятиями
4. Изменение
стоимости купленных товаров за счет снижения цен
|
|
Итого
|
Итого
|
|
Сокращение
товарных запасов
|
Рост
товарных запасов
|
|
Баланс
|
Баланс
|
|
Дефицит
(П<С)
|
Дефицит
(П>С)
|
Итоговая строка отражает степень сбалансированности спроса и предложения.
Превышение предложения над спросом проявляется в росте товарных запасом, а
превышение спроса над предложением - в из сокращении. Этот факт используют для
косвенной оценки пропорциональности
рынка. Дело в том, что количественно оценить покупательский спрос на локальном
рынке какого-то товара практически не представляется возможным. Исключение
составляют биржевые рынки, где предложение и спрос регистрируются.
Сбалансированность спроса и предложения обусловливает стабильность
товарных запасов. Товарные запасы могут выполнять функцию индикатора
конъюнктуры рынка. В этом случае можно использовать абсолютный показатель объема
товарных запасов, но более точным будет
относительный показатель запасов товарооборота (в днях):
Is = 1
> П = С (рынок - сбалансирован)
Is
> 1 > П > С (диспропорция: предложение превышает спрос);
Is
< 1 > П < С (диспропорция: спрос
превышает предложение),
Где Is - индекс
товарных запасов, П - предложение, С - спрос.
Существует ряд других приемов исследования конъюнктуры рынка, но их суть
неизменна - сопоставление между собой индикаторов рынка и индексов деловой
активности, оценка спроса и предложения.
Заключение
Рыночная статистика удовлетворяет
информационно-аналитические потребности государственных структур, которые
ставят перед собой цели прямого или косвенного регулирования рынка, контроль за
параметрами его развития, а также разработку и проведение в жизнь
социально-экономической политики. Она также обеспечивает методологические и
аналитические потребности служб маркетинга и маркетингового исследования,
которые, в свою очередь, дают рекомендации менеджменту для принятия оптимальных
управленческих решений. Кроме того, статистика рынка способствует дальнейшему
развитию и совершенствованию экономической теории, поскольку она не только
информационно иллюстрирует ее дефиниции, но и выявляет новые закономерности и
тенденции, подтверждая или отрицая выдвинутые гипотезы и положения. Наконец,
статистика рынка играет роль информатора общественности о характере развития
рынка, о тех или иных рыночных процессах, в которых сильно заинтересовано общество в целом или отдельные его слои.
Статистика изучает рынок, процесс движения товаров в экономическом и
географическом пространстве, их обмен на деньги по ценам, складывающимся в
соответствии с действием рыночного механизма, материально-техническое и
ресурсное обеспечение этого процесса, социально-экономические результаты его
функционирования.
Однако известной особенностью статистики является то, что она изучает
массовые явления и процессы, которые могут быть выражены количественно.
Действие рыночного механизма проявляется в вероятностных, стохастических
процессах, что обеспечивает возможность использования ряда
математико-статистических методов в целях изучения рынка.
Предмет статистики рынка - это массовые рыночные явления и процессы,
поддающиеся количественной оценке.
Таким образом, в данной курсовой рассмотрены такие понятия как: Спрос,
предложение, конкуренция, рыночная конъюнктура, система показателей, а также
маркетинг и маркетинговые исследования.
Я считаю, что рынок - это стихийное явление, которое нуждается в
умеренном регулировании, вмешательстве со стороны государства. И для того,
чтобы это вмешательство было безболезненным и верным, необходимо изучать и
знать основные процессы и ситуации, в которых происходит взаимодействие
участников рынка.
|
|
|
|
|
Таблица 1.
|
|
Исходные
данные
|
|
|
|
|
|
|
|
№ п/п
|
Рейтинг района города по удаленности
от центра
|
Цена 1кв.м общей площади квартиры,
у.е.
|
|
|
|
|
|
|
17
|
6
|
117,0
|
min
|
|
|
|
|
|
13
|
3
|
138,9
|
|
|
|
|
|
|
29
|
3
|
157,9
|
|
|
|
|
|
|
3
|
2
|
177,6
|
|
|
|
|
|
|
2
|
5
|
186,7
|
|
|
|
|
|
|
8
|
3
|
187,3
|
|
|
|
|
|
|
11
|
6
|
187,3
|
|
|
|
|
|
|
23
|
5
|
193,3
|
|
|
|
|
|
|
22
|
5
|
210,5
|
|
|
|
|
|
|
15
|
4
|
256,2
|
|
|
|
|
|
|
28
|
5
|
266,7
|
|
|
|
|
|
|
16
|
4
|
266,9
|
|
|
|
|
|
|
25
|
4
|
267,8
|
|
|
|
|
|
|
33
|
4
|
284,2
|
|
|
|
|
|
|
31
|
4
|
286,1
|
|
|
|
|
|
|
18
|
6
|
293,9
|
|
|
|
|
|
|
5
|
5
|
310,2
|
|
|
|
|
|
|
6
|
6
|
321,0
|
|
|
|
|
|
|
26
|
2
|
340,9
|
|
|
|
|
|
|
20
|
2
|
350,0
|
|
|
|
|
|
|
34
|
3
|
350,0
|
|
|
|
|
|
|
39
|
4
|
350,1
|
|
|
|
|
|
|
30
|
2
|
359,2
|
|
|
|
|
|
|
1
|
2
|
361,1
|
|
|
|
|
|
|
40
|
2
|
363,0
|
|
|
|
|
|
|
32
|
1
|
380,8
|
|
|
|
|
|
|
12
|
1
|
386,1
|
|
|
|
|
|
|
7
|
3
|
390,4
|
|
|
|
|
|
|
35
|
3
|
392,5
|
|
|
|
|
|
|
38
|
1
|
394,1
|
|
|
|
|
|
|
27
|
2
|
394,9
|
|
|
|
|
|
|
37
|
3
|
402,8
|
|
|
|
|
|
|
9
|
2
|
403,1
|
|
|
|
|
|
|
21
|
2
|
405,2
|
|
|
|
|
|
|
4
|
1
|
406,4
|
|
|
|
|
|
|
10
|
1
|
433,3
|
|
|
|
|
|
|
24
|
1
|
437,5
|
|
|
|
|
|
|
36
|
2
|
480,5
|
|
|
|
|
|
|
14
|
1
|
481,4
|
|
|
|
|
|
|
19
|
1
|
500,0
|
max
|
|
|
|
|
Задание 1
|
|
|
|
|
|
|
По
исходным данным (табл.1) необходимо выполнить следующее:
|
|
|
1.
Построить статистический ряд распределения банков по цене 1 кв.м общей
площади квартиры, образовав шесть групп с равными
интервалами.
|
|
2.
Графическим методом и путем расчётов определить значения моды и медианы
полученного ряда распределения.
|
|
3.
Рассчитать характеристики ряда распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации.
|
|
4.
Вычислить среднюю арифметическую по исходным данным (табл. 1.1),
сравнить её с аналогичным показателем, рассчитанным в п. 3 для интервального
ряда распределения. Объяснить причину их расхождения.
|
|
Сделать
выводы по результатам выполнения Задания
1.
|
Выполнение
Задания 1
Целью
выполнения данного Задания является изучение состава и структуры выборочной
совокупности банков путем построения и анализа статистического ряда
распределения банков по признаку цена 1 кв.м
общей площади квартиры.
1.Построение интервального ряда
распределения квартир по цене 1кв.м общей стоимости квартиры.
Для построения
интервального вариационного ряда, характеризующего распределение банков по
объему кредитных вложений, необходимо вычислить величину и границы
интервалов ряда.
При построении
ряда с равными интервалами величина интервала h определяется по формуле
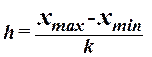 ,
(1)
,
(1)
где 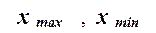 – наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
– наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
Число групп k задается в условии задания ( k=6) или рассчитывается по
формуле Г.Стерджесса
k=1+3,322 lg n,
(2)
где n - число единиц совокупности.
Определение величины интервала по
формуле (1) при заданных k = 6,
xmax = 500,0
у.е. за 1 кв.м., xmin = 117,0 у.е. за 1 кв.м.:
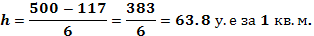
При h = 63,8 у.е. за 1 кв. м общей площади
квартиры границы интервалов ряда распределения имеют следующий вид (табл. 2):
|
|
|
|
|
|
Таблица 2
|
|
Номер группы
|
Нижняя граница, у.е. за 1 кв. м.
|
Верхняя граница, у.е. за 1 кв. м.
|
|
|
|
|
|
1
|
117,0
|
180,8
|
|
|
|
|
|
2
|
180,8
|
244,7
|
|
|
|
|
|
3
|
244,7
|
308,5
|
|
|
|
|
|
4
|
308,5
|
372,3
|
|
|
|
|
|
5
|
372,3
|
436,2
|
|
|
|
|
|
6
|
436,2
|
500,0
|
|
|
|
|
Для
построения интервального ряда необходимо подсчитать число банков, входящих в
каждую группу (частоты групп). При этом возникает вопрос, в какую группу
включать единицы совокупности, у которых значения признака выступают
одновременно и верхней, и нижней границами смежных интервалов (для демонстрационного
примера – это 180,8, 244,7, 308,5, 372,3, 436,2 у.е. за 1 кв.м.). Отнесение
таких единиц к одной из двух смежных групп рекомендуется осуществлять по
принципу полуоткрытого интервала [
). Т.к. при этом верхние границы интервалов не принадлежат данным
интервалам, то соответствующие им единицы совокупности включаются не в данную
группу, а в следующую. В последний интервал включаются и нижняя,
и верхняя границы.
Процесс
группировки единиц совокупности по признаку Цена за 1 кв.м общей площади
квартиры представлен во вспомогательной (разработочной) таблице 3 (графа 4
этой таблицы необходима для построения аналитической группировки в Задании 2).
Таблица 3
Разработочная таблица для построения
интервального ряда распределения и аналитической группировки
|
Группы районов по цене за 1 кв.м общей
площади квартиры
|
Номер района
|
Цена 1 кв.м общей площади квартиры
|
Рейтинг района города по удаленности от
центра
|
|
1
|
2
|
3
|
4
|
|
177,0-180,8
|
17
|
117,0
|
6
|
|
13
|
138,9
|
3
|
|
29
|
157,9
|
3
|
|
3
|
177,6
|
2
|
|
Всего
|
4
|
591,4
|
14
|
|
180,8-244,7
|
2
|
186,7
|
5
|
|
8
|
187,3
|
3
|
|
11
|
187,3
|
6
|
|
23
|
193,3
|
5
|
|
22
|
210,5
|
5
|
|
Всего
|
5
|
965,1
|
24
|
|
15
|
256,2
|
4
|
|
244,7-308,5
|
28
|
266,7
|
5
|
|
16
|
266,9
|
4
|
|
25
|
267,8
|
4
|
|
33
|
284,2
|
4
|
|
31
|
286,1
|
4
|
|
18
|
293,9
|
6
|
|
Всего
|
7
|
1921,8
|
31
|
|
5
|
310,2
|
5
|
|
308,5-372,3
|
6
|
321,0
|
6
|
|
26
|
340,9
|
2
|
|
20
|
350,0
|
2
|
|
34
|
350,0
|
3
|
|
39
|
350,1
|
4
|
|
30
|
359,2
|
2
|
|
1
|
361,1
|
2
|
|
40
|
363,0
|
2
|
|
Всего
|
9
|
3105,5
|
28
|
|
32
|
380,8
|
1
|
|
12
|
386,1
|
1
|
|
372,3-436,2
|
7
|
390,4
|
3
|
|
35
|
392,5
|
3
|
|
38
|
394,1
|
1
|
|
27
|
394,9
|
2
|
|
37
|
402,8
|
3
|
|
9
|
403,1
|
2
|
|
21
|
405,2
|
2
|
|
4
|
406,4
|
1
|
|
10
|
433,3
|
1
|
|
Всего
|
11
|
4389,6
|
20
|
|
24
|
437,5
|
1
|
|
436,2-500,0
|
36
|
480,5
|
2
|
|
14
|
481,4
|
1
|
|
19
|
500,0
|
1
|
|
Всего
|
4
|
1899,4
|
5
|
|
ИТОГО
|
40
|
12872,8
|
122
|
На основе
групповых итоговых строк «Всего» табл. 3 формируется итоговая таблица 4,
представляющая интервальный ряд распределения районов по цене квартир за 1кв.м от
общей площади квартиры .
Таблица 4
Распределение
районов по цене квартир за 1кв.м от общей площади квартиры
|
Номер группы
|
Группы районов по цене за 1 кв.м общей
площади квартиры
|
Число районов,
f
|
|
1
|
177,0-180,8
|
4
|
|
2
|
180,8-244,7
|
5
|
|
3
|
244,7-308,5
|
7
|
|
4
|
308,5-372,3
|
9
|
|
5
|
372,3-436,2
|
11
|
|
6
|
436,2-500,0
|
4
|
|
|
Всего
|
40
|
Помимо
частот групп в абсолютном выражении в анализе интервальных рядов используются
ещё три характеристики ряда, приведенные в графах 4 - 6 табл. 1.4. Это частоты групп в относительном выражении,
накопленные (кумулятивные) частоты Sj, получаемые путем последовательного
суммирования частот всех предшествующих (j-1) интервалов, и накопленные частости, рассчитываемые
по формуле 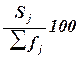 .
.
Таблица 5
Структура районов по цене квартир за 1 кв.м общей площади квартир
|
№ группы
|
Группы районов по цене за 1 кв.м общей
площади квартиры, у.е
|
Число банков, fi
|
Накопленная частота, Si
|
Накопленная частость,%
|
|
в абсолютном
выражении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
177,0-180,8
|
4
|
10,0
|
4
|
10,0
|
|
2
|
180,8-244,7
|
5
|
12,5
|
9
|
22,5
|
|
3
|
244,7-308,5
|
7
|
17,5
|
16
|
40,0
|
|
4
|
308,5-372,3
|
9
|
22,5
|
25
|
62,5
|
|
5
|
372,3-436,2
|
11
|
27,5
|
36
|
90,0
|
|
6
|
436,2-500,0
|
4
|
10,0
|
40
|
100,0
|
|
|
Итого
|
40
|
100,0
|
|
|
Вывод. Анализ
интервального ряда распределения изучаемой совокупности районов показывает, что
распределение районов по цене квартир за 1кв.м не является равномерным:
преобладают районы с с ценами квартир за 1 кв.м от 372,3 у.е. за 1кв.м. до 436,2
у.е. за 1 кв.м. (это 11 районов, доля которых составляет 27,5%); 62,5% банков
имеют кредитные вложения менее 372,3
у.е. за 1кв.м., а 90,0% – менее 436,2 у.е. за 1 кв.м.
1.2. Нахождение моды и медианы полученного интервального ряда
распределения графическим методом и
путем расчетов
Мода и
медиана являются структурными средними величинами, характеризующими
(наряду со средней арифметической) центр распределения единиц совокупности по
изучаемому признаку.
Мода Мо
для дискретного ряда – это значение признака, наиболее часто встречающееся
у единиц исследуемой совокупности[1].
В интервальном вариационном ряду модой приближенно считается центральное
значение модального интервала (имеющего наибольшую частоту). Более
точно моду можно определить графическим методом по гистограмме ряда (рис.1).


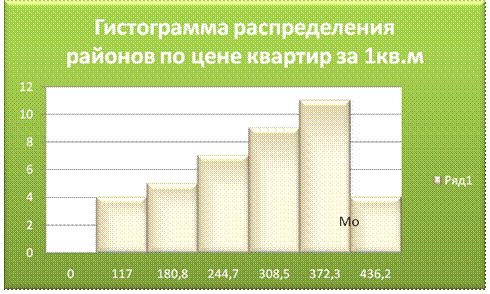
Рис. 1
Определение моды графическим методом
Конкретное
значение моды для интервального ряда рассчитывается по формуле:
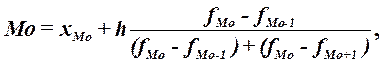 (3)
(3)
где хМo – нижняя
граница модального интервала,
h
–величина модального интервала,
fMo
– частота модального интервала,
fMo-1
– частота интервала, предшествующего модальному,
fMo+1
– частота интервала, следующего за модальным.
Согласно
табл.1.3 модальным интервалом построенного ряда является интервал 140 – 190
млн. руб., так как его частота максимальна (f3 = 12).
Расчет моды
по формуле (3):
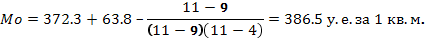
Вывод. Для рассматриваемой совокупности
районов наиболее распространенная цена кварир за 1 кв.м характеризуется средней
величиной 386,5 у.е. за 1 кв.м.
Медиана
Ме – это значение признака, приходящееся на середину ранжированного
ряда. По обе стороны от медианы находится одинаковое количество единиц
совокупности.
Медиану можно
определить графическим методом по кумулятивной кривой (рис. 2). Кумулята
строится по накопленным частотам (табл. 5, графа 5).



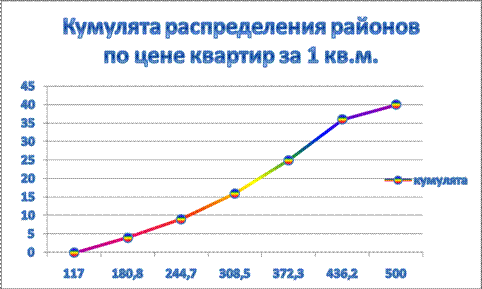
Рис. 2.
Определение медианы графическим методом
Конкретное значение медианы для интервального ряда рассчитывается по
формуле:
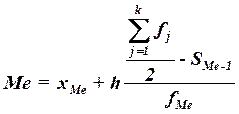 , (4)
, (4)
где хМе– нижняя граница
медианного интервала,
h – величина медианного
интервала,
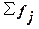 – сумма всех частот,
– сумма всех частот,
fМе – частота
медианного интервала,
SMе-1 –
кумулятивная (накопленная) частота интервала, предшествующего медианному.
Для расчета
медианы необходимо, прежде всего, определить медианный интервал, для чего
используются накопленные частоты (или частости) из табл. 5 (графа 5). Так как
медиана делит численность ряда пополам, она будет располагаться в том
интервале, где накопленная частота впервые равна полусумме всех частот 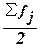 или превышает
ее (т.е. все предшествующие накопленные
частоты меньше этой величины).
или превышает
ее (т.е. все предшествующие накопленные
частоты меньше этой величины).
В данной
задаче медианным интервалом является интервал
308,5-372,3 у.е., так как именно в этом
интервале накопленная частота Sj = 25 впервые превышает величину, равную половине
численности единиц совокупности (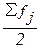 =
= 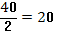 ).
).
Расчет
значения медианы по формуле (4):
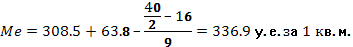
Вывод. В рассматриваемой совокупности
районов половина районов имеют в среднем цены за 1 кв. м от общей площади
квартир не более 336,9 у.е. а другая половина – не менее 336,9 у.е.
3. Расчет характеристик ряда распределения
Для расчета
характеристик ряда распределения 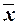 , σ, σ2, Vσ на основе
табл. 5 строится вспомогательная таблица 6 (
, σ, σ2, Vσ на основе
табл. 5 строится вспомогательная таблица 6 (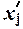 – середина j-го интервала).
– середина j-го интервала).
Таблица
6
Расчетная таблица для нахождения
характеристик ряда распределения
|
Группы районов по цене за 1 кв.м общей
площади квартиры, у.е
|
Середина интервала, x'j
|
Число районов, fj
|
x'jfj
|
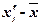
|
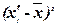
|
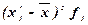
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
177,0-180,8
|
178,9
|
4
|
715,6
|
-125,8
|
15825,64
|
63302,56
|
|
|
180,8-244,7
|
212,75
|
5
|
1063,75
|
-91,95
|
8454,8025
|
42274,0125
|
|
|
244,7-308,5
|
276,6
|
7
|
1936,2
|
-28,1
|
789,61
|
5527,27
|
|
|
308,5-372,3
|
340,4
|
9
|
3063,6
|
35,7
|
1274,49
|
11470,41
|
|
|
372,3-436,2
|
404,25
|
11
|
4446,75
|
99,55
|
9910,2025
|
109012,2275
|
|
|
436,2-500,0
|
468,1
|
4
|
1872,4
|
163,4
|
26699,56
|
106798,24
|
|
|
Сумма
|
|
43
|
13102,3
|
|
|
338391,72
|
|
Расчет
средней арифметической взвешенной:
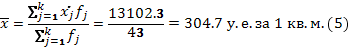
Расчет средней арифметической взвешенной:
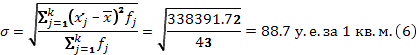
Расчет
дисперсии: 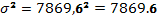
Расчет
коэффициента вариации: 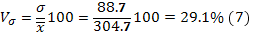
Вывод. Анализ полученных значений
показателей 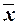 и σ
говорит о том, что цена 1 кв.м. общей площади квартир составляет304,7 у.е.,
отклонение от средней цены в ту или иную сторону составляет в среднем 88,7 у.е.
(или 29,1%), наиболее характерные значения цены 1 кв. м. общей площади
квартир находятся в пределах от 215,9 у.е. до 393,4 у.е. (диапазон
и σ
говорит о том, что цена 1 кв.м. общей площади квартир составляет304,7 у.е.,
отклонение от средней цены в ту или иную сторону составляет в среднем 88,7 у.е.
(или 29,1%), наиболее характерные значения цены 1 кв. м. общей площади
квартир находятся в пределах от 215,9 у.е. до 393,4 у.е. (диапазон 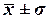 ).
).
Значение Vσ = 29,1% не превышает 33%, следовательно,
вариация цен квартир в исследуемой совокупности районов незначительна и
совокупность по данному признаку качественно однородна. Расхождение между
значениями 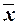 , Мо и Ме незначительно (
, Мо и Ме незначительно (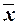 =304,7 у.е., Мо=386,5
у.е., Ме=336,6 у.е.), что
подтверждает вывод об однородности совокупности банков. Таким образом,
найденное среднее значение цен 1
кв. м. общей
площади квартир (304,7 у.е.) является типичной, надежной характеристикой
исследуемой совокупности районов.
=304,7 у.е., Мо=386,5
у.е., Ме=336,6 у.е.), что
подтверждает вывод об однородности совокупности банков. Таким образом,
найденное среднее значение цен 1
кв. м. общей
площади квартир (304,7 у.е.) является типичной, надежной характеристикой
исследуемой совокупности районов.
4.Вычисление
средней арифметической по исходным данным
Для расчета
применяется формула средней арифметической простой:
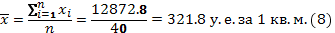
Причина
расхождения средних величин, рассчитанных по формулам (8) и (5), заключается в
том, что по формуле (8) средняя определяется по фактическим значениям
исследуемого признака для
всех 40-ка районов, а по формуле
(5) средняя вычисляется для интервального ряда, когда в качестве значений
признака берутся середины интервалов 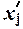 и,
следовательно, значение средней будет менее точным (за исключением случая
равномерного распределения значений признака внутри каждой группы).
и,
следовательно, значение средней будет менее точным (за исключением случая
равномерного распределения значений признака внутри каждой группы).
Задание 2
По исходным данным табл.
1 с использованием результатов выполнения Задания 1 необходимо выполнить
следующее:
1.
Установить
наличие и характер корреляционной связи между признаками Рейтинг районов города по удаленности от центра и Цена 1 кв. м. общей площади квартир, образовав
по каждому признаку четыре группы с равными интервалами, используя методы:
а) аналитической группировки;
б) корреляционной
таблицы.
2.
Оценить
тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое
корреляционное отношение.
Сделать выводы по результатам выполнения Задания 2.
Выполнение Задания
2
Целью
выполнения данного Задания является выявление наличия корреляционной связи
между факторным и результативным признаками, установление направления связи и
оценка ее тесноты.
Факторный и результативный признаки либо задаются в условии
задания, либо определяются путем проведения предварительного теоретического
анализа. Лишь после того, как выяснена экономическая сущность явления и
определены факторный и результативный признаки, приступают к проведению
корреляционного анализа данных.
По условию Задания 2 факторным является признак Рейтинг раойнов города по удаленности от
центра (X), результативным – признак Цена 1 кв. м. общей площади
квартир (Y).
1. Установление наличия и характера связи между признаками Рейтинг районов города по удаленности от
центра и Цена 1 кв. м. общей площади
квартир методами аналитической группировки и корреляционной таблицы
1а. Применение метода аналитической группировки
При использовании метода аналитической группировки строится
интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой j-ой группы ряда определяется
среднегрупповое значение 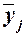 результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения 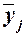 систематически
возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую
группировку, характеризующую зависимость между факторным признаком Х – Рейтинг
районов горда по удаленности от центра и
результативным признаком Y – Цена
1 кв. м.
общей площади квартир. Макет аналитической таблицы имеет следующий вид
(табл. 7):
Таблица 7
Зависимость суммы прибыли банков от объема кредитных
вложений
|
Номер группы
|
Рейтинг районов по удаленности от центра
|
Число районов
|
Цена 1 кв. м., у.е.
|
|
Всего
|
в среднем на 1 кв. м., 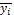
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
6
|
|
|
|
|
|
Итого:
|
|
|
|
|
Групповые средние значения 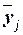 получаем из таблицы 7.1 (графа 3). Построенную
аналитическую группировку представляет табл. 8.
получаем из таблицы 7.1 (графа 3). Построенную
аналитическую группировку представляет табл. 8.
Таблица 7.1.
|
Рейтинг района города по удаленности от
центра
|
Цена 1кв.м общей площади квартиры, у.е.
|
Средняя по
группе, у.е.
|
|
1
|
380,8
|
|
|
1
|
386,1
|
|
|
1
|
394,1
|
|
|
1
|
406,4
|
|
|
1
|
433,3
|
|
|
1
|
437,5
|
|
|
1
|
481,4
|
|
|
1
|
500,0
|
max
|
|
8
|
3419,6
|
427,5
|
|
2
|
177,6
|
|
|
2
|
340,9
|
|
|
2
|
350,0
|
|
|
2
|
359,2
|
|
|
2
|
361,1
|
|
|
2
|
363,0
|
|
|
2
|
394,9
|
|
|
2
|
403,1
|
|
|
2
|
405,2
|
|
|
2
|
480,5
|
|
|
10
|
3635,5
|
363,6
|
|
3
|
138,9
|
|
|
3
|
157,9
|
|
|
3
|
187,3
|
|
|
3
|
350,0
|
|
|
3
|
390,4
|
|
|
3
|
392,5
|
|
|
3
|
402,8
|
|
|
7
|
2019,8
|
288,5
|
|
4
|
256,2
|
|
|
4
|
266,9
|
|
|
4
|
267,8
|
|
|
4
|
284,2
|
|
|
4
|
286,1
|
|
|
4
|
350,1
|
|
|
6
|
1711,3
|
285,2
|
|
5
|
186,7
|
|
|
5
|
193,3
|
|
|
5
|
210,5
|
|
|
5
|
266,7
|
|
|
5
|
310,2
|
|
|
5
|
1167,4
|
233,5
|
|
6
|
117,0
|
min
|
|
6
|
187,3
|
|
|
6
|
293,9
|
|
|
6
|
321,0
|
|
|
4
|
919,2
|
229,8
|
Таблица 8
Зависимость суммы Цены 1 кв. м. общей площади
квартир от рейтинга района города по удаленности от центра
|
Номер группы
|
Рейтинг районов по удаленности от ентра
|
Число районов
|
Цена 1 кв. м., у.е.
|
|
Всего
|
в среднем на 1 кв. м.¯(y_i )
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
1
|
8
|
3419,6
|
427,5
|
|
2
|
2
|
10
|
3635,5
|
363,6
|
|
3
|
3
|
7
|
2019,8
|
288,5
|
|
4
|
4
|
6
|
1711,3
|
285,2
|
|
5
|
5
|
5
|
1167,4
|
233,5
|
|
6
|
6
|
4
|
919,2
|
229,8
|
|
Итого:
|
|
40
|
12872,8
|
1828,0
|
Вывод. Анализ данных табл. 8 показывает, что с увеличением рейтинга
районов от группы к группе систематически уменьшается цена 1 кв. м., что
свидетельствует о наличии обратной корреляционной связи между исследуемыми
признаками.
1б.
Применение метода корреляционной таблицы.
Корреляционная
таблица представляет собой комбинацию двух рядов распределения. Строки таблицы
соответствуют группировке единиц совокупности по факторному признаку Х, а графы – группировке единиц по
результативному признаку Y. На пересечении j-ой строки и k-ой графы
указывается число единиц совокупности, входящих в j-ый интервал по факторному
признаку и в k-ый
интервал по результативному признаку. Концентрация частот около диагонали
построенной таблицы свидетельствует о наличии корреляционной связи между
признаками. Связь прямая, если частоты располагаются по диагонали, идущей от
левого верхнего угла к правому нижнему. Расположение частот по диагонали от
правого верхнего угла к левому нижнему говорит об обратной связи.
Для
построения корреляционной таблицы необходимо знать величины и границы
интервалов по двум признакам X и Y. Величина интервала и границы
интервалов для факторного
признака Х – Рейтинг районов по
удаленности от центра известны из табл. 8. Для результативного признака Y – Цена
1 кв. м.
общей площади квартир величина интервала h=63.8
Границы интервалов ряда распределения
результативного признака Y имеют следующий вид (табл. 9):
Таблица
9
|
Номер группы
|
Нижняя граница,
у.е. за 1 кв. м.
|
Верхняя граница,
у.е. за 1 кв. м.
|
|
1
|
117,0
|
180,8
|
|
2
|
180,8
|
244,7
|
|
3
|
244,7
|
308,5
|
|
4
|
308,5
|
372,3
|
|
5
|
372,3
|
436,2
|
|
6
|
436,2
|
500,0
|
Подсчитывая
с использованием принципа полуоткрытого интервала [ ) число банков, входящих в каждую
группу (частоты групп), получаем интервальный ряд распределения
результативного признака (табл. 10).
Таблица 10
Распределение районов по цене 1 кв.м. общей
площади квартир
|
Группы цен за 1 кв. м, у.е. x
|
Число районов,
f
|
|
117,0-180,8
|
4
|
|
180,8-244,7
|
5
|
|
244,7-308,5
|
7
|
|
308,5-372,3
|
9
|
|
372,3-436,2
|
11
|
|
436,2-500,0
|
4
|
|
Всего
|
40
|
Используя
группировки по факторному и результативному признакам, строим корреляционную
таблицу (табл. 11).
Таблица
11
Корреляционная таблица зависимости цены 1 кв. м. общей площади
квартир в зависимости от рейтинга района
|
Группы районов по цене за 1 кв.м общей
площади квартиры, у.е
|
Рейтинг районов по удаленности от центра
|
|
1
|
2
|
3
|
4
|
5
|
6
|
Итого
|
|
177,0-180,8
|
|
1
|
2
|
|
|
1
|
4
|
|
180,8-244,7
|
|
|
1
|
|
3
|
1
|
5
|
|
244,7-308,5
|
|
|
|
5
|
1
|
1
|
7
|
|
308,5-372,3
|
|
5
|
1
|
1
|
1
|
1
|
9
|
|
372,3-436,2
|
5
|
3
|
3
|
|
|
|
11
|
|
436,2-500,0
|
3
|
1
|
|
|
|
|
4
|
|
Итого
|
8
|
10
|
7
|
6
|
5
|
4
|
40
|
Вывод. Анализ данных табл. 11
показывает, что распределение частот групп произошло вдоль диагонали, идущей из
правого верхнего угла в левый нижний угол таблицы. Это свидетельствует о
наличии обратной корреляционной связи между рейтингом района и ценой за 1 кв. м. общей площади
квартир.
2. Измерение тесноты корреляционной
связи с использованием коэффициента детерминации и эмпирического корреляционного
отношения
Для измерения
тесноты связи между факторным и результативным признаками рассчитывают
специальные показатели – эмпирический коэффициент детерминации 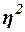 и эмпирическое
корреляционное отношение
и эмпирическое
корреляционное отношение 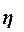 .
.
Эмпирический
коэффициент детерминации 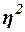 оценивает,
насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель
оценивает,
насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель 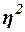 рассчитывается
как доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается
как доля межгрупповой дисперсии в общей дисперсии по формуле
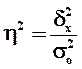 ,
(9)
,
(9)
где 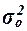 – общая
дисперсия признака Y,
– общая
дисперсия признака Y,
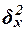 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Значения
показателя 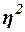 изменяются в
пределах
изменяются в
пределах 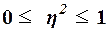 . При отсутствии корреляционной связи между признаками
Х и Y имеет место равенство
. При отсутствии корреляционной связи между признаками
Х и Y имеет место равенство 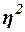 =0, а
при наличии функциональной связи между ними - равенство
=0, а
при наличии функциональной связи между ними - равенство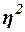 =1.
=1.
Общая
дисперсия 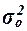 характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y
факторов (систематических и случайных). Этот показатель вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y
факторов (систематических и случайных). Этот показатель вычисляется по формуле
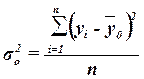 ,
(10)
,
(10)
где yi – индивидуальные значения результативного
признака;
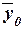 – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Общая средняя
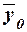 вычисляется как
средняя арифметическая простая по всем единицам совокупности:
вычисляется как
средняя арифметическая простая по всем единицам совокупности:
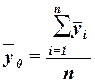 (11)
(11)
или как средняя взвешенная по частоте групп интервального
ряда:
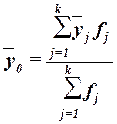 (12)
(12)
Для вычисления 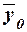 удобно
использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются
значения числителя и знаменателя формулы.
удобно
использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются
значения числителя и знаменателя формулы.
Расчет 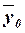 по формуле
(11):
по формуле
(11): 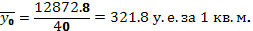
Для расчета
общей дисперсии 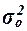 применяется
вспомогательная таблица 12.
применяется
вспомогательная таблица 12.
Таблица 12
Вспомогательная таблица для расчета общей
дисперсии
|
1
|
2
|
3
|
4
|
5
|
|
1
|
361,1
|
39,3
|
1544,49
|
130393,2
|
|
2
|
186,7
|
-135,1
|
18252,01
|
34856,89
|
|
3
|
177,6
|
-144,2
|
20793,64
|
31541,76
|
|
4
|
406,4
|
84,6
|
7157,16
|
165161
|
|
5
|
310,2
|
-11,6
|
134,56
|
96224,04
|
|
6
|
321
|
-0,8
|
0,64
|
103041
|
|
7
|
390,4
|
68,6
|
4705,96
|
152412,2
|
|
8
|
187,3
|
-134,5
|
18090,25
|
35081,29
|
|
9
|
403,1
|
81,3
|
6609,69
|
162489,6
|
|
10
|
433,3
|
111,5
|
12432,25
|
187748,9
|
|
11
|
187,3
|
-134,5
|
18090,25
|
35081,29
|
|
12
|
386,1
|
64,3
|
4134,49
|
149073,2
|
|
13
|
138,9
|
-182,9
|
33452,41
|
19293,21
|
|
14
|
481,4
|
159,6
|
25472,16
|
231746
|
|
15
|
256,2
|
-65,6
|
4303,36
|
65638,44
|
|
16
|
266,9
|
-54,9
|
3014,01
|
71235,61
|
|
17
|
117
|
-204,8
|
41943,04
|
13689
|
|
18
|
293,9
|
-27,9
|
778,41
|
86377,21
|
|
19
|
500
|
178,2
|
31755,24
|
250000
|
|
20
|
350
|
28,2
|
795,24
|
122500
|
|
21
|
405,2
|
83,4
|
6955,56
|
164187
|
|
22
|
210,5
|
-111,3
|
12387,69
|
44310,25
|
|
23
|
193,3
|
-128,5
|
16512,25
|
37364,89
|
|
24
|
437,5
|
115,7
|
13386,49
|
191406,3
|
|
25
|
267,8
|
-54
|
2916
|
71716,84
|
|
26
|
340,9
|
19,1
|
364,81
|
116212,8
|
|
27
|
394,9
|
73,1
|
5343,61
|
155946
|
|
28
|
266,7
|
-55,1
|
3036,01
|
71128,89
|
|
29
|
157,9
|
-163,9
|
26863,21
|
24932,41
|
|
30
|
359,2
|
37,4
|
1398,76
|
129024,6
|
|
31
|
286,1
|
-35,7
|
1274,49
|
81853,21
|
|
32
|
380,8
|
59
|
3481
|
145008,6
|
|
33
|
284,2
|
-37,6
|
1413,76
|
80769,64
|
|
34
|
350
|
28,2
|
795,24
|
122500
|
|
35
|
392,5
|
70,7
|
4998,49
|
154056,3
|
|
36
|
480,5
|
158,7
|
25185,69
|
230880,3
|
|
37
|
402,8
|
81
|
6561
|
162247,8
|
|
38
|
394,1
|
72,3
|
5227,29
|
155314,8
|
|
39
|
350,1
|
28,3
|
800,89
|
122570
|
|
40
|
363
|
41,2
|
1697,44
|
131769
|
|
Итого
|
12872,8
|
0,8
|
394058,9
|
4536783
|
Расчет
общей дисперсии по формуле (10):
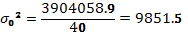
Общая дисперсия может быть также рассчитана
по формуле
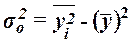 ,
,
где 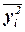 – средняя из
квадратов значений результативного признака,
– средняя из
квадратов значений результативного признака,
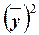 – квадрат
средней величины значений результативного признака.
– квадрат
средней величины значений результативного признака.
Для
демонстрационного примера 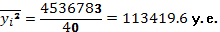
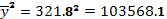
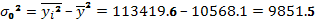
Межгрупповая дисперсия 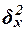 измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х
(по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в
отклонении групповых средних
измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х
(по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в
отклонении групповых средних 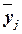 от общей
средней
от общей
средней 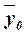 . Показатель
. Показатель 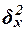 вычисляется по
формуле
вычисляется по
формуле
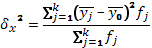
где 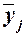 –групповые
средние,
–групповые
средние,
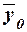 – общая
средняя,
– общая
средняя,
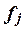 –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета
межгрупповой дисперсии 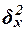 строится вспомогательная таблица 13 При этом
используются групповые средние значения
строится вспомогательная таблица 13 При этом
используются групповые средние значения 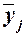 из табл. 8
(графа 5).
из табл. 8
(графа 5).
|
Группы цен за 1 кв. м, у.е.
|
Число районов,
f
|
среднее значение
в группе
|
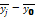
|
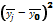
|
|
117,0-180,8
|
4
|
229,8
|
-92,0
|
33870,7
|
|
180,8-244,7
|
5
|
233,5
|
-88,3
|
39019,8
|
|
244,7-308,5
|
7
|
285,2
|
-36,6
|
9378,6
|
|
308,5-372,3
|
9
|
288,5
|
-33,3
|
9966,3
|
|
372,3-436,2
|
11
|
363,6
|
41,7
|
19155,3
|
|
436,2-500,0
|
4
|
427,5
|
105,6
|
44630,8
|
|
Всего
|
40
|
|
|
156021,6
|
Расчет
межгрупповой дисперсии 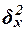 по формуле (11):
по формуле (11):
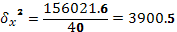
Расчет эмпирического коэффициента детерминации 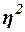 по формуле (9):
по формуле (9):
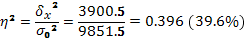
Вывод.
39.6% вариации цены 1 кв. м.
общей площади квартир обусловлено вариацией рейтинга районов по отдаленности от
центра города, а 60,4% – влиянием прочих
неучтенных факторов.
Эмпирическое
корреляционное отношение 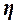 оценивает
тесноту связи между факторным и результативным признаками и вычисляется по
формуле
оценивает
тесноту связи между факторным и результативным признаками и вычисляется по
формуле
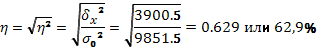
Значение
показателя изменяются в пределах 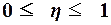 . Чем ближе значение
. Чем ближе значение 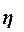 к 1, тем теснее
связь между признаками. Для качественной оценки тесноты связи на основе
к 1, тем теснее
связь между признаками. Для качественной оценки тесноты связи на основе 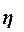 служит шкала
Чэддока (табл. 14):
служит шкала
Чэддока (табл. 14):
Таблица 14
Шкала Чэддока
|
h
|
0,1 – 0,3
|
0,3 – 0,5
|
0,5 – 0,7
|
0,7 – 0,9
|
0,9 – 0,99
|
|
Характеристика
силы связи
|
Слабая
|
Умеренная
|
Заметная
|
Тесная
|
Весьма тесная
|
Вывод.
Согласно шкале Чэддока связь между рейтингом районов и ценой квартир заметная.
Задание 3
По результатам выполнения
Задания 1 с вероятностью 0,997 необходимо определить:
1)
ошибку
выборки средней цены 1 кв. м
общей площади однокомнатной квартиры и границы, в которых будет находиться
средняя цена 1 кв. м
общей площади однокомнатной квартиры в генеральной совокупности
2)
ошибку выборки
дои квартир со средней ценой 1 кв. м общей площади 308,5 у.е. и более и
границы, в которых будет находиться генеральная доля.
Выполнение Задания
3
Целью
выполнения данного Задания является определение для генеральной
совокупности районов города региона границ, в которых будут находиться величина
средней цены 1 кв. м
общей площади однокомнатной квартиры и доля районов, в которых цена 1 кв. м общей площади
однокомнатной квартиры не менее 308,5 у.е. за 1 кв. м.
1. Определение ошибки выборки для величины
среднесписочной численности менеджеров, а также границ, в которых будет
находиться генеральная средняя
Применяя
выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки
репрезентативности), т.к. генеральные и выборочные харак- теристики, как
правило, не совпадают, а отклоняются на некоторую величину ε.
Принято
вычислять два вида ошибок выборки - среднюю 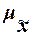 и предельную
и предельную
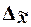 .
.
Для расчета средней ошибки выборки 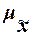 применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
Для собственно-случайной
и механической выборки с бесповторным способом отбора средняя
ошибка 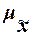 для выборочной средней
для выборочной средней 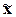 определяется по
формуле
определяется по
формуле
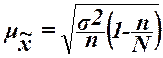 ,
,
где 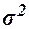 – общая
дисперсия изучаемого признака,
– общая
дисперсия изучаемого признака,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная ошибка выборки 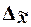 определяет границы, в пределах которых
будет находиться генеральная средняя:
определяет границы, в пределах которых
будет находиться генеральная средняя:
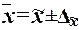 ,
,
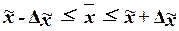 ,
,
где 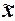 – выборочная средняя,
– выборочная средняя,
 – генеральная
средняя.
– генеральная
средняя.
Предельная
ошибка выборки  кратна средней
ошибке
кратна средней
ошибке 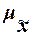 с коэффициентом
кратности t
(называемым также коэффициентом
доверия):
с коэффициентом
кратности t
(называемым также коэффициентом
доверия):
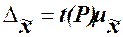
Коэффициент
кратности t зависит от значения
доверительной вероятности Р, гарантирующей вхождение
генеральной средней в интервал 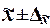 , называемый доверительным интервалом.
, называемый доверительным интервалом.
Наиболее
часто используемые доверительные вероятности Р и соответствующие им
значения t задаются следующим образом (табл.
14):
Таблица 14
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По
условию Задания 2 выборочная совокупность насчитывает 40 районов, выборка 30%
механическая, следовательно, генеральная совокупность включает 134 района.
Выборочная средняя 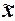 , дисперсия
, дисперсия 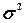 определены в
Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 15:
определены в
Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 15:
Таблица 15
|
Р
|
t
|
n
|
N
|
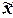
|
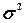
|
|
0,954
|
3
|
40
|
134
|
304,7
|
7869,6
|
Рассчитаем
среднюю ошибку выборки:
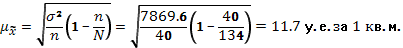
Рассчитаем
предельную ошибку выборки:
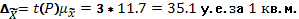
Определим доверительный интервал
для генеральной средней:
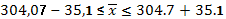
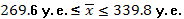
Вывод. На основании проведенного
выборочного обследования с вероятностью 0,997 можно утверждать, что для
генеральной совокупности районов средняя цена 1 кв. м. общей площади
однокомнатной квартиры находится в
пределах от 269,6 до 339,8 у.е.
2. Определение ошибки выборки для доли фирм со среднесписочной
численностью менеджеров 40 человек и
более, а также границ, в которых будет находиться генеральная доля
Доля единиц
выборочной совокупности, обладающих тем или иным заданным свойством, выражается
формулой
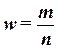 ,
,
где m – число единиц совокупности, обладающих заданным
свойством;
n – общее число единиц в совокупности.
Для собственно-случайной
и механической выборки с бесповторным способом отбора предельная
ошибка выборки 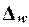 доли единиц,
обладающих заданным свойством, рассчитывается по формуле
доли единиц,
обладающих заданным свойством, рассчитывается по формуле
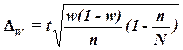 ,
,
где w – доля единиц совокупности, обладающих заданным
свойством;
(1-w) – доля единиц совокупности,
не обладающих заданным свойством,
N – число единиц в
генеральной совокупности,
n– число единиц в
выборочной совокупности.
Предельная ошибка выборки 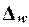 определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
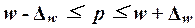
По условию
Задания 3 исследуемым свойством фирм является равенство или превышение
среднесписочной численности менеджеров величины 40 человек.
Число фирм с
данным свойством определяется из табл. 3 (графа 3):
m=24
Рассчитаем
выборочную долю:
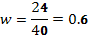
Рассчитаем
предельную ошибку выборки для доли:
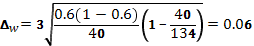
Определим
доверительный интервал генеральной доли:
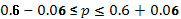
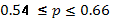
Или 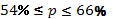
Вывод. С
вероятностью 0,997 можно утверждать, что в генеральной совокупности районов
доля районов с ценой 1 кв. м. общей площади
однокомнатной квартиры 308,5 у.е. и более будет находиться в пределах от 54% до
66%.
Задание 4
Имеются
следующие данные об обороте розничной торговли на вещевых, смешанных и продовольственных
рынках городов региона:
|
Город
|
Объем продаж в текущих ценах, млн.руб.
|
2-й год в % к
1-му году 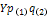
|
3-й год в % ко
2-му году 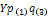
|
|
1-й год 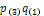
|
3-й год 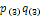
|
в сопоставимых ценах (ценах 1-го года)
|
|
1
|
1906,2
|
2319,9
|
109,0
|
115,0
|
|
2
|
42,8
|
49,7
|
103,0
|
103,0
|
|
3
|
369,3
|
495,6
|
120,0
|
112,0
|
|
4
|
11,6
|
12,2
|
94,0
|
107,0
|
|
5
|
606,0
|
672,2
|
99,0
|
82,0
|
|
сумма
|
2935,9
|
3549,6
|
|
|
По каждому
городу и для всех городов вместе вычислите базисные (к 1-му году) индексы:
·
оборота розничной торговли в текущих ценах;
·
оборота розничной торговли в сопоставимых ценах;
·
цен;
·
абсолютные просты оборота розничной торговли за
счет изменения физического объема продаж товаров, за счет изменения цен на
товары.
Сделайте
выводы.
Решение
задания 4.
Используемы
формулы:
Индекс
товарооборота в текущих ценах
Индекс
товарооборота в сопоставимых ценах
Индекс
цен
Абсолютные
приросты оборота розничной торговли за счет изменения фактического объема 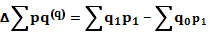
Абсолютные
приросты оборота розничной торговли за счет изменения цен на товары 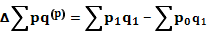
Расчет
показателей для первого города:

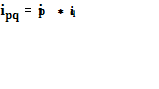
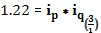
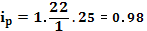


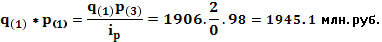
товарооборот в 1-м году по ценам 1-ого года.
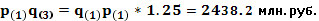
Товарооборот
3-его года в ценах 1-ого года
Индекс
оборота торговли в сопоставимых ценах:

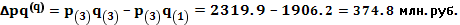
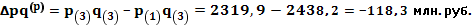
Аналогично рассчитываются
показатели по остальным городам. Результаты расчетов приведены в таблице:
|
Город
|
индекс товарооборота
|
абсолютный прирост оборота, млн. руб
|
Товарооборот 1-ого года в ценах 1-ого
года, млн. руб.
|
индекс цен
|
Товарооборот 3-его года в
ценах 1-ого года, млн. руб.
|
|
в текущих ценах
|
в сопоставимых
ценах
|
за счет
изменения объема продаж
|
за счет
изменения цены
|
|
1
|
1,2
|
1,3
|
413,7
|
-118,3
|
1945,1
|
0,98
|
2438,2
|
|
2
|
1,2
|
1,1
|
6,9
|
8,2
|
39,1
|
1,09
|
41,5
|
|
3
|
1,3
|
1,3
|
126,3
|
-1,5
|
369,9
|
1,00
|
497,1
|
|
4
|
1,1
|
1,0
|
0,6
|
1,0
|
11,1
|
1,05
|
11,2
|
|
5
|
1,1
|
0,8
|
66,2
|
312,2
|
443,5
|
1,37
|
360,0
|
|
по всем
|
1,2
|
1,2
|
613,7
|
201,7
|
2808,7
|
0,98
|
3347,9
|
Вывод:
Результаты проведенного исследования показали, что товарооборот в текущих ценах
по городу 1 (2; 3; 4; 5; по всем вместе)увеличился на 20% (20%; 30%; 10%; 10%;
20%), в сопоставимых ценах (ценах 1-ого года) товарооборот по городам 1, 2, 3,
4, и по всем вместе увеличился на 30%, 10%, 30%, 0% и 20% соответственно, а по
городу 4 сократился на 20%. Цены на товары по городу 1 и по всем городам вместе
сократились на %, а по городам 2, 3, 4, 5 увеличились на 9%, 0%, 5% и 37%.
Абсолютный прирост оборота за счет изменения цены в городах 1 и 3 составил -118,3 и -1,5 млн.
руб., а в городах 2, 5 и по всем городам вместе увеличился на 8,2, 312,2 и
201,7 млн. руб; в городе 4 оборот не изменился. Абсолютный прирост оборота за
счет изменения фактического объема продаж в городах 1, 2, 3, 4, 5 и во всех
городах вместе увеличился соответственно на 413,7, 6,9, 126,3, 0,6, 66,2 и
613,7 млн. руб.
[1] Если в
дискретном ряду все варианты встречаются одинаково часто, то в этом случае мода
отсутствует. Могут быть распределения, где не один, а два (или более) варианта
имеют наибольшие частоты. Тогда ряд имеет две (или более) моды, распределение
является бимодальным (или многомодальным),что указывает на качественную
неоднородность совокупности по изучаемому признаку.