Задача 1.
 1.6. Финансовый консультант фирмы «АВС» консультирует клиента
по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не
более 25000$) в два наименования акций крупных предприятий в составе холдинга
«Дикси».
1.6. Финансовый консультант фирмы «АВС» консультирует клиента
по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не
более 25000$) в два наименования акций крупных предприятий в составе холдинга
«Дикси».
Анализируются акции «Дикси –
Е» и «Дикси – В». Цены на акции: «Дикси – Е» - 5$ за акцию; «Дикси –В» - 3$ за
акцию.
Клиент уточнил, что он хочет
приобрести максимум 6000 акций обоих наименований, при этом акций одного
наименования должно быть не более 5000 штук.
По оценкам «АВС» прибыль от
инвестиций в эти две акции в следующем году составит: «Дикси – Е» - 1,1$;
«Дикси – В» - 0,9$.
Задача консультанта состоит в
том, чтобы выдать клиенту рекомендации по оптимизации прибыли от инвестиций.
Построить экономико-математическую модель задачи, дать необходимые комментарии
к ее элементам и получить решение графическим методом. Что произойдет, если
решать задачу на минимум и почему?
Решение
Пусть X1 – кол-во акций
«Дикси-Е»,
X2 – кол-во акций «Дикси-В».
Тогда
стоимость акций будет задаваться целевой функцией:
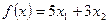
|
Вид дохода
|
Наименования акций
|
Запас средств
|
|
Дикси-Е
|
Дикси-В
|
|
Стоимость 1 акции
|
5
|
3
|
25000
|
|
Прибыль от инвестиции акций в следующем году
|
1,1
|
0,9
|
|
|
Рекомендации
|
Х1
|
Х2
|
|
Экономико-математическая
модель задачи имеет вид:
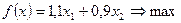
Ограничения
по необходимому максимуму кол-ва акций:
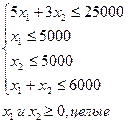
Для получения решения графическим методом строим
прямые:
8000
7000
6000
5000
4000
3000
2000
1000
О
|
|
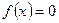
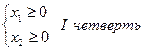
Решением
является замкнутый многоугольник ОАВС любая точка этого многоугольника внутри и
на границе является решением или рекомендацией допустимой задачи.
Чтобы из
бесконечности множества возможных рекомендаций найти ту или те которые
достаточны для функции цели max значение.
Надо найти
расположение всех точек в которых функция цели принимает одно какое-нибудь
определенное значение, т.е. строим линию равных значений (линия уровня)  , все линии уровня параллельны между собой поэтому проведем
еще одну параллельную
, все линии уровня параллельны между собой поэтому проведем
еще одну параллельную через точку (0,0).
через точку (0,0).
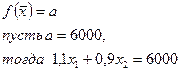
Построим
векто-градиент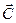 перпендикулярный линии уровня
перпендикулярный линии уровня  , и двигаться в направлении вектора-градиента до крайней
точки через которую он «покидает» многоугольник системы ограничений.
, и двигаться в направлении вектора-градиента до крайней
точки через которую он «покидает» многоугольник системы ограничений.
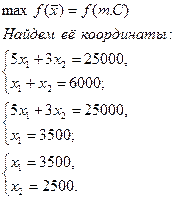
Точка С
(3500;2500)
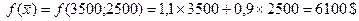
Если решать
задачу на min то надо двигаться по линии вектора-градиента в обратном
направлении линии уровня и иксы поменяют друг с другом свои значения.
Ответ:
максимальная прибыль в следующем году: 6100$
При покупке акций Дикси-Е (Х1)=3500
(шт.), Дикси-В (Х2)=2500 (шт.).
Задача 2.
2.6. На
основании информации, приведенной в таблице, решается задача оптимального
использования ресурсов на максимум выручки от реализации готовой продукции.
|
Вид сырья
|
Наименование
расхода сырья на ед. продукции
|
Запасы
сырья
|
|
А
|
Б
|
В
|
I
II
III
|
18
6
5
|
15
4
3
|
12
8
3
|
360
192
180
|
|
Цена изделия
|
9
|
10
|
16
|
|
Требуется:
1)
Сформулировать прямую оптимизационную задачу на
максимум выручки от реализации готовой продукции, получить оптимальный план
выпуска продукции.
2)
Сформулировать двойственную задачу и найти ее
оптимальный план с помощью теорем двойственности.
3)
Пояснить нулевые значения переменных в оптимальном
плане.
4)
На основе свойств двойственных оценок и теорем
двойственности:
-
проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить,
как изменяется выручка от реализации продукции и план ее выпуска, если запас
сырья I вида увеличить
на 4,5 кг,
а II – уменьшить на 9 кг;
- оценить
целесообразность включения в план изделия «Г» ценой 11 ед., на изготовление
которого расходуется 9, 4 и 6
кг соответствующего вида сырья.
Решение
1) Пусть
необходимо изготовить х1 единиц продукции A, х2 единиц продукции
Б и х3 единиц продукции В. Прямая оптимизационная задача на
максимум выручки от реализации готовой продукции имеет вид:
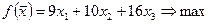
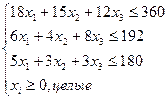
Оптимальный план выпуска
продукции будем искать с помощью настройки «Поиск решения» MS Excel.
Сначала занесем исходные данные:
|
|
A
|
B
|
C
|
D
|
E
|
F
|
|
3
|
|
X1
|
X2
|
X3
|
|
|
|
4
|
Значения переменных
|
0
|
0
|
0
|
ЦФ
|
|
|
5
|
Коэф. целевой ф-ии
|
9
|
10
|
16
|
=СУММПРОИЗВ($В$4:$D$4;В5:D5)
|
|
|
6
|
|
|
|
|
|
|
|
7
|
Ограничения
|
|
|
|
Левая часть
|
Правая часть
|
|
8
|
I
|
18
|
15
|
12
|
=СУММПРОИЗВ($В$4:$D$4;В8:D8)
|
360
|
|
9
|
II
|
6
|
4
|
8
|
=СУММПРОИЗВ($В$4:$D$4;В9:D9)
|
192
|
|
10
|
III
|
5
|
3
|
3
|
=СУММПРОИЗВ($В$4:$D$4;В10:D10)
|
180
|
Теперь будем искать
оптимальное решение с помощью настройки «Поиск решения»:
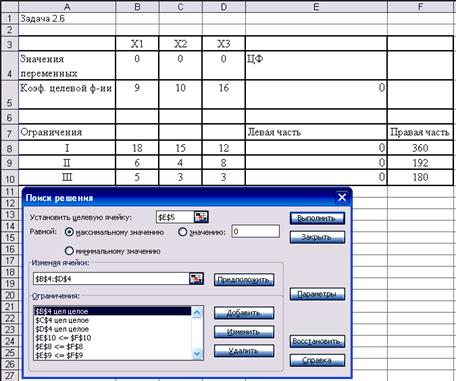
В результате будет получена следующая таблица:
|
2
|
A
|
B
|
C
|
D
|
E
|
F
|
|
3
|
|
X1
|
X2
|
X3
|
|
|
|
4
|
Значения переменных
|
0
|
8
|
20
|
ЦФ
|
|
|
5
|
Коэф. целевой ф-ии
|
9
|
10
|
16
|
400
|
|
|
6
|
|
|
|
|
|
|
|
7
|
Ограничения
|
|
|
|
Левая часть
|
Правая часть
|
|
8
|
I
|
18
|
15
|
12
|
360
|
360
|
|
9
|
II
|
6
|
4
|
8
|
192
|
192
|
|
10
|
III
|
5
|
3
|
3
|
84
|
180
|
Таким образом, чтобы получить максимум выручки в размере
400 ден.ед. необходимо изготовить 0 единиц продукции А, 8 единицы продукции Б и
20 единиц продукции В.
2) Строим двойственную задачу в виде:
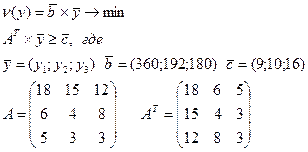
Запишем двойственную задачу:
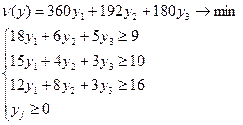
Найдем решение
двойственной задачи с
помощью теорем двойственности. Проверим выполнение системы
неравенств прямой задачи:
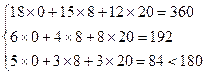
Так как третье неравенство
выполняется как строгое, то у3 = 0
Так как х2 ≠
0 и х3 ≠ 0, то получаем систему уравнений:
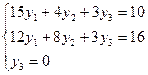
Решение системы: y1=2/9, y2=5/3, y3=0.
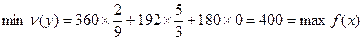
3) В прямой
задаче Х1=0, так как при достаточно высоких
затратах производство продукции I приносит небольшую прибыль.
В двойственной задаче у3=0, так как III вид сырья является
избыточным и не расходуется полностью на производство продукции.
4) а) Наиболее дефицитным
является II вид сырья,
так как его двойственная оценка (у2 = 5/3) является
наибольшей.
б) При увеличении запасов сырья I вида на 45 кг. и уменьшении запасов
сырья II вида на 9 кг. изменение выручки
составит:
2/9*45–5/3*9 = -5 ден.ед.
И она будет равна: 400-5 = 395
ден.ед.
Определим изменение плана
выпуска аз системы уравнений:
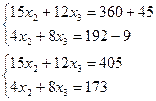
То есть оптимальный план выпуска будет иметь вид:
X1=0 X2=11 X3=20 max f(x) = 395
(ден.ед)
в) оценим целесообразность включения в план изделия Г вида
ценой 11ед., если нормы затрат сырья 9, 4 и 6 кг.
Затраты на изготовление единицы изделия Г составят:
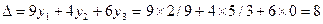
Так как затраты на производство изделия меньше, чем его
стоимость (∆ = 8 < 11), то включение в план изделия Г целесообразно,
так как оно принесет дополнительную прибыль.
Ответ:  =400 ден.ед, включение в план изделия Г целесообразно.
=400 ден.ед, включение в план изделия Г целесообразно.
Задача 4.
Задача 4.6. В течение девяти
последовательных недель фиксировался спрос Y(t)
(млн. р.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя (повариантно)
приведен ниже в таблице
|
Номер варианта
|
Номер наблюдения (t=1,2,...,9)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
6
|
12
|
15
|
16
|
19
|
17
|
20
|
24
|
25
|
28
|
Требуется:
1)
Проверить наличие аномальных наблюдений.
2)
Построить линейную модель Ŷ(t)=a0 +a1
t, параметры
которой оценить МНК (Ŷ(t)
– расчетные, смоделированные значения временного ряда).
3)
Построить адаптивную модель Брауна Ŷ(t)=a0 +a1 k с параметром сглаживания α=0,4 и
α=0,7; выбрать лучшее значение параметра сглаживания α.
4)
Оценить адекватность построенных моделей, используя
свойства независимости остаточной компоненты, случайности и соответствия
нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7 – 3,7).
5)
Оценить точность моделей на основе использования
средней относительной ошибки аппроксимации.
6)
По двум построенным моделям осуществить прогноз спроса
на следующие две недели (доверительный интервал прогноза при доверительной
вероятности p=70%).
7)
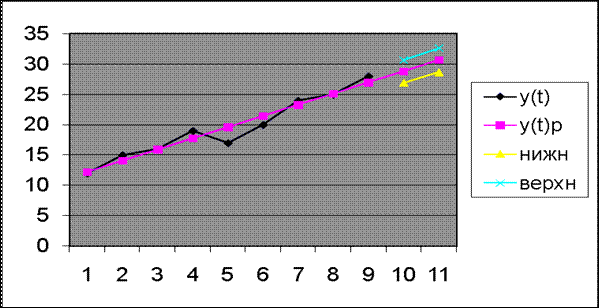
Фактические значения показателя, результаты
моделирования и прогнозирования представить графически.
Вычисления провести с одним знаком в
дробной части. Основные промежуточные результаты вычислений представить в
таблицах (при использовании компьютера представить соответствующие листинги с
комментариями).
Решение
1) Методом Ирвина проверим анамальность ряда, где λ должна быть ≥1,6
для нормального ряда.
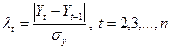
где среднеквадратическое отклонение
рассчитывается с использованием формул:
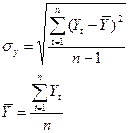
Построим следующий ряд:
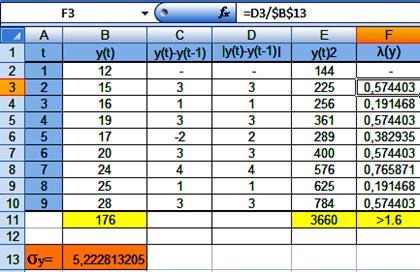
y(t)2=B2^2
λ(y) =D3/$B$13
σy=((9*E11-B11^2)/72)^0,5
Анамальных наблюдений во временном
ряду нет.
2) Построим линейную модель вида Yр(t) = a0 + a1t
Параметры а0 и а1 можно
найти методом наименьших квадратов из системы нормальных уравнений:
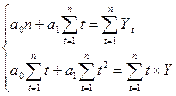
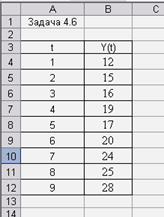
А также с использованием настройки MS Excel «Анализ данных». Для
этого занесем исходные данные в таблицу:
Затем используя пункт Регрессия настройки - «Анализ
данных»

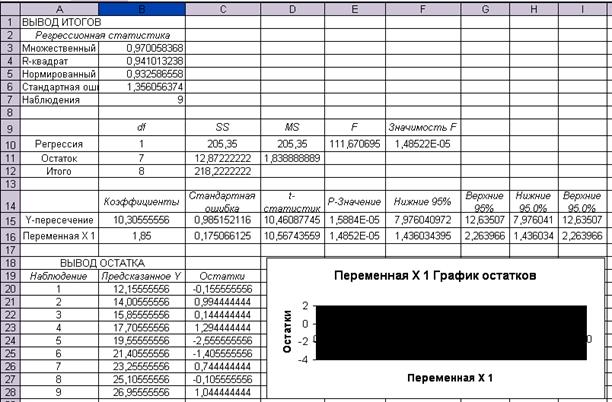
Средствами MS Excel
получена следующая линейная модель: Yp(t) = 1,85 t + 10,30
Построим
график эмпирического и смоделированного рядов:
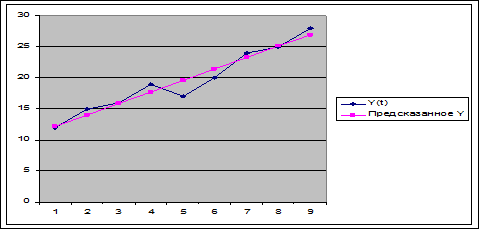
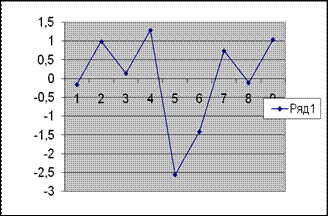

3) Это значение сравнивается с фактическим уровнем
и полученная ошибка прогноза:
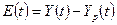
используется
для корректировки модели.
Корректировка параметров
осуществляется по формулам:
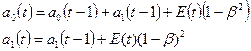
а) Примем а = 0,4, тогда 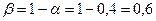 В качестве
начальных параметров модели возьмем, исчисленные в линейной модели: а0
= 11,6; а1 = 1,4.
В качестве
начальных параметров модели возьмем, исчисленные в линейной модели: а0
= 11,6; а1 = 1,4.
Расчет проведем с помощью MS Excel в результате получим
следующую таблицу:
|
t
|
y(t)
|
ao(t)
|
a1(t)
|
yp(t)
|
e(t)
|
|
0
|
|
11,6
|
1,4
|
|
|
|
1
|
12
|
12,09
|
0,76
|
13
|
-1
|
|
2
|
15
|
14,226
|
2,7165
|
12,85
|
2,15
|
|
3
|
16
|
16,08483
|
1,858825
|
16,9425
|
-0,9425
|
|
4
|
19
|
18,90493
|
2,820104
|
17,94365
|
1,05635
|
|
5
|
17
|
17,42525
|
-1,47968
|
21,72503
|
-4,72503
|
|
6
|
20
|
19,6351
|
2,209849
|
15,94558
|
4,054423
|
|
7
|
24
|
23,80605
|
4,170944
|
21,84495
|
2,155049
|
|
8
|
25
|
25,26793
|
1,461883
|
27,97699
|
-2,97699
|
|
9
|
28
|
27,88568
|
2,617754
|
26,72981
|
1,270188
|
Рассчитаем среднюю ошибку аппроксимации по модели:
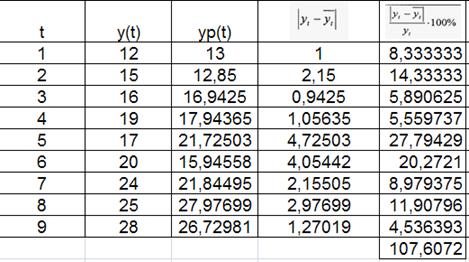
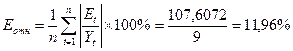
б) Примем а = 0,7, тогда
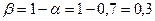 . В качестве
начальных параметров модели возьмем, исчисленные в линейной модели: а0
= 11,6; а1 = 1,4. Получим
следующую таблицу:
. В качестве
начальных параметров модели возьмем, исчисленные в линейной модели: а0
= 11,6; а1 = 1,4. Получим
следующую таблицу:
|
t
|
y(t)
|
ao(t)
|
a1(t)
|
yp(t)
|
e(t)
|
|
0
|
|
11,6
|
1,4
|
|
|
|
1
|
12
|
12,09
|
0,49
|
13
|
-1
|
|
2
|
15
|
14,7822
|
2,6922
|
12,58
|
2,42
|
|
3
|
16
|
16,1327
|
1,350496
|
17,4744
|
-1,4744
|
|
4
|
19
|
18,86349
|
2,73079128
|
17,48319
|
1,516808
|
|
5
|
17
|
17,41349
|
-1,45000221
|
21,59428
|
-4,59428
|
|
6
|
20
|
19,63671
|
2,223228387
|
15,96348
|
4,036517
|
|
7
|
24
|
23,80739
|
4,170681309
|
21,85994
|
2,140058
|
|
8
|
25
|
25,26803
|
1,460632081
|
27,97808
|
-2,97808
|
|
9
|
28
|
27,88558
|
2,617552457
|
26,72866
|
1,271341
|
Рассчитаем среднюю ошибку аппроксимации по модели:
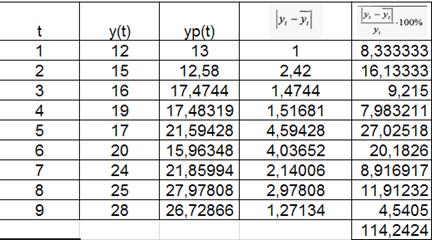
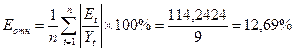
Таким образом, лучшей является модель Брауна
с параметром а =0,4.
4) Оценим адекватность построенной модели
также используя MS Excel.
Для нахождения необходимых показателей построим таблицу:
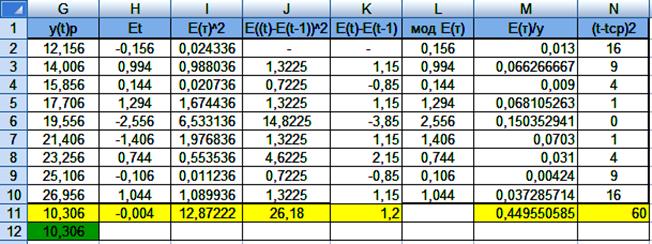
Et=B2-G2
Е(т)^2=H2^2
E((t)-E(t-1))^2=(H3-H2)^2
E(t)-E(t-1) =H3-H2
мод Е(т) =ABS(H2)
Е(т)/у=L2/B2
Так как сумма Ет =0.004 = 0 то гипотеза Но:М(е)=0
подтверждается.
·
Условие случайности отклонений от тренда.
Рассчитаем критическое число поворотных точек по формуле:

Так как для данной модели р = 6 > 2, то условие
выполнено.
·
Условие наличия (отсутствия) автокорреляции в
отклонениях. Рассчитаем статистику Дарбина-Уотсона (d- статистику) по формулам:
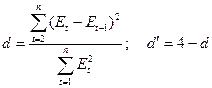
d=2,03383658
d'=4–2,03383658=1,96616342
Критические значения статистики: d1kp=1,08 и d2kp=1,36;
d и d'>1,36
поэтому уровни остатков не зависимы
·
Условие соответствия ряда остатков нормальному
закону распределения. Рассчитаем RS - критерий:
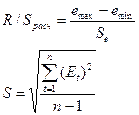
Se=((9*(I11-H11^2)/72)^0,5)=1,2685
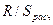 =(1,294-(-2,556))/1,2685=3,04
=(1,294-(-2,556))/1,2685=3,04
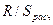
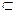 (2,7;3,7), т.е. 3,04
(2,7;3,7), т.е. 3,04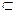 (2,7;3,7), значит модель адекватна.
(2,7;3,7), значит модель адекватна.
5) Оценим
точность построенной модели на основе относительной ошибки аппроксимации,
рассчитанной по формуле:
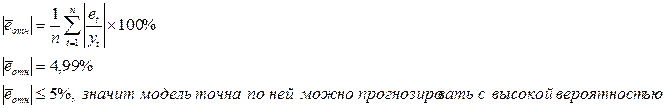
6) Строим прогноз по построенным моделям:
точечный прогноз получается путем подстановки в модель
значений времени t, соответствующих
периоду упреждения k:
t = n+k. Так, в случае трендовой модели в
виде полинома первой степени - линейной модели роста -экстраполяция на k шагов
вперед имеет вид:

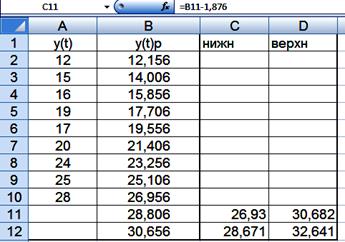
Точечный прогноз на следующие две недели имеет вид:
Yn+1=10,30+1,85(9+1)=28,806
Yn+2=10,30+1,85(9+2)=
30,656
Учитывая, что модель плохой точности будем прогнозировать
с небольшой вероятностью Р=0,7
Доверительный интервал:
Критерий Стьюдента (при доверительной вероятности
р = 0,7; ν = n-2=
9-2=7), равен: t= 1,119
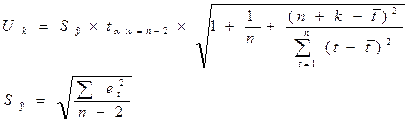
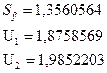
7) Представим графически результаты моделирования и
прогнозирования для этого составим таблицу: