ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА
по
дисциплине
ЭКОНОМЕТРИКА
Вариант №24
Архангельск, 2007
Таблица данных
|
Номер показателя
|
Номер наблюдения
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
15
|
20
|
24
|
30
|
33
|
37
|
36
|
40
|
42
|
|
2
|
70
|
74
|
76
|
75
|
78
|
78
|
83
|
85
|
87
|
|
3
|
82
|
79
|
78
|
72
|
69
|
70
|
64
|
61
|
59
|
Требуется:
I
1)
определить наличие тренда Y(t);
2)
построить линейную модель Y(t) = a0 + a1t, параметры которой оценить с помощью МНК;
3)
оценить адекватность
построенных моделей на основе исследования:
·
случайности остаточной
компоненты по критерию пиков;
·
независимости уровней ряда
остатков по d - критерию (в качестве критических используйте уровни d1 = 1.08 и d2 = 1,36) или по первому
коэффициенту корреляции, критический уровень которого r(1) = 0,36;
·
нормальности распределения
остаточной компоненты по R/S -
критерию с критическими уровнями 2,7 – 3,7;
4)
для оценки точности модели используйте
среднеквадратическое отклонение и среднюю по модулю относительную ошибку;
5)
построить точечный и
интервальный прогнозы на два шага вперед (для вероятности P = 70% используйте коэффициент ta,n = 1.11).
II
1)
постройте матрицу
коэффициентов парной корреляции Y(t) с X1(t) и X2(t) и выбрать фактор, наиболее тесно
связанный с переменной Y(t);
2)
построить линейную
однопараметрическую модель регрессии Y(t) = a0 + a1t;
3)
оценить качество построенной
модели, исследовав ее адекватность и точность;
4)
для модели регрессии
рассчитать коэффициент эластичности и b–коэффициент;
5)
построить точечный и
интервальный прогнозы на два шага вперед по модели регрессии (для вероятности P = 70% используйте коэффициент n = 1.11). Прогнозные оценки фактора X(t) на два шага вперед получить на
основе среднего прироста от фактически достигнутого уровня.
III
Отобразить на графиках фактические данные,
результаты расчетов (I – 1, 3, 4, 6; II – 2, 5) и прогнозирования по всем моделям.
Задание I
Определяем наличие тренда Y(t).
|
t
|
yt
|
Ut
|
lt
|
St
|
dt
|
|
1
|
15
|
-
|
-
|
-
|
-
|
|
2
|
20
|
1
|
0
|
1
|
1
|
|
3
|
24
|
1
|
0
|
1
|
1
|
|
4
|
30
|
1
|
0
|
1
|
1
|
|
5
|
33
|
1
|
0
|
1
|
1
|
|
6
|
37
|
1
|
0
|
1
|
1
|
|
7
|
36
|
0
|
0
|
0
|
0
|
|
8
|
40
|
1
|
0
|
1
|
1
|
|
9
|
42
|
1
|
0
|
1
|
1
|
|
|
7
|
|
7
|
7
|
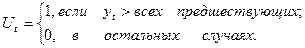
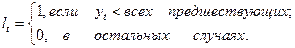
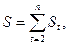 где
где 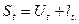 S = 7.
S = 7.
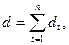 где
где 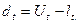 d = 7.
d = 7.
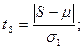
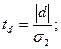
При n < 10, m = 3,858, s1 = 1,288, s2 = 1,964.
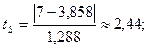
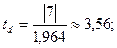
a = 0,05; n = 9.
ta;(n-2)(табл) = t(a=0,05;8) = 2,36,
tS > ta;(n-2)(табл), тенденция в дисперсии
есть.
td > ta;(n-2)(табл), тренд есть.
1)
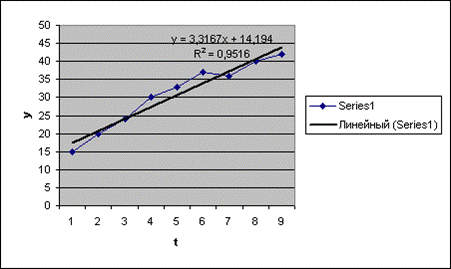
Строим линейную модель Y(t) = a0 + a1t, параметры которой оценим с помощью МНК.
|
t
|
Yt
|
t^2
|
Yt расч
|
Et
|
m
|
Et^2
|
(Et-Et-1)^2
|
|
|
|
1
|
15
|
1
|
17,5
|
-2,5
|
-
|
6,25
|
|
|
|
2
|
20
|
4
|
20,8
|
-0,8
|
0
|
0,64
|
2,89
|
|
|
3
|
24
|
9
|
24,1
|
-0,1
|
0
|
0,01
|
0,49
|
|
|
4
|
30
|
16
|
27,4
|
2,6
|
1
|
6,76
|
7,29
|
|
|
5
|
33
|
25
|
30,7
|
2,3
|
1
|
5,29
|
0,09
|
|
|
6
|
37
|
36
|
34
|
3
|
1
|
9
|
0,49
|
|
|
7
|
36
|
49
|
37,3
|
-1,3
|
1
|
1,69
|
18,49
|
|
|
8
|
40
|
64
|
40,6
|
-0,6
|
1
|
0,36
|
0,49
|
|
|
9
|
42
|
81
|
43,9
|
-1,9
|
-
|
3,61
|
1,69
|
|
|
45
|
277
|
285
|
276,3
|
0,7
|
5
|
33,61
|
31,92
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
|
Y-пересечение
|
14,2
|
|
t
|
3,3
|
a0 = 14,2 a1 = 3,3.
Yрасч(t) =14,2 + 3,3*t – линейное уравнение трендовой модели
2)
Оцениваем адекватность
построенной модели.
Проверяем свойства остатков:
а) Случайность значений остатков (критерий
поворотных точек или пиков).
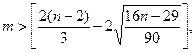 где m – количество поворотных точек или пиков.
где m – количество поворотных точек или пиков.
m = 5,
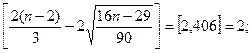
5>2, неравенство выполняется, ряд остатков можно
считать случайными, т.е. он не содержит регулярную компоненту.
б) Проверяем отсутствие автокорреляции или
независимость значений остатков ( критерий Дарвина-Уотсона).
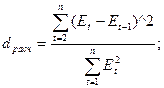
dрасч = 0,95,
d1 =
1,08,
d2 =
1,36,
dрасч < d1 , то свойство не выполняется, остатки зависимы, автокорреляция есть
в) Нормальный закон распределения остатков
(R/S-критерий).
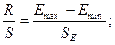
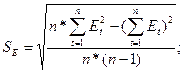
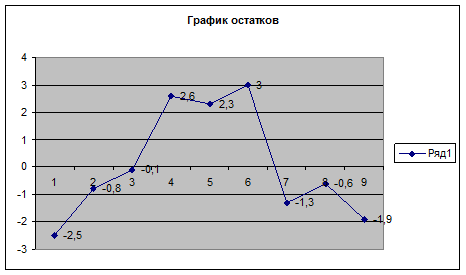
Emax
=3,0, Emin
= -2,5, SE = 2,048.
R/S =2,76 . (2,7 – 3,7).
2,7 < 2,76< 3,7,
свойство выполняется, гипотеза о нормальном распределении ряда остатков
принимается.
Модель адекватна с вероятностью 0,95, т.к. рядом остатков выполняются все
свойства.
3)
Оцениваем
точность модели (используя среднеквадратическое отклонение и среднюю по модулю
относительную ошибку).
а) Стандартная ошибка отклонений:
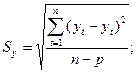
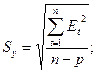
Sy = 2,19.
б) Средний модуль остатков:
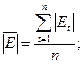
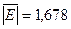
в) Средняя относительная ошибка аппроксимации:
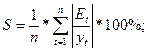
S = 6,05 %,
5% < S <
10%, модель приемлема для анализа.
в) Проверка равенства (М/Е)=0
tp=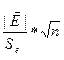
tp=2,35
t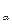 (0,01;8)=3,36
(0,01;8)=3,36
2,35<3,36, свойство выполняется, следовательно
модель адекватна с вероятностью 0,99
4)
Строим точечный и
интервальный прогнозы на два шага вперед (для вероятности P = 70% используйте коэффициент ta,n = 1.11).
Точечный прогноз:
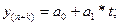
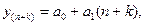 где n – количество наблюдений, k – период
упреждения (прогноза).
где n – количество наблюдений, k – период
упреждения (прогноза).
Интервальный прогноз:
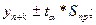
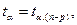 где (n – p) – число степеней свободы.
где (n – p) – число степеней свободы.
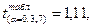
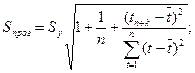
t(n+k) = n + k.
а) n
= 9, k = 1.
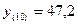 – точечный прогноз.
– точечный прогноз.
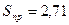

Нижняя граница – 44,192
Верхняя граница – 50,208.
(44,192 – 50,208) – интервальный прогноз.
б) n
= 9, k = 2.
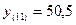 – точечный прогноз.
– точечный прогноз.
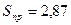
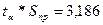
Нижняя граница – 47,314,
Верхняя граница – 53,686.
(47,314 – 53,686) – интервальный прогноз.
Задание II
1) Строим матрицу коэффициентов парной корреляции Y(t) с X1(t) и X2(t) и выбрать
фактор, наиболее тесно связанный с переменной Y(t).
|
t
|
y(t)
|
x1
|
x2
|
|
1
|
15
|
70
|
82
|
|
2
|
20
|
74
|
79
|
|
3
|
24
|
76
|
78
|
|
4
|
30
|
75
|
72
|
|
5
|
33
|
78
|
69
|
|
6
|
37
|
78
|
70
|
|
7
|
36
|
83
|
64
|
|
8
|
40
|
85
|
61
|
|
9
|
42
|
87
|
59
|
|
|
y(t)
|
x1
|
x2
|
|
y(t)
|
1
|
|
|
|
x1
|
0,912
|
1
|
|
|
x2
|
-0,960
|
-0,963
|
1
|
r (y,x1) = 0,912, связь тесная и прямая.
r (y,x2) = -0,960, связь тесная и обратная.
r (х1,x2) = -0,963 связь тесная и обратная,
0,963 > 0,8, факторы коллинеарные, т.е. линейно
зависимы, включать в модель вместе нельзя.
Проверка значимости коэффициентов
парной корреляции по критерию
Стьюдента.
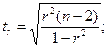
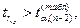 то ryx – значим.
то ryx – значим.
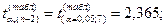
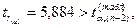
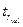 – значим, т.е. связь
между переменными y и x1 существует.
– значим, т.е. связь
между переменными y и x1 существует.
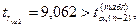
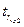 – значим, т.е. связь
между переменными y и x2 существует.
– значим, т.е. связь
между переменными y и x2 существует.
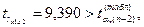
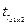 – значим, т.е. связь
между переменными x1 и x2 существует.
– значим, т.е. связь
между переменными x1 и x2 существует.
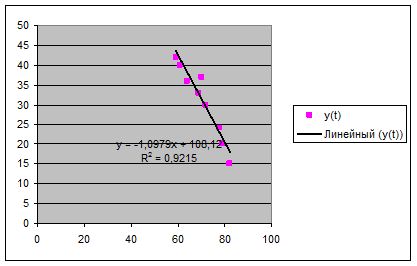
Для построения модели выбираем фактор х2,
т.к. 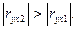
Yрасч = F(x2).
Фактор х2 обозначим через Х.
Yрасч(Х) = а0+а1*Х.
2) Строим линейную однопараметрическую модель регрессии Y(t) = a0 + a1t.
|
t
|
Хt
|
yt
|
Х^2
|
Х*У
|
У^2
|
|
1
|
82
|
15
|
6724
|
1230
|
225
|
|
2
|
79
|
20
|
6241
|
1580
|
400
|
|
3
|
78
|
24
|
6084
|
1872
|
576
|
|
4
|
72
|
30
|
5184
|
2160
|
900
|
|
5
|
69
|
33
|
4761
|
2277
|
1089
|
|
6
|
70
|
37
|
4900
|
2590
|
1369
|
|
7
|
64
|
36
|
4096
|
2304
|
1296
|
|
8
|
61
|
40
|
3721
|
2440
|
1600
|
|
9
|
59
|
42
|
3481
|
2478
|
1764
|
|
итого
|
634
|
277
|
45192
|
18931
|
9219
|
n*a0+(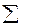 Х)*а1=
Х)*а1=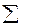 у
у
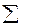 Х*а0+(
Х*а0+(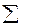 Х
Х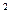 )*а1=
)*а1=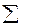 (Х*У)
(Х*У)
9*а0 +634*а1=277 *634
634*а0+45192*а1=18931 *9
5706 *а0+401956*а1=175618
5706*а0+406728*а1=170379
-4772*а1=5239
а1=-1,0979
9*а0+634*(-1,0979)=277
а0= 108,12
y = -1,0979x + 108,12-уравнение парной регрессии
а1=-1,1 показывет % изменение результата У, если один из факторов увеличить на 1% , то
есть если У увеличить на 1%, то Х уменьшится на 1,1
а)Оценка качества модели регрессии
ryх=а1*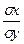

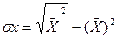 =
=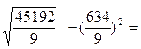 7,675
7,675
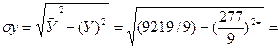 8,778
8,778
rух =-1,1*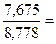 -0,962
-0,962
rух <0,
следовательно, связь обратная и очень тесная (Х увеличивается, а У уменьшается)
r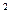 ух =0,925 или 92,5 % вариации У происходит за счет
фактора Х, включенного в модель.
ух =0,925 или 92,5 % вариации У происходит за счет
фактора Х, включенного в модель.
б) Проверяем значимость уравнения регрессии по
критерию Фишера (дисперсионный анализ).
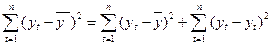 ;
;
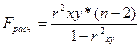 ;
;
F расч=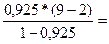 86,33
86,33
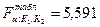 , К1 = m, К2
= n-m-1.
, К1 = m, К2
= n-m-1.
К1=1
К2=9-1-1=7
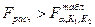 , т.е. уравнение регрессии значимо, то есть адекватно
, т.е. уравнение регрессии значимо, то есть адекватно
в) Проверяем значимость параметров уравнения
регрессии (критерий Стьюдента).
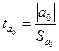 ;
;
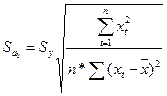 ;
;
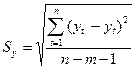 , m – количество факторов в модели.
, m – количество факторов в модели.
|
y(t)
|
x
|
у расч
|
(х-хср)^2
|
(у-уср)^2
|
(Х)^2
|
|
Еt
|
|
|Et|
|
|
Еt^2
|
|
IEtYtI
|
|
|
15
|
82
|
17,9
|
133,63
|
248,69
|
6724
|
|
-2,9
|
|
2,9
|
|
8,41
|
|
0,19
|
|
|
20
|
79
|
21,2
|
73,27
|
115,99
|
6241
|
|
-1,2
|
|
1,2
|
|
1,44
|
|
0,06
|
|
|
24
|
78
|
22,3
|
57,15
|
45,83
|
6084
|
|
1,7
|
|
1,7
|
|
2,89
|
|
0,07
|
|
|
30
|
72
|
28,9
|
2,43
|
0,59
|
5184
|
|
1,1
|
|
1,1
|
|
1,21
|
|
0,04
|
|
|
33
|
69
|
32,2
|
2,07
|
4,97
|
4761
|
|
0,8
|
|
0,8
|
|
0,64
|
|
0,02
|
|
|
37
|
70
|
31,1
|
0,19
|
38,81
|
4900
|
|
5,9
|
|
5,9
|
|
34,81
|
|
0,16
|
|
|
36
|
64
|
37,7
|
41,47
|
27,35
|
4096
|
|
-1,7
|
|
1,7
|
|
2,89
|
|
10,05
|
|
|
40
|
61
|
41,0
|
89,11
|
85,19
|
3721
|
|
-1,0
|
|
1,0
|
|
1,00
|
|
0,03
|
|
|
42
|
59
|
43,2
|
130,87
|
126,11
|
3481
|
|
-1,2
|
|
1,2
|
|
1,44
|
|
0,03
|
|
|
277
|
634
|
|
530,19
|
693,53
|
45192
|
|
1,5
|
|
17,5
|
|
54,73
|
|
0,65
|
|
уср=277/8=30,77
хср=634/9=70,44
У1 расч=108,1-1,1*82=17,9
У2
расч=108,1-1,1*79=21,2 и т.д.
Sу=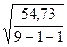 =2,796
=2,796
Sa0=2,796*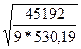 =8,6
=8,6
ta0=108,1/8,6=12,6
 ;
;
ta0>t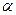 , следовательно параметр a0 значим
, следовательно параметр a0 значим
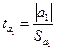 ;
;
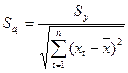 ;
;
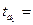 2,796
2,796
Sa1=2,796/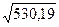 =0,12
=0,12
ta1=(-1,1)/0,12=9,2
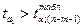 , параметр a1 значим.
, параметр a1 значим.
Интервальная оценка параметров:
a0: 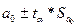 , 108,1
, 108,1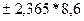
a1: 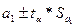 , -1,1
, -1,1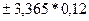
a0 =87,8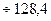 значим, т.к. 0 не
входит в интервал.
значим, т.к. 0 не
входит в интервал.
a1 =-1,4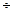 -0,8, значим, т.к. 0 не входит в интервал.
-0,8, значим, т.к. 0 не входит в интервал.
3. Оценка
качества модели (адекватность и точность)
1) Точность модели.
Стандартная ошибка отклонений:
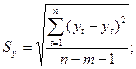
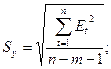
Sy ==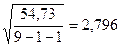 .
.
Средний модуль остатков:
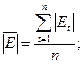
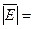 17,5/9=1,944
17,5/9=1,944
Средняя относительная ошибка аппроксимации:
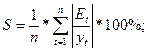
S = (1/9)*0,65=7,2%,
S < 10% , модель считается точной
2)
Проверка модели на адекватность:
а)
случайность значений остатков- критерий поворотных точек
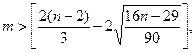
m = 5,
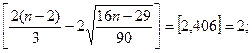
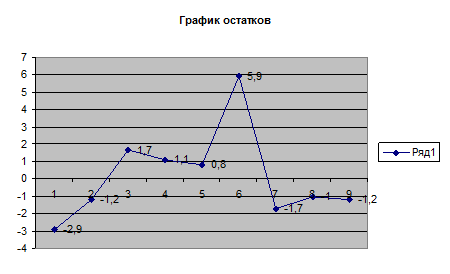
5>2, неравенство выполняется, ряд остатков можно считать случайными
б) Отсутствие автокорреляции в ряду остатков (критерий Дарбина –Уотсона)
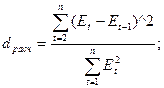
d1 =
1,08,
d2 =
1,36,
|
Еt
|
m
|
(Et-Et-1)^2
|
Еt^2
|
|
-2,9
|
-
|
-
|
8,41
|
|
-1,2
|
0
|
2,89
|
1,44
|
|
1,7
|
1
|
8,41
|
2,89
|
|
1,1
|
0
|
0,36
|
1,21
|
|
0,8
|
1
|
0,09
|
0,64
|
|
5,9
|
1
|
26,01
|
34,81
|
|
-1,7
|
1
|
57,76
|
2,89
|
|
-1,0
|
1
|
0,49
|
1,00
|
|
-1,2
|
-
|
0,04
|
1,44
|
|
1,5
|
5
|
96,05
|
54,73
|
d расч=96,05/54,73=1,75
1,36< 1,75<2, то свойство выполняется, остатки
независимы, автокорреляции нет
в) Нормальный закон распределения остатков (R/S-критерий).
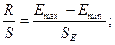
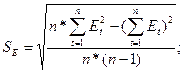
Emax
=5,9 , Emin
= -2,9,
SE = 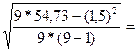 2,61
2,61
R/S =(5,9+2,9)/2,61=3,37
2,5 < 3,37< 3,9,
свойство выполняется, гипотеза о нормальном распределении ряда остатков
принимается.
г)Проверка равенства
(М(Е)=0)
tp=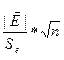
tp=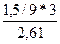 =0,19
=0,19
t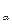 (0,05;8)= 2,36
(0,05;8)= 2,36
0,19<2,36,
свойство выполняется
Модель адекватна с
вероятностью 0,95, т.к. рядом остатков выполняются все свойства.
4) Для
модели регрессии рассчитаем коэффициент эластичности и b–коэффициент.
Коэффициент эластичности:
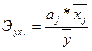 ;
;
Хср=70,44
Уср=30,77
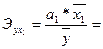
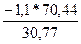 =-2,51%, или на 2,51 % в среднем уменьшится значение результативного признака y, если фактор x1 увеличить на 1 % при неизменном значении других факторов.
=-2,51%, или на 2,51 % в среднем уменьшится значение результативного признака y, если фактор x1 увеличить на 1 % при неизменном значении других факторов.
b–коэффициент:
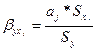 ;
;
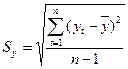 ;
;
Sy =
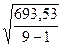 =9,31;
=9,31;
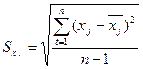 ;
;
Sх1 =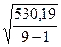 =8,14;
=8,14;
 , если фактор Х2 увеличить на 8,14, то результат Y уменьшится на 8,94
, если фактор Х2 увеличить на 8,14, то результат Y уменьшится на 8,94
5) Построим
точечный и интервальный прогнозы на два шага вперед по модели регрессии (для
вероятности P = 70%,
используйте коэффициент n = 1,11).
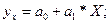
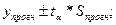
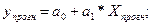
Точечный прогноз:
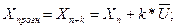 где n – количество наблюдений;
где n – количество наблюдений;
k – период упреждения;
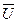 – средний абсолютный
прирост.
– средний абсолютный
прирост.
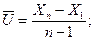

 =-2,875
=-2,875
Ширина доверительного интервала:
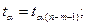
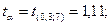
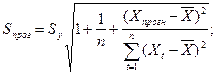
Стандартная ошибка отклонений:
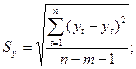
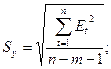
Sy = 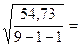 2,796.
2,796.
а) n = 9, k = 1.
Точечный прогноз:
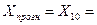 59+1*(-2,875)=56,125
59+1*(-2,875)=56,125
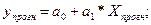
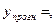 108,1-1,1*56,125=46,36 точечный прогноз.
108,1-1,1*56,125=46,36 точечный прогноз.
Ширина доверительного интервала:
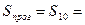 2,796*
2,796*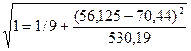 =3,42
=3,42
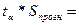 1,11*3,42=3,80
1,11*3,42=3,80
46,36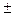 3,80
3,80
Нижняя граница – 42,56,
Верхняя граница –50,16.
(42,56 -50,16) – интервальный
прогноз.
б) n = 9, k = 2.
Точечный прогноз:
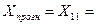 56,125+1*(-2,875)=53,25
56,125+1*(-2,875)=53,25
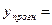 108,1-1,1*53,25= 49,53– точечный прогноз.
108,1-1,1*53,25= 49,53– точечный прогноз.
Ширина доверительного интервала:
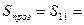 2,796*
2,796*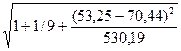 =3,61;
=3,61;
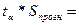 1,11*3,61=4,01
1,11*3,61=4,01
49,53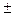 4,01
4,01
Нижняя граница –45,52,
Верхняя граница –53,54.
(45,52-53,54) – интервальный прогноз.
Дата выполнения « » марта 2007 г. Подпись ________