ЛАБОРАТОРНАЯ РАБОТА
Вариант
№5
Задание:
В задаче заданы три временных ряда: первый из
них представляет нарастающую по кварталам прибыль коммерческого банка y, второй
и третий ряд - процентные ставки этого банка по кредитованию юридических лиц x
и депозитным вкладам x2 за этот же
период.
Требуется:
1.
Вычислить матрицу
коэффициентов парной корреляции и проанализировать.
2.
Построить
линейную модель регрессии, описывающую зависимость y от факторов x1 и x2.
3.
Оценить качество
построенной модели. Вычислить для модели среднюю ошибку аппроксимации и коэффициент
детерминации.
4.
Проанализировать
влияние факторов на зависимую переменную по модели ( для каждого коэффициента регрессии
вычислить коэффициент эластичности, β-коэффициент, и ∆-коэффициент.)
и оценить их значимость при t = 1,86.
5.
Определить точные
и интервальные прогнозные оценки прибыли коммерческого банка на два квартала вперед (t =1,12).
Таблица 1
|
|
Номер
наблюдения
|
Прибыль
|
%
по кредитованию юр. лиц
|
%
по депозитным вкладам
|
|
|
t
|
Yt
|
X1
|
X2
|
|
|
1
|
15
|
32
|
32
|
|
|
2
|
20
|
34
|
28
|
|
|
3
|
22
|
41
|
26
|
|
|
4
|
14
|
38
|
24
|
|
|
5
|
25
|
42
|
25
|
|
|
6
|
28
|
48
|
23
|
|
|
7
|
25
|
50
|
19
|
|
|
8
|
28
|
52
|
27
|
|
|
9
|
30
|
54
|
22
|
|
|
10
|
31
|
51
|
20
|
|
Сумма
|
55
|
238
|
442
|
246
|
|
Среднее
значение
|
5,5
|
23,8
|
44,2
|
24,6
|
Решение:
1. С помощью MS
Excel проведем корреляционный анализ:
Таблица 2
|
|
Yt
|
X1
|
X2
|
|
Yt
|
1
|
|
|
|
X1
|
0,889262
|
1
|
|
|
X2
|
-0,60731
|
-0,73681
|
1
|
Между показателями Прибыль и % по
кредитовании. Юр. Лиц существует очень тесная обратная связь, а между
показателями Прибыль и% по депозитным вкладам - тесная обратная связь, а между
показателями % по кредитованию юр. Лиц и % по депозитным вкладам - тесная
прямая.
2. Построить
линейную модель регрессии, описывающую зависимость y от факторов x1 и x2.
Таблица 3
|
Регрессионная
статистика
|
|
|
Множественный
R
|
0,892080282
|
|
R-квадрат
|
0,795807229
|
|
Нормированный
R-квадрат
|
0,737466437
|
|
Стандартная
ошибка
|
3,053335639
|
|
Наблюдения
|
10
|
Таблица 4
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
|
Регрессия
|
2
|
254,3399903
|
127,1699952
|
13,64067
|
|
Остаток
|
7
|
65,26000966
|
9,322858524
|
|
|
Итого
|
9
|
319,6
|
|
|
Таблица
5
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
-12,488
|
16,77412224
|
-0,744481454
|
|
X1
|
0,731
|
0,191250188
|
3,825912449
|
|
X2
|
0,16
|
0,38668388
|
0,41488867
|
Таблица 6
|
ВЫВОД
ОСТАТКА
|
|
|
|
Наблюдение
|
Предсказанное
Yt
|
Остатки
|
|
1
|
16,06036863
|
-1,0601
|
|
2
|
16,88205854
|
3,117
|
|
3
|
21,68314234
|
0,316
|
|
4
|
19,1671614
|
-5,167
|
|
5
|
22,25441806
|
2,745
|
|
6
|
26,32379539
|
1,676
|
|
7
|
27,1454853
|
-2,145
|
|
8
|
29,89234433
|
-1,892
|
|
9
|
30,55360348
|
-0,553
|
|
10
|
28,03762253
|
2,962
|
Уравнение регрессии зависимости объема зависимости
объема прибыли от ставки по кредитам
можно записать в следующем виде:
y=-12,488+0,731x1 +0,160x2.
3.
Оценить качество построенной модели. Вычислить для
модели среднюю ошибку аппроксимации и коэффициент детерминации.
В таблице 6 приведены вычисленные по модели значения
остаточные компоненты.
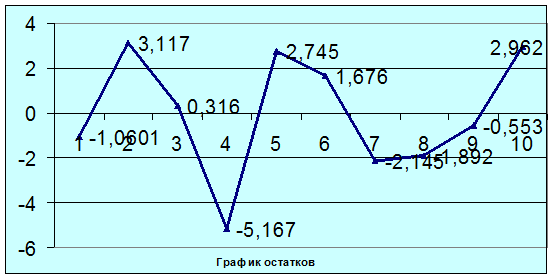
Вычислим для модели коэффициент детерминации.
Этот коэффициент уже вычислен нами и находится в
таблице 3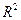 
=0.795.
Он показывает долю вариации результативного признака
под воздействием изучаемых факторов. Следовательно, около 80% вариации
зависимой переменной учтено в модели и обусловлено влиянием включенных
факторов.
Проверку значимости уравнения регрессии проведем на
основе вычисления F-критерия Фишера:
Fтабл мы вычисляем с помощью функции FРАСПОБР
Fтабл = 4,103
Fрасч уже вычислено и находится в таблице 4
Fрасч = 13,640
Поскольку .Ррасч
> Ртабл, уравнение
регрессии следует признать адекватным.
Учитывая, что
коэффициент регрессии невозможно использовать для непосредственной оценки
влияния факторов на зависимую переменную из-за различия единиц измерения, используем коэффициент
эластичности (Э) и бета-коэффициент, которые соответственно рассчитываются
по формулам:
Эj = аj*xср j /
yср
b = ai * Sxi /
Sy
|
|
у
|
х1
|
х2
|
|
|
х1
|
|
х2
|
|
|
|
Объем реализации
|
Ставка по
кредитам
|
Ставка по депозитам
|
уi-уср
|
(уi-уср)2
|
хi-хср
|
(хi-хср)2
|
хi-хср
|
(хi-хср)2
|
|
|
15
|
32
|
32
|
-8,8
|
77,44
|
-12,2
|
148,84
|
7,4
|
54,76
|
|
|
20
|
34
|
28
|
-3,8
|
14,44
|
-10,2
|
104,04
|
3,4
|
11,56
|
|
|
22
|
41
|
26
|
-1,8
|
3,24
|
-3,2
|
10,24
|
1,4
|
1,96
|
|
|
14
|
38
|
24
|
-9,8
|
96,04
|
-6,2
|
38,44
|
-0,6
|
0,36
|
|
|
25
|
42
|
25
|
1,2
|
1,44
|
-2,2
|
4,84
|
0,4
|
0,16
|
|
|
28
|
48
|
23
|
4,2
|
17,64
|
3,8
|
14,44
|
-1,6
|
2,56
|
|
|
25
|
50
|
19
|
1,2
|
1,44
|
5,8
|
33,64
|
-5,6
|
31,36
|
|
|
28
|
52
|
27
|
4,2
|
17,64
|
7,8
|
60,84
|
2,4
|
5,76
|
|
|
30
|
54
|
22
|
6,2
|
38,44
|
9,8
|
96,04
|
-2,6
|
6,76
|
|
|
31
|
51
|
20
|
7,2
|
51,84
|
6,8
|
46,24
|
-4,6
|
21,16
|
|
Сумма
|
238
|
442
|
246
|
-7,1054E-15
|
319,6
|
-2,842E-14
|
557,6
|
-1,421E-14
|
136,4
|
|
Сред.знач.
|
23,8
|
44,2
|
24,6
|
-7,1054E-16
|
31,96
|
-2,842E-15
|
55,76
|
-1,421E-15
|
13,64
|
Э1 = 0,731*44,2/23,8 =1,357
Э2 = 0,16*24,6/23,8 =0,156
b = 0,731* 304,7111 / 205,3778 = 1,138
b = 0,16* 123,7333 / 205,3778 = 0,010
|
S2y
|
205,3778
|
|
S2x1
|
304,7111
|
|
S2x2
|
123,7333
|
Коэффициент эластичности показывает, на сколько процентов изменяется
зависимая переменная при изменении фактора на один процент.
Бета-коэффициент с
математической точки зрения показывает, на какую часть величины среднего
квадратического отклонения меняется среднее значение зависимой переменной с изменением
независимой переменной на одно среднеквадратическое отклонение при фиксированном на
постоянном уровне значении остальных независимых переменных..