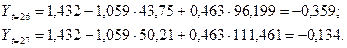Вариант 2
Задача состоит в построении модели для предсказания
цены квартиры в строящихся домах в Санкт-Петербурге в 1996 г.
Цена
квартиры – это зависимая переменная Y (тыс. долл.). В качестве независимых, объясняющих
переменных выбраны число комнат в квартире Х1 , общая площадь
квартиры Х3 (м2) , жилая площадь квартиры Х4
(м2) , площадь кухни Х5 (м2).
Требуется:
1. Осуществить выбор факторных признаков для построения
двухфакторной регрессионной модели.
2. Рассчитать параметры модели.
3. Для оценки качества всего уравнения регрессии
определить:
·
линейный
коэффициент множественной корреляции;
·
коэффициент
детерминации.
4. Осуществить оценку значимости уравнения регрессии.
5. Оценить с помощью t- критерия Стьюдента статистическую значимость
коэффициентов уравнения множественной регрессии.
6. Оценить влияние факторов на зависимую переменную по
модели.
7. Построить точечный и интервальный прогноз
результирующего показателя на два шага вперёд α = 0,1.
1. Построение
системы показателей (факторов).
Анализ
матрицы коэффициентов парной корреляции.
Выбор
факторных признаков для построения
Двухфакторной
регрессионной модели
Статистические данные по всем переменным приведены в
табл. 1. В этом примере n = 25, m = 4.
Таблица 1.
|
Y
|
X1
|
X3
|
X4
|
X5
|
|
Цена квартиры, тыс. долл.
|
Число
комнат
в квартире
|
Общая площадь
квартиры (м2)
|
Жилая
площадь
квартиры (м2)
|
Площадь
кухни (м2)
|
|
15,9
|
1
|
39,0
|
20,0
|
8,2
|
|
27,0
|
3
|
68,4
|
40,5
|
10,7
|
|
13,5
|
1
|
34,8
|
16,0
|
10,7
|
|
15,1
|
1
|
39,0
|
20,0
|
8,5
|
|
21,1
|
2
|
54,7
|
28,0
|
10,7
|
|
28,7
|
3
|
74,7
|
46,3
|
10,7
|
|
27,2
|
3
|
71,7
|
45,9
|
10,7
|
|
28,3
|
3
|
74,5
|
47,5
|
10,4
|
|
52,3
|
4
|
137,7
|
87,2
|
14,6
|
|
22,0
|
1
|
40,0
|
17,7
|
11,0
|
|
28,0
|
2
|
53,0
|
31,1
|
10,0
|
|
45,0
|
3
|
86,0
|
48,7
|
14,0
|
|
51,0
|
4
|
98,0
|
65,8
|
13,0
|
|
34,4
|
2
|
62,6
|
21,4
|
11,0
|
|
24,7
|
1
|
45,3
|
20,6
|
10,4
|
|
30,8
|
2
|
56,4
|
29,7
|
9,4
|
|
15,9
|
1
|
37,0
|
17,8
|
8,3
|
|
29,0
|
3
|
67,5
|
43,5
|
8,3
|
|
15,4
|
1
|
37,0
|
17,8
|
8,3
|
|
28,6
|
3
|
69,0
|
42,4
|
8,3
|
|
15,6
|
1
|
40,0
|
20,0
|
8,3
|
|
27,7
|
3
|
69,1
|
41,3
|
8,3
|
|
34,1
|
2
|
68,1
|
35,4
|
13,0
|
|
37,7
|
2
|
75,3
|
41,4
|
12,1
|
|
41,9
|
3
|
83,7
|
48,5
|
12,1
|
Использование
инструмента Корреляция
(Анализ данных в EXCEL)
Для проведения корреляционного анализа выполним
следующие действия:
1. Данные для корреляционного анализа выполним следующие
действия:
2. Выберем команду Сервис→Анализ данных.
3. В диалоговом окне Анализ данных выберем инструмент Корреляция, а затем щелкните на кнопке
ОК.
4. В диалоговом окне Корреляция
в поле Входной интервал
необходимо ввести диапазон ячеек, содержащих исходные данные. Так как выделены и заголовки столбцов, то установим
флажок Метки в первой строке.
5. Выберем параметры вывода. В данном примере Новый рабочий лист.
6. ОК.
Результат корреляционного анализа
Таблица
2.
|
|
Цена квартиры,
тыс. долл.
|
Число
комнат
в квартире
|
Общая площадь
квартиры (м2)
|
Жилая
площадь
квартиры (м2)
|
Площадь
кухни (м2)
|
|
Цена квартиры,
тыс. долл.
|
1
|
|
|
|
|
|
Число
комнат
в квартире
|
0,800871004
|
1
|
|
|
|
|
Общая площадь
квартиры (м2)
|
0,9121706
|
0,8984863
|
1
|
|
|
|
Жилая
площадь
квартиры (м2)
|
0,849511981
|
0,9261784
|
0,9746318
|
1
|
|
|
Площадь
кухни (м2)
|
0,793012327
|
0,4986779
|
0,7166486
|
0,6241815
|
1
|
Анализ матрицы коэффициентов парной корреляции
показывает, что зависимая переменная, т.е. цена квартиры, имеет тесную связь с числом
комнат (ryx1 = 0,801), с общей площадью квартиры (ryx3 = 0,912), с жилой
площадью квартиры (ryx4 = 0,850)
и с площадью кухни (ryx5 = 0,793).
Однако факторы Х3 и Х4 тесно связаны между собой (rx3 x4 =
0,975), что свидетельствует о наличии мультиколлинеарности. Из этих двух
переменных оставим в модели Х3 – общая площадь квартиры. В этом
примере n = 25,
m
= 4, после исключения незначимых факторов n = 25, k = 2.
2. Выбор вида
модели и оценка ее параметров
Таблица 3.
|
Y
|
X1
|
X2
|
|
Цена
квартиры,
тыс. долл.
|
Число комнат
|
Общая
площадь
квартиры
(м2)
|
|
15,9
|
1
|
39,0
|
|
27,0
|
3
|
68,4
|
|
13,5
|
1
|
34,8
|
|
15,1
|
1
|
39,0
|
|
21,1
|
2
|
54,7
|
|
28,7
|
3
|
74,7
|
|
27,2
|
3
|
71,7
|
|
28,3
|
3
|
74,5
|
|
52,3
|
4
|
137,7
|
|
22,0
|
1
|
40,0
|
|
28,0
|
2
|
53,0
|
|
45,0
|
3
|
86,0
|
|
51,0
|
4
|
98,0
|
|
34,4
|
2
|
62,6
|
|
24,7
|
1
|
45,3
|
|
30,8
|
2
|
56,4
|
|
15,9
|
1
|
37,0
|
|
29,0
|
3
|
67,5
|
|
15,4
|
1
|
37,0
|
|
28,6
|
3
|
69,0
|
|
15,6
|
1
|
40,0
|
|
27,7
|
3
|
69,1
|
|
34,1
|
2
|
68,1
|
|
37,7
|
2
|
75,3
|
|
41,9
|
3
|
83,7
|
Применение инструмента Регрессия
(Анализ данных в EXCEL)
Для
проведения регрессионного анализа выполним следующие действия:
1. Выберем команду Сервис→Анализ данных.
2. В диалоговом окне Анализ данных выберем инструмент Регрессия, а затем щелкнем на кнопку ОК.
3. В диалоговом окне Регрессия
в поле Входной интервал Y
введем адрес одного диапазона ячеек,
который представляет зависимую переменную. В поле Входной интервал Х введем адреса одного или нескольких диапазонов,
которые содержат значения независимых переменных (рис. 1.1).
4. Так как выделены и заголовки столбцов, то установим
флажок Метки в первой строке.
5.
Выберем
параметры ввода. В данном примере Новая
рабочая книга.
6. В поле Остатки
поставим необходимые флажки.
7. ОК.
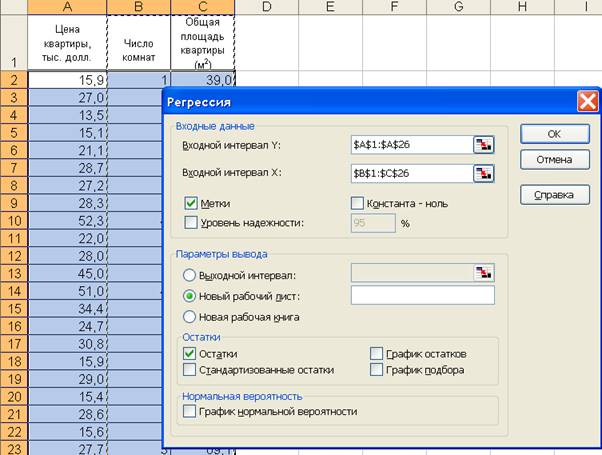
Рис. 1. 1. Диалоговое окно Регрессия
подготовлено к выполнению анализа данных
Результат регрессионного анализа содержится в табл. 4
– 7.
Рассмотрим
содержание этих таблиц.
Таблица 4.
|
Регрессионная статистика
|
|
|
Множественный R
|
0,913
|
|
R-квадрат
|
0,834
|
|
Нормированный R-квадрат
|
0,819
|
|
Стандартная ошибка
|
4,645
|
|
Наблюдения
|
25
|
Таблица
5.
|
Дисперсионный анализ
|
df
|
SS
|
MS
|
F
|
|
Регрессия
|
2
|
2382,548
|
1191,274
|
55,213
|
|
Остаток
|
22
|
474,670
|
21,576
|
|
|
Итого
|
24
|
2857,218
|
|
|
Таблица
6.
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
|
Y-пересечение
|
1,432
|
2,755
|
0,520
|
|
Число
комнат
|
-1,059
|
2,160
|
-0,490
|
|
Общая
площадь
квартиры
(м2)
|
0,463
|
0,092
|
5,049
|
Таблица 7.
Вывод
остатка
|
Наблюдение
|
Предсказанное
|
Остатки
|
|
|
|
|
|
1
|
18,45
|
-2,55
|
|
2
|
29,95
|
-2,95
|
|
3
|
16,50
|
-3,00
|
|
4
|
18,45
|
-3,35
|
|
5
|
24,66
|
-3,56
|
|
6
|
32,87
|
-4,17
|
|
7
|
31,48
|
-4,28
|
|
8
|
32,78
|
-4,48
|
|
9
|
61,01
|
-8,71
|
|
10
|
18,91
|
3,09
|
|
11
|
23,87
|
4,13
|
|
12
|
38,11
|
6,89
|
|
13
|
42,61
|
8,39
|
|
14
|
28,32
|
6,08
|
|
15
|
21,37
|
3,33
|
|
16
|
25,45
|
5,35
|
|
17
|
17,52
|
-1,62
|
|
18
|
29,54
|
-0,54
|
|
19
|
17,52
|
-2,12
|
|
20
|
30,23
|
-1,63
|
|
21
|
18,91
|
-3,31
|
|
22
|
30,28
|
-2,58
|
|
23
|
30,87
|
3,23
|
|
24
|
34,21
|
3,49
|
|
25
|
37,04
|
4,86
|
График остатков изображен на рис. 1.2.
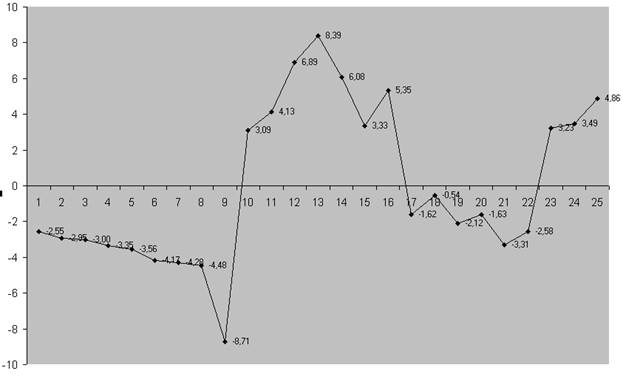
Рис. 1.2. График остатков
3.
Оценка качества всего уравнения регрессии
В таблице 7 приведены вычисленные (предсказанные) по
модели зависимой переменной Y и значения остаточной компоненты εi .
Значение коэффициентов детерминации и множественной
корреляции можно найти в таблице Регрессионная статистика.
Коэффициент детерминации:
R2 = R2yx1x2 = 1 -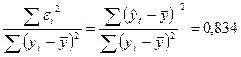 
Он показывает долю вариации результативного признака
под воздействием изучаемых факторов. Следовательно, около 83,4% вариации
зависимой переменной учтено в модели и обусловлено влиянием включенных
факторов.
Коэффициент множественной корреляции R:
R =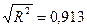 
Он показывает тесноту связи зависимой переменной Y с
двумя включенными в модель объясняющими факторами. Следовательно связь весьма
тесная.
4. Проверку значимости уравнения регрессии произведем
на основе вычисления F-критерия
Фишера:
F=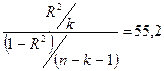
4.
Проверку значимости уравнения регрессии произведем на
основе F-критерия
Фишера
Значение F-критерия
Фишера можно найти в табл. 5 протокола EXСEL.
Табличное значение F-критерия можно найти с помощью функции FРАСПОБР (рис. 1.3).
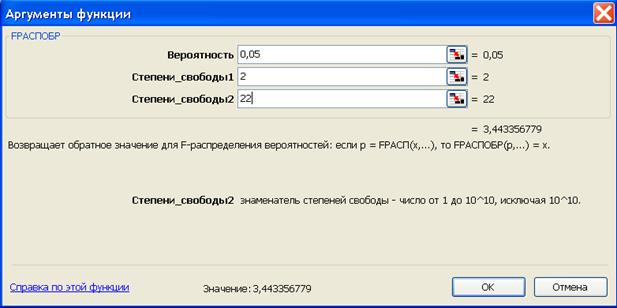
Рис. 1.3. Определение табличного значения F-критерия
Табличное значение F-критерия при доверительной вероятности 0,95 при
ν1 = k = 2 и ν2 = n – k = 25 – 2 –
1 = 22 составляет 3,44.
Поскольку Fрас
> Fтабл, уравнение регрессии следует признать адекватным.
5.
Оценить с помощью t-критерия Стьюдента статистическую значимость
коэффициентов уравнения множественной регрессии
Значимость коэффициентов уравнения регрессии а0, а1, а2 оценим
с использованием t-критерия Стьюдента.
Расчетные значения t-критерия Стьюдента для коэффициентов уравнения
регрессии а1, а2 приведены в четвертом
столбце табл. 6 протокола EXCEL. Табличное
значение t-критерия Стьюдента
можно найти с помощью функции СТЬЮДРАСПОБР (рис. 1.4).
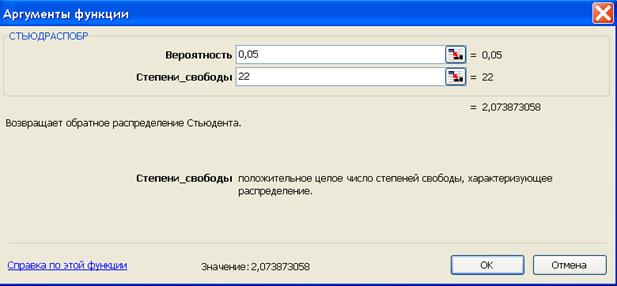
Рис. 1.4. Определение табличного
значения t-критерия Стьюдента
Табличное значение t-критерия при 5%-ном уровне значимости и степенях
свободы (25 – 2 – 1) составляет 2,07. Так как для а1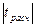 
<
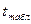, а для а2 
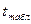> , то следовательно коэффициент а1 статистически незначим, а коэффициент а2 статистически значим.
6.
Проанализировать влияние факторов на зависимую переменную по модели (для
каждого коэффициента регрессии вычислить коэффициент эластичности,
β-коэффициент)
Учитывая, что коэффициент регрессии невозможно использовать
для непосредственной оценки влияния факторов на зависимую переменную из-за
различия единиц измерения, используем коэффициент
эластичности (Э) и бета-коэффициент,
которые соответственно рассчитываются по формулам:
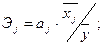
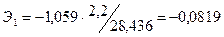
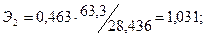
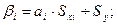
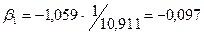
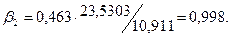
Коэффициент эластичности показывает, на сколько
процентов изменяется зависимая переменная при изменении фактора на один
процент.
Бета-коэффициент с математической точки зрения
показывает, на какую часть величины среднего квадратического отклонения
меняется среднее значение зависимой переменной с изменением независимой
переменной на одно среднеквадратическое отклонение при фиксированном на
постоянном уровне значении остальных независимых переменных. Это означает, что
при уменьшении числа комнат на единицу цена квартиры уменьшится на 1 тыс. долл.
(- 0,097 ·10,911).
7.
Определить точечные прогнозные оценки цены квартиры на два квартала вперед (t0,7 =1,12)
Исходные данные представлены временными рядами,
поэтому прогнозные значения Х1,26, Х2,26 и Х1,27,
Х2,27 можно определить с помощью экспертных оценок, с помощью
средних абсолютных приростов или вычислить на основе экстраполяционных методов.
Для фактора Х1 Число комнат в квартире выбрана
модель
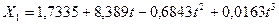, по которой
получен прогноз на 2 месяца вперед. График модели временного ряда Число
комнат в квартире приведен на рис. 1.5.
|
Упреждение
|
Прогноз
|
|
1
|
43,75
|
|
2
|
50,21
|
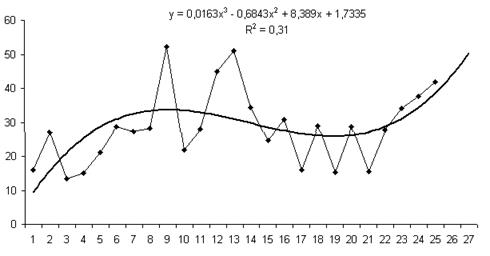
Рис 1.5. Прогноз показателя Число
комнат в квартире
Для временного ряда Общая площадь квартиры в
качестве аппроксимирующей функции в аппроксимирующей функции выбран полином
третьей степени (парабола), по которой построен прогноз на 2 шага вперед. На
рис. 1.6 приведен результат построения тренда для временного ряда Общая
площадь квартиры.
.
|
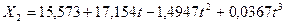Упреждение
|
Прогноз
|
|
1
|
96,199
|
|
2
|
111,461
|
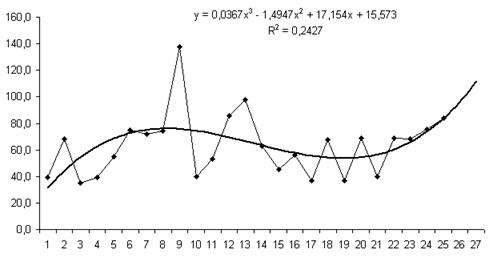
Рис. 1.6.
Прогноз показателя Общая площадь квартиры
Для получения прогнозных оценок зависимостей
переменной по модели
подставим
в нее найденные прогнозные значения факторов Х1 и Х2:
