Цель работы.
Освоить
методику построения модели множественной регрессии с использованием пакета
программ Statgraphics Plus.
Порядок
выполнения работы
Таблица с исходными данными:
Y Х1 X2 X3
178263 47,8 217 -1,2
31662 45,1 220 -25,4
24589 39,8 219 -28,5
87404 37,1 217 -21,3
576864 37,4 220 10,7
627909 35,5 229 2,9
Проверка мультиколлениарности исходных данных
и отбор определяющих факторов для построения модели:
Матрица
коэффициентов парной корреляции. Матрица является продолжением таблицы с
исходными данными
|
y
|
X1
|
X2
|
X3
|
|
y
|
1
|
-0,54852
|
0,703626
|
0,891564
|
|
X1
|
-0,54852
|
1
|
-0,50968
|
-0,20572
|
|
X2
|
0,703626
|
-0,50968
|
1
|
0,386584
|
|
X3
|
0,891564
|
-0,20572
|
0,386584
|
1
|
Матрица
мультиколлинеарна, так как на пересечениях столбцов Х нет значений превышающих
0,8 по модулю
Отбираем для множественного
регрессионного анализа определяющие переменные и записываем имена колонок с их
расположением Col_1, Col_3 и т.д. Col_2 не отбираем, т.к. эта графа является просто нумерацией строк.
Нахождение точечных оценок уравнения регрессии,
анализ адекватности модели и значимости коэффициентов уравнения
Выполняем
множественный регрессионный анализ с отобранными данными, для чего в главном
меню вызваем программу Multiple regression. В окно Dependent Variable заносим имя
колонки с результирующей переменной (Col_1).
В окно Independent Variables заносим имена
колонок с отобранными факторными переменными.
При
этом на экране появятся результаты выполненного регрессионного анализа в
табличной форме и в виде текста.
|
Standard T
|
|
|
|
|
Parameter Estimate Error Statistic P-Value
|
|
|
-----------------------------------------------------------------------------
|
|
|
|
|
CONSTANT
-3,09771E6 1,16179E6 -2,66633 0,1166
|
|
|
Col_2 -13885,9 4140,09 -3,354 0,0786
|
|
|
Col_3 18335,5 4850,49 3,78015 0,0634
|
|
|
Col_4 12047,1 1144,88 10,5227 0,0089
|
|
|
-----------------------------------------------------------------------------
|
|
|
|
|
|
|
|
|
|
|
|
|
Analysis of
Variance
|
|
|
|
|
|
-----------------------------------------------------------------------------
|
|
|
|
|
Source
Sum of Squares Df Mean Square F-Ratio P-Value
|
|
|
-----------------------------------------------------------------------------
|
|
|
|
|
Model 3,76529E11 3
1,2551E11 81,70
0,0121
|
|
|
Residual 3,07246E9 2
1,53623E9
|
|
|
|
|
-----------------------------------------------------------------------------
|
|
|
|
|
Total (Corr.) 3,79602E11 5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared = 99,1906 percent
|
|
|
|
|
|
|
R-squared (adjusted for d.f.) = 97,9765 percent
|
|
|
|
|
Standard Error of Est. = 39194,8
|
|
|
|
|
|
Mean absolute error = 20596,1
|
|
|
|
|
|
|
Durbin-Watson statistic = 2,91608
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Col_1 = -3,09771E6 - 13885,9*Col_2 + 18335,5*Col_3 +
12047,1*Col_4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Unusual Residuals
|
|
|
|
|
|
--------------------------------------------------------------
|
|
|
|
|
|
Predicted Studentized
|
|
|
|
|
Row
Y Y Residual Residual
|
|
|
|
|
--------------------------------------------------------------
|
|
|
|
|
|
1
178263,0 202906,0 -24642,6 -3,58
|
|
|
|
5
576864,0 545686,0 31177,7 9,10
|
|
|
|
6
627909,0 643122,0 -15212,8 -8,16
|
|
|
|
--------------------------------------------------------------
|
|
|
|
|
В
первой таблице приводятся рассчитанные по методу м.н.к. коэффициенты уравнения
регрессии с выбранными факторными переменными. В в .еменныхми факторными ости коэффициентов уравнениям виде
Вграфе
Parameter приводятся имена факторных переменных Constant, Col_3, Col_4 и т.д. Во второй графе Estimate указываются точечные оценки параметров модели, в графе Standard Error приводятся стандартные ошибки параметров, а в графе T Statistic приводятся расчетные значения t- критерия Стьюдента для рассчитанных
параметров.
Во
второй таблице Analysis of Variance приводятся
результаты дисперсионного анализа. В первой строке таблицы Model приводится дисперсия регрессии, во второй Residual – дисперсия остатка. Графы слева на право означают: сумму квадратов – Sum of Squares, число степеней свободы – Df, оценку дисперсии – Mean Square, расчетный критерий Фишероа – F-Ratio.
Ниже
таблицы приводятся:
Коэффициент
детерминации R-squared в процентах;
Нормированный
коэффициент R-квадрат
R-squared(adjusted for d.f.);
Стандартная ошибка Standard Error of Est.;
Среднее
значение абсолютной ошибки Mean absolute error;
Статистика
Дурбина – Ватсона.
|
Col_1 = -3,09771E6 - 13885,9*Col_2 + 18335,5*Col_3 + 12047,1*Col_4
|
- запись
линейного уравнения регрессии.
Нажимаем Tabular option нажимаем проверку (предпоследняя
строчка)-выводятся данные ошибок, выбираем наибольшее значение по модулю
(ошибку) и удаляем данную строку в своём варианте, затем снова запускаем
программу (предварительно убираем проверку ошибок)
|
Standard T
|
|
|
|
Parameter Estimate Error Statistic P-Value
|
|
-----------------------------------------------------------------------------
|
|
|
|
CONSTANT
-4,33851E6 225505,0 -19,239 0,0331
|
|
Col_2 -10439,8 743,637 -14,0388 0,0453
|
|
Col_3 23175,8 919,35 25,2089 0,0252
|
|
Col_4 10259,4 264,467 38,7929 0,0164
|
|
-----------------------------------------------------------------------------
|
|
|
|
|
|
|
|
|
|
|
Analysis of
Variance
|
|
|
|
|
-----------------------------------------------------------------------------
|
|
|
|
Source
Sum of Squares Df Mean Square F-Ratio P-Value
|
|
-----------------------------------------------------------------------------
|
|
|
|
Model 2,54823E11 3
8,4941E10 2314,68 0,0151
|
|
Residual 3,66967E7 1
3,66967E7
|
|
|
|
-----------------------------------------------------------------------------
|
|
|
|
Total (Corr.) 2,5486E11 4
|
|
|
|
|
|
|
|
|
|
|
|
R-squared = 99,9856 percent
|
|
|
|
|
|
R-squared (adjusted for d.f.) = 99,9424 percent
|
|
|
|
Standard Error of Est. = 6057,78
|
|
|
|
|
Mean absolute error = 2218,93
|
|
|
|
|
|
Durbin-Watson statistic = 3,49002
|
|
|
|
|
|
|
|
|
|
|
|
Col_1 = -4,33851E6 - 10439,8*Col_2 + 23175,8*Col_3 +
10259,4*Col_4
|
Значение Ф-критерия Фишера при уровне значимости а=0,05 равно
215,72 (1 строка, 3 столбец),
полученный нами результат равен 2314,68, отсюда следует что наша модель
адекватна
В связи с тем, что на данном компьютерере программа не поддерживает
построение графиков п. 3.11 выполнен в п.п. 3.7-3.8
Расчет
коэффициента эластичности и коэффициента «бета»
Для
получения статистических оценок по исходным данным и результатам вычислений
вызваем из главного меню Statgraphics
Plus программу Multiple-Variable Analysis. В окно Data вызваем идентификаторы анализируемых данных (Col_3,Col_6)
из таблицы исходных данных, т.е. факторов, вошедших в модель и результатного
признака.. В командах Tabular options помечаем окно Summary Statistics\ OK. Из таблицы выписываем среднее значение Average, отклонение Variance, стандартное отклонение Standard deviation. Средние значения, стандартные отклонения
будем использовать для расчета коэффициентов эластичности, бета коэффициентов регрессионной модели.
По
формулам:
|
|
|
|
|
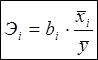 |
|
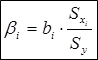 |
|
Col_1 Col_2 Col_3
|
|
|
--------------------------------------------------------------------------------
|
|
|
Count 5 5 5
|
|
|
Average 189965,0 41,06 220,4
|
|
Variance
6,37149E10 27,483 24,8
|
|
Standard deviation
252418,0 5,24242 4,97996
|
|
Minimum
24589,0 35,5 217,0
|
|
Maximum
627909,0 47,8 229,0
|
|
Stnd. skewness
1,76017
0,359414 1,70817
|
|
Stnd. kurtosis
1,72733
-0,981888 1,67438
|
|
Sum
949827,0 205,3 1102,0
|
|
--------------------------------------------------------------------------------
|
|
|
|
|
|
|
|
|
|
Col_4
|
|
|
|
|
|
--------------------------------------------------------------------------------
|
|
|
Count
5
|
|
|
|
|
|
Average
-14,7
|
|
|
|
|
|
Variance
210,125
|
|
|
|
|
Standard deviation
14,4957
|
|
|
|
|
Minimum
-28,5
|
|
|
|
|
Maximum
2,9
|
|
|
|
|
Stnd. skewness
0,470978
|
|
|
|
|
Stnd. kurtosis
-1,31983
|
|
|
|
|
Sum
-73,5
|
|
|
|
|
|
--------------------------------------------------------------------------------
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Average
(среднее значение)
|
|
|
|
|
|
Variance
(отклонение)
|
|
|
|
|
|
Standard
deviation (стандартное отклонение)
|
|
|
|
|
|
|
|
|
|
|
Эластичность
= А * (средний х / средний у)
|
|
|
|
|
|
|
|
|
|
|
Бетта
коэфициент = А * (стандартное отклонение х/стандартное отклонение у)
|
|
|
|
|
|
|
|
|
Эластичность
|
|
|
|
|
|
Col_2
= 10439,8*(41,06/189965)
|
|
2,256511
|
|
|
|
Col_3
= 23175,8*(220,4/189965)
|
|
26,88888
|
|
|
|
Col_4
= 10259,4*(-14,7/189965)
|
|
-0,7939
|
|
|
|
|
|
|
|
|
|
|
Бетта
коэффициент
|
|
|
|
|
|
Col_2 =10439,8*(5,24242/252418)
|
0,216822
|
|
|
|
Col_3 =23175,8*(4,97996/252418)
|
0,457236
|
|
|
|
Col_4 =10259,4*(14,4957/252418)
|
0,58917
|
|
|
Вывод:
Мы
освоили методику построения модели множественной регрессии с использованием
пакета программ Statgraphics Plus. Мы построили модель множественной регрессии,
улучшили ее, определили ее адекватность , нашли коэффициенты эластичности и
бета-коэффициенты