Небольшая фирма производит два вида продукции: столы и стулья. Для изготовления одного стула требуется 3 м древесины, а для изготовления одного стола – 7 м. На изготовление одного стула уходит 2 ч рабочего времени, а на изготовление стола – 8 ч. Каждый стул приносит 1 ден. ед. прибыли, а каждый стол – 3 ден. ед. Сколько стульев и сколько столов должна изготовить эта фирма, если она располагает 20 м древесины и 400 ч рабочего времени, чтобы получить максимальную прибыль?

Решение. Приведем подробное описание технологии получения решения приведенной ЗЛП.

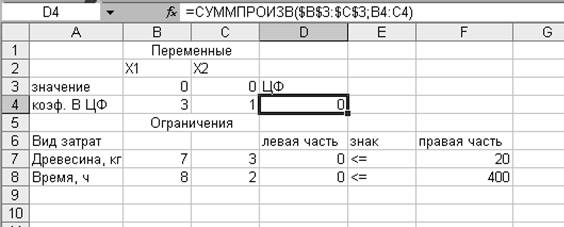
1. Создаем форму для ввода условий задачи. Запускаем Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows.Открывается чистый лист Excel. Создаем текстовую форму – таблицу для ввода условий задачи.

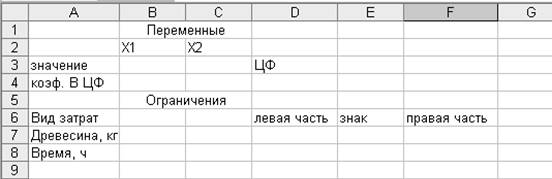
2. Указываем адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначим через Х1 – количество столов, Х2 – количество стульев. В нашей задаче оптимальные значения компонент вектора Х=(Х1, Х2) будут помещены в ячейках В3:С3, оптимальное значение целевой функции – в ячейке D4.

3. Вводим исходные данные задачи в созданную форму-таблицу.

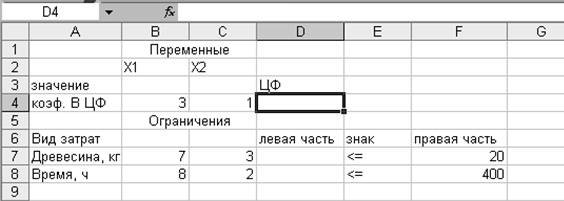
4. Вводим зависимость для целевой функции:

• Курсор в ячейку D4.

• Щелкнем на кнопку «Мастер функций», расположенную на панели инструментов.

• На экране появляется диалоговое окно Мастер функций - шаг 1 из 2.

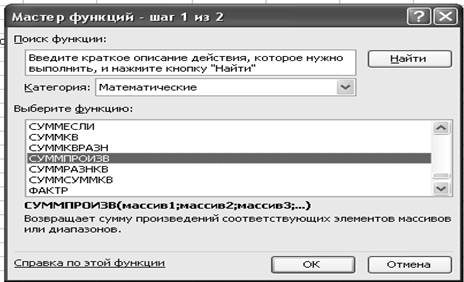
• В окне «Категория» выбираем категорию Математические. В окне Функции выбираем СУММПРОИЗВ.

• На экране появляется окно СУММПРОИЗВ.

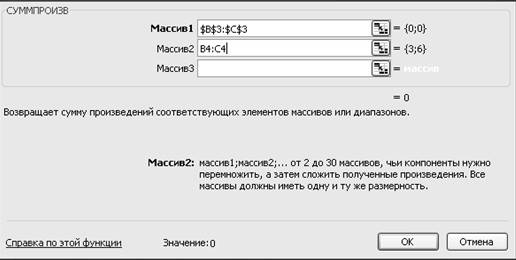
• В строку «Массив 1» вводим $В$3:$С$3. В строку «массив 2» вводим В4:С4 → ОК.

 5. Вводим зависимости для ограничений:

• Курсор в ячейку D4. На панели инструментов нажимаем кнопку Копировать в буфер.

• Курсор в ячейку D7 → Вставить из буфера.

• Курсор в ячейку D8 → Вставить из буфера.

Проверяем содержимое ячеек D7:D8.

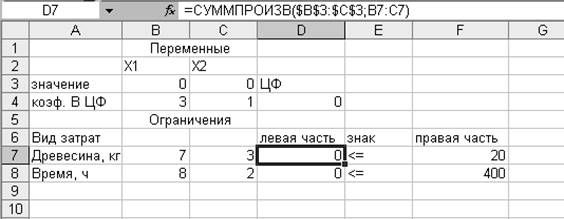
В строке Меню нажимаем Сервис → Поиск решения. Появляется диалоговое окно Поиск решения.

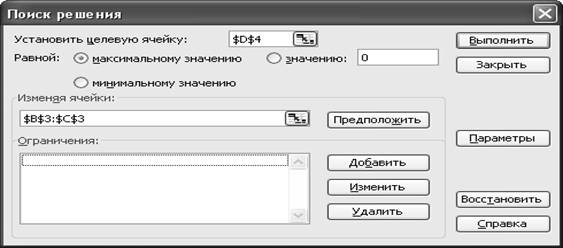
6. Назначаем целевую функцию:

• ставим курсор в строку Установить целевую функцию, вводим адрес ячейки $D$4;

• вводим направление целевой функции – Максимальному значению;

• ставим курсор в строку Изменяя ячейки, вводим адреса искомых переменных $B$3:$C$3.

7. Вводим ограничения:

• щелкнем на кнопку Добавить. Появляется диалоговое окно Добавление ограничения.

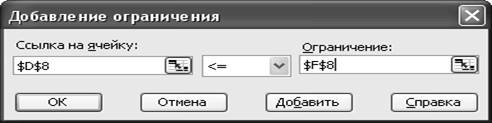
• в строке Ссылка на ячейку вводим адрес $D$8;

• вводим знак ограничения <= ;

• в строке ограничения вводим адрес $F$8;

• щелкаем на кнопку Добавить, на экране вновь диалоговое окно Добавление ограничения;

• вводим остальные ограничения задачи → ОК.

На экране появляется диалоговое окно Поиск решения с введенными условиями.

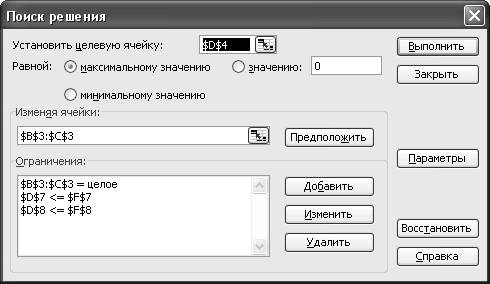
8. Вводим параметры для решения ЗЛП:

• в диалоговом окне щелкаем на кнопку Параметры. На экране появляется диалоговое окно Параметры поиска решения;

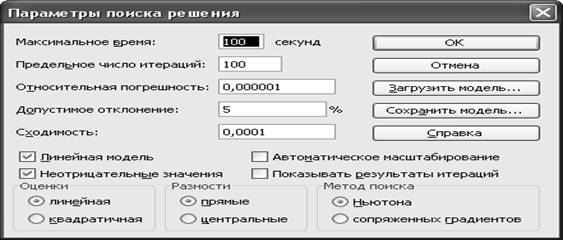
• устанавливаем флажки в окнах Линейная модель и Неотрицательные значения → ОК. На экране диалоговое окно Поиск решения, щелкаем на кнопке Выполнить.

Через непродолжительное время появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками В3:С3 для значений Х1 и Х2 и ячейка D4 с максимальным значением целевой функции.

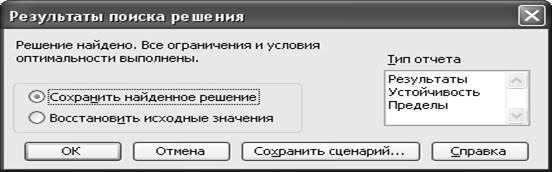
Полученное решение означает, что максимальный доход 8 ден. ед. фирма может получить при выпуске и реализации 2 столов и 2 стульев. При этом древесина будет использована полностью, а из 400 часов рабочего времени будет использовано 20.

Задача 3.

Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

Решение. Обозначим за Х₁ количество обычных наборов удобрений, за Х₂ – улучшенных.

f(X)=3X₁+4X₂→min

3X₁+2X₂≥10

4X₁+6X₂≥20

X₁+3X₂≥7

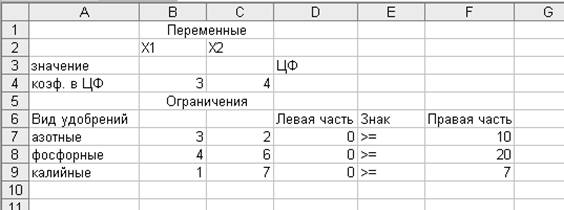
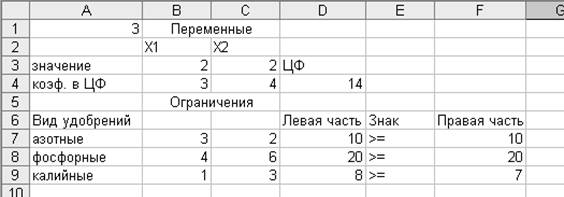
Полученное решение означает, что минимальную стоимость 14 ден. ед. можно получить при покупке 2 кг обычного набора удобрений и 2 кг улучшенного. При этом азотных и фосфорных удобрений потребуется 10 и 20 кг соответственно, а калийных на 1 кг больше (8 кг).

Задача 4.

На имеющихся у фермера 400 га земли он планирует посеять кукурузу и сою. Сев и уборка кукурузы требуют на каждый гектар 200 ден. ед. затрат, а сои – 100 ден. ед. На покрытие расходов, связанных с севом и уборкой, фермер получил ссуду в 60 тыс. ден. ед. Каждый гектар, засеянный кукурузой, принесет 30 ц, а каждый гектар, засеянный соей, - 60 центнеров. Фермер заключил договор на продажу, по которому каждый центнер кукурузы принесет ему 3 ден. ед., а каждый центнер сои – 6 ден. ед. прибыли. Однако согласно этому договору фермер обязан хранить убранное зерно в течении нескольких месяцев на складе, максимальная вместимость которого равна 21 тыс. ц. Сколько гектар нужно засеять каждой из этих культур, чтобы получить максимальную прибыль?

Решение. Х₁ – количество гектар кукурузы, Х₂ – сои.

F(X)=30*3*X₁+60*6*X₂→max

200X₁+100X₂≤60000

30X₁+60X₂≤21000

X₁+X₂≤400

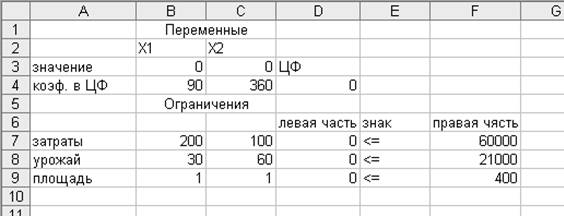
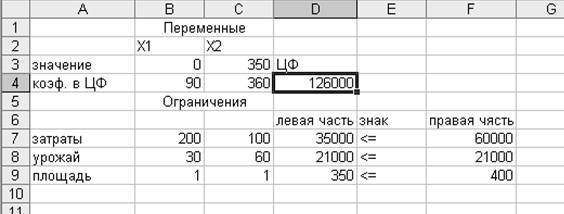
Полученное решение означает, что для получения максимальной прибыли 126000 ден. ед. нужно засеять кукурузой 0 га, а соей 350 га. При этом количество урожая должно быть равно вместимости склада, затраты будут составлять из 60000 – 35000, а из 400 га земли будет использовано 350 га.

Задача 7.

Фирма выпускает три вида кожаных изделий. На изготовление единицы продукции первого вида затрачивается 0,2 ч работы дубильного участка, 0,6 ч работы раскройного участка и 0 ч работы завершающего участка; на изготовление второго изделия – 0,3; 0,5; 0 ч; на изготовление третьего изделия – 0,4; 0,4; 0 ч соответственно. Прибыль от единицы продукции первого вида – 6 ден. ед., второго вида – 7 ден. ед., третьего вида – 10 ден. ед. В течение месяца рабочее время каждого участка ограничено следующим образом:

дубильного участка – 320 ч;

раскройного участка – 400 ч;

завершающего участка – 160 ч.

Сколько изделий каждого вида должна выпустить фирма за месяц, чтобы прибыль была максимальной?

Решение. Х₁ – количество изделий 1-го вида, Х₂ – 2-го вида.

F(X)=6X₁+7X₂+10X₃→max

0,2X₁+0,3X₂+0,4X₃≤320

0,6X₁+0,5X₂+0,4X₃≤400

0X₁+0X₂+0,8X₃≤160

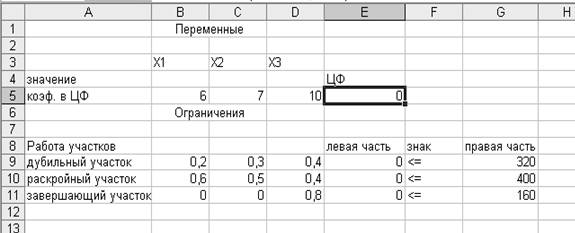
Полученное решение означает, что максимальная прибыль 6480 ден. ед. может быть достигнута при выпуске 0 изделий первого вида, 640 изделий второго вида и 200 изделий третьего вида. При этом раскройный и завершающий участки работают максимальное количество часов, а работа дубильного участка сокращена до 272 часов.

Задача 9.

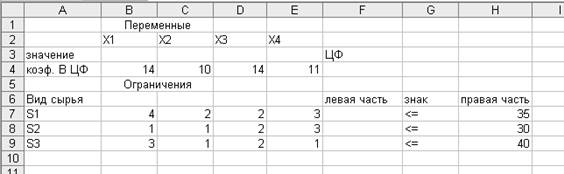
Для составления плана выпуска четырех видов продукции Р₁, Р₂, Р₃ и Р₄ на предприятии используют три вида сырья S₁, S₂ и S₃. Объемы выделенного сырья, нормы расхода сырья и прибыль, полученная в результате выпуска каждого вида продукции, приведены в таблице. Какое количество продукции всех видов необходимо производить, чтобы прибыль была максимальной?

Решение. Х₁, Х₂, Х₃, Х₄ – количество продукции Р₁, Р₂, Р₃, Р₄ соответственно.

F(X)=14X₁+10X₂+14X₃+11X₄→max

4X₁+2X₂+2X₃+3X₄≤35

X₁+X₂+2X₃+3X₄≤30

3X₁+X₂+2X₃+X₄≤40

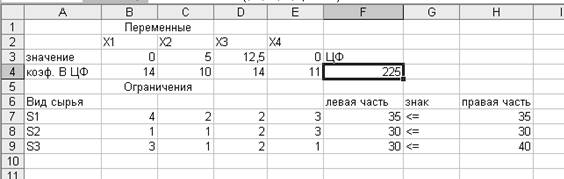
Полученное решение означает, что максимальную прибыль 225 ден. ед. предприятие может получить при производстве Р₁=0, Р₂=5, Р₃=12,5, Р₄=0 изделий. При этом запасы сырья S₁ и S₂ израсходуются полностью, а сырье S₃ – на 10 меньше (30).

Задача 10

Намечается выпуск двух видов костюмов – мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм – 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-день трудозатрат. Определите число костюмов каждого вида, обеспечивающее максимальную прибыль предприятию. Прибыль от реализации женского костюма составляет 10 ден. ед., а от мужского – 20 ден. ед. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов и обеспечить прибыль не менее 1400 ден.ед.

Решение. Х₁ – количество мужских костюмов, Х₂ – количество женских костюмов.

f(X)=20X₁+10X₂→max

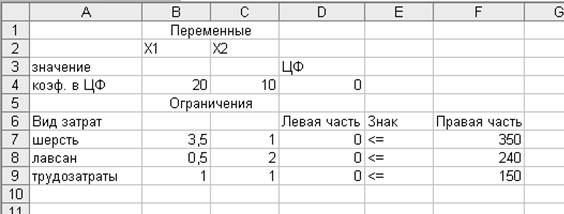
3,5X₁+X₂≤350

0,5X₁+2X₂≤240

X₁+X₂≤150

X₂≥60

20X₁+10X₂≥1400

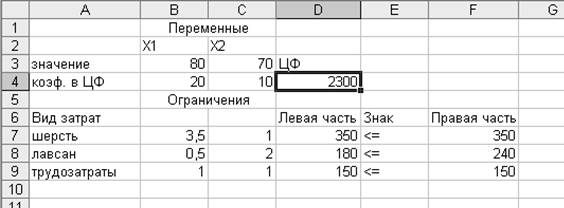
Полученное решение означает, что максимальная прибыль предприятия – 2300 ден.ед. будет достигнута при выпуске 80 мужских и 70 женских костюмов. При этом шерсть и трудозатраты будут использованы полностью, а из 240 м лавсана будет использовано 180.

Задача 17

Пусть предприятие (например, мебельная фабрика) производит столы и стулья. Расход ресурсов на их производство и прибыль от их реализации представлены в таблице.

Кроме того, на производство 80 столов заключен контракт с муниципалитетом, который, безусловно, должен быть выполнен. Составьте такую оптимальную производственную программу, чтобы прибыль от реализации продукта была максимальной.

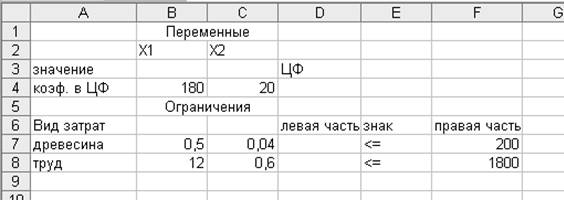
Решение. Х₁ – количество столов, Х₂ – количество стульев.

F(X)=180X₁+20X₂→max

0,5X₁+0,04X₂≤200

12X₁+0,6X₂≤1800

X₁≥80

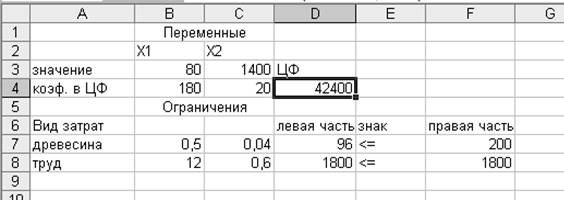
Полученное решение означает, что максимальная прибыль предприятия 42400 ден. ед. будет достигнута при производстве 80 столов и 1400 стульев. При этом трудовые ресурсы будут задействованы полностью, а расход древесины будет составлять из 200 м³ – 96 м³.

Задача 19

При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса даны в таблице.

Прибыль от реализации одной единицы товара первого вида составляет 2 ден. ед., второго вида – 3 ден. ед.

Составьте оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль.

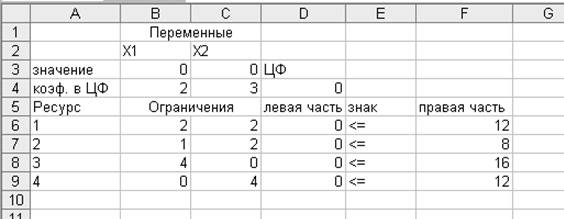
Решение. Х₁ – количество товаров 1-го вида, Х₂ – 2-го вида.

F(X)=2X₁+3X₂→max

2X₁+2X₂ ≤12

X₁+2X₂ ­≤8

4X₁+0X₂ ≤16

0X₁+4X₂ ≤12

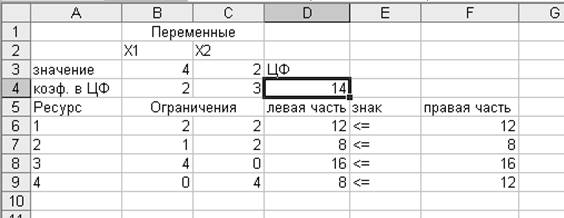
Полученное решение означает, что максимальная прибыль 14 ден. ед. будет достигнута при продаже 4-х товаров 1-го вида и 2-х товаров 2-го вида. При этом 1, 2, 3 ресурсы будут использованы полностью, а из 12 ед. 4-го ресурса будет использовано 8.

Задача 26.

Фабрика выпускает три вида тканей, причем суточное плановое задание составляет: не менее 90 м ткани I вида, 70 м – II вида и 60 м III вида. Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на 1 м ткани представлен в таблице. Цена 1м ткани I вида равна 80 ден. ед., II вида – 70 ден. ед., III вида – 60 ден. ед. Определите, сколько метров тканей каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.

Решение. Х₁ – количество ткани I вида (м), Х₂ – II вида, Х₃ – III вида.

F(X)=80X₁+70X₂+60X₃→max

2X₁+3X₂+4X₃≤780

X₁+4X₂+5X₃≤850

3X₁+4X₂+2X₃≤790

X₁≥90

X₂≥70

X₃≥60

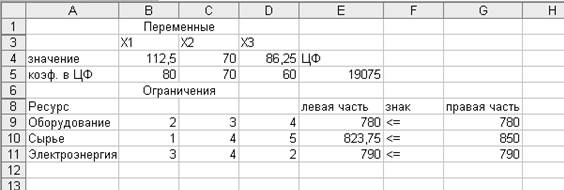
Полученное решение означает, что максимальная общая стоимость выпускаемой продукции 19075 ден. ед. может быть достигнута при выпуске 112,5 м ткани I вида, 70 м – II вида, 86,25 м – III вида. При этом оборудование и электроэнергия используются полностью, а из 850 единиц сырья используется 823,75 единиц.

Задача 29.

Торговое предприятие реализует товары трех групп: А, В. С. Известны нормативы затрат ресурсов в расчете на единицу товара и ограничения по располагаемым ресурсам даны в таблице. Составьте оптимальный план товарооборота по критерию «максимум дохода».

Решение. X₁, X₂, X₃ – Количество товаров А, В, С соответственно.

F(X)=3X₁+5X₂+4X₃→max

0,1X₁+0,2X₂+0,4X₃≤1100

0,05X₁+0,02X₂+0,02X₃≤120

3X₁+X₂+2X₃≤8000

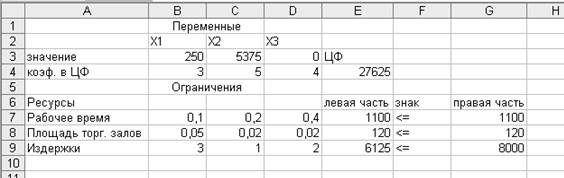
Полученное решение означает, что максимальный доход 27625 руб. предприятие может получить при реализации товара А в размере 250 ед., товара В – 5375, товара С – 0. При этом рабочее время и площадь торговых залов используются полностью, а издержки из 8000 составляют 6125.