§5.
Следствия из аксиом скалярного произведения
1.
Доказательство:
Имеем 
(1). Тогда
Определение
5.1. 
называется длиной вектора 
.
Обозначение:
- длина вектора
.
Таким образом, 
.
2.
. Это вытекает из принятого определения и следствия 1.
3.
, где 
- вектор, противоположный
вектору .
Доказательство:
4.
Для любых и 
имеет место неравенство Коши-Буняковского:
Доказательство.
Рассмотрим
скалярное произведение вектора 
на себя.
Имеем:
(XVI)
где t – любое действительное число. Отсюда на основании аксиом XIII-XV получаем:
Выражение в левой части неравенства
представляет собой квадратный трехчлен относительно t. Так как этот трехчлен должен быть неотрицательным при всех
значениях t, то он не
может иметь двух различных корней и, поэтому, его дискриминант:
Отсюда 
Определение
5.2. Число 
называют косинусом
угла между векторами и .
Итак,
Введение
такого определения оправдывается, в частности, следующими неравенствами: 
Этот
факт непосредственно следует из следствия 4.
5. (Неравенство треугольника)
Доказательство:
Воспользуемся
неравенством Коши-Буняковского:
Откуда: 
Определение 5.3. Векторы и называются ортогональными, если их скалярное произведение
равно 0.
Обозначение: 
- и - ортогональные
векторы.
Итак, 
6. Существуют два ненулевых
ортогональных вектора.
Доказательство:
Пусть
даны два линейно независимых вектора и .
Рассмотрим два вектора: и 
.
Подберем l так,
чтобы 
последнее равенство
последовательно преобразуем так: 
=0 Þ
Таким
образом, векторы 
и 
ортогональны.
В самом
деле:
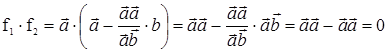
Кроме того, векторы f1 и f2 ненулевые.
7.(Теорема Пифагора). Если векторы и ортогональны, то
Доказательство:
Так как Тогда
Определение
5.4. База 
евклидова пространства
называется ортогональной, если 
для всех 
Если при этом еще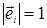 
при 
, то база называется ортонормированной.
8.
Попарно ортогональные ненулевые векторы линейно независимы.
Доказательство:
Пусть векторы 
попарно ортогональны и все отличны от нулевого вектора.
Рассмотрим равенство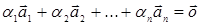 
. Умножая обе части этого равенства последовательно на
векторы , получим:
…………………………………………..
Откуда,
Так
как 
, то из полученных равенств следует a1=a2=…=an=0.
Это означает, что система векторов , линейно независима.
9.
Существуют три ненулевых попарно ортогональных вектора.
Доказательство:
Пусть
и 
два ненулевых
ортогональных вектора, существование которых обеспечено следствием 6. Подберем
ненулевой вектор 
такой, что 
и 
Положим 
, где 
- вектор. Образующий с векторами и в условиях следствия 6 линейно независимую систему. Тогда
Отсюда
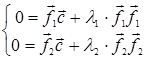
Имеем:
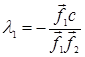и 
Таким образом, отправляясь от трех
линейно независимых векторов 
и 
, мы построили три ненулевых вектора 
, которые попарно ортогональны.
Обобщение. Привлекая
последовательно все базы n-мерного
евклидового пространства, можно построить аналогично следующие системы
ненулевых попарно ортогональных векторов:
…………..
Так как
система векторов линейно независима и
содержит n векторов
(максимальное число линейно независимых векторов), то в результате получена в n-мерном пространстве ортогональная база .
Описанный процесс известен в
математике под названием процесса ортогонализации.
Имея ортогональную базу, нетрудно
получить с ее помощью ортонормированную базу. Для этого вместо каждого вектора
нужно взять вектор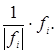 
Убедимся,
что длина этого вектора равна 1. В самом деле,
