§6.2.  Конгруэнтность треугольников

 

Определение 18.7. Если треугольник АВС называется конгруэнтным треугольнику А₁В₁С₁, если

,

.

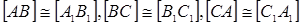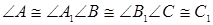Обозначение: 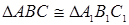 – треугольник АВС называется конгруэнтным треугольнику А₁В₁С₁.

Теорема 18.9. Если 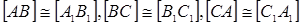, то .

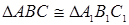Доказательство:

Имеем:

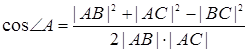,                                             (1)

 

                                        (2)

По условию теоремы .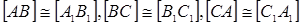

Отсюда и из равенств (1) и (2) следует, что 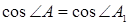, то есть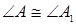

Аналогично устанавливается и соотношения 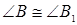, 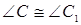. Отсюда .

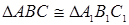Теорема 18.10.   Есл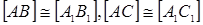и  и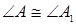   

то .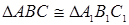

Доказательство:

          На основании теоремы 18.5. имеем:

,

.

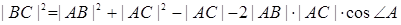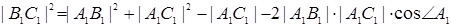Отсюда, учитывая условия теоремы, получим 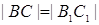, то есть .

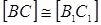На основании предыдущей теоремы .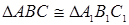

Теорема 18.11. Есл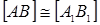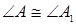и ,  и , .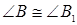

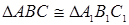Доказательство:

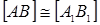Если , то доказанному выше 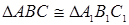. Если 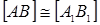, то отложим на луче [АС) от точки А отрезок [А₁С₁] (рис.):

 

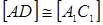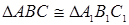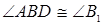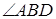. Тогда на основании предыдущей теоремы .  Из конгруэнтности этих треугольников следует, что . Имеем: на луче [ВА) в полуплоскости, содержащей точку С, отложены два угла (различных)  и 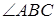, конгруэнтных одному и тому же углу 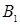. Последнее противоречит теореме 18.4., следовательно  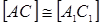и 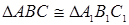.