§3.
Размерность
Определение
3.1. Векторное пространство называется n-мерным, если в нем имеется n линейно
независимых векторов, а всякие n+1 векторы линейно зависимы.
Иначе говоря, размерность векторного пространства – это
максимальное число содержащихся в нем линейно независимых векторов.
Если максимальное число линейно независимых векторов равно
1, то векторное пространство называется одномерным, если это число равно 2,. То
векторное пространство называется двумерным, и т.д.
Векторное пространство, имеющее конечную размерность,
называется конечномерным. Пространство, в котором существует сколь угодно
линейно независимых векторов, называется бесконечномерным.
Определение
3.2. Совокупность n линейно независимых векторов n-мерного
векторного пространства называется его базой.
Теорема 3.1. Каждый вектор 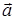 n-мерного векторного пространства можно представить, и притом
единственным образом, в виде линейной комбинации векторов базы.
n-мерного векторного пространства можно представить, и притом
единственным образом, в виде линейной комбинации векторов базы.
Доказательство:
Пусть 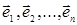 – произвольная база n-мерного
векторного пространства. Так как любые n+1 векторы n-мерного векторного пространства линейно зависимы, то векторы
– произвольная база n-мерного
векторного пространства. Так как любые n+1 векторы n-мерного векторного пространства линейно зависимы, то векторы
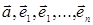 ,
,
линейно зависимы, т.е. нулевой вектор является нетривиальной линейной
комбинацией векторов 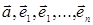 :
:
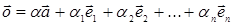 ,
,
где 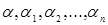 не все равны нулю. При
этом
не все равны нулю. При
этом 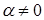 . Если бы
. Если бы  , то тогда среди чисел
, то тогда среди чисел  хотя бы одно было
отлично от нуля, а отсюда следует, что векторы
хотя бы одно было
отлично от нуля, а отсюда следует, что векторы 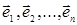 линейно зависимы.
линейно зависимы.
Пусть например, 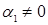 , тогда
, тогда 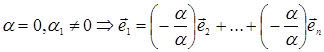 .
.
Откуда следует линейная зависимость векторов 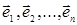 ,
что противоречит условию.
,
что противоречит условию.
Итак, 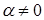 . Если
. Если 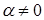 , то
, то
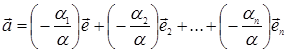
Полученное представление
вектора 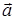 является искомым.
является искомым.
Докажем, что оно единственно.
Допустим, что возможны
два представления вектора 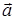 в виде линейной
комбинации базы:
в виде линейной
комбинации базы:
 и
и  .
.
Тогда
 , отсюда
, отсюда
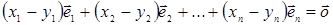 .
.
Так как векторы 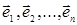 линейно независимы, то
линейно независимы, то
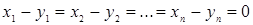
и,
следовательно,
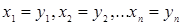 .
.
Ч.т.д.
Примеры.
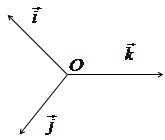 1. Определим размерность векторного
пространства геометрических векторов трехмерного пространства.
1. Определим размерность векторного
пространства геометрических векторов трехмерного пространства.
Докажем, что любые
три вектора 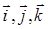 выходящие из одной
точки О и не лежащие в одной плоскости, являются линейно независимыми, а всякие
четыре вектора линейно зависимы.
выходящие из одной
точки О и не лежащие в одной плоскости, являются линейно независимыми, а всякие
четыре вектора линейно зависимы.
 В самом деле, векторы
В самом деле, векторы 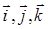 независимы, т.к. в
противном случае один из них, например
независимы, т.к. в
противном случае один из них, например 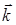 , должен был бы линейно выражаться через два других. Однако
равенство
, должен был бы линейно выражаться через два других. Однако
равенство 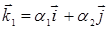 : вектор
: вектор 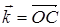 является диагональю
параллелограмма, построенного на
векторах
является диагональю
параллелограмма, построенного на
векторах 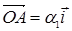 и
и 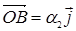 . Отсюда векторы
. Отсюда векторы 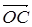 и
и 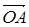 и
и 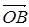 – компланарны, что
противоречит условию их выбора.
– компланарны, что
противоречит условию их выбора.
Докажем теперь, что
любые четыре вектора 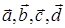 – линейно зависимы.
– линейно зависимы.
Возможны следующие случаи.
а) Векторы 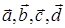 компланарны, тогда
любая тройка векторов линейно зависима. Если система
компланарны, тогда
любая тройка векторов линейно зависима. Если система 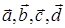 имеет подсистему
линейно зависимых векторов, то эта система линейно зависима.
имеет подсистему
линейно зависимых векторов, то эта система линейно зависима.
б) Из четырех векторов
существует три компланарных, а следовательно, три линейно зависимых вектора.
Как и выше, вся система векторов будет линейно зависимой.
в) Из четырех данных
векторов никакие три не являются компланарными. В этом случае никакие три, а
следовательно, и никакие два вектора из числа данных не являются линейно
зависимыми.
 Пусть
Пусть 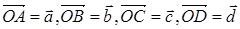 .
.
Обозначим плоскость (OBC) через П1, а плоскость
(AOD) через П2.
(Такие плоскости существуют, так как пара векторов 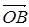 и
и 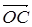 и пара векторов
и пара векторов 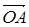 и
и 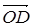 - пары линейно
независимых векторов). Плоскости П1
и П2 имеют общую точку О. Тогда эти плоскости имеют
общую прямую m, проходящую через эту точку О.
- пары линейно
независимых векторов). Плоскости П1
и П2 имеют общую точку О. Тогда эти плоскости имеют
общую прямую m, проходящую через эту точку О.
В плоскости П2 построим
параллелограмм OPDR с диагональю OD. Тогда 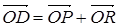 , где
, где 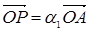 . Вектор
. Вектор 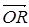 , лежащий в плоскости П1 является линейной
комбинацией векторов
, лежащий в плоскости П1 является линейной
комбинацией векторов 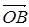 и
и 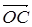 :
: 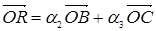 . Тогда
. Тогда 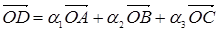 , или
, или 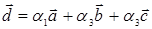 . Отсюда, по теореме 5.1., векторы
. Отсюда, по теореме 5.1., векторы 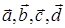 линейно независимы.
линейно независимы.
Итак, множество
геометрических векторов трехмерного евклидового пространства представляет собой
трехмерное векторное пространство.
2. Пространство арифметических
векторов длины n представляет собой n-мерное векторное пространство.
Докажем это.
Прежде всего, нетрудно
установить существование n линейно независимых векторов. Возьмем
векторы:
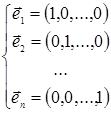
и докажем, что они линейно независимы. В самом деле, если допустить,
что эти векторы линейно зависимы, тогда на основании теоремы 5.1. хотя бы один
из них есть линейная комбинация остальных. Пусть, например, 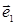 есть линейная
комбинация остальных:
есть линейная
комбинация остальных:
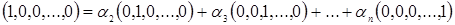 (1)
(1)
тогда
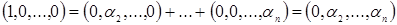 .
.
Отсюда
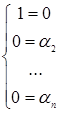 (2)
(2)
Система (2) является
несовместной. Следовательно, не существует такого выбора коэффициентов 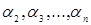 , чтобы равенство (1) удовлетворялось. Таким образом,
линейная независимость системы векторов
, чтобы равенство (1) удовлетворялось. Таким образом,
линейная независимость системы векторов 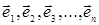 доказана.
доказана.
Докажем теперь, что
всякие n+1 арифметические вектора линейно
зависимы. Пусть имеется система из n+1
векторов:
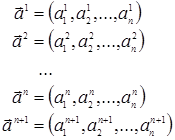
Выясним, существуют ли числа 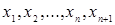 , не все равны нулю, такие, что
, не все равны нулю, такие, что
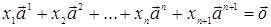 (3)
(3)
Равенство (3) эквивалентно системе:
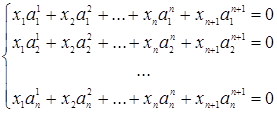 (4)
(4)
Получим систему
однородных уравнений, в которых число уравнений n, а число неизвестных m=n+1. Такая система всегда имеет ненулевое
решение и, следовательно, система
векторов 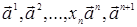 является линейно
зависимой.
является линейно
зависимой.
Контрпример.
Рассмотрим совокупность всех непрерывных функций на
сегменте [0; 1]. Нетрудно убедиться, что в данном случае мы имеем дело с
векторным пространством над полем действительных чисел R. Пусть n – произвольное натуральное число.
Положим:
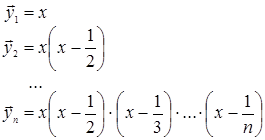
Докажем, что система
векторов 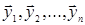 является линейно
независимой. Запишем равенство.
является линейно
независимой. Запишем равенство.
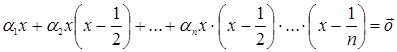 .
.
Положив
последовательно 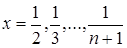 ,
,  , получим
, получим
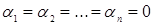
Таким образом, равенство
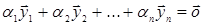
влечет за собой
равенство
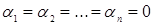
Отсюда, векторы 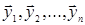 линейно независимы.
Так как n – любое натуральное число, то, следовательно, векторное пространство
всех непрерывных функций заданных на отрезке [0; 1] не имеет конечной системы
линейно независимых векторов, для которых всякая система, содержащая на один
больше векторов, была бы линейно зависима. Поэтому в этом пространстве нельзя
ввести понятие конечной размерности. Такие пространства называются
бесконечными.
линейно независимы.
Так как n – любое натуральное число, то, следовательно, векторное пространство
всех непрерывных функций заданных на отрезке [0; 1] не имеет конечной системы
линейно независимых векторов, для которых всякая система, содержащая на один
больше векторов, была бы линейно зависима. Поэтому в этом пространстве нельзя
ввести понятие конечной размерности. Такие пространства называются
бесконечными.