§4.
Аксиоматика Евклидово-векторного пространства
n-мерное
векторное пространство называется евклидовым, если оно удовлетворяет
дополнительной группе аксиом (называемыми аксиомами скалярного произведения).
Эти аксиомы вводят в n-мерное векторное пространство новое
понятие – понятие скалярного произведения двух векторов.
Аксиомы:
XII. Для любых двух векторов 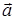 и
и 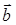 существует единственное число a, называемое их скалярным произведением.
существует единственное число a, называемое их скалярным произведением.
Обозначение: 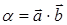 - скалярное произведение векторов
- скалярное произведение векторов 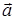 и
и 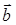 .
.
Таким образом,
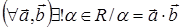
Аксиома XII
утверждает по сути дела, существование отображения VxV®R, ставшего в соответствие каждой паре
векторов единственное число из R.
Это отображение
называется скалярным умножением двух векторов.
XIII. Скалярное умножение двух векторов
коммутативно:
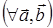
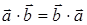
XIV. Скалярное умножение ассоциативно относительно умножения вектора на
число:
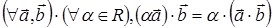
XV. Скалярное умножение диструбутивно относительно сложения векторов:
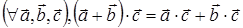
XVI. Для любого вектора 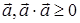 и
и 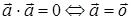
Примеры.
1. рассмотрим трехмерное пространство геометрических
векторов. Под скалярным произведением двух векторов 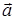 и
и 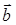 будем понимать число
будем понимать число 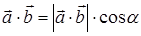 , где
, где 
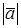 и
и 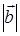 длины векторов
длины векторов 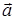 и
и 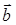 соответственно, а a - угол
между данными векторами.
соответственно, а a - угол
между данными векторами.
Нетрудно установить,
что, определив скалярное произведение таким образом, мы удовлетворим всем
аксиомам скалярного произведения двух векторов. Следовательно, трехмерное
пространство геометрических векторов с введенным таким образом скалярным
произведением является евклидовым.
2. Рассмотрим трехмерное пространство арифметических
векторов. Под скалярным произведением векторов (x1;y1;z1) и (x2;y2;z2) будем понимать число 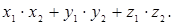 легко можно проверить,
что аксиомы скалярного произведения двух векторов будут удовлетворены.
Следовательно, трехмерное пространство арифметических векторов (с введенным
таким образом скалярным произведением) является евклидовым.
легко можно проверить,
что аксиомы скалярного произведения двух векторов будут удовлетворены.
Следовательно, трехмерное пространство арифметических векторов (с введенным
таким образом скалярным произведением) является евклидовым.
3. Рассмотренный пример можно обобщить на n-мерное
пространство арифметических векторов, если скалярное произведение двух векторов
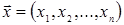 и
и 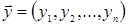 .
.
Определить равенством 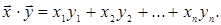 (1)
(1)
Таким образом, n-мерное пространство арифметических
векторов с введенным равенством (1) скалярным произведением, является
евклидовым.