Глава 1
§1.
Аксиоматика векторного пространства
Характеризация
векторного пространства, как математической структуры осуществляются рядом
аксиом.
Основные
понятия теории: "вектор", "сумма двух векторов",
"произведение вектора на действительное число".
Косвенным определением
основных понятий теории векторного пространства являются следующие аксиомы:
I. Для любых векторов 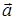 и
и 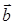 существует единственный третий вектор
существует единственный третий вектор 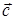 , называемый их суммой
, называемый их суммой
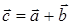
Таким образом
аксиома I постулирует:
а) единственность этой
суммы.
б) существование суммы
двух векторов 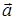 и
и 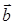 ;
;
Данная аксиома вводит на
множестве векторов V операцию
f1: V x V ® V.
которая называется сложением двух векторов.
II. Сложение векторов коммутативно,
т.е.
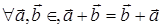 .
.
III. Сложение векторов ассоциативно,
т.е.
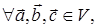

IV. Существует вектор 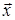 такой, что
такой, что 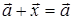 для любого вектора,
для любого вектора, 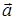 т.е.
т.е.
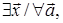
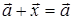
Определение
1.1. Вектор 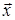 , удовлетворяющий аксиоме IV, называется нулевым вектором и
обозначается
, удовлетворяющий аксиоме IV, называется нулевым вектором и
обозначается 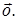
V. Для каждого вектора 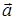 существует такой
вектор
существует такой
вектор 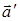 , что
, что 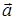 +
+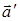 =
=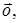
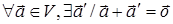

Определение
1.2. Вектор 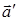 , удовлетворяющий аксиоме V, называется
противоположным вектору
, удовлетворяющий аксиоме V, называется
противоположным вектору 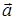 .
.
VI. Для
любого вектора 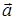 и действительно числа
и действительно числа 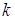 , существует единственный вектор
, существует единственный вектор 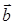 , называемый произведением вектора
, называемый произведением вектора 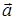 на число
на число 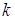 и обозначаемый т.о.:
и обозначаемый т.о.: 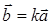 , т.е.
, т.е.
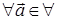 ,
, 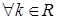 ,
, 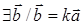
Данная аксиома вводит операция нового
типа (внешнюю операцию):
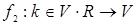
Эта операция носит название «умножение вектора на число».
VII. Для любого вектора 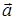 умножение вектора
умножение вектора 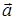 на 1 не изменяет
вектора
на 1 не изменяет
вектора 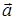 , т.е.
, т.е.
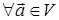 ,
, 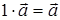
VIII. Умножение вектора на число ассоциативно, т.е.
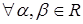 ,
, 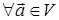 ,
, 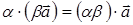
IX. Умножение вектора на число
дистрибутивно сложения чисел, т.е.
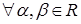 ,
, 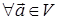 ,
, 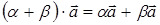
X. Умножение вектора на число
дистрибутивно относительно сложения векторов, т.е.
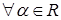 ,
, 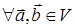 ,
, 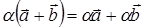
Этим заканчивается
аксиоматика векторного пространства, которое можно теперь определить т.о.:
множество V с
введенными двумя операциями

 ,
,
подчиняющееся аксиомам I-X, называется векторным
пространством над полем действительных чисел R.