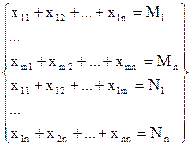Алгоритм получения задачи, двойственной данной

Алгоритм получения задачи, двойственной данной.

Исходя из св-в:

1. число переменных одной задачи = числу ограничений др. задачи.

2. а одной ф-я max-ется , в др. находится min

3. коэф-ты при переменных в выр-нии функции цели одной задачи явл. Равными частями системы ограничений др. задачи.

4. система ограничений одной и др. задачи задается как система неравенств: нер-ва смысла <= при max, нер-ва >= при min

5. матрицы коэф-ов при переменных транспонированы относительно друг друга.

6. условия не отрицательности переменных сохр-ется у той и др. задачи.

Задачи отвечающие св-вам явл. симметричными взаимодвойственными, при этом одну из них наз. Прямой, вторую двойственной.

1. привести прямую задачу к исходной форме. Если в прямой задаче отыскивается max (знаки нер-ва <=) , для двойственной ищем min

2. написать расширенную матрицу прямой з.

3. транспонировать эту матрицу

4. записать условие двойственной задачи.

1 теорема двойственности

(Основная)

Если одна из задач имеет оптимальное решение, то др. задача также имеет оптимальное решение, функции цели = между собой, т.е. fmax=gmin

Если ф-я цели одной из задач не ограниченна, то условие др. з. противоречиво.

2 теорема двойственности

(О дополняющей нежесткости)

Если при подстановке компонентов оптимального плана в систему ограничений исходной задачи i-е ограничение обращается в равенство, то i-я компонента др. з. положительна.

Если i-я компонента дв. з. =0, то i-е ограничение прямой задачи выполняется, как строгое нер-во.

3 теорема двойственности

(Об оценках) (она же 3-св-во ООО)

значения переменных yi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений – нер-в прямой задачи на величину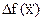

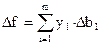
Св-ва Объективно-

обусловленных оценок

2. ООО выступает в качестве показателей степени дефицитности ресурсов. Чем дефицитнее ресурс, тем выше его оценка.

3. величина ООО показывает, как изменяется ф-я цели при увеличении запаса соответствующего ресурса на одну единицу. (с-во справедливо при относительно небольших изменениях запаса ресурсов, т.е. в пределах интервалов устойчивости.)

4. ООО выступает в качестве показателя целесообразности выпуска новых видов изделий.

Понятие о временном ряде

Совокупность значений к-л показателя упорядоченная во времени есть вр.р.

Уровни вр.р. состоят из следующих компонентов:

1. Тренд Ut (долговременная тенденция в изменении показателя)

2. Сезонная компонента St (отображает периодические колебания происходящие в течение года. Вр.р. должен быть задан либо квартальными, либо месячными данными. Сезонность присутствует на транспорте)

3. Циклическая компонента Ct (отражает повторяющееся во времени процесс, но происходящий через ряд лет (урожайность))

4. Остаточная компонента Et (есть часть вр.р. оставшаяся после удаления из него регулярных компонентов: тренда, сезонных и циклических)

Если регулярные комп-ты выделить правильно, то остаточная будет удовлетворять требованиям:

M(E) =0

D(E) const

Последовательные ур-ни ее не коррелированны

Ряд распределения отс. комп. подчиняется норм. закону рапр.

Предварительный анализ вр.р.

Анализ вр.р. начин. С выявления аномальных наблюдений.

Причины вызвавшие аномальные наблюдения:

1. заведомо подготовленные аном. набл.

2. ошибки вызванные неверной передачей статистич. Информации

Подлежат устранения:

1. ошибки второго рода носят объективный хар-р. АН возникшие из-за этих ошибок устранению не подлежат. Для выявления АН используются методы:

метод Ирвина (для каждого уровня ряда начиная со 2-го вычисляют 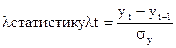где 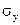- средн. кв. откл. в данном вр.р.

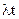сравнивают 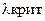(кот. нах. по таблице)

если 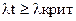, то наблюдение с номером t явл-ся аномальным, в противном случае yt неаном. набл. После обнаружения аном. набл. выясн. его причину.

Методы определение наличия

тренда

1. метод проверки разности средних уровней (метод «Земских статистик»)

вр.р. делится на 2 примерно равные по кол-ву ур-ней части. Для каждой части вычисляют ср. ариф. и дисперсию. Большую дисп. делят на меньшую и получают расчетное значение критерия Фишера. F расч сравнивают с F Крит (из таблицы), если Fрасч <Fкрит, делаем вывод о равенстве дисперсий этих двух частей вр.р.

2. Знаковый критерий Кокса и Стюарта

3. Метод Фостера-Стюарта. Применяют для рядов с любой тенденцией. Для каждого уровня ряда, начиная со второго вычисляются величины: kt и lt. Kt = 1 если yt > всех предыдущих уровней, kt = 0 в ост. случ. Lt =1 если yt < всех пред. Уровней, =0 в ост. случ. Значения величин: st=kt+lt; dt=kt-lt. Находим сумму s и d. t расч для s = 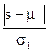; t расч для d = 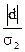, где … табличные значения. Каждое t расч сравн. с t крит. Если t расч для s > t крит. То есть тренд у дисперсии ряда. Если t расч для d > t крит, то есть тренд.

Сглаживание временных рядов

1. Простая скользящая средняя.

Выбирают интервал сглаживания (кол-во ур-ней берут нечетное). 1-й сглаженный уровень придется на середину интервала сглаживания. Недостатки: Ур-ни равноправны по отношению к сглаженному ур-ю; в процедуре сглаживания участвуют не только предыдущие но и последующие ур-ни ряда; теряются p-первых и p – последних уровней ряда, где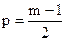

2. Метод взвешенной скользящей средней

Уровни ряда входящие в интервал сглаживания берутся с некоторым определенным весом. Например для m=5 эти веса -3, 12, 17, 12, -3; Для m=3 … 1,2,1. Недостатки те же.

3. Метод экспоненциальной скользящей средней.

Сглаживание свободных от недостатков прост с.с. и взв. с.с. Сглаженный уровень ряда нах по формул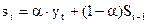е: , где 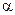параметр сглаживания. 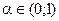принадлежит интервалу, если 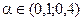явл наилучшим Нах методом подбора.

Хар-ка полиномиальных кривых роста

При помощи кр.р. производится прогнозирование (предсказание поведения показателя в будущем периоде по его поведению в прошлый и настоящий момент). Прогнозирование производится на основании построенной МатМодели вр.ряда.

Yt = a0+a1t. Найдем абсолютные приросты 1-го порядка для ut.

Ut(1)=yt+1-yt=(a0+a1(t+1))-(a0+a1t)=a1=const

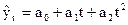абсолютные приросты 1-го порядка линейны относительно t

Найдем абс приросты 2-го порядка (приросты от приростов 1-го порядка)

Ut(2)=ut+1(1)-ut(1)=((a1+a2)+2a2(t+1))-((a1+a2)+2a2t)=2a2=const

Для полинома 2-й степени пост явл-ся абс приросты 2-го порядка

Для полинома k-ой степени пост будут абс приросты k-го порядка

Хар-ка экспоненциальных

кривых роста

Yt=a*b^t (исх уровень)

Yt=k+ ab^t

Для простой экспоненты абс приросты любого порядка зависят от исходного уровня и от t

Для модифицированной k-это предел насыщения, т.е. значение меньше либо больше которого не может быть k определяется либо из прошлого опыта, либо из графика.

Зная k ур-ние модификации экспоненты имеет вид yt-k= ab^t

Хар-ка S-образных кривых роста

Если изменение эк-го показателя хар-ся sобразной кривой, то он в своем развитии проходит 4 этапа:

На 1 э абс приросты отсутствуют; на 2 э возрастают, на 3 постоянны, на 4 уменьшаются.

Из S образных кривых наиболее часто встречаются:

Кривая Гомперца; Кривая Перла-Рида; различные типы логистических кривых.

Выбор наилучшей кривой роста: метод конечных разностей.

м. Тинтнера Суть м.: для данного ряда нах абс приросты 1-го 2-го k-го порядка. Для каждого исходного ряда, а т ж для приростового р вычисляют дисперсию. Каждое очередное вычисленное значение дисперсии сравн с предыдущим. Наилучшим выравнивающим полиномом будет полином k^-1 если S²_k_-1 = S²_k М. Т. позволяет определить наилучш. выравн. кривую только среди полиномиальных кр.

Метод наименьших квадратов

Наилучшей кривой из всех кр явл та, для которой сумма квадратов отклонений исходных значений yt и модельных 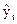значения явл наименьшей. Это принцып наименьших квадратов, леж в основе м. наименьших квадратов

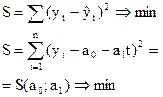
Ф-я S имеет экстремум в той точке, в кот частные производные обращ в 0

Найдем частн произв

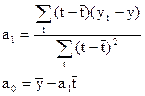
1-й критерий адекватности

Док-ть гипотезу M(E)=0. Для проверки используем .

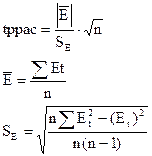
S – ср квадр-е откл-е в ряду значений остаточной компоненты

Если t расч < t крит=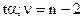 то гипотеза принимается

2-й критерий адекватности

(критерий поворотных точек)

т.п. – это значение остаточной компоненты Et, если оно одновременно >2-х соседних значений, либо < них. При пом 2-го крит проверяется случайность ряда значений Et.. В случайном ряду число п.т. p удовлетворяет нер-ву

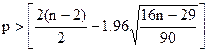полученное значение не округляется!!!

3-й критерий адекватности

(критерий Дарбина-Уотсона)

Проверяется независимость последовательных уровней Et

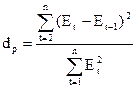
d расч сравн с двумя крит-ми уровнями. Знач-я крит-х ур-ней зависят от длины вр. р.

I-уровни зависимы; II – критерий не дает ответа; III – уровни независимы

I II III

0 0,8 1,36 2

Если dp>2, то треб доп исследование dp’=4-dp (больше 4-х не бывает)

r(1)-1-й коэффициент автокорреляции

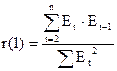если r(1) <0.36, то ур-ни независимы.

4-й критерий адекватности

(R/S критерий)

проверяется: соответствует ли ряд распределения Et нормальному закону. Для этого

Если R/S расч попадает в пром от (2,7;3,7), то Et распределяется по норм закону.

Точность модели

Определяется по величине средней относительной ошибки

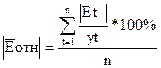Если <=5% модель точна;

5%<=E отн <=10% - модель удовл; E отн > 10% - модельне точна

Прогнозирование при помощи кривой роста

Для получения прогнозных значений подставим в модель вместо t последующие значения. k-шаг прогноза; t=n+k (точечный прогноз)

Вероятность того, что точечный прогноз сбудется =0, поэтому строим интервальный прогноз. uk-ширина доверительного интервала

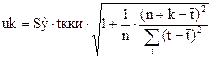где Sy – средняя квадр ош модели

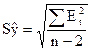t крит =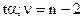

Точечный интервальный прогноз по м. Брауна

М. Б. не учитывает сезонную и циклическую компоненты (в ней только тренд и Et)

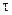Для прогнозирования используем ур-ние с последнего шага. = а₀+а₁, при 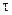=1, =2 (точечный прогноз)

Для интервального прогноза нужно рассчитать ширину доверительного интервала

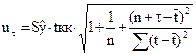
где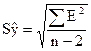

Определение начальных

параметров модели Брауна

М. Б. не учитывает сезонную и циклическую компоненты (в ней только тренд и Et)

Пересчет параметров осущ по формулам

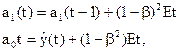где B коэфф дисконтирования данных. Наилучшее B (0,1;0,4)

Модель на начальном шаге имела вид 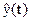=а₀+а₁t

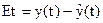, а0 и а1 берем из предыстории

Канонический вид ЗЛП

ЗЛП назыв заданной в каноническом виде, если система ограничений ее явл системой ур-ний с неотриц правыми частыми. Любое нер-во можно привести к ур-нию путем введения в него любой дополнительной неотрицательной переменной.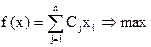

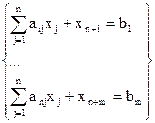xj>=0; j=1

Графический метод решения ЗЛП

Необходимо:

1. построить множество решений сис ограничений. В общем случае реш-ем явл выпуклый многоугольник n-мерного пространства. Любая точка многоуг-ка явл допустимым решением.

Находим оптимальный план. Точки многоугольника в кот ф-я цель принимает к-л определенное значение f(x)=a. Эти точки располагаем на прямой наз. линией уровня. При f(x)=а линия уровня пройдет параллельно (0;0). Имея 2-е линии уровня достаточно, чтобы определить направление вектора-градиента. Перемещаем лин уровня до той

Особые случаи решения ЗЛП

графически

1. оптимальное решение задачи единственно

2. оптимальное решение существует и не одно

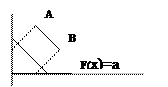fmax=f(А)=f(B)=f(AB)

3. ф-я-цель не ограничена

4. Если у многоугольника решений нет, то система противоречива, следовательно ЗЛП противоречива

Соотношение между угловыми точками множества допустимых решений ЗЛП…

Между угл точками множ доп решений системы лин-х нер-в и допуст базисн реш соот сис лин Ур-ний сущ-ет взаимно однозначное соотвествие: Каждому допуст базисн решению соответствует угловая точка. Каждый угловой точке соответствует базисное решение допустимое.

Транспортная задача

Пусть в m пунктах отправления сосредоточен однородный груз, кот надо доставить в n пунктов назначения. Известны мощности каждого поставщика и спрос каждого потребителя ( r), показатели затрат (aj) на перевозку ед груза от поставщика (i) к потребителю (j).

Открытая и закрытая модели транспортной задачи

Если 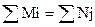задача закрытая

Если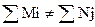 задача открытая

Любую открытую задачу сводим к закрытой путем введения фиктивного поставщика и потребителя. Mi-мощность поставщика, Nj-спрос потребителя

Mф=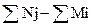

Особенности математической модели транспортной задачи

Пусть задача закрытая, напишем мат модель. Обозначим кол-во груза перевез поставщиком I к потребителю j через xij

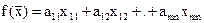достав бы min значением ф-ции f(x) и удовлетв системе ограничений