Задача 

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн руб.) от объема капиталовложений (Х, млн руб.).

Х	12	4	18	27	26	29	1	13	26	5
Y	21	10	26	33	34	37	9	21	32	14

Требуется:

1.  Найти параметры уравнения линейной регрессии, дать экономическую  интерпретацию коэффициента регрессии.

2.   Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.

3.  Проверить выполнение предпосылок  МНК.

4.  Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).

5.  Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве  модели.

6.  Осуществить прогнозирование  среднего значения  показателя Y при уровне  значимости  α=0,1,  если  прогнозное значение фактора Х составит 80% от его максимального значения.

7.  Представить графически фактические и модельные значения Y точки прогноза.

8.  Составить уравнения нелинейной регрессии:

·   гиперболической;

·   степенной;

·   показательной.

Привести графики построенных уравнений регрессии.

9.  Для указанных моделей найти  коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам  и сделать вывод.

Решение

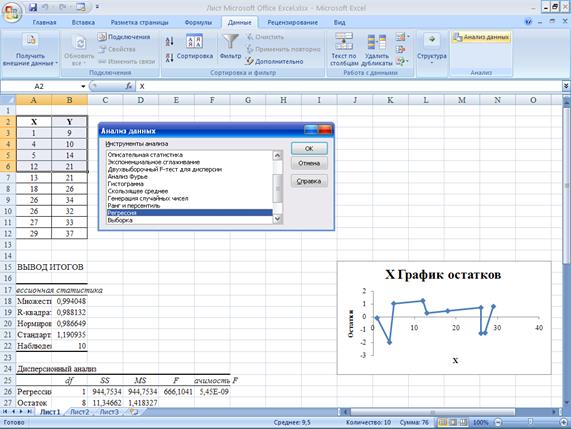
1.  Расчет параметров уравнения линейной регрессии проводится с помощью инструмента анализа данных в Excel. Однако мы видим, что сначала необходимо отсортировать исходные данные по возрастанию переменной Х, так как в задании присутствует необходимость проверки предпосылок МНК.

Выполним сортировку: Данные – Сортировка – По переменной Х – По возрастанию:

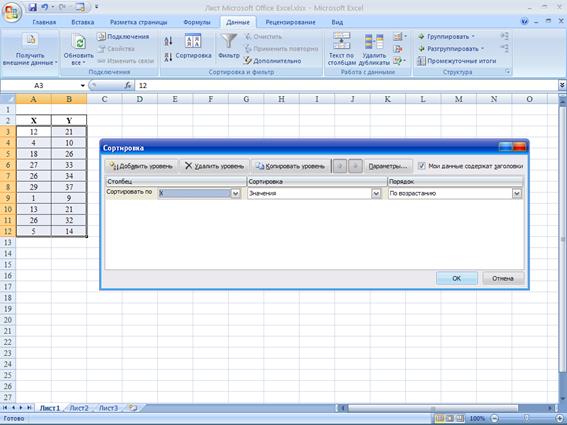
Получим:

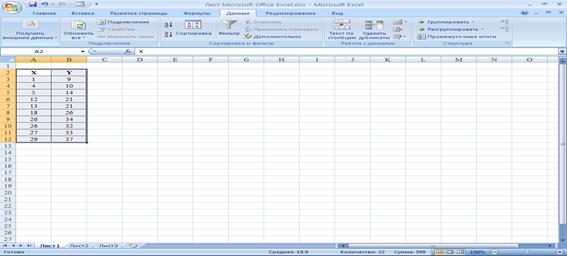
Далее выполним: Анализ данных – Регрессия:

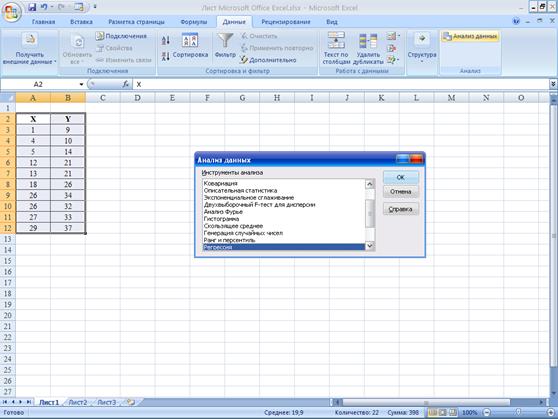
Далее введем входные интервалы для Х и Y, поставим галочку на Метки, осуществим запрос на остатки и график остатков:

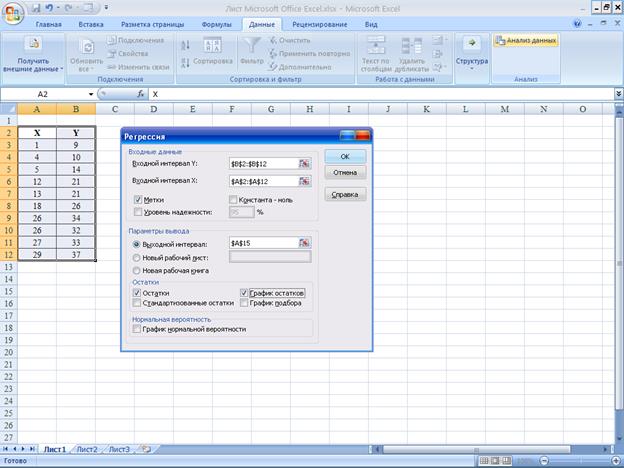
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,994048
R-квадрат	0,988132
Нормированный R-квадрат	0,986649
Стандартная ошибка	1,190935
Наблюдения	10
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	944,7534	944,7534	666,1041	5,45E-09
Остаток	8	11,34662	1,418327
Итого	9	956,1
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	8,12023	0,711501	11,41281	3,14E-06	6,479505	9,760955	6,479505	9,760955
X	0,967688	0,037494	25,80899	5,45E-09	0,881226	1,054149	0,881226	1,054149

Результат регрессионного анализа имеет вид:

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
1	9,087918	-0,08792
2	11,99098	-1,99098
3	12,95867	1,041332
4	19,73248	1,267519
5	20,70017	0,299831
6	25,53861	0,461394
7	33,28011	0,719893
8	33,28011	-1,28011
9	34,24779	-1,24779
10	36,18317	0,81683

Таким образом, исходя из коэффициентов, получаем уравнение зависимости объема выпуска продукции от объема капиталовложений:

Y=8,12+0,97Х.

С увеличением объема капиталовложений на 1 млн руб. объем выпускаемой продукции увеличится в среднем на 970 тыс. руб.

2.     Остатки получены по итогам регрессии:

Остатки
-0,08792
-1,99098
1,041332
1,267519
0,299831
0,461394
0,719893
-1,28011
-1,24779
0,81683

 

Остаточная сумма квадратов равна 11,35 (столбец SS остатка в табл. «Дисперсионный анализ»).

Дисперсия остатков S_ε²=1,42 (столбец MS остатка в табл. «Дисперсионный анализ).

График остатков ранее уже был получен. Для удобства преобразуем его в точечную диаграмму, соединив точки:

3.  1)  Проверим выполнение свойства случайности остатков построенной модели  зависимости объемов выпуска продукции от объема капиталовложений. Проверку осуществим с помощью критерия поворотных точек. По графику остатков видно, что количество поворотов p=5. При n=10,

p_кр=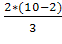 – 1,96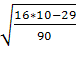={2,9}=2.

P=5>p_кр=2, следовательно, свойство случайности для ряда остатков выполняется.

2) Свойство нулевого математического ожидания для линейной модели выполняется автоматически.

3) Проверим выполнение свойства постоянной дисперсии остаточной компоненты с помощью критерия Голдфельда – Квандта. Возьмем первые и последние четыре уровня, средние два уровня не рассматриваем. С помощью функции Регрессия построим модели по первым и последним четырем наблюдениям:

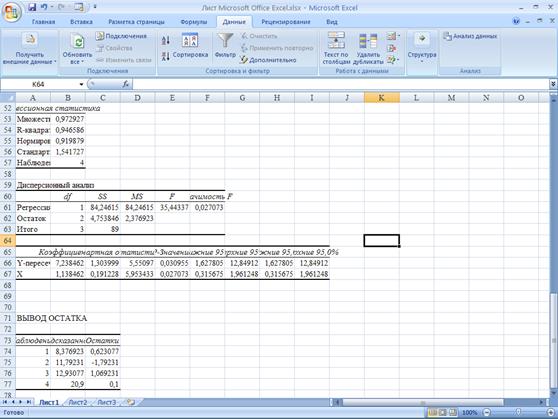
Итоги регрессии для первых четырех наблюдений:

Итоги регрессии для последних четырех наблюдений:

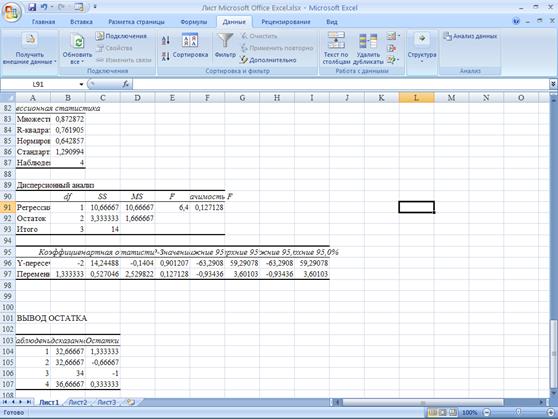
Для первой модели SS₁=4,75; для второй модели SS₂=3,33.

F= 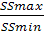==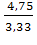1,43.

Критическое значение F_кр при α=5% и числах степеней свободы

k₁=k₂=4-1-1=2 найдем с помощью функции FРАСПОБР:

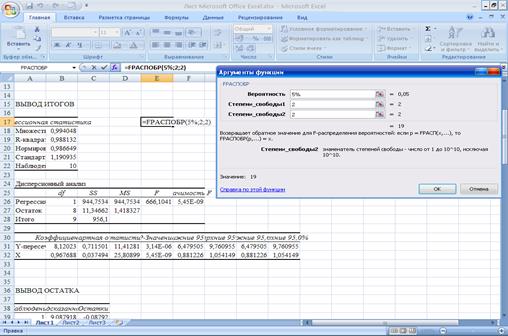
Получили, что F_кр=19.

F=1,43<F_кр=19, следовательно, свойство постоянной дисперсии остаточной компоненты выполняется, модель гомоскедастичная.

4) Проверим выполнение свойства независимости остатков, используя критерий Дарбина – Уотсона.

Вычислим d-статистику с помощью функций СУММКВ и СУММКВРАЗН:

	СУММКВРАЗН(Е)=		22,16079
	СУММКВ(Е)=	11,34662
	d=		1,953075

Определим критические уровни d₁ и d₂ при n=10 по таблице. Получим, d₁=0,88 и d₂=1,32. Таким образом, d больше верхнего критического уровня и меньше 2, а это говорит о том, что свойство независимости остаточной компоненты выполняется.

5) Проверим выполнение свойства нормального распределения остатков, используя R/S критерий.

R/S=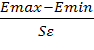= 2,736084.

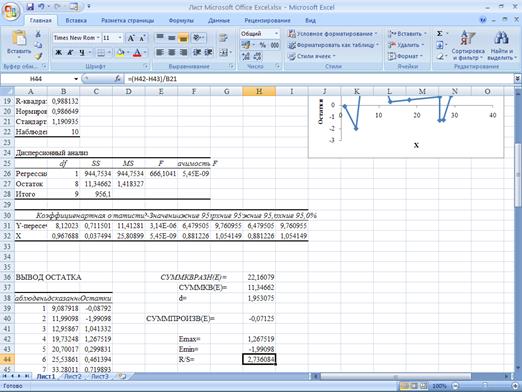
Критический интервал при n=10 и α=5% будет (2,67;3,57).

2,74Є(2,67;3,57), следовательно, свойство нормального распределения остатков для построенной модели выполняется.

Проведенная проверка предпосылок регрессионного анализа показала, что для модели выполняются все условия Гаусса – Маркова. Таким образом, МНК – наилучший метод моделирования.

4.  Выпишем из Регрессии t-статистику для коэффициентов модели:

а=8,12; t(a)=11,41

b=0,97; t(b)=25,81 (столбец « t-статистик» Регрессии).

Определим t_кр с помощью функции СТЬЮДРАСПОБР(5%; 8):

t_кр=2,31.

Сравним |t(a)|=11,41>t_кр=2,31, следовательно, свободный коэффициент является значимым, его необходимо сохранить в модели.

|t(b)|=25,81>t_кр=2,31, следовательно, коэффициент регрессии b является значимым, его и фактор объема капиталовложений нужно также сохранить в модели.

Оба коэффициента являются значимыми и необходимыми в данной модели.

5.  Выпишем из Регрессии R²=0,99=99%.

Таким образом, вариация объема выпуска продукции Y на 99% объясняется по полученному уравнению вариацией объема капиталовложений.

Оценим значимость уравнения с помощью F-критерия Фишера.

Выпишем из Регрессии F=666,1.

Fкр=5,32,  найдем с помощью функции FРАСПОБР(5%; k₁=1; k₂=8):

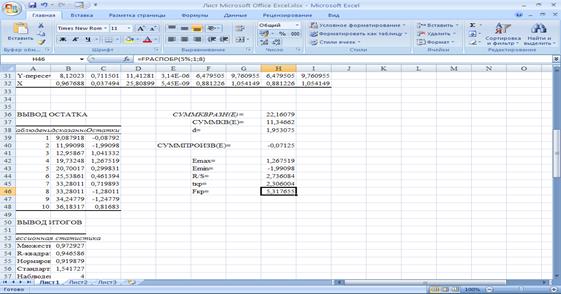
Сравним F=666,1>F_кр=5,32, следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенной в модель факторной переменной X.

Найдем теперь среднюю относительную ошибку аппроксимации. Для этого используем исходные значения Y_i и найденные Регрессией остатки E_i. Вычислим относительные погрешности: Е_отн=|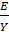|*100%:

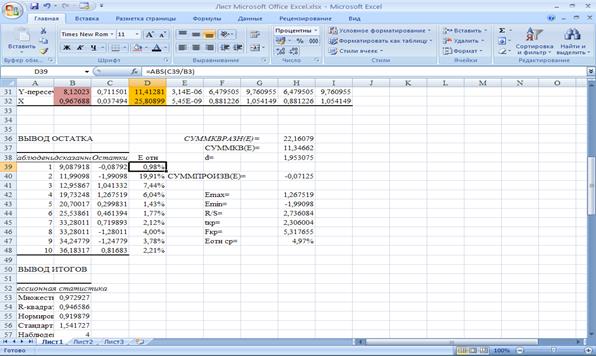
С помощью СРЗНАЧ найдем Е_отн=4,97%.

Сравним Е_отн=4,97%Є(0; 5%), следовательно, модель является достаточно точной, однако точность модели приближена к удовлетворительной.

Вывод: в результате исследования получилось, что все коэффициенты модели, а также сама модель являются значимыми, что свидетельствует об адекватности модели, о том, что ее можно использовать как для анализа, так и для прогнозирования. Модель также является достаточно точной.

 

6.  Для прогнозирования найдем прогнозное значение Х. В задаче сказано, что оно составляет 80% от его максимального значения. Используя функцию МАКС, получим что Х_max=29, а 80% от 29 равно 23,2. Таким образом, Х^*=23,2. Найдем ожидаемый объем выпуска продукции Y_т^*=8,12+0,97*23,2=30,624 (млн руб.)

Для интервального прогноза подготовим:

- стандартная ошибка модели S_ε=1,19 (стандартная ошибка в Регрессии);

- среднее значение х=16,1 (СРЗНАЧ по Х);

- ∑(х_i-x)²=1008,9 (КВАДРОТКЛ по Х).

Стандартная ошибка прогнозирования составит:

S(Y_т^*)=1,19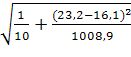=0,461:

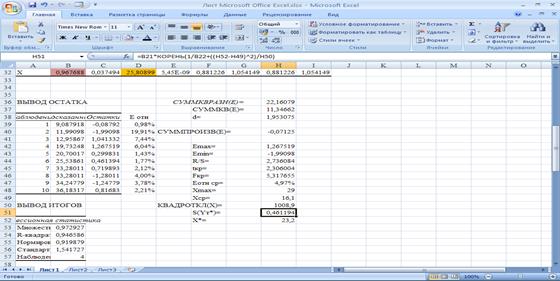
При t_кр (10%;8)=1,86 в рамках доверительного интервала U(Y_т^*)= S(Y_т^*)* t_кр=0,461*1,86=0,858.

Границы интервала будут:

U_нижн=30,624-0,858=29,766;

U_верх=30,624+0,858=31,482.

Таким образом, с надежностью 90% можно утверждать, что объем выпуска продукции будет составлять от 29,766 до 31,482 млн руб.

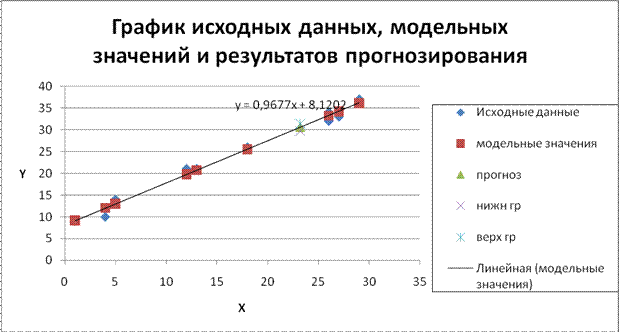
7.  Для построения данного графика была выбрана диаграмма точечного типа. На графике представлены исходные значения Х и Y, теоретические (смоделированные) значения Y, а также результаты точечного и интервального прогноза. Была добавлена и линия тренда (прямая по модельным значениям Y).

8.  Теперь составим уравнения нелинейной регрессии и приведем графики для составленных уравнений.

1)  Построим степенную модель. Отобразим для этого исходные данные в виде точечной диаграммы, а затем добавим линию степенного тренда:

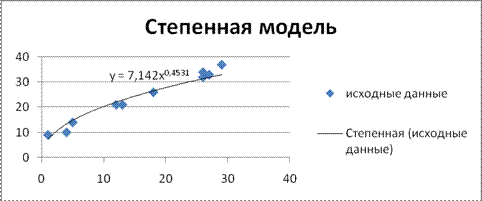
Получили уравнение степенной модели: Y=7,142.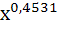

2)  Построим показательную модель. Отобразим для этого исходные данные в виде точечной диаграммы, а затем добавим линию экспоненциального тренда.

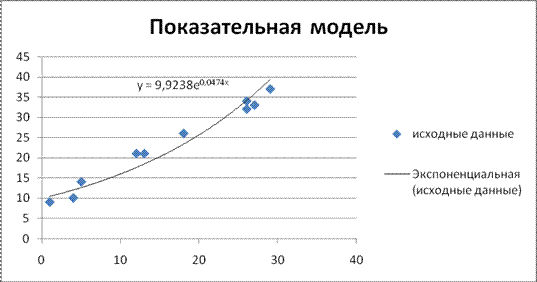
Получили уравнение модели Y=9,9238.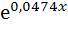

3)  Гиперболическая модель Y=a+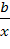 не является стандартной в отличие от степенной и показательной моделей, а, значит, ее нельзя построить обычным стандартным способом. Добавим новую переменную x=, тогда Y=а+b*x.

С помощью Регрессии получим коэффициенты линейной модели Y=а+b*x:

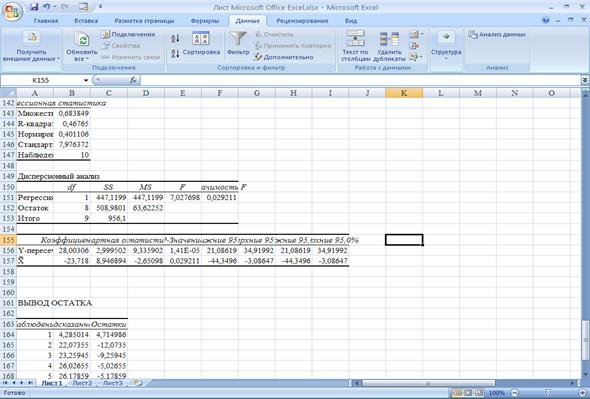
а=28; b=-23,72. Получено уравнение гиперболической модели:

Y=28-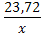. Для построения графика добавим к ряду исходных данных (х_i;y_i) ряд теоретических значений (x_i;y_т):

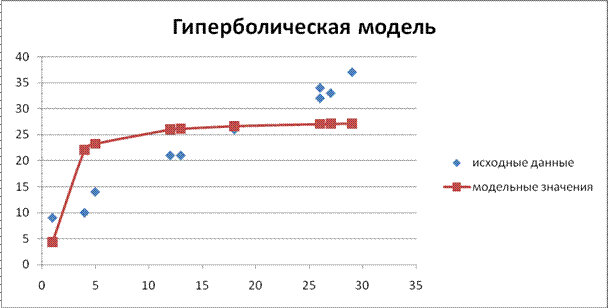
9.  Теперь для всех трех нелинейных моделей найдем коэффициенты детерминации, эластичности и средние относительные ошибки аппроксимации.

По полученным данным сделаем вывод, выберем наилучшую модель. Заполним вспомогательную расчетную таблицу для каждой нелинейной модели:

	у=7,142х^0,4531
X	Y	Yт	Е	Еотн
1	9	7,142	1,858	20,64%
4	10	13,38484	-3,38484	33,85%
5	14	14,80891	-0,80891	5,78%	СУММКВ(Е)=	46,98487
12	21	22,01896	-1,01896	4,85%	КВАДРОТКЛ(Y)=	956,1
13	21	22,83219	-1,83219	8,72%	R-квадрат=	0,950858
18	26	26,45963	-0,45963	1,77%
26	34	31,25678	2,743218	8,07%
26	32	31,25678	0,743218	2,32%
27	33	31,79587	1,204126	3,65%
29	37	32,84221	4,15779	11,24%
			Еотн ср	10,09%
у=9,9238е^0,0447х	b=е^0,0447=	1,045714
X	Y	Yт	Е	Еотн
1	9	10,37746	-1,37746	15,31%
4	10	11,8667	-1,8667	18,67%
5	14	12,40917	1,590828	11,36%	СУММКВ(Е)=	55,10299
12	21	16,96811	4,031886	19,20%	КВАДРОТКЛ(Y)=	956,1
13	21	17,7438	3,256204	15,51%	R-квадрат=	0,942367
18	26	22,18765	3,812348	14,66%
26	34	31,72598	2,27402	6,69%
26	32	31,72598	0,27402	0,86%
27	33	33,1763	-0,1763	0,53%
29	37	36,27889	0,721114	1,95%
			Еотн ср	10,47%
	у=28-23,72/х
X	Y	Yт	Е	Еотн
1	9	4,28	4,72	52,44%
4	10	22,07	-12,07	120,70%
5	14	23,256	-9,256	66,11%	СУММКВ(Е)=	508,9803
12	21	26,02333	-5,02333	23,92%	КВАДРОТКЛ(Y)=	956,1
13	21	26,17538	-5,17538	24,64%	R-квадрат=	0,46765
18	26	26,68222	-0,68222	2,62%
26	34	27,08769	6,912308	20,33%
26	32	27,08769	4,912308	15,35%
27	33	27,12148	5,878519	17,81%
29	37	27,18207	9,817931	26,53%
			Еотн ср	37,05%

Для вычисления индекса детерминации подготовили:

∑Е² (СУММКВ для столбцов ошибок);

∑(y-y)² (КВАДРОТКЛ для Y);

R² =1-.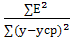

Составим итоговую сводную таблицу характеристик качества построенных моделей:

Модель	Еотн ср	R-квадрат
Степенная	10,09%	0,9508578
Показательная	10,47%	0,9423669
Гиперболическая	37,05%	0,4676496

Теперь для всех трех построенных моделей найдем коэффициенты эластичности.

Для степенной модели Y=7,142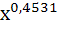 коэффициент эластичности (Э) – величина постоянная. В данном случае она равна 0,45. Это означает, сто увеличение объема капиталовложений на 1% приведет к увеличению объема выпуска продукции на 0,45%.

Для показательной (Y=a*b^x)  Э=x*ln b и гиперболической (Y=a+b/x)   Э=- 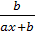 моделей коэффициенты эластичности представлены в таблице:

Х	коэффициенты эластичности
показ	гипербол
1	0,0447	5,5420561
4	0,1788	0,2686905
5	0,2235	0,2039904

Таким образом, согласно показательной модели, увеличение объема капиталовложений на 1% приводит к увеличению объема выпуска продукции на величину от 0,04% до 0,22% (с возрастанием Х его влияние на Y усиливается).

Согласно гиперболической модели, при увеличении объема капиталовложений на 1%  происходит увеличение объема выпуска продукции от 5,54% до 0,2% (с возрастанием Х его влияние на Y ослабевает).

Вывод: Проанализировав найденные средние относительные ошибки аппроксимации для всех трех нелинейных моделей, можно сделать вывод, что наиболее точной является степенная модель, так как ее точность является удовлетворительной и ее средняя относительная ошибка аппроксимации (Е_{отн ср}=10,09%) является наименьшей из всех трех моделей. Что касается индекса детерминации, то опять же наилучшей моделью является степенная, так как в ней вариация объема выпуска продукции Y учтена на 95% (R² наибольший из всех трех моделей). Таким образом, как  для прогноза, так и для анализа степенная модель из трех построенных подходит наилучшим образом, а гиперболическая модель не подходит ни для описания данной зависимости объема выпуска продукции от объема капиталовложений, ни для прогнозирования. Рассмотрев коэффициенты эластичности,  можно также отметить непригодность гиперболической модели. Что касается показательной модели, то по своим характеристикам она близка к степенной и может быть использована для анализа и прогноза.