Имеются данные о деятельности
крупнейших компаний США в 1996
г. (табл. 1).
Таблица 1
|
п/n
|
Чистый
доход, млрд. долл. США
|
Оборот капитала, млрд. долл. США
|
Использованный
капитал, млрд. долл.
|
Численность служащих, тыс. чел.
|
Рыночная капитализация компании, млрд. долл. США
|
|
Y
|
X1
|
X2
|
X3
|
X4
|
|
1
|
0,9
|
31,3
|
18,9
|
43,0
|
40,9
|
|
2
|
1,7
|
13,4
|
13,7
|
64,7
|
40,5
|
…………………………………………………………………..
|
25
|
0,7
|
15,5
|
5,8
|
80,8
|
27,2
|
Задание
1.
Рассчитайте
матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов
корреляции.
2.
Рассчитайте
параметры линейного уравнения множественной регрессии с полным перечнем
факторов.
3.
Оцените
статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о
значимости уравнения проверьте с помощью F-критерия; оцените качество
уравнения регрессии с помощью
коэффициента детерминации 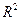 .
.
4.
Дайте
сравнительную оценку силы связи факторов с результатом с помощью коэффициентов
эластичности, 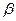 и
и 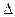 коэффициентов.
коэффициентов.
5.
Оцените
точность уравнения через среднюю относительную ошибку аппроксимации.
6.
Отберите
информативные факторы в модель по t-критерию для коэффициентов
регрессии. Постройте модель только с
информативными факторами и оцените ее параметры.
7.
Рассчитайте
прогнозное значение результата, если прогнозные значения факторов составляют
80% от их максимальных значений.
8.
Рассчитайте
ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а =
0,05; а = 0,10).
1.Использование
инструмента Корреляция (Анализ
данных в EXCEL).
Для проведения корреляционного анализа выполните
следующие действия:
·
Данные для корреляционного анализа должны
располагаться в смежных диапазонах ячеек.
·
Выберите команду СервисÞАнализ данных.
·
В диалоговом окне Анализ данных выберите
инструмент Корреляция, а затем
щелкните на кнопке ОК.
·
В диалоговом окне Корреляця в поле Входной интервал необходимо ввести диапазон ячеек,
содержащих исходные данные (выбираем $B$7:$F$32). Если выделены и заголовки
столбцов, то установить флажок Метки в первой строке.
·
Выберите параметры вывода.
·
ОК.
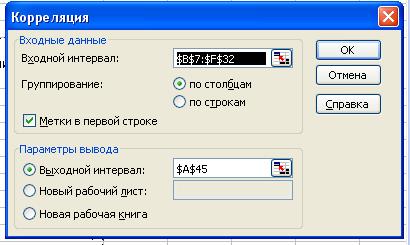
Рис.1 Диалоговое окно Корреляция
Таблица 1.
Результат корреляционного анализа.
|
|
Чистый доход, Y
|
Оборот капитала, X1
|
Использо-ванный капитал, X2
|
Числен-ность служа-щих, X3
|
Рыночная капитализация компании, X4
|
|
Чистый до-ход, Y
|
1
|
|
|
|
|
|
Оборот капитала, X1
|
0,848
|
1
|
|
|
|
|
Использованный капитал, X2
|
0,763
|
0,898
|
1
|
|
|
|
Численность служащих, X3
|
0,830
|
0,912
|
0,713
|
1
|
|
|
Рыночная капитализация компании,
X4
|
0,269
|
0,249
|
0,348
|
0,115
|
1
|
Анализ матрицы
коэффициентов парной корреляции показывает, что зависимая переменная У имеет
тесную связь с Х1 (ryx1=0,848), с Х2 (ryx2=0.763), X3 (ryx3=0.830). Однако факторы X3 и X1 тесно связаны между собой (rx1x3=0.912), что
свидетельствует о наличие мультиколлинеарности.
ryxi>rxixk r yx1>r x1x3
r yx1>r x1x2
ryxk>rxixk 0,848>0,912 не верно 0,848>0,898 не верно
rxixk<0,8 r yx3> r x1x3
r yx2>r x1x2
0,830>0,912 не верно 0,763>0,898 не верно
r x1x3<0,8 r x1x2 <0,8
0,912<0,8 не верно 0,898<0,8 не верно
Если приведенные неравенства (или хотя бы одно из них) не
выполняются, то в модель включают тот фактор, который наиболее тесно связан с
У.
Оценим
значимость коэффициента корреляции. Для этого рассчитаем значение t-статистики по формуле
t расч = (r2/(1-r2)(n-2))/^(1/2)
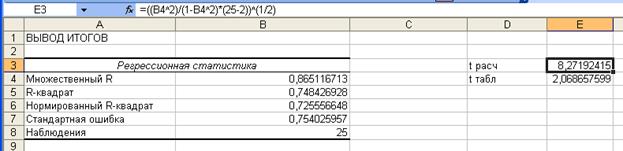
Рис.2 Фрагмент рабочего листа Excel
Табличное значение критерия Стьюдента можно найти с
помощью функции СТЬЮДРАСПОБР: t табл(уровень
значимости равен 0,05; число степеней свободы k=25-2) = 2,068.
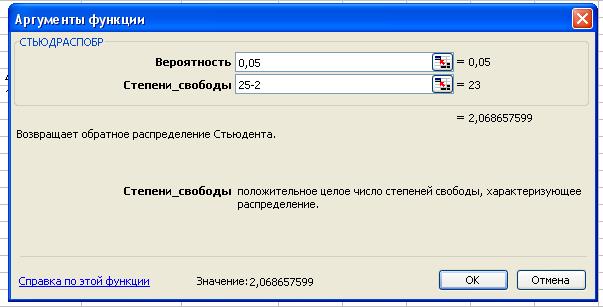
Рис.3 Фрагмент рабочего листа Excel
Сравнивая числовые значения критериев, видно, что
t расч> t табл , т.е. полученное значение коэффициента
корреляции значимо.
2.
Для проведения регрессионного анализа выполните
следующие действия:
·
Выберите команду СервисÞАнализ данных.
·
В диалоговом окне Анализ данных выберите
инструмент Регрессия, а затем
щелкните на кнопке ОК
·
В диалоговом окне Регрессия в поле Входной интервал Y введите адрес
одного диапазона ячеек, который
представляет зависимую переменную ($B$7:$B$32). В поле Входной
интервал Х введите адреса одного или нескольких диапазонов, которые
содержат значения независимых переменных ($C$7:$F$32) (Рисунок 1.).
·
Если выделены и заголовки столбцов, то установить
флажок Метки
в первой строке.
·
Выберите параметры вывода. В данном примере Новая
рабочая книга
·
В поле Остатки поставьте необходимые
флажки.
·
ОК.
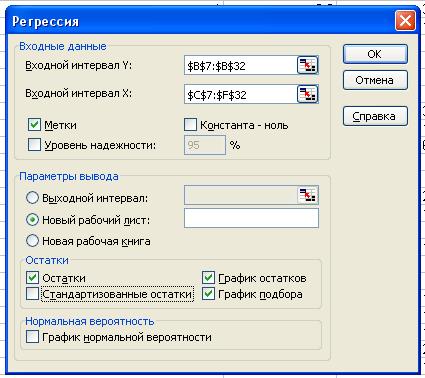
Рисунок
4. Диалоговое окно Регрессия подготовлено
к выполнению анализа данных.
Результат регрессионного анализа содержится в таблицах 1
–3. Рассмотрим содержание этих таблиц.
|
Регрессионная
статистика
|
|
Множественный
R
|
0,869743924
|
|
R-квадрат
|
0,756454493
|
|
Нормированный
R-квадрат
|
0,707745392
|
|
Стандартная
ошибка
|
0,77810933
|
|
Наблюдения
|
25
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
4
|
37,6109174
|
9,402729351
|
15,53004412
|
6,2879E-06
|
|
Остаток
|
20
|
12,1090826
|
0,60545413
|
|
|
|
Итого
|
24
|
49,72
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
-0,362521945
|
1,191933731
|
-0,304146057
|
|
Оборот
капитала, X1
|
0,003502997
|
0,019577778
|
0,178927183
|
|
Использо-ванный
ка-питал, X2
|
0,017414898
|
0,021687383
|
0,802996741
|
|
Числен-ность
служа-щих, X3
|
0,005335038
|
0,003215755
|
1,659031404
|
|
Рыночная
ка-питализация ком-пании, X4
|
0,02862124
|
0,036582896
|
0,782366704
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное
Чистый до-ход, Y
|
Остатки
|
|
1
|
1,476278764
|
-0,576278764
|
|
2
|
1,427339482
|
0,272660518
|
|
3
|
1,216824293
|
-0,516824293
|
|
4
|
1,125836172
|
0,574163828
|
|
5
|
1,720269033
|
0,879730967
|
|
6
|
1,064856936
|
0,235143064
|
|
7
|
4,752057832
|
-0,652057832
|
|
8
|
1,560162019
|
0,039837981
|
|
9
|
6,285770796
|
0,614229204
|
|
10
|
0,701068329
|
-0,301068329
|
|
11
|
0,953926401
|
0,346073599
|
|
12
|
1,291100351
|
0,608899649
|
|
13
|
0,993876693
|
0,906123307
|
|
14
|
1,969626222
|
-0,569626222
|
|
15
|
1,414341773
|
-1,014341773
|
|
16
|
0,814491677
|
-0,014491677
|
|
17
|
1,588975843
|
0,211024157
|
|
18
|
1,166154601
|
-0,266154601
|
|
19
|
1,43458937
|
-0,33458937
|
|
20
|
1,044173477
|
0,855826523
|
|
21
|
1,274936197
|
-2,174936197
|
|
22
|
1,04746402
|
0,25253598
|
|
23
|
1,066479099
|
0,933520901
|
|
24
|
0,607050917
|
-0,007050917
|
|
25
|
1,002349703
|
-0,302349703
|
Уравнение
регрессии можно записать в следующем
виде:
y = -0,362 + 0,003х1 + 0.017x2 +0.005х3
+ 0,028х4
3. Оценим статистическую значимость
параметров регрессионной модели с помощью t-критерия:
Значимость
коэффициентов уравнения регрессии оценим с использованием t-критерия Стьюдента.
ta0 = -0,304
ta1 = 0,1789
ta2 = 0,8029
ta3 = 1,659
ta4 = 0,7823
Расчетные значения
t-критерия Стьюдента для коэффициентов уравнения регрессии приведены в
четвертом столбце таблицы 7 протокола EXCEL.
Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР
Табличное значение
t-критерия при 5% уровне значимости и степенях свободы (25-4-1=20) составляет 2.08
При α=0,2
табличное значение t-критерия составляет 1,32.
При α=0,3 табличное
значение t-критерия составляет 1,06.
Значим только Х3.
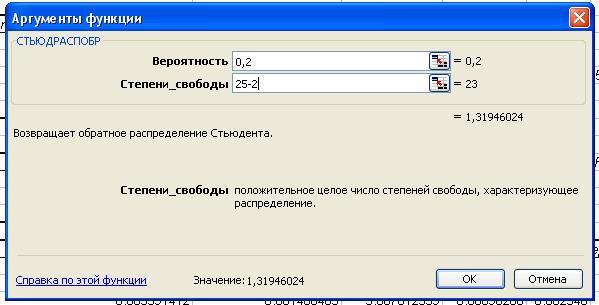
Рис.5
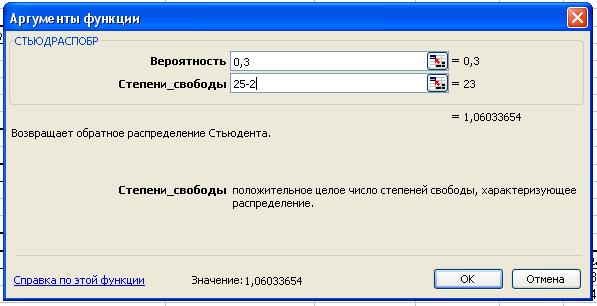
Рис.6
Проверим нулевую гипотезу о значимости
уравнения проверим с помощью F-критерия:
Значение
F-критерия Фишера можно найти в таблице 6
протокола EXCEL.
Табличное значение
F-критерия при доверительной вероятности 0,95 при 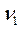 = k =4 и
= k =4 и 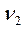 =n – k -1= 25 – 4 - 1=20 составляет 2.86. Табличное значение
F-критерия можно найти с помощью функции FРАСПОБР
=n – k -1= 25 – 4 - 1=20 составляет 2.86. Табличное значение
F-критерия можно найти с помощью функции FРАСПОБР
Поскольку F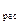 =
15,53004412>F
=
15,53004412>F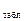 , уравнение регрессии следует признать адекватным.
, уравнение регрессии следует признать адекватным.
Оценим качество уравнения регрессии с помощью коэффициента детерминации
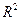
Значение коэффициентов детерминации и множественной
корреляции можно найти в таблице Регрессионная
статистика.
Коэффициент детерминации:
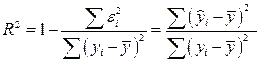 =
0,756454493
=
0,756454493
Он показывает долю
вариации результативного признака под воздействием изучаемых факторов.
Следовательно, около 75% вариации зависимой переменной учтено в модели и обусловлено
влиянием включенных факторов.
Чем ближе R2 к 1, тем выше качество
модели.
Коэффициент множественной корреляции R:
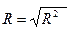 = 0,869743924.
= 0,869743924.
Он показывает тесноту
связи (связь тесная) зависимой переменной Y с включенными в модель
объясняющими факторами.
4.
Дайте сравнительную оценку силы связи факторов с
результатом с помощью коэффициентов эластичности, 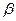 и
и 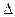 коэффициентов.
коэффициентов.
Проанализируем влияние факторов на зависимую
переменную по модели.
Учитывая, что
коэффициент регрессии невозможно использовать для непосредственной оценки
влияния факторов на зависимую переменную из-за различия единиц измерения,
используем коэффициент эластичности
(Э):
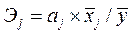
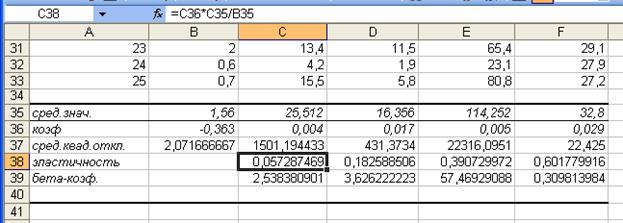
Рис.7 Лист Excel
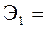 0.004´25.512/1.56=0.057
0.004´25.512/1.56=0.057
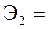 0,017´16.356/1.56=0.183
0,017´16.356/1.56=0.183
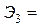 0.005´114.252/1.56=0,391
0.005´114.252/1.56=0,391
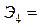 0.029´32.8/1.56=0,602
0.029´32.8/1.56=0,602
Коэффициент
эластичности показывает, на сколько процентов изменяется зависимая переменная
при изменении фактора на один процент. Видим, что при изменении фактора рыночная
капитализация на 1 процент чистый доход
измениться на 60,2%.
Рассчитаем
бета-коэффициенты:
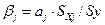
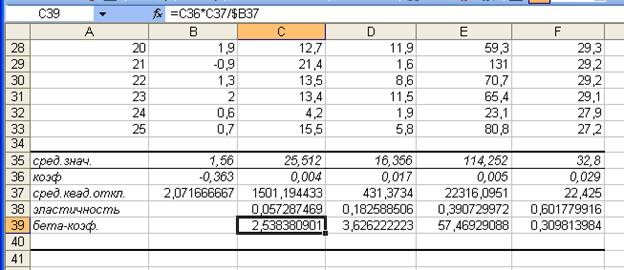
Рис.8 Расчет в Excel β
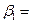 2,538
2,538
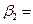 3,626
3,626
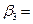 57,469
57,469
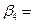 0,310
0,310
При неизменном уровне
остальных признаков увеличение оборотов капитала на величину
среднеквадратического отклонения увеличим чистый доход на на 2,538 ее
среднеквадратического отклонения.
При неизменном уровне остальных
признаков увеличение использ. капитала на величину среднеквадратического
отклонения увеличим чистый доход на 3,626 ее среднеквадратического отклонения.
При неизменном уровне
остальных признаков увеличение числен служащих на величину среднеквадратического
отклонения увеличим чистый доход на на 57,469 ее среднеквадратического
отклонения.
При неизменном уровне
остальных признаков увеличение рыночной капитализации компании на величину
среднеквадратического отклонения увеличим чистый доход на 0,310 ее среднеквадратического
отклонения.
Вычислим 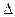 -коэффициенты:
-коэффициенты:
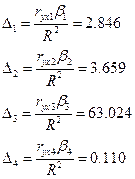
Доля влияния
оборотного капитала в суммарном
влиянии всех факторов составляет
2,846%, а доля влияния использ капитала -3,659%, числ служащих -63,024%, рыночн
капитализация компании – 0,11%.
5. Оцените точность уравнения через
среднюю относительную ошибку аппроксимации.
Определим среднюю относительную ошибку:
|
|Ei/y|
|
|
0,390359042
|
|
0,191027097
|
|
0,424732064
|
|
0,50998879
|
|
0,511391504
|
|
0,220821273
|
|
0,137215887
|
|
0,025534515
|
|
0,097717404
|
|
0,429442205
|
|
0,362788575
|
|
0,471612953
|
|
0,911705963
|
|
0,289205239
|
|
0,717182927
|
|
0,017792297
|
|
0,132805138
|
|
0,22823269
|
|
0,233230064
|
|
0,819621014
|
|
1,705917678
|
|
0,241092749
|
|
0,875329767
|
|
0,011615033
|
|
0,301640936
|
|
0,410320112
|
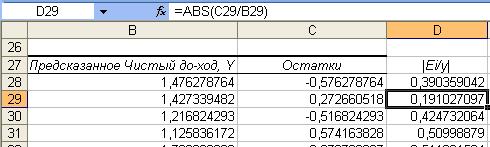
Рис.9 Рабочий лист Excel
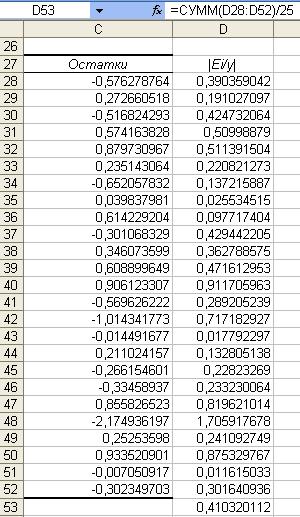
Рис.10 Расчет в Excel
Еотн =1/n*∑|
yi – ŷi / yi |*100% = 1/n∑ | εi
/ yi |*100% = 41%
Ошибка
аппроксимации меньше 7% свидетельствует о хорошем качестве модели.
В среднем расчетные значения у для линейной модели отличаются
от фактических значений на 41%
6. Отберите информативные факторы в
модель по t-критерию для коэффициентов
регрессии. Постройте модель только с
информативными факторами и оцените ее параметры.
В модель отбираем X3
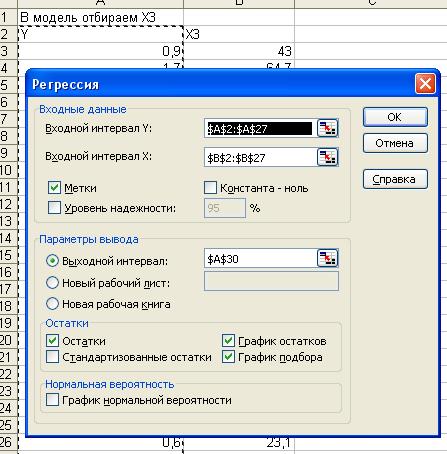
Рис.11 Диалоговое окно Регрессия
|
Регрессионная
статистика
|
|
|
|
Множественный
R
|
0,82956794
|
|
|
|
R-квадрат
|
0,688182968
|
|
|
|
Нормированный
R-квадрат
|
0,674625705
|
|
|
|
Стандартная
ошибка
|
0,821015883
|
|
|
|
Наблюдения
|
25
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
|
Регрессия
|
1
|
34,21645715
|
34,21645715
|
|
Остаток
|
23
|
15,50354285
|
0,674067081
|
|
Итого
|
24
|
49,72
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
0,646798516
|
0,208305812
|
3,105043066
|
|
X3
|
0,007992871
|
0,001121855
|
7,124689806
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
|
1
|
0,990491964
|
-0,090491964
|
|
|
2
|
1,163937262
|
0,536062738
|
|
|
3
|
0,838627417
|
-0,138627417
|
|
|
4
|
1,048040634
|
0,651959366
|
|
|
5
|
1,49404283
|
1,10595717
|
|
|
6
|
1,418909843
|
-0,118909843
|
|
|
7
|
3,420324711
|
0,679675289
|
|
|
8
|
1,330988264
|
0,269011736
|
|
|
9
|
6,601487321
|
0,298512679
|
|
|
10
|
0,679569287
|
-0,279569287
|
|
|
11
|
0,861007456
|
0,438992544
|
|
|
12
|
0,988094103
|
0,911905897
|
|
|
13
|
1,140757937
|
0,759242063
|
|
|
14
|
2,341287143
|
-0,941287143
|
|
|
15
|
1,486049959
|
-1,086049959
|
|
|
16
|
0,914559691
|
-0,114559691
|
|
|
17
|
1,781786181
|
0,018213819
|
|
|
18
|
1,414114121
|
-0,514114121
|
|
|
19
|
1,765800439
|
-0,665800439
|
|
|
20
|
1,120775759
|
0,779224241
|
|
|
21
|
1,693864601
|
-2,593864601
|
|
|
22
|
1,211894487
|
0,088105513
|
|
|
23
|
1,169532272
|
0,830467728
|
|
|
24
|
0,831433834
|
-0,231433834
|
|
|
25
|
1,292622483
|
-0,592622483
|
|
7. Рассчитайте прогнозное значение
результата, если прогнозные значения факторов составляют 80% от их максимальных
значений.
x3=596
Y= y=0,6467+0,0079*596= 5,3551
8. Рассчитайте ошибки и доверительный
интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а = 0,10).
Доверительный интервал
прогноза будет иметь следующие границы:
Верхняя граница прогноза: Yпр+U(1)
Нижняя граница прогноза Yпр- U(1)
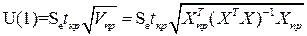
Se= 0,754
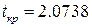
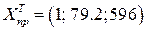
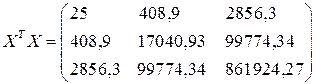
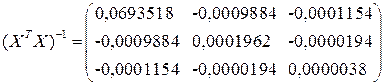
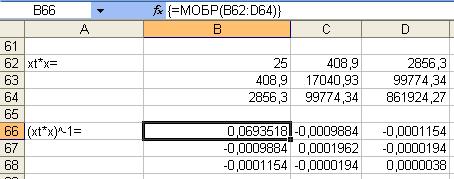
Рис.12 Лист Excel
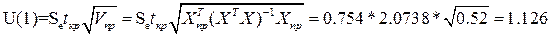
нижняя граница 5,719-1,126=4,594
верхняя граница 5,719+1,126=6,845