ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
ФИЛИАЛ
В Г.УФЕ
КАФЕДРА
МАТЕМАТИКИ И ИНФОРМАТИКИ
О Т Ч Е Т
о результатах выполнения
лабораторной работы № 2
по дисциплине
Экономико-математические
методы и прикладные модели
Вариант № _4_
Выполнил:
_3курс, ФиК, 3 группа _
Курс, поток, специальность, группа
05ФФД12454
______________________________
№
зачетной книжки
______________________________
Ф.И.О.
Проверил: Фархиева С.А.
________________________
Ф.И.О.
Уфа, 2007 г.
Задача
На основании данных, приведенных в табл. 1 требуется:
1) построить линейную модель Y(t) = aQ +axt, параметры которой оценить МНК;
2)
оценить
адекватность построенной модели на основе исследования:
·
случайности
остаточной компоненты по критерию пиков;
·
независимости
уровней ряда остатков по J-критерию (в
качестве
критических значений следует использовать уровни ,d1
=1,08 и d2, =1,36) по первому
коэффициенту автокорреляции, критический уровень которого r(1)=0,36;
·
нормальности
распределения остаточной компоненты по RS-критерию
с
критическими уровнями 2,7 - 3,7;
3) для оценки точности модели используйте
среднеквадратическое отклонение и
среднюю по модулю относительную ошибку;
4) построить
точечный и интервальный
прогнозы на два шага вперед (для
вероятности Р = 70% используйте коэффициент равный 1,12);
5) отобразить на
графике фактические данные,
результаты расчетов и
прогнозирования.
Исходные данные Таблица 1
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Y
|
30
|
28
|
33
|
37
|
40
|
42
|
44
|
49
|
47
|
Решение
1. Введем
исходные данные (Рис. 1).
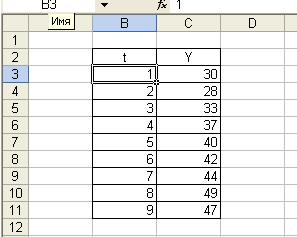
Рис. 1.
2.
Оценим параметры модели.
Оценим
параметры модели с помощью настройки EXCEL Анализ данных.
Построим
линейную однопараметрическую модель регрессии Y от t.
Для
проведения
регрессионного анализа выполним следующие действия:
- Выбираем
команду Сервис–>Анализ данных;
- В
диалоговом окне Анализ данных выбираем инструмент Регрессия (Рис. 2), затем, щелкнем
по кнопке ОК;
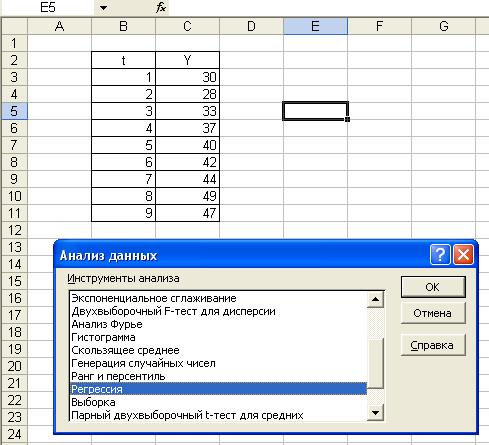
Рис. 2
·
В
диалоговом окне Регрессия в поле Входной интервал Y введем адрес диапазона ($С$2:$С$11). В
поле Выходной интервал X введем адрес
диапазона, который содержит значения независимой переменной t ($В$2:$В$11) (Рис. 3);
·
Так
как выделили заголовки столбцов, установим флажок Метки в первой строке;
·
выберем
параметры ввода. В данном случае - Новый рабочий лист;
·
в
поле График подбора поставим флажок;
- в
поле Остатки поставим флажок и нажмем кнопку ОК;
Результат регрессионного анализа показан на Рис. 4.
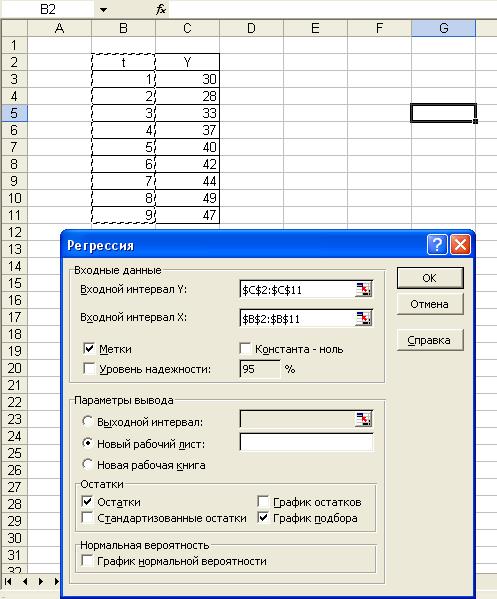
Рис. 3
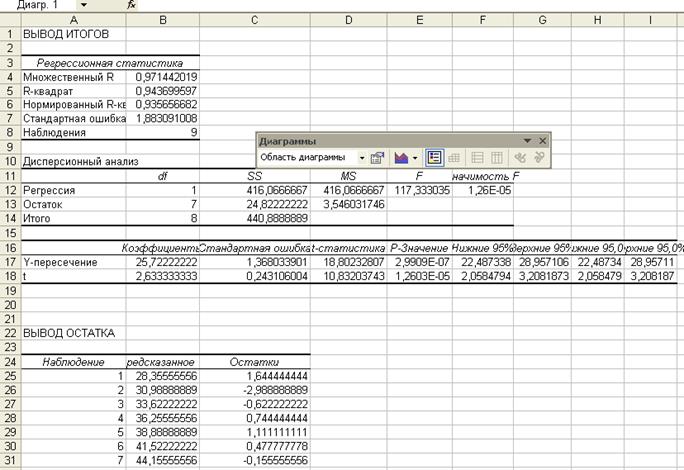
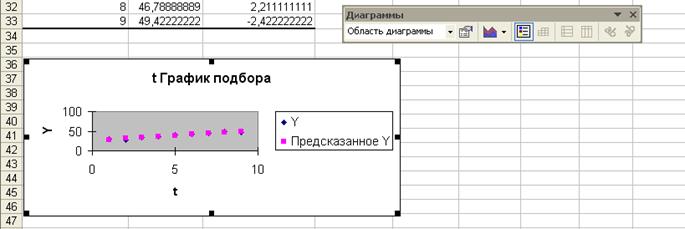
Рис. 4
В
ячейки В17 и В18 содержатся коэффициенты уравнения регрессии (а0 = 25,7, а1 =2,63)
Таким
образом, уравнение регрессии имеет вид: Y(t)=25.7+2.63t.
При
вычисление в «ручную» получаем те же
результаты.
Оценим
параметры модели «вручную».
Для
того, чтобы рассчитать коэффициенты уравнения регрессии а0, а1, проведем промежуточные расчеты Excel (рис. 5)
|
|
|
|
|
|
|
|
t
|
Y
|
t-tcp
|
(t-tcp)^2
|
y-ycp
|
(t-tcp)*(y-ycp)
|
|
1
|
30
|
-4
|
16
|
-8,888888889
|
35,55555556
|
|
2
|
28
|
-3
|
9
|
-10,88888889
|
32,66666667
|
|
3
|
33
|
-2
|
4
|
-5,888888889
|
11,77777778
|
|
4
|
37
|
-1
|
1
|
-1,888888889
|
1,888888889
|
|
5
|
40
|
0
|
0
|
1,111111111
|
0
|
|
6
|
42
|
1
|
1
|
3,111111111
|
3,111111111
|
|
7
|
44
|
2
|
4
|
5,111111111
|
10,22222222
|
|
8
|
49
|
3
|
9
|
10,11111111
|
30,33333333
|
|
9
|
47
|
4
|
16
|
8,111111111
|
32,44444444
|
|
45
|
350
|
|
60
|
2,84217E-14
|
158
|
|
5
|
38,88889
|
|
|
|
|
Рис. 5
Параметры
линейной модели найдем по формулам:
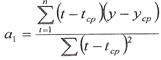
=158/60=2,63
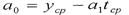=38,89-13,17≈25,7
3. Оценим
качество построенной модели.
Для этого исследуем адекватность модели.
Модель является адекватной, если математические ожидаем значений остаточного
ряда близко или равно нулю и если значения остаточного ряда случайны,
независимы и подчинены нормальному закону распределения.
·
При
проверке независимости определяется отсутствием в ряду остатков систематической
составляющей, например, с помощью d-критерия Дарбина-Уотсона
по формуле:
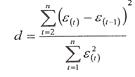
Проведем
промежуточные расчеты в Excel (рис.6)
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
(e(t)-e(t-1)^2
|
e(t)^2
|
|
|
|
1
|
28,35555556
|
1,644444444
|
|
2,70419753
|
|
|
|
2
|
30,98888889
|
-2,988888889
|
21,46777778
|
8,93345679
|
|
|
|
3
|
33,62222222
|
-0,622222222
|
5,601111111
|
0,38716049
|
|
|
|
4
|
36,25555556
|
0,744444444
|
1,867777778
|
0,55419753
|
|
|
|
5
|
38,88888889
|
1,111111111
|
0,134444444
|
1,2345679
|
|
|
|
6
|
41,52222222
|
0,477777778
|
0,401111111
|
0,2282716
|
|
|
|
7
|
44,15555556
|
-0,155555556
|
0,401111111
|
0,02419753
|
|
|
|
8
|
46,78888889
|
2,211111111
|
5,601111111
|
4,88901235
|
|
|
|
9
|
49,42222222
|
-2,422222222
|
21,46777778
|
5,86716049
|
|
|
|
|
|
|
56,94222222
|
24,8222222
|
|
|
|
|
|
|
|
|
|
Рис. 6.
Тогда,
d=56,94/24,82= 2,29
d’=4-d. Таким образом,
d’=4-2,29=1.71
Так как d’>d2 , то по данному критерию свойство независимости выполнено. Модель по этому критерию адекватна.
·
Проверку
случайностей уровней ряда остатков проведем на основе критерия поворотных точек.
Значение случайности переменной считается поворотной точкой, если оно
одновременно больше (меньше) соседних с ним элементов.
Критерий случайности отклонений от
тренда при уровни вероятности 0.95 можно представить как :
p>[2/3(n-2)-1.96√16n-29/90],
где p-фактическое
количество поворотных точек случайном ряду ;
1.96-квантиль нормального распределения
для 5%-ного уровня значимости. Квадратные скобки означают, что от результата
вычисления следует взять целую часть. Так как p=
6 ,значит, неравенство выполняется (6>3). Следовательно, свойство случайности выполняется. Модель по
этому критерию адекватна.
·
Соответствие
ряда остатков нормальному закону распределения определим при помощи RS-критерия:
,
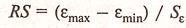где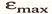 
- максимальный уровень ряда остатков, 
=2,21;
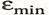- минимальный уровень ряда остатков,
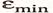=-2,99;
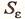- среднеквадратическое отклонение,
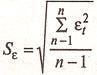
=3,1, тогда RS=[2.21-(-2.99)]/3.1=1.9
Расчетное значение не попадает в интервал (2,7-3,7), следовательно, свойство
нормальности распределения не выполняется.
·
Проверка
равенства нулю математического ожидания
уровней ряда остатков.
В нашем случае е =0,
поэтому гипотеза о равенстве математического ожидения значений остаточного ряда
нулю выполняется
Вывод: данная модель статистически не
адекватна.
4. Построим точечный и интервальные
прогнозы на два шага вперед (для вероятности 70% использовать t=1,12):
Y10=a0+a1t=25.7+2.63*10≈52
Y11=a0+a1t=25.7+2.63*11≈54.63
Для построения интервального прогноза
рассчитаем доверительный интервал. Примем значения доверительная вероятность
равна 70%, а критерий Стьюдента равен 1,12. ширину доверительного интервала
вычислим по формуле:
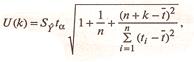
где
-
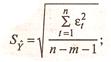
стандартная ошибка (среднеквадратическое отклонение от модели);
m – количество факторов в модели, для
линейной модели m=1.
Находим из таблицы рис.5, следующие
значения:U(1)=2,63, U(2)=2,78
Далее вычисляем верхнюю и нижнюю границы
прогноза (рис. 7.).
|
n+k
|
U(k)
|
Прогноз
|
Формула
|
Верхняя граница
|
нижняя граница
|
|
10
|
U(1)=2,63
|
52
|
Прогноз+U(1)
|
54,63
|
49,37
|
|
11
|
U(2)=2,78
|
54,63
|
Прогноз-U(2)
|
57,41
|
51,85
|
Рис. 7
5. Отобразим на графике фактические данные, результаты
расчетов и прогнозирования.
Для этого преобразуем график подбора,
который был получен с помощью инструмента Регрессия (рис. 4).
·
Выберем
тип диаграммы – точечная, на которой значения соединены отрезками (рис. 8).
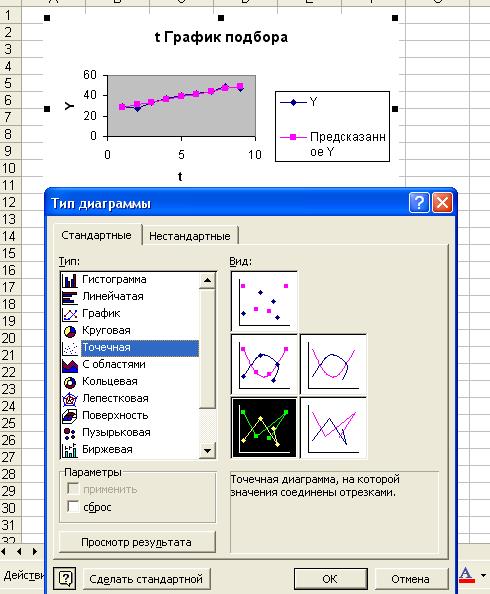
Рис. 8
·
Укажем
в формате области построения тип заливки – обычная; рамка – невидимая.
·
Далее
на графике изобразим результаты прогнозирования.
·
Для
этого «кликнем» правой кнопкой мышки и в появившемся меню выберем Исходные
данные. Затем последовательно нажимаем кнопки Ряд, Добавить и указать диапазоны
размещения данных (рис.9). в диалоговом окне Исходные данные в поле Y введем адрес
диапазона ячеек, который представляет прогноз зависимой переменной. В поле
значения Х введем адрес диапазона, который содержит значения
независимой переменной t.
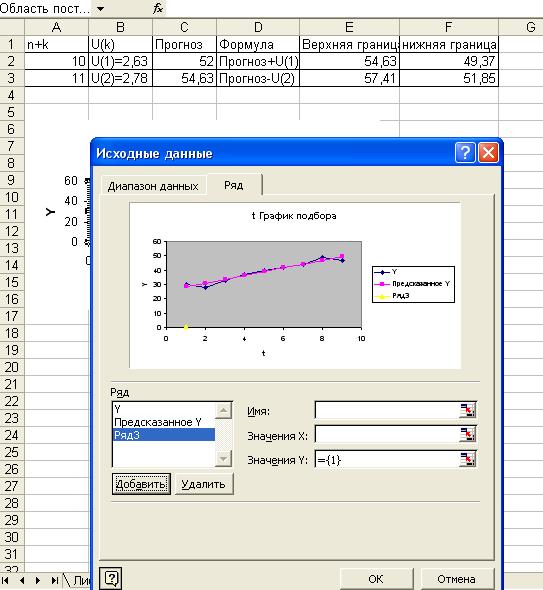
Рис. 9
·
Аналогично
вводятся данные для верхних и нижних границ прогнозы (рис. 10, 11).
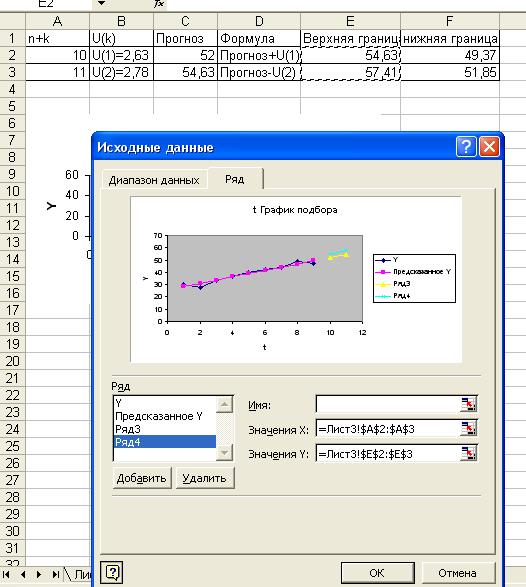
Рис.10
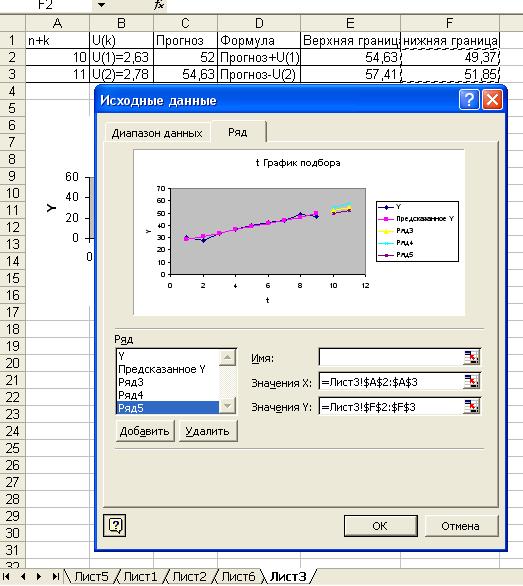
Рис. 11
Прогноз модели Y(t)=25.7+2.63t.
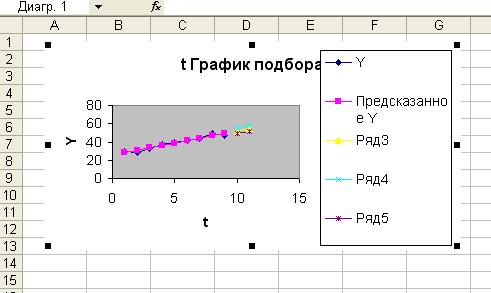
Рис. 12 результаты
моделирования и прогнозирования
Мастер диаграмм
Имеем
временной ряд вида:
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Y
|
30
|
28
|
33
|
37
|
40
|
42
|
44
|
49
|
47
|
Необходимо
построить наиболее точную модель,
используя функцию «Мастер диаграмм» системы Excel.
1. Активизируем
окно «Мастер диаграмм», выберем Тип
диаграмм «График с маркерами, помечающими точки данных» (рис. 1).
Рис.
1
2. Выбрав вставку
«Ряд», нажмем кнопку «Добавить» (рис .2).
Рис.
2
3. В окне «Имя»
напишем «фактический ряд». В окне «Значение» введем адрес ячеек, где заключен
фактический ряд. В окне «Оси Х» введем адрес ячеек, где заключен временной ряд
(рис.3).
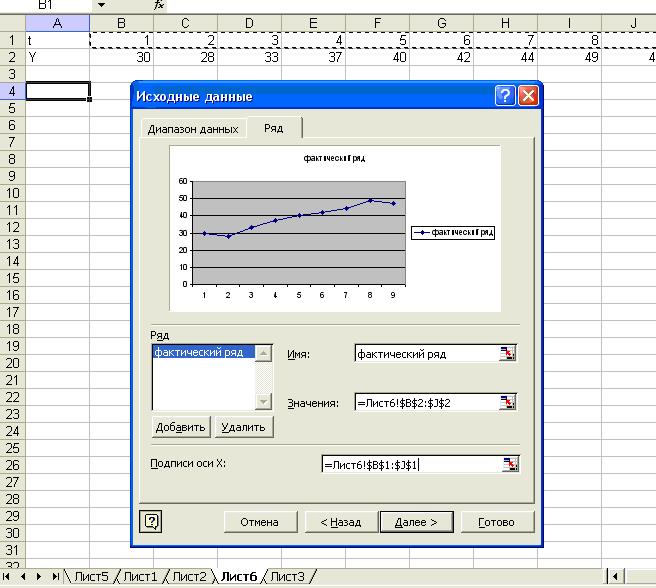
Рис.3
4. Щелкнув кнопку
«Готово», получим следующую диаграмму (рис. 4).
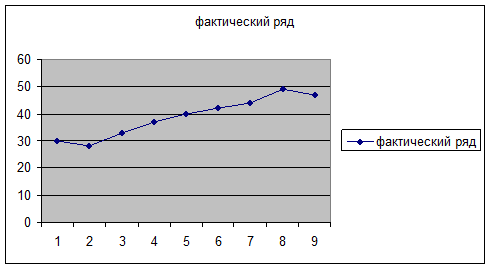
Рис.4
5. Щелкнув правой
кнопкой мыши, получим следующее окно , где выберем «Добавить линию тренда» (рис.
5).
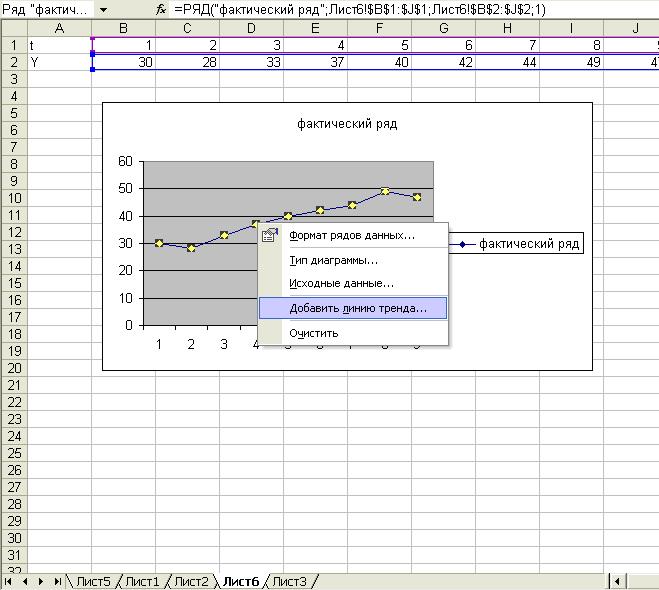
Рис.
5
6. Появится окно
«Линию тренда», где представлены 6 типов линий (рис.6).
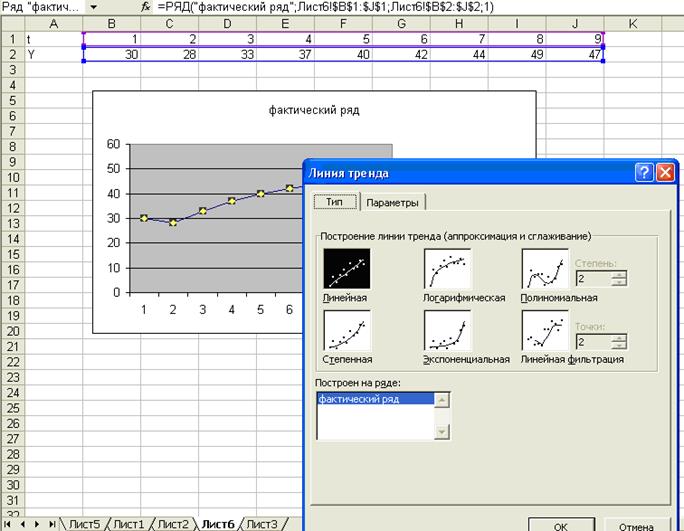
Рис.
6
7. Для выбора
лучшей линии тренда используем их поочередно и во вкладыше «Параметры» выберем
функцию «показать уравнение не диаграмме» и «поместить на диаграмму величину
достоверности аппроксимации» (рис. 7).
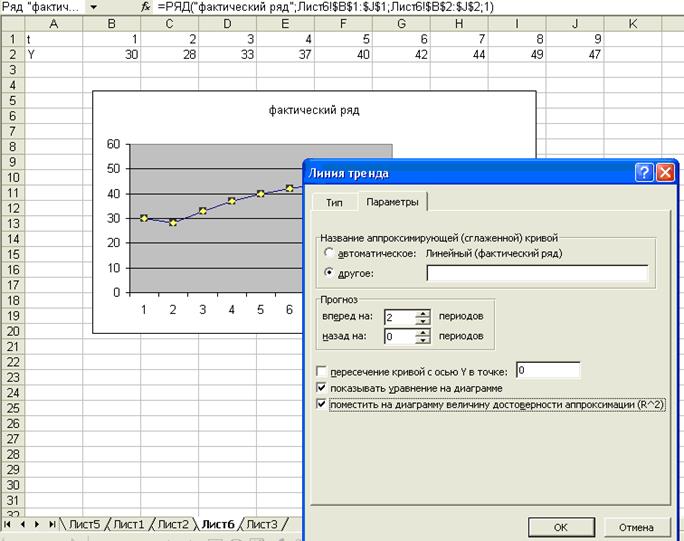
Рис.
7
8. Таким образом,
получаем несколько моделей и их значения R^2.
Тогда лучшей моделью является полиномиальная модель, т.к R^2 полиномиальной модели оказался максимальным, т.е.
ближе к 1 (R^2
= 0,9471) (рис.8).
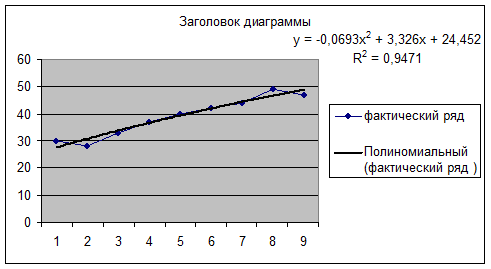
Рис.
8
Отчет по статэксперту
1.
Создать файл исходных данных по своему варианту в среде Microsoft Excel.
Для
этого инсталировать (запустить) программу Microsoft Excel-2000.
Ввести
данные (шаблон). Для этого в ячейке А1 записать «Недели»; в ячейке А2 «Спрос» и
далее числовые данные о времени и уровнях моделируемого показателя.
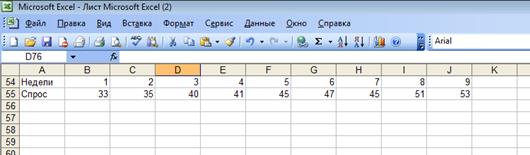
Сохранить
таблицу данных в формате Microsoft Excel.
Свернуть
окно Excel . Перенести файл исходных данных в среду Microsoft Word-2000.
2.
Инсталяция программы «СтатЭксперт».
Выполнить
последовательно действия: «ПУСК» - «ПРОГРАММЫ» (в главном меню) – «Olymp» - «СтатЭксперт» - «Не отключать
макросы». На экране появиться картинка «СтатЭксперт».
Дать
команду «Начало работы» - «OK». Появиться таблица программы «СтатЭксперт».
3.
Включить режимы обработки программы.
Активизировать файл исходных данных, выполнив последовательно
действия: «ФАЙЛ» - выбор имени файла из всплывающего меню в формате Excel.
Отметить цифровые данные таблицы.
Вызвать меню «СтатЭкс» (вторая строка панели
инструментов), указать «ВРЕНМЕННЫЕ РЯДЫ» (появиться окно «Установка блока
данных»).
4.
Предварительная обработка данных.
Ориентация таблицы: флажок в окно «по строкам», либо «по
колонкам» (в зависимости от ориентации шаблона).
Наличие
наименований: убрать все флажки в окнах.
Команда
«Установить» (появиться окно «Обработка временных рядов»).
Окно
«Обработка временных рядов».
Этапы
обработки: флажок в окно «Предварительный анализ».
Выделяем
щелчком левой кнопки мышки «Показатель 2».
Команда
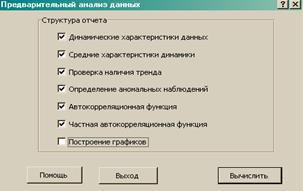
«Вычислить» (появиться окно «Предварительный анализ данных»).
Окно
«Предварительный анализ данных» .
Оставить
все флажки, кроме «Построение графиков».
Команда
«Вычислить».
При
обнаружении аномальных данных в моделируемом временном ряду нажать клавишу «Да»
и выполнить рекомендации всплывающего сообщения.
5.
Полученный протокол отчета перенести в файл, сформированный в
среде Microsoft Word. Для этого:
·
Отметить
копируемый отчет.
·
Скопировать
в буфер файл в формате Excel.
·
Свернуть
окно отчета.
·
Открыть
среду Microsoft Word.
·
Сохранить
протокол отчета в среде Word (для создания будущего отчета по лабораторной работе)
(см. табл.1).
Таблица 1.
Отчет по предварительной обработке данных.
|
Cтатистики временного ряда - Показатель- 2
|
|
|
|
|
|
|
|
|
|
|
|
Базисные
характеристики
|
|
|
|
|
|
Наблюдение
|
Абс.
прирост
|
Темп
роста
|
Темп
прироста
|
|
|
2
|
2,000
|
106,061
|
6,061
|
|
|
3
|
7,000
|
121,212
|
21,212
|
|
|
4
|
8,000
|
124,242
|
24,242
|
|
|
5
|
12,000
|
136,364
|
36,364
|
|
|
6
|
14,000
|
142,424
|
42,424
|
|
|
7
|
12,000
|
136,364
|
36,364
|
|
|
8
|
18,000
|
154,545
|
54,545
|
|
|
9
|
20,000
|
160,606
|
60,606
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цепные
характеристики
|
|
|
|
|
|
Наблюдение
|
Абс.
прирост
|
Темп
роста
|
Темп
прироста
|
|
|
2
|
2,000
|
106,061
|
6,061
|
|
|
3
|
5,000
|
114,286
|
14,286
|
|
|
4
|
1,000
|
102,500
|
2,500
|
|
|
5
|
4,000
|
109,756
|
9,756
|
|
|
6
|
2,000
|
104,444
|
4,444
|
|
|
7
|
-2,000
|
95,745
|
-4,255
|
|
|
8
|
6,000
|
113,333
|
13,333
|
|
|
9
|
2,000
|
103,922
|
3,922
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Средние
характеристики
|
|
|
|
|
|
Характеристика
|
Значение
|
|
|
|
|
Среднее
арифметическое
|
43,333
|
|
|
|
|
Средний
темп роста (%)
|
106,101
|
|
|
|
|
Средний
темп прироста (%)
|
6,101
|
|
|
|
|
Средний
абсолютный прирост
|
2,500
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гипотеза
об отсутствии тренда
|
|
|
|
|
|
Метод
проверки
|
Результат
|
|
|
|
|
Метод
Форстера-Стюарта
|
Нет
|
|
|
|
|
Метод
сравнения средних
|
Нет
|
|
|
|
|
Вывод:
гипотеза отвергается
|
|
|
|
|
|
|
|
|
|
|
|
Проверка
однородности данных
|
|
|
|
|
|
Аномальные
наблюдения не обнаружены
|
|
|
|
|
|
|
|
|
|
|
|
Автокорреляционная
функция
|
|
|
|
|
|
Лаг
|
Исходный
ряд
|
Разностный
ряд (d=1)
|
|
|
|
1
|
0,596
|
-0,528
|
|
|
|
2
|
0,238
|
-0,023
|
|
|
|
Cтандартные
отклонения = +0.4502, +0.4163
|
|
|
|
|
|
|
|
|
|
|
|
Частная
автокорреляционная функция
|
|
|
|
|
|
Лаг
|
Исходный
ряд
|
Разностный
ряд (d=1)
|
|
|
|
1
|
0,704
|
-0,750
|
|
|
|
2
|
-0,181
|
-0,419
|
|
|
|
Cтандартные
отклонения = +0.3333, +0.3780
|
|
|
|
|
6.
Построение модели и прогнозирование.
Включить
режимы обработки программы: активизировать файл исходных данных (шаблон) в
формате Excel, отметить цифровые данные таблицы.
Вызвать меню «СтатЭкс» (верхняя строчка), указать
«ВРЕНМЕННЫЕ РЯДЫ» (появиться окно «Установка блока данных»).
Предварительная обработка данных: ориентация таблицы (в
зависимости от ориентации шаблона), наличие наименований (убрать все флажки в
окнах); команда «Установить» (появиться окно «Обработка временных рядов»).
Этапы
обработки: флажок в окно «Построение моделей и прогнозирование»; выделяем щелчком
левой кнопки мышки «Показатель 2»; команда «Вычислить» (появиться окно
«Построение моделей и прогнозирование»).
Окно
«Построение моделей и прогнозирование» .
Класс
моделей: «Кривые роста».
Тип
прогноза: «Прогноз вперед».
Способ
построения прогноза: «На основе одной лучшей модели».
Структура
отчета: все флажки кроме «Статистика ретропрогноза».
Период
прогноза: в соответствии с условием задачи.
Вероятность
свершения прогноза: в соответствии с условием задачи.
«Вычислить».
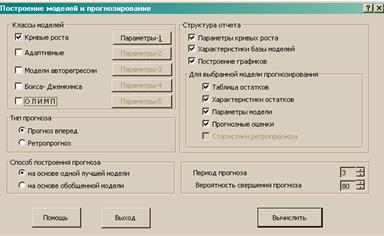
Окно «Построение моделей и прогнозирование».
7.
Формирование отчета по графикам.
Сохранить
протокол отчета в среде Word (для создания будущего отчета по лабораторной работе)
(см. табл.2).
Таблица 2. Отчет по построению модели
и прогнозирование.
|
Модели временного ряда - Показатель- 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
кривых роста
|
|
|
|
|
|
|
Функция
|
Критерий
|
Эластич
ность
|
|
|
|
|
Y(t)=+31.333+2.400*t
|
2,629
|
0,277
|
|
|
|
|
Y(t)=+30.024+3.114*t
-0.071*t*t
|
2,805
|
0,274
|
|
|
|
|
Y(t)=
+32.288*exp(+0.057*t)
|
3,265
|
0,283
|
|
|
|
|
Y(t)=
+30.615+8.941*ln(t)
|
4,734
|
0,199
|
|
|
|
|
Y(t)=
(+30.302)*(+1.096)**t*(+0.997)**(t*t)
|
2,959
|
0,283
|
|
|
|
|
Y(t)=
+26.239+1.082*t+5.448*sqr(t)
|
2,706
|
0,262
|
|
|
|
|
Y(t)=
t/(+0.022+0.017*t)
|
12,331
|
0,198
|
|
|
|
|
Выбрана
функция Y(t)=+31.333+2.400*t
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристики
базы моделей
|
|
|
|
|
|
|
Модель
|
Адекват
ность
|
Точность
|
Качество
|
|
|
|
Y(t)=+31.333+2.400*t
|
80,984
|
78,574
|
79,176
|
|
|
|
Лучшая
модель Y(t)=+31.333+2.400*t
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметры
моделей
|
|
|
|
|
|
|
Модель
|
a1
|
a2
|
|
|
|
|
Y(t)=+31.333+2.400*t
|
31,333
|
2,400
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
остатков
|
|
|
|
|
|
|
номер
|
Факт
|
Расчет
|
Ошибка
абс.
|
Ошибка
относит.
|
|
|
1
|
33,000
|
33,733
|
-0,733
|
-2,222
|
|
|
2
|
35,000
|
36,133
|
-1,133
|
-3,238
|
|
|
3
|
40,000
|
38,533
|
1,467
|
3,667
|
|
|
4
|
41,000
|
40,933
|
0,067
|
0,163
|
|
|
5
|
45,000
|
43,333
|
1,667
|
3,704
|
|
|
6
|
47,000
|
45,733
|
1,267
|
2,695
|
|
|
7
|
45,000
|
48,133
|
-3,133
|
-6,963
|
|
|
8
|
51,000
|
50,533
|
0,467
|
0,915
|
|
|
9
|
53,000
|
52,933
|
0,067
|
0,126
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристики
остатков
|
|
|
|
|
|
|
Характеристика
|
Значение
|
|
|
|
|
|
Среднее
значение
|
0,000
|
|
|
|
|
|
Дисперсия
|
2,044
|
|
|
|
|
|
Приведенная
дисперсия
|
2,629
|
|
|
|
|
|
Средний
модуль остатков
|
1,111
|
|
|
|
|
|
Относительная
ошибка
|
2,632
|
|
|
|
|
|
Критерий
Дарбина-Уотсона
|
2,396
|
|
|
|
|
|
Коэффициент
детерминации
|
0,999
|
|
|
|
|
|
F
- значение ( n1 = 1, n2 = 7)
|
6560,826
|
|
|
|
|
|
Критерий
адекватности
|
80,984
|
|
|
|
|
|
Критерий
точности
|
78,574
|
|
|
|
|
|
Критерий
качества
|
79,176
|
|
|
|
|
|
Уравнение
значимо с вероятностью 0.95
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
прогнозов (p =70%)
|
|
|
|
|
|
|
Упреждение
|
Прогноз
|
Нижняя
граница
|
Верхняя
граница
|
|
|
|
1
|
55,333
|
53,663
|
57,003
|
|
|
|
2
|
57,733
|
55,795
|
59,672
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В
активном окне протокола «Стат Эксперт»
нажать ярлык диаграммы (слева от окна, второй ярлык сверху). В появившимся меню
выбрать «Аппроксимация и прогноз» (появиться график).
Окно «Графики отчета».
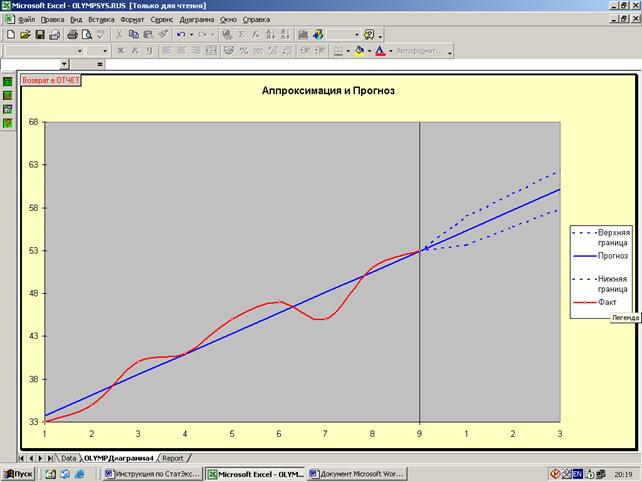
Рис.
8. График «Аппроксимация и прогноз».