`По предприятиям лёгкой
промышленности региона получена информация, характеризующая зависимость объема
выпуска продукции (Y, млн. руб.) от объёма капиталовложений (X, млн. руб.).
Вариант 1
|
|
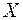
66
|
58
|
73
|
82
|
81
|
84
|
55
|
67
|
81
|
59
|
|
|
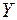
133
|
107
|
145
|
162
|
163
|
170
|
104
|
132
|
159
|
116
|
Требуется:
1. найти параметры уравнения линейной
регрессии, дать экономическую интерпретацию коэффициента регрессии.
2. вычислить остатки; найти остаточную
сумму квадратов; оценить дисперсию остатков S2; построить график остатков.
3. проверит выполнение предпосылок МНК.
4. осуществить проверку значимости
параметров уравнения регрессии с помощью t-критерию Стьюдента (α=0,05).
5. вычислить коэффициент детерминации,
проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05),
найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве
модели.
6. Осуществить прогнозирование среднего
значения показателя 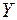при уровне
значимости 
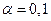, если прогнозное значения фактора Х составит
80% от его максимального значения.
7. Представить графически: фактические и
модельные значения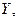 
точки прогноза.
8. Составить уравнения нелинейной
регрессии:
·
гиперболической;
·
степенной;
·
показательной.
Привести графики построенных
уравнений регрессии.
9. Для указанных моделей найти
коэффициенты детерминации, коэффициенты эластичности и средние относительные
ошибки аппроксимации. Сравнить модели
по этим характеристикам и сделать вывод.
Решение:
1.Для вычисления параметров модели промежуточные расчеты
приведём в виде таблицы (таблица выполнена с помощью средств Excel):
табл.1.1
|
Наблюд
ение
|
x
|
y
|
y-yср
|
x-xср
|
(x-xср)^2
|
(y-yср)(x-xср)
|
yx
|
X^2
|
(y-yср)^2
|
|
1,00
|
66,00
|
133,00
|
-6,10
|
-4,60
|
21,16
|
28,06
|
8778,00
|
4356,00
|
37,21
|
|
2,00
|
58,00
|
107,00
|
-32,10
|
-12,60
|
158,76
|
404,46
|
6206,00
|
3364,00
|
1030,41
|
|
3,00
|
73,00
|
145,00
|
5,90
|
2,40
|
5,76
|
14,16
|
10585,00
|
5329,00
|
34,81
|
|
4,00
|
82,00
|
162,00
|
22,90
|
11,40
|
129,96
|
261,06
|
13284,00
|
6724,00
|
524,41
|
|
5,00
|
81,00
|
163,00
|
23,90
|
10,40
|
108,16
|
248,56
|
13203,00
|
6561,00
|
571,21
|
|
6,00
|
84,00
|
170,00
|
30,90
|
13,40
|
179,56
|
414,06
|
14280,00
|
7056,00
|
954,81
|
|
7,00
|
55,00
|
104,00
|
-35,10
|
-15,60
|
243,36
|
547,56
|
5720,00
|
3025,00
|
1232,01
|
|
8,00
|
67,00
|
132,00
|
-7,10
|
-3,60
|
12,96
|
25,56
|
8844,00
|
4489,00
|
50,41
|
|
9,00
|
81,00
|
159,00
|
19,90
|
10,40
|
108,16
|
206,96
|
12879,00
|
6561,00
|
396,01
|
|
10,00
|
59,00
|
116,00
|
-23,10
|
-11,60
|
134,56
|
267,96
|
6844,00
|
3481,00
|
533,61
|
|
сумма
|
706,00
|
1391,00
|
0,00
|
0,00
|
1102,40
|
2418,40
|
100623,00
|
50946,00
|
5364,90
|
|
среднее
|
70,60
|
139,10
|
|
|
|
|
10062,30
|
5094,60
|
|
Определим линейный коэффициент парной
корреляции по следующей формуле:
ry,x=﴾∑(y-yср)*(x-xср)﴿/√∑(y-yср)2*(x-xср)2=0,994
можно сказать, что связь между
объёмом капиталовложений и объёмом выпуска продукции прямая, достаточно
сильная.
Уравнение линейной регрессии имеет
вид: y=a+b*x.
Значения параметров a и b линейной модели определим, используя
данные таблицы 1.1:
b=y*x – y*x / x2 – x 2
= 10062,30 – 70,60*139,10 /
5094,60 – 70,602 = 241,84/110,24 = 2,19
a=y-b*x=139,10-2,19*70,60=-15,514
Уравнение линейной регрессии имеет
вид:
Y=-15.514+2.19*X
С увеличением объёма капиталовложений на 1 млн. руб. объем
выпускаемой продукции увеличится в среднем на 2млн. 190 тыс.руб. Это
свидетельствует об эффективной работе предприятия.
2. Вычислим
остатки и остаточную сумму квадрвтов с помощью Excel и занесем результаты вычислений в таблицу 2.1:
Табл. 2.1
|
Набл
юд
ение
|
x
|
y
|
y-yср
|
x-xср
|
(x-xср)^2
|
(y-yср)(x-xср)
|
yx
|
X^2
|
(y-yср)^2
|
y'
|
e
|
e^2
|
|
1,00
|
66,00
|
133,00
|
-6,10
|
-4,60
|
21,16
|
28,06
|
8778,00
|
4356,00
|
37,21
|
129,026
|
3,97
|
15,79
|
|
2,00
|
58,00
|
107,00
|
-32,10
|
-12,60
|
158,76
|
404,46
|
6206,00
|
3364,00
|
1030,41
|
111,506
|
-4,51
|
20,30
|
|
3,00
|
73,00
|
145,00
|
5,90
|
2,40
|
5,76
|
14,16
|
10585,00
|
5329,00
|
34,81
|
144,356
|
0,64
|
0,41
|
|
4,00
|
82,00
|
162,00
|
22,90
|
11,40
|
129,96
|
261,06
|
13284,00
|
6724,00
|
524,41
|
164,066
|
-2,07
|
4,27
|
|
5,00
|
81,00
|
163,00
|
23,90
|
10,40
|
108,16
|
248,56
|
13203,00
|
6561,00
|
571,21
|
161,876
|
1,12
|
1,26
|
|
6,00
|
84,00
|
170,00
|
30,90
|
13,40
|
179,56
|
414,06
|
14280,00
|
7056,00
|
954,81
|
168,446
|
1,55
|
2,41
|
|
7,00
|
55,00
|
104,00
|
-35,10
|
-15,60
|
243,36
|
547,56
|
5720,00
|
3025,00
|
1232,01
|
104,936
|
-0,94
|
0,88
|
|
8,00
|
67,00
|
132,00
|
-7,10
|
-3,60
|
12,96
|
25,56
|
8844,00
|
4489,00
|
50,41
|
131,216
|
0,78
|
0,61
|
|
9,00
|
81,00
|
159,00
|
19,90
|
10,40
|
108,16
|
206,96
|
12879,00
|
6561,00
|
396,01
|
161,876
|
-2,88
|
8,27
|
|
10,00
|
59,00
|
116,00
|
-23,10
|
-11,60
|
134,56
|
267,96
|
6844,00
|
3481,00
|
533,61
|
113,696
|
2,30
|
5,31
|
|
сумма
|
706,00
|
1391,00
|
0,00
|
0,00
|
1102,40
|
2418,40
|
100623,00
|
50946,00
|
5364,90
|
1391,00
|
0,00
|
59,53
|
|
Сред
нее
|
70,60
|
139,10
|
|
|
|
|
10062,30
|
5094,60
|
|
|
|
|
Дисперсия остатков будет равна:
S2 = (∑ε2) / n-2 = 59,53/8 = 7,44
График остатков имеет вид:
Рис.1
3.Основные предпосылки
МНК:
Первое условие: т.к. ∑ε=
0, то M(ε)=0,т.е. математическое ожидание
случайной составляющей в любом наблюдении равно 0.
Второе условие: в найденной модели Y=-15.514+2.19*X возмущение ε
есть величина случайная, а объясняющая переменная x- величина неслучайная. Т.к. на
графике (рис.1) нет направленности в расположении точек ε,
то ε - случайные величины, и применение МНК
оправдано.
Третье условие: d=∑( εi- εi-1)2 / ∑ εi 2, d≈2, значит, автокорреляция
отсутствует.
Четвёртое условие: т.к. дисперсия случайной величины
постоянна для всех наблюдений, то соблюдается условие гомоскедастичность.
4. Коэффициент
Стьюдента tα для m=8 степеней свободы уровня значимости
α=0,05 равен 2,3060.
Sα=√(S2 * ∑x2 )/ n*(∑x-xср)2 = 5,86
Sβ=√ S2 / (∑x-xср)2 = 0,082
tα=|a| / Sα= 15,514/5,86=2,647
tβ=|b| / Sβ= 2,19/0,082=26,707, т.к. tβ>tтабл., tα>tтабл., то оба коэффициента считаются значимыми.
5. Коэффициент детерминации равен: R2=1-(∑ε2) / ∑(y-yср)2=1-0,011=0,9889.
Проведём оценку значимости уравнения
регрессии с помощью F-критерия Фишера:
F=(R2/1-R)*(n-2)=(0,9889/0,011)*8=719,2
F>Fтабл.=5,32 ,для α=0,05;
k1=m=1; k2=n-m-1=8.
Уравнение регрессии с вероятностью
0,95 в целом статистически значимое, т.к. F>Fтабл.
Определим среднюю относительную
ошибку:
Eотн.=1/n*∑|(y-yср)/y)|*100%=15,7%.
В среднем расчетные значения Y для линейной модели отличаются от
фактических значений на 15,7%.
6. yпрогн.=a+b*xпрогн.
X=80%x=0,8*84=67,2
yпрогн=-15,514+2,19*67,2=131,654
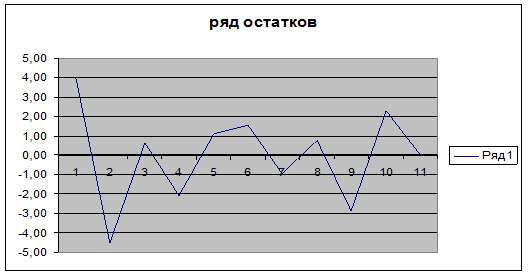
7. Фактические и модельные значения Y, точки прогноза.
Рис.2
8. Гиперболическая модель
Уравнение гиперболической функции: y’=a+b/x.
Произведём линеаризацию модели путем замены X=1/x. В результате получим линейное
уравнение: y’=a+b*X.
Рассчитаем его параметры по
данным таблицы 3.1:
Табл.3.1
|
наблюдение
|
x
|
y
|
X
|
y*X
|
X^2
|
y-ycp
|
(y-ycp)^2
|
|
1
|
66
|
133,00
|
0,015151515
|
2,015152
|
0,000229568
|
-6,10
|
37,21
|
|
2
|
58
|
107,00
|
0,017241379
|
1,844828
|
0,000297265
|
-32,10
|
1030,41
|
|
3
|
73
|
145,00
|
0,01369863
|
1,986301
|
0,000187652
|
5,90
|
34,81
|
|
4
|
82
|
162,00
|
0,012195122
|
1,97561
|
0,000148721
|
22,90
|
524,41
|
|
5
|
81
|
163,00
|
0,012345679
|
2,012346
|
0,000152416
|
23,90
|
571,21
|
|
6
|
84
|
170,00
|
0,011904762
|
2,02381
|
0,000141723
|
30,90
|
954,81
|
|
7
|
55
|
104,00
|
0,018181818
|
1,890909
|
0,000330579
|
-35,10
|
1232,01
|
|
8
|
67
|
132,00
|
0,014925373
|
1,970149
|
0,000222767
|
-7,10
|
50,41
|
|
9
|
81
|
159,00
|
0,012345679
|
1,962963
|
0,000152416
|
19,90
|
396,01
|
|
10
|
59
|
116,00
|
0,016949153
|
1,966102
|
0,000287274
|
-23,10
|
533,61
|
|
сумма
|
706
|
1391,00
|
0,14493911
|
19,64817
|
0,002150381
|
0,00
|
5364,90
|
|
среднее
|
70,6
|
139,10
|
0,014493911
|
1,964817
|
0,000215038
|
|
536,49
|
b=[y*X-y*X]/[X^2-X^2]=[1.964817-139.10*0.014493911]/[0.000215038-0.014493911*0.014493911]=-10330.45951
a=y-b*X=139.10+10330.45951*0.0144933911=288.8287607.
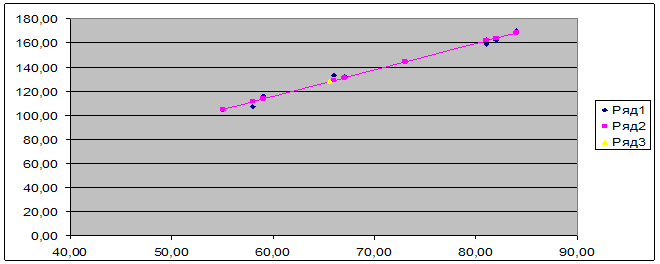
Получим следующее уравнение гиперболической модели:
y’=288.829-10330.4595/x, и её график:
Рис.3
Степенная модель
Уравнение степенной модели имеет вид:
Y=a*xb ; для построения этой модели
произведём линеаризацию переменных: lgy=lga+b*lgx. Построим
таблицу с помощью Excel:
Табл. 3.2
|
наблюдение
|
x
|
lg(x)
|
y
|
lg(y)
|
|
1,00
|
66,00
|
1,82
|
133,00
|
2,12
|
|
2,00
|
58,00
|
1,76
|
107,00
|
2,03
|
|
3,00
|
73,00
|
1,86
|
145,00
|
2,16
|
|
4,00
|
82,00
|
1,91
|
162,00
|
2,21
|
|
5,00
|
81,00
|
1,91
|
163,00
|
2,21
|
|
6,00
|
84,00
|
1,92
|
170,00
|
2,23
|
|
7,00
|
55,00
|
1,74
|
104,00
|
2,02
|
|
8,00
|
67,00
|
1,83
|
132,00
|
2,12
|
|
9,00
|
81,00
|
1,91
|
159,00
|
2,20
|
|
10,00
|
59,00
|
1,77
|
116,00
|
2,06
|
|
сумма
|
706,00
|
18,44
|
1391,00
|
21,37
|
|
среднее
|
70,60
|
1,84
|
139,10
|
2,14
|
Обозначим Y=lg(y), X=lg(x),
A=lg(a). Тогда имеем уравнение: Y=A+bX – линейное уравнение регрессии.
Рассчитаем его параметры, используя таблицу 3.3:
Табл. 3.3
|
Наблюд
ение
|
x
|
X=lg(x)
|
y
|
Y=lg(y)
|
YX
|
X^2
|
y'
|
e
|
[e/y]*100%
|
e^2
|
|
1
|
66
|
1,82
|
133
|
2,12
|
3,8584
|
3,3124
|
136,3901
|
-3,3901
|
2,548945
|
11,49276
|
|
2
|
58
|
1,76
|
107
|
2,03
|
3,5728
|
3,0976
|
131,96869
|
-24,9687
|
23,335223
|
623,4354
|
|
3
|
73
|
1,86
|
145
|
2,16
|
4,0176
|
3,4596
|
139,94208
|
5,057923
|
3,4882229
|
25,58259
|
|
4
|
82
|
1,91
|
162
|
2,21
|
4,2211
|
3,6481
|
144,15365
|
17,84635
|
11,016263
|
318,4921
|
|
5
|
81
|
1,91
|
163
|
2,21
|
4,2211
|
3,6481
|
143,70325
|
19,29675
|
11,8385
|
372,3648
|
|
6
|
84
|
1,92
|
170
|
2,23
|
4,2816
|
3,6864
|
145,04233
|
24,95767
|
14,68098
|
622,8851
|
|
7
|
55
|
1,74
|
104
|
2,02
|
3,5148
|
3,0276
|
130,19319
|
-26,1932
|
25,185761
|
686,0833
|
|
8
|
67
|
1,83
|
132
|
2,12
|
3,8796
|
3,3489
|
136,9142
|
-4,9142
|
3,7228769
|
24,14934
|
|
9
|
81
|
1,91
|
159
|
2,2
|
4,202
|
3,6481
|
143,70325
|
15,29675
|
9,6206006
|
233,9907
|
|
10
|
59
|
1,77
|
116
|
2,06
|
3,6462
|
3,1329
|
132,5453
|
-16,5453
|
14,263191
|
273,747
|
|
сумма
|
706,00
|
18,44
|
1391,00
|
21,37
|
39,42
|
34,01
|
1384,56
|
6,44
|
119,70
|
3192,22
|
|
среднее
|
70,60
|
1,84
|
139,10
|
2,14
|
3,94
|
3,40
|
138,46
|
0,64
|
11,97
|
319,22
|
b=(Y*X-Y*X)/ X2-X2=(3,94152-1,84*2,14)/3,40097-1,84*1,84=0,00392/0,01537
= 0,25504229
a=y-b*x=2,14-0,25504229*1,84=1,670722186
Y=1,670722186+0,25504229*x
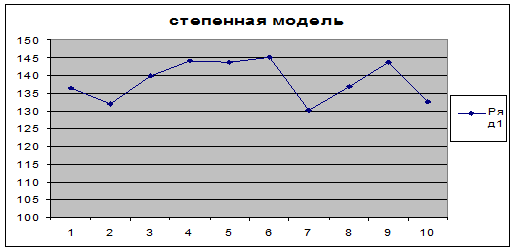
Получим следующее уравнение степенной модели:
y’=101.670722186*x0.25504229=46,85135826*x0.25504229,
и её график:
Рис. 4
Показательная
модель
Уравнение показательной кривой: y’=a*bx; для построения этой модели
произведём линеаризацию переменных. Для этого осуществим логарифмирование обеих
частей уравнения: lg(y’)=lg(a)+lg(x)*b
Обозначим: Y=lg(y’) , B=lg(b) , A=lg(a)
Получим линейное уравнение регрессии:
Y=A+B*x.
Рассчитаем
его параметры, используя данные таблицы 3.4:
Табл.3.4
|
Наблю
дение
|
x
|
y
|
Y=lg(y)
|
Y*x
|
x^2
|
(Y-Ycp)^2
|
x-xcp
|
(x-xcp)^2
|
|
1
|
66
|
133
|
2,12
|
139,92
|
4356
|
0,0004
|
-4,60
|
21,16
|
|
2
|
58
|
107
|
2,03
|
117,74
|
3364
|
0,0121
|
-12,60
|
158,76
|
|
3
|
73
|
145
|
2,16
|
157,68
|
5329
|
0,0004
|
2,40
|
5,76
|
|
4
|
82
|
162
|
2,21
|
181,22
|
6724
|
0,0049
|
11,40
|
129,96
|
|
5
|
81
|
163
|
2,21
|
179,01
|
6561
|
0,0049
|
10,40
|
108,16
|
|
6
|
84
|
170
|
2,23
|
187,32
|
7056
|
0,0081
|
13,40
|
179,56
|
|
7
|
55
|
104
|
2,02
|
111,1
|
3025
|
0,0144
|
-15,60
|
243,36
|
|
8
|
67
|
132
|
2,12
|
142,04
|
4489
|
0,0004
|
-3,60
|
12,96
|
|
9
|
81
|
159
|
2,2
|
178,2
|
6561
|
0,0036
|
10,40
|
108,16
|
|
10
|
59
|
116
|
2,06
|
121,54
|
3481
|
0,0064
|
-11,60
|
134,56
|
|
сумма
|
706,00
|
1391,00
|
21,37
|
1515,77
|
50946
|
0,0556
|
0,00
|
1102,40
|
|
среднее
|
70,60
|
139,10
|
2,14
|
151,577
|
5094,6
|
0,00556
|
|
110,24
|
B=[Y*x-Y*x]/[x^2-x^2]=[151.577-2.14*70.60]/[5094.60-70.60*70.60]=0.496/110.24=
0.004472
A=Y-B*x=2.14-0.004472*70.60=1.82427
Уравнение будет иметь вид:
Y=1.82427+0.004472*x.
Перейдём к исходным переменным x и y, выполнив потенцирование данного
уравнения:
y’=101.82427*(100.004472)x=66.722*1.01035x, график показательной модели:
Рис. 5
9. Гиперболическая модель
Определим индекс корреляции,
с помощью таблицы 4.1:
Табл. 4.1
|
Наблюд
ение
|
x
|
y
|
X
|
y*X
|
X^2
|
y-ycp
|
(y-ycp)^2
|
y'
|
e
|
e^2=(y-y')^2
|
(e/y)*100
|
|
1
|
66
|
133,00
|
0,02
|
2,02
|
0,00
|
-6,10
|
37,21
|
132,31
|
0,69
|
0,48
|
0,52
|
|
2
|
58
|
107,00
|
0,02
|
1,84
|
0,00
|
-32,10
|
1030,41
|
110,72
|
-3,72
|
13,82
|
3,47
|
|
3
|
73
|
145,00
|
0,01
|
1,99
|
0,00
|
5,90
|
34,81
|
147,32
|
-2,32
|
5,36
|
1,60
|
|
4
|
82
|
162,00
|
0,01
|
1,98
|
0,00
|
22,90
|
524,41
|
162,85
|
-0,85
|
0,72
|
0,52
|
|
5
|
81
|
163,00
|
0,01
|
2,01
|
0,00
|
23,90
|
571,21
|
161,29
|
1,71
|
2,92
|
1,05
|
|
6
|
84
|
170,00
|
0,01
|
2,02
|
0,00
|
30,90
|
954,81
|
165,85
|
4,15
|
17,24
|
2,44
|
|
7
|
55
|
104,00
|
0,02
|
1,89
|
0,00
|
-35,10
|
1232,01
|
101,00
|
3,00
|
8,99
|
2,88
|
|
8
|
67
|
132,00
|
0,01
|
1,97
|
0,00
|
-7,10
|
50,41
|
134,64
|
-2,64
|
6,99
|
2,00
|
|
9
|
81
|
159,00
|
0,01
|
1,96
|
0,00
|
19,90
|
396,01
|
161,29
|
-2,29
|
5,26
|
1,44
|
|
10
|
59
|
116,00
|
0,02
|
1,97
|
0,00
|
-23,10
|
533,61
|
113,74
|
2,26
|
5,12
|
1,95
|
|
сумма
|
706
|
1391,00
|
0,14
|
19,65
|
0,00
|
0,00
|
5364,90
|
1391,00
|
0,00
|
66,89
|
17,88
|
|
среднее
|
70,6
|
139,10
|
0,01
|
1,96
|
0,00
|
|
536,49
|
139,10
|
|
6,69
|
1,79
|
ρyx=√1-[∑(y-y’)^2]/∑(y-ycp)^2 =0,9937
Связь между
показателем y и фактором x можно считать достаточно сильной.
Индекс детерминации:
R^2= ρyx^2=0,988
Вариация результата Y (объём выпуска продукции) на 98,8%
объясняется вариацией фактора X (объёмом капиталовложений).
Средняя относительная ошибка
аппроксимации:
A=[1/n]*∑|(y-yср)/y)|*100%=66,89/10=6,689%
В среднем расчетные значения y’ для степенной модели отличаются от
фактических значений на 6,689%.
Степенная модель
Определим индекс корреляции:
ρyx=√1-[∑(y-y’)^2]/∑(y-ycp)^2 = 0,63638
Связь между показателем y и фактором x можно считать умеренной.
Коэффициент детерминации:
R^2= ρyx^2=0,63638^2=0,40498
Вариация результата Y (объём выпуска продукции) на 40,498%
объясняется вариацией фактора X (объёмом капиталовложений).
Средняя относительная ошибка
аппроксимации:
A=[1/n]*∑|(y-yср)/y)|*100%=119,70/10=11,97%
В среднем расчетные значения y’ для степенной модели отличаются от фактических
значений на 11,97%.
Показательная модель
Определим индекс корреляции с
помощью таблицы 4.2:
табл.4.2
|
Наблюю
дение
|
x
|
X=lg(x)
|
y
|
Y=lg(y)
|
YX
|
X^2
|
y'
|
e
|
[e/y]*100%
|
e^2
|
|
1
|
66
|
1,82
|
133,00
|
2,12
|
3,86
|
3,31
|
131,65
|
1,35
|
1,02
|
1,83
|
|
2
|
58
|
1,76
|
107,00
|
2,03
|
3,57
|
3,10
|
121,24
|
-14,24
|
13,31
|
202,70
|
|
3
|
73
|
1,86
|
145,00
|
2,16
|
4,02
|
3,46
|
141,49
|
3,51
|
2,42
|
12,35
|
|
4
|
82
|
1,91
|
162,00
|
2,21
|
4,22
|
3,65
|
155,22
|
6,78
|
4,18
|
45,91
|
|
5
|
81
|
1,91
|
163,00
|
2,21
|
4,22
|
3,65
|
153,63
|
9,37
|
5,75
|
87,71
|
|
6
|
84
|
1,92
|
170,00
|
2,23
|
4,28
|
3,69
|
158,45
|
11,55
|
6,79
|
133,30
|
|
7
|
55
|
1,74
|
104,00
|
2,02
|
3,51
|
3,03
|
117,55
|
-13,55
|
13,03
|
183,59
|
|
8
|
67
|
1,83
|
132,00
|
2,12
|
3,88
|
3,35
|
133,01
|
-1,01
|
0,76
|
1,02
|
|
9
|
81
|
1,91
|
159,00
|
2,20
|
4,20
|
3,65
|
153,63
|
5,37
|
3,37
|
28,79
|
|
10
|
59
|
1,77
|
116,00
|
2,06
|
3,65
|
3,13
|
122,49
|
-6,49
|
5,60
|
42,15
|
|
сумма
|
706
|
18,44
|
1391,00
|
21,37
|
39,42
|
34,01
|
1388,37
|
2,63
|
56,23
|
739,34
|
|
среднее
|
70,6
|
1,84
|
139,10
|
2,14
|
3,94
|
3,40
|
138,84
|
0,26
|
5,62
|
73,93
|
ρyx=√1-[∑(y-y’)^2]/∑(y-ycp)^2 =0,9285
Связь между показателем y и фактором x можно считать достаточно сильной.
Индекс детерминации:
R^2= ρyx^2=0,9285^2=0,862
Вариация результата Y (объём выпуска продукции) на 86,2%
объясняется вариацией фактора X (объёмом капиталовложений).
Средняя относительная ошибка
аппроксимации:
A=[1/n]*∑|(y-yср)/y)|*100%=56,23/10=5,62%
В среднем расчетные значения y’ для степенной модели отличаются от
фактических значений на 5,62%.
Для выбора лучшей модели построим сводную таблицу
результатов:
|
параметры
модель
|
Коэффициент
Детерминации
R2
|
Индекс корреляции
ρyx
|
Средняя относительная ошибка аппроксимации
A
|
|
1. линейная
|
0,9889
|
0,9944
|
15,7%.
|
|
2.степенная
|
0,40498
|
0,63638
|
11,97%
|
|
3.показательная
|
0,862
|
0,9285
|
5,62%
|
|
4.гиперболическая
|
0,988
|
0,9937
|
6,689%
|
Линейная модель является лучшей для построения прогноза, т.к.
характеристики этой модели имеют большее значение, чем у других. Среди
нелинейных моделей наиболее точной является гиперболическая модель, в которой
значения показателей коэффициента детерминации и индекса корреляции больше, чем
у остальных нелинейных моделей.