3.3. Расчет
параметров настройки регулятора САР температуры сушки рыбной муки.
Динамические
характеристики САР заданы в виде передаточных функций в соответствии с
вариантом задания. Пользуясь частотными методами исследования динамики,
определим параметры настройки САР с пропорционально-интегральным регулятором.
Структурная
схема системы автоматического регулирования в соответствии с функциональной
схемой будет иметь вид:
Хр Хв
Хзад Хд
Wрег(S) Wo (S)
которую с учетом передаточных функций
объекта регулирования - WОБ(S), чувствительного элемента WЧЭ(S)
и регулирующего органа WРО(S) можно представить в виде:
Хв
Wo(S)
Xза
ХB
Wрег(S) Wро(S) Wоб(S) Wчэ(S)
Следовательно,
можно записать:
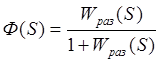
Расчет параметров САР выполним по АФХ
разомкнутой системы, для чего:
1) Строим АФХ
объекта регулирования.
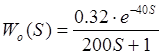
Заменяем S=iw,
получаем:
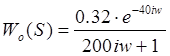
Освобождаясь от
мнимости в знаменателе и получим:
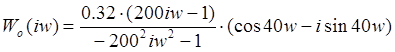
Где, е-40iw=cos40w-i sin40w (формула Эйлера).
Раскроем скобки и выделим вещественную и
мнимую составляющие.
где, 
вещественная часть АФХ,
мнимая часть АФХ.
Расчет АФХ
объекта регулирования выполним с помощью программного языка «BASIC» и полученные значения сведем в
таблицу 3.4. Построение АФХ объекта выполнено на формате А1 в координатах Re(w) и Im(w).
Построение АФХ
объекта разомкнутой системы с ПИ-регулятором производим в следующем порядке:
1)
на АФХ объекта регулирования выбираем несколько точек с
частотами w1, w2,
w3, ..., которые соединяем с началом координат отрезками ОА1,
ОА2, ...;
2)
в конце каждого вектора восстанавливаем перпендикуляры;
3)
на каждом перпендикуляре откладываем отрезки, равные.
Табл.3.3.
, 
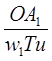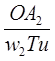
4)
соединяем концы отрезков плавной кривой, получаем АФХ
разомкнутой системы при Кр=1, и выбранном значении времени изодрома Ти;
5)
повторяем пункты 1 - 4, строим пять АФХ разомкнутой системы с
Кр=1 и с пятью различными значениями времени изодрома. Значения времени
изодрома (Ти) выбираем из технической характеристики заданного регулятора таким
образом, чтобы АФХ-ки при построении отстояли друг от друга;
6)
из начала координат проводим луч ОЕ под углом j к
отрицательной вещественной полуоси, равный
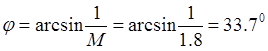
где М -
показатель колебательности, соответствующий заданному запасу устойчивости САР;
7)
строим пять окружностей с центром на отрицательной
вещественной полуоси, касающиеся луча ОЕ и АФХ разомкнутой системы с Кр=1 и
различными значениями Ти (Г. ч. 01);
8)
искомые значения коэффициентов передачи регулятора,
соответствующие различным значениям Ти, находятся по выражению:
;
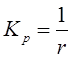где r- радиусы построенных
окружностей. Значения представлены в табл. 3.1.
Табл. 3.1.
|
Ти
|
Кр
|
|
80
|
11,11
|
|
100
|
13,33
|
|
120
|
14,7
|
|
140
|
16,66
|
|
160
|
18,18
|
9)
в координатах Кр - Ти строим область параметров настройки регулятора,
соответствующую заданному показателю колебательности рис.1.
10)
Для нахождения оптимальных параметров настройки регулятора из
начала координат проводим касательную к области, точка касания даст искомые
значения рис.1.
11)
Искомые значения коэффициентов передачи регулятора,
соответствующие критическому состоянию системы (система находится на грани
устойчивости), находятся как обратная величина отрезков отсекаемых на
отрицательной вещественной полуоси АФХ, разомкнутых систем
;
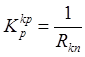где RKP -
отрезок от начала координат до точки пересечения АФХ разомкнутой
системы с отрицательной
вещественной полуосью. По полученным данным строим область
критических параметров настройки регулятора рис.2.
Значения представлены в табл. 3.2.
Таблица 3.2.
|
Ти
|
КрKP
|
|
80
|
20,83
|
|
100
|
22,22
|
|
120
|
23,25
|
|
140
|
25
|
|
160
|
26,32
|
Таблица 3.3.
|
ОАi
0,11
|
Ти (с)
80
|
w
0,015
|
В
0,09
|
|
0,0772
|
|
0,02
|
0,048
|
|
0,039
|
|
0,04
|
0,0125
|
|
0,11
|
100
|
0,015
|
0,073
|
|
0,0772
|
|
0,02
|
0,0385
|
|
0,039
|
|
0,04
|
0,01
|
|
0,11
|
120
|
0,015
|
0,061
|
|
0,0772
|
|
0,02
|
0,032
|
|
0,039
|
|
0,04
|
0,008
|
|
0,11
|
140
|
0,015
|
0,052
|
|
0,0772
|
|
0,02
|
0,0275
|
|
0,039
|
|
0,04
|
0,007
|
|
0,11
|
160
|
0,015
|
0,046
|
|
0,0772
|
|
0,02
|
0,024
|
|
0,039
|
|
0,04
|
0,00625
|