Курсовая работа
по дисциплине Статистика
на тему
Выборочный метод наблюдения в
социально-экономических исследованиях
|
Выполнил
|
|
Студент курса
|
|
группы
|
|
отделения
|
|
|
Руководитель
|
|
Санкт-Петербург
2007
Содержание
Содержание. 2
Введение. 3
Глава 1. Теоретические основы выборочного метода. 4
Выборочное исследование. 4
Виды
отбора при выборочном наблюдении. 8
Ошибки наблюдения. 14
Способы отбора единиц в выборочную совокупность. 14
Средняя и предельная ошибка для показателей
средней величины.. 17
Средняя и предельная ошибка для показателей доли. 21
Определение необходимого объема выборки. 22
Понятие о малой выборке. 23
Глава 2. Выборочное исследование предприятий
Санкт-Петербурга. 24
Средняя ошибка выборочной средней. 29
Заключение. 30
Литература. 32
Введение
Наиболее корректный статистический
анализ общественного процесса обеспечивают сведения о каждом его проявлении.
Или, говоря статистическим языком, полный анализ всей совокупности возможен
только при учете значения признака у каждой единицы совокупности. В качестве примера
такого анализа можно привести всеобщие переписи населения.
Однако, массовый характер
общественного явления часто влечет за собой невозможность исследования его в
полном объеме, т.е. во всех его проявлениях. В статистической науке разработан
специальный метод, позволяющей исследовать лишь часть явления, а результаты и
выводы транспонировать [1] на все явление в целом. Такой метод называется
«выборочное наблюдение». Основой метода выборочного наблюдения служит взаимосвязь
между единичным и общим, между частью и целым, которая существует в
общественных явлениях.
Исследуемая часть статистической
совокупности называется выборочной, а количество единиц, составляющих ее объем
принято обозначать n. Вся
совокупность называется генеральной, объем генеральной совокупности обычно обозначают
N.
Можно выделить ряд причин применения выборочного наблюдения:
·
недостаток
временных ресурсов (как для проведения обследования, так и для анализа полученного
большого объема данных);
·
недостаток
кадровых ресурсов, т.е. квалифицированных специалистов для проведения наблюдения
и анализа;
·
недостаток
материальных ресурсов, т.е. слишком дорогостоящее наблюдение;
·
практическая
невозможность учета всех единиц совокупности в связи с их уничтожением в
результате наблюдения (например, в случае обследования всхожести партии семян,
продолжительности горения электроламп и т.д.);
·
практическая
нецелесообразность наблюдения каждой единицы совокупности (например,
определения уровня потребления продукта питания населением региона и т.д.)
Основным принципом выборочного
наблюдения является принцип рэндомизации (от англ. random – случай), т.е.
принцип случайности отбора единиц совокупности, определяющий равенство единиц
по возможности быть отобранными в выборочную совокупность. Данный принцип
должен выполняться даже в случае планомерного отбора единиц.
В результате неполного обследования
генеральной совокупности могут возникнуть ошибки наблюдения – ошибки репрезентативности.
Поэтому, основной задачей исследователя является, во-первых, обеспечение
представительности (репрезентативности) выборки, и, во-вторых, определение
степени уверенности в соответствии параметров выборочной и генеральной совокупностей.
Задачи работы: описать теоретические основы
выборочного метода
Цель работы: с
помощью представленного метода
исследовать показатель «Дебиторская задолженность»
Глава 1.
Теоретические основы выборочного метода
Выборочное исследование
При статистическом исследовании
экономических явлений могут применяться выборочные
наблюдения, при которых характеристики генеральной совокупности получаются
на основании изучения части генеральной совокупности, называемой выборочной совокупностью или выборкой.
Выборочное
наблюдение (выборочное исследование)
заключается в обследовании определенного числа единиц совокупности, отобранного,
как правило, случайным образом. При выборочном методе обследованию подлежит
сравнительно небольшая часть всей изучаемой совокупности (обычно до 5–10%, реже
до 15–20%). Отбор единиц из генеральной совокупности производится таким
образом, чтобы выборочная совокупность была представительна
(репрезентативна) и
характеризовала генеральную совокупность. Степень представительности выборки
зависит от способа организации выборки и от ее объема. Полной
репрезентативности выборки достичь не удается. Поэтому необходима оценка
надежности результатов выборки и возможности их распространения на генеральную
совокупность.
В зависимости от характеристик выборочных
совокупностей выборки могут быть представительными,
расслоенными, засоренными и цензурированными.
Представительная
выборка – выборка наблюдений из генеральной совокупности, наиболее полно и
адекватно представляющая ее свойства [3].
Расслоенная
выборка – выборка, включающая ряд выборочных совокупностей, взятых из
соответствующих слоев генеральной совокупности. Широко используется при
выборочном обследовании в экономике, демографии и социологии.
Засоренная
выборка – выборка наблюдений, содержащая “грубые” ошибки. Основная масса
элементов засоренной выборки является реализацией случайной величины X , закон распределения которой известен. Такие
элементы – “типичные” – появляются в совокупности с вероятностью 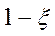 . С вероятностью
. С вероятностью 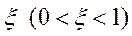 элементы совокупности
оказываются реализацией другой случайной величины Y , закон распределения которой в общем случае
неизвестен. Такие элементы называются “грубыми” ошибками. Обычные оценки,
например, средняя арифметическая выборочная, на засоренной выборке теряют свои
оптимальные свойства (эффективность, несмещенность) с ростом интенсивности
засорения
элементы совокупности
оказываются реализацией другой случайной величины Y , закон распределения которой в общем случае
неизвестен. Такие элементы называются “грубыми” ошибками. Обычные оценки,
например, средняя арифметическая выборочная, на засоренной выборке теряют свои
оптимальные свойства (эффективность, несмещенность) с ростом интенсивности
засорения 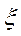 .
.
Цензурированная
выборка – выборка, полученная из вариационного ряда наблюдений путем отбрасывания
некоторого числа экстремальных наблюдений. Если отбрасывание производится по
признаку выхода наблюдений за пределы заданного интервала, то такой прием
называется цензурирование первого типа. В этом случае число оставшихся наблюдений
является случайной величиной. Если отбрасывается фиксированная доля 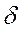 крайних малых значений
и фиксированная доля
крайних малых значений
и фиксированная доля 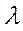 крайних больших
значений, то это называется цензурированием второго типа уровня
крайних больших
значений, то это называется цензурированием второго типа уровня 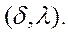 При этом, число
оставшихся в рассмотрении наблюдений является величиной заранее заданной.
При этом, число
оставшихся в рассмотрении наблюдений является величиной заранее заданной.
Проведение
выборочных исследований статистической информации состоит из следующих этапов:
·
формулировка цели статистического наблюдения;
·
обоснование целесообразности выборочного наблюдения;
·
отграничение генеральной совокупности;
·
установление системы отбора единиц для наблюдения;
·
определение числа единиц, подлежащих отбору;
·
проведение отбора единиц;
·
проведение наблюдения;
·
расчет выборочных характеристик и их ошибок;
·
распространение выборочных данных на генеральную
совокупность.
Выборочное исследование осуществляется с минимальными затратами труда и средств и в
более короткие сроки, чем сплошное наблюдение, что повышает оперативность
статистической информации, уменьшает ошибки регистрации. В проведении ряда
исследований выборочный метод является единственно возможным, например, при
контроле качества продукции, сопровождающимся разрушением проверяемого изделия.
Выборочный метод дает достаточно точные
результаты, поэтому он может применяться для проверки данных сплошного
наблюдения. Минимальная численность обследуемых единиц позволяет провести
исследование более тщательно и квалифицированно. Например, при переписях населения
практикуются выборочные контрольные наблюдения для проверки правильности записей
сплошного наблюдения.
В основе теории выборочного наблюдения
лежат теоремы законов больших чисел, которые позволяют решить два
взаимосвязанных вопроса выборки: рассчитать ее объем при заданной точности исследования и определить ошибку при данном объеме выборки.
При использовании выборочного метода
обычно используются два вида обобщающих показателей: относительную величину альтернативного признака и среднюю величину количественного признака.
Относительная величина альтернативного
признака характеризует долю (удельный
вес) единиц в статистической совокупности, обладающих изучаемым признаком. В
генеральной совокупности эта доля единиц называется генеральной долей (p), а в
выборочной совокупности – выборочной
долей (w).
Средняя величина количественного признака
в генеральной совокупности называется генеральной
средней ( 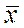 ), а в выборочной совокупности – выборочной средней (
), а в выборочной совокупности – выборочной средней (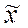 ).
).
Виды отбора при
выборочном наблюдении
Процесс образования выборки называется отбором, который осуществляется в
порядке беспристрастного, случайного отбора единиц из генеральной совокупности
[16].
Основным условием проведения выборочного
наблюдения является предупреждение возникновения систематических
(тенденциозных) ошибок, возникающих вследствие нарушения принципа равных
возможностей попадания в выборку каждой единицы совокупности. Предупреждение
систематических ошибок достигается в результате применения научно обоснованных способов
формирования выборочной совокупности. Существуют различные способы отбора: индивидуальный, групповой (серийный), комбинированный, повторный
(возвратный), бесповторный (безвозвратный),одноступенчатый,
многоступенчатый, собственно–случайный, механический, типический, двухфазный и многофазный отбор
При индивидуальном
отборе в выборку отбираются отдельные единицы совокупности. Отбор
повторяется столько раз, сколько необходимо отобрать единиц.
Групповой
(серийный) отбор заключается в отборе серий (например, отбор изделий для
проверки их целыми партиями). Если обследованию подвергаются все единицы
отобранных серий, отбор называется серийным,
а если обследуется только часть единиц каждой серии, отбираемых в индивидуальным
порядке из серии, то – комбинированным.
Если в процессе отбора отобранная единица
не исключается из совокупности, т.е. возвращается в совокупность, и может быть
повторно отобранной, то такой отбор называется повторным или возвратным,
в противном случае – бесповторным
или безвозвратным. Серийный отбор,
как правило, безвозвратный[1].
При одноступенчатом
отбираются единицы совокупности (или серии) непосредственно для наблюдения. При
многоступенчатом отбираются сначала
крупные серии единиц (первая ступень отбора), наблюдению они не подвергаются.
Затем из них отбираются серии, меньшие по численности единиц (вторая ступень),
наблюдению не подвергаются, и так до тех пор, пока не будут отобраны те единицы
совокупности (серии), которые будут подвергнуты наблюдению [5].
Собственно–случайный
отбор состоит в отборе единиц (серий) из всей генеральной совокупности в целом
посредством жеребьевки или на основании таблиц случайных чисел.
Жеребьевка
состоит в том, что на каждую единицу отбора составляется карточка, которой присуждается
порядковый номер. После тщательного перемешивания по очереди извлекаются
карточки, пока не будет отобрано требуемое число единиц.
Случайными
числами называются ряды чисел, являющихся реализациями последовательности
взаимно независимых и одинаково распределенных случайных величин. Эти
последовательности чисел получаются либо с помощью физических генераторов (подбрасывание кубиков с нанесенными на их
сторонами цифрами; вытягиванием из урны карточек с написанными на них цифрами,
преобразование случайных сигналов и др. физико–технические процессы), либо с
помощью программных генераторов
(аналитическим методом с помощью программ для ЭВМ). Числа, являющиеся
результатами соответствующей вычислительной процедуры, называются псевдослучайными числами. Последовательность
псевдослучайных чисел носит детерминированный характер, но в определенных
границах она удовлетворяет свойствам равномерного распределения и свойству случайности.
Случайные числа могут быть
выбраны по таблице случайных чисел (приложение 1), которая содержит 2000
случайных чисел, объединенных для удобства пользования таблицей в 500 блоков по
4 значения) Например,
5489, 5583, 3156, 0835, 1988, 3912.
Применение комбинаций этих
цифр зависит от размера совокупности: если в генеральной совокупности 1000
единиц, то порядковый номер каждой единицы должен состоять из двух цифр от 000
до 999. В этом случае первые 8 номеров единиц выборочной совокупности
следующие:
548, 955, 833, 156, 083, 519, 883, 912.
При произвольном объеме
генеральной совокупности, отличающегося от 100, 1000, 10000 могут
использоваться псевдослучайные числа, сформированные на ЭВМ, или из таблицы
случайных чисел формируется последовательность случайных величин,
распределенных в интервале от 0 до 1. Например, в приведенном выше примере
0,5489; 0,5583; 0,3156; 0,0835; 0,1988; 0,3912 и т.д.
Если генеральная
совокупность состоит из 2000 единиц, то в выборочную совокупность должны войти
единицы с номерами:
2000 × 0,5489 = 1097,8 или 1099;
2000 × 0,5583 = 1116,6 или 1117;
2000 × 0,3156 =
631,2 или 631;
2000 × 0,0835 =
167,0 или 167;
2000 × 0,1988 =
397,6 или 398;
2000 × 0,3912 =
782,4 или 782.
Процесс формирования
случайных чисел и определения номера отбираемой единицы продолжается до тех
пор, пока не будет получен заданный объем выборочной совокупности.
Можно предложить другой
способ случайного отбора единиц в выборку. Допустим, что выборка состоит из 75 единиц, а генеральная
совокупность - из 780. Из таблицы случайных чисел выбираются, например,
следующие
5489, 5583, 3156, 0835, 1988, 3912.
В выборку могут войти
только единицы, порядковые номера которых равны трехзначным числам меньше 780.
Поэтому, используя только три последние цифры каждого числа, отбирается необходимые
75 номеров: 489, 583, 156 и т.д. Можно использовать и первые три цифры каждого
числа, тогда отобранные номера: 548, 558, 315, 83, 198, 391. Можно разбить
случайные четырехзначные случайные числа на ряд, состоящий из трехзначных
чисел:
548, 955, 833, 156,
083, 519, 883, 912
и отобрать из
них номера, которые меньше 780, а именно: 548, 156, 83, 519.
Механический
отбор заключается в том, что составляется список единиц генеральной
совокупности и в зависимости от числа отбираемых единиц (серий) устанавливается
шаг отбора, т.е. через какой интервал следует брать для наблюдения единицы
(серии). Например, в простейшем случае, при
10%–м отборе, отбирается каждая десятая единица по этому списку, т.е. если
первой взята единица за № 1, то следующими отбираются 11–я, 21–я и т.д. В такой
последовательности производится отбор, если единицы совокупности расположены в
списке без учета их “рангов”, т.е. значимости по изучаемым признакам. Начало
отбора в этом случае не имеет значения, его можно начать в приведенном примере
от любой единицы из первого десятка. При расположении единиц совокупности в
ранжированном порядке за начало отбора должна быть принята середина интервала
(шага отбора) во избежание систематической ошибки выборки[2].
При типическом
отборе генеральная совокупность разбивается на типические группы единиц по
какому–либо признаку (формируются однородные совокупности), а затем
из каждой из них производится механический или собственно–случайный отбор [14].
Отбор единиц из типов производится тремя методами: пропорционально численности
единиц типических групп, непропорционально численности единиц типических групп
и пропорционально колеблемости признака в группах.
В целях экономии средств
данные по некоторым интересующим исследователя признакам можно анализировать на
основании изучения всех единиц выборочной совокупности, а по другим признакам -
на основании части единиц выборочной совокупности, которые представляют
подвыборку из единиц первоначальной выборки. Этот метод называется двухфазным отбором. При наличии
нескольких подвыборок - метод
многофазного отбора.
Многофазный отбор по своей
структуре отличается от многоступенчатого отбора, так при многофазном отборе
используются на каждой фазе одни и те же отобранные единицы, при многоступенчатом
отборе на разных ступенях применяются единицы отбора разных порядков.
Многофазным отбором чаще всего пользуются в тех случаях, когда различно число
единиц, необходимых для определения отдельных показателей с заданной точностью.
Это связано как с различиями в степени колеблемости признаков, так и с разной
точностью, требуемой для расчетов. Ошибки при многофазной выборке
рассчитываются на каждой фазе отдельно [7].
Все виды отбора, поскольку
они могут быть повторными или бесповторными, имеют разновидности (табл.1)
Таблица1
|
Вид отбора
|
Разновидности
отбора в зависимости от
|
|
повторяемости
отбора единиц совокупности
|
от величины серий или пропорциональности отбора единиц совокупности
в группах
|
|
Собственно случайный
|
1. Собственно случайный
повторный
2. Собственно случайный
бесповторный
|
|
|
Механический
|
1. Механический
повторный
2. Механический
бесповторный
|
|
|
Серийный
|
1. Серийный с повторным
отбором серий
2. Серийный с бесповтор-
ным отбором
серий
|
1.1. Серийный с повторным отбором
равновеликих
серий
1.2. Серийный с повторным отбором
неравновеликих
серий
2.1. Серийный с бесповторном отбором
равновеликих
серий
2.2. Серийный с бесповторном отбором
неравновеликих
серий
|
|
Комбиниро-ванный
|
1. Комбинированный с
повторным
отбором
серий
2. Комбинированный с
бесповторным
отбором
серий
|
1.1. Комбинированный с повторным
отбором
равновеликих серий
1.2. Комбинированный с повторным
отбором
неравновеликих серий
2.1. Комбинированный с бесповторным
отбором
равновеликих серий
2.2. Комбинированный с бесповторным
отбором
неравновеликих серий
|
|
Типический
|
1. Типический с повторным
случайном отборе
внутри
групп
2. Типический при
бесповторном случайном отборе
внутри групп
|
1.1. Типический с повторным случайном
отборе
внутри групп, пропорциональ-
ном объему
групп
1.2. Типический с повторным случайном
отборе
внутри групп, непропорцио-
нальном
объему групп
1.3. Типический с повторным случайном
отборе
внутри групп, пропорциональ-
ном
колеблемости в группах
2.1. Типический с бесповторным случайном
отборе
внутри групп, пропорциональ-
ном объему
групп
2.2. Типический с бесповторным случайном
отборе внутри групп, непропорцио-
нальном
объему групп
2.3. Типический
бесповторным случайном
отборе
внутри групп, пропорциональ-
ном
колеблемости в группах
|
1. По охвату единиц совокупности:
·
сплошное;
·
несплошное
(выборочное, монографическое, по методу основного массива)
2. По времени регистрации фактов:
·
текущее
(непрерывное);
·
прерывное
(периодическое, единовременное)
3. По способу сбора информации:
·
непосредственное
наблюдение;
·
документальное
наблюдение;
·
опрос
(анкетный, корреспондентский и др.)
Ошибки наблюдения
При большом числе единиц
исследуемой совокупности ошибки и неточности могут погашаться, однако, если
применяется выборочное наблюдение, тогда ошибки могут существенно повлиять на
результаты исследования.
В ходе наблюдения могут
возникнуть следующие ошибки:
1. Ошибки регистрации – ошибочные результаты наблюдения, полученные в результате недостаточной
квалификации исследователя, неточности измерительных приборов, некорректности
подсчетов и т.д.
2. Ошибки могут быть случайными и
систематическими [12].
·
Систематические
ошибки репрезентативности – ошибки, вызванные нарушением правил выбора единиц
совокупности для наблюдения;
·
Ошибки
репрезентативности (случайные) – ошибки, отражающие несовпадение выводов о
части явления с выводами о явлении в целом. Такие ошибки возникают при
применении несплошного метода наблюдения, случайные ошибки репрезентативности –
ошибки, отражающие неравномерное распределение единиц в совокупности, в связи с
чем, выборочная совокупность не корректно характеризует генеральную совокупность.
Способы отбора единиц в
выборочную совокупность
Определение способа отбора единиц
совокупности является важной частью выборочного исследования [9]. Существует
множество способов отбора единиц совокупности, все их можно представить в виде
трех групп (см. рис. 1.):
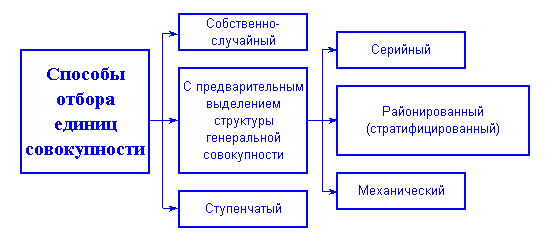 Рис. 1.
Рис. 1.
Собственно-случайный отбор – выбор единиц совокупности без какой-либо схемы или
системы. Может осуществляться методом жеребьевки или с помощью таблицы
случайных чисел. При применении данного способа отбора необходимо
удостовериться в выполнении принципа рэндомизации.
Отбор с предварительным выделением структуры генеральной совокупности
применяется, если исследуется структурированная (распределенная на группы)
совокупность. Серийный отбор предполагает выбор одной группы единиц, внутри
которой производится сплошное обследование, среди всех групп. Районированный
отбор представляет собой определение границ выборочной совокупности с учетом
территориальной принадлежности единиц генеральной совокупности. Механический
отбор применяется для совокупности, в которой каждой единице присвоен отдельный
номер, а выбор осуществляется пропорционально количеству единиц, например,
каждая десятая единица и др [10].
Ступенчатый или смешанный отбор применяется в случае поэтапного проведения выборочного
наблюдения, когда на разных этапах наблюдения используют различные варианты отбора
единиц.
Все приведенные выше способы, с точки
зрения математической статистики, делятся на повторные и бесповторные.
Повторный отбор предоставляет единице совокупности возможность быть отобранной
еще один или несколько раз при условии сохранения принципа рэндомизации. Соответственно,
бесповторным называется отбор, при котором единица, будучи однажды
исследованной, исключается из генеральной совокупности. Тем самым, устраняется
возможность ее повторного отбора в качестве представителя генеральной
совокупности [11]. Отличие в методах повторного и бесповторного отбора
математически отображают с помощью поправочного коэффициента на бесповторность
(К):
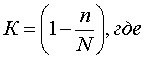
n – численность единиц выборочной совокупности; N – численность единиц генеральной
совокупности.
В математической статистике
разработана методика анализа выборочного наблюдения случайных явлений. Основой
такого анализа является предположение о множественности производимых выборочных
наблюдений, и, как следствие, построение целого ряда распределения вероятностей
различных характеристик полученных выборок[3].
Предполагается осуществление только отдельного выборочного наблюдения.
Результаты выборочного наблюдения
должны быть корректно перенесены на генеральную совокупность. При применении
выборочного метода всегда происходит погашение особенностей отдельных единиц
генеральной совокупности. Именно поэтому предполагается несоответствие
параметров генеральной совокупности параметрам выборочной, т.е. наличие больших
или меньших ошибок наблюдения. Чтобы исключить такое несоответствие параметры
генеральной совокупности обычно представляют не с помощью отдельного значения,
а в виде границ интервала, в пределах которого могут происходить колебания
параметров.
Применение выборочного исследования
предполагает определение параметров совокупности с некоторой степенью точности.
Причем, точность зависит от меры репрезентативности выборки относительно генеральной
совокупности, т.е. от качества выборочных данных. Чем хуже представлена в
выборке генеральная совокупность, тем меньше степень точности выводов. Следовательно,
тем дальше должны быть «раздвинуты» пределы интервала, в которых может
колебаться параметр генеральной совокупности.
Еще одним определителем степени
точности выводов служит их последующее применение. То есть, чем более
корректные данные о генеральной совокупности требуется получить, тем дальше
«раздвигаются» пределы интервала. Например, если исследование проводится в
целях обучения студентов методике выборки, то принимается условная (низкая)
степень точности. Тогда как, исследование, необходимое для государственного
управления, предполагает высокую степень точности.
Средняя и предельная
ошибка для показателей средней величины
Обобщающей характеристикой
совокупности по изучаемому признаку является средняя величина признака.
Поэтому, как правило, сначала рассчитывают среднее значение признака для
выборочной совокупности ( 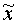 ), а затем,
исходя из меры соответствия между генеральной и выборочной совокупностями,
определяют пределы, в которых может колебаться среднее значение признака в генеральной
совокупности (
), а затем,
исходя из меры соответствия между генеральной и выборочной совокупностями,
определяют пределы, в которых может колебаться среднее значение признака в генеральной
совокупности ( 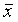 ).
).
Поскольку точные характеристики
генеральной совокупности не определены, то указать единичное значение
расхождения между средними для выборочной и генеральной совокупностей
невозможно. В связи с этим, определяют средний размер всех возможных ошибок (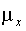 )
выборочного наблюдения. Другими словами, показатель
)
выборочного наблюдения. Другими словами, показатель 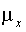 называется
средняя ошибка выборочной средней. Для повторного отбора
[8]:
называется
средняя ошибка выборочной средней. Для повторного отбора
[8]:
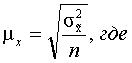
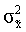 – дисперсия
выборочной совокупности;
– дисперсия
выборочной совокупности;
n – численность единиц выборочной
совокупности [13].
С применением поправочного
коэффициента на бесповторность средняя ошибка выборочной средней для
бесповторного отбора будет определяться следующим образом:
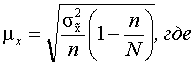
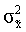 – дисперсия
выборочной совокупности;
– дисперсия
выборочной совокупности;
N – численность единиц генеральной
совокупности.
То есть, средняя в генеральной совокупности может отклониться
от средней в выборочной совокупности в сторону увеличения или уменьшения на величину
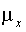 .
.
Предельная ошибка выборочной средней
( 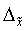 )
определяет границы, в пределах которых может колебаться среднее значение генеральной
совокупности относительно среднего значения выборки. Различия между средней и
предельной ошибкой обусловлены величиной коэффициента доверия t.
)
определяет границы, в пределах которых может колебаться среднее значение генеральной
совокупности относительно среднего значения выборки. Различия между средней и
предельной ошибкой обусловлены величиной коэффициента доверия t.
Суть этого коэффициента можно определить как ряд следующих
заключений:
·
предполагается
наличие расхождения между параметрами выборки и параметрами генеральной
совокупности, которое называется ошибкой;
·
предполагается,
что вместо полученных определенных результатов выборки, могли быть другие,
несколько отличные результаты, и, следовательно, могли быть другие
характеристики выборочной совокупности и другие ошибки [15];
·
предполагается
образование ряда распределения из возможных ошибок, причем, в таком ряду
рассчитывается среднее значение – средняя ошибка выборки (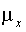 );
);
·
предполагается
наличие степени вероятности Р у каждой ошибки в этом ряду распределения;
·
предполагается
формирование распределения вероятностей ошибок Р(t), т.е. определение плотности
вероятности ошибок (графическое изображение см. рис 2.);
·
предполагается
более высокая вероятность появления ошибок определенного размера (среднего
размера ошибки) (графически отображается в виде возвышения «волны»,
характеризующей вероятность, см. рис. 2.);
·
по
оси абсцисс на графике откладывается значение t; тогда, чем ближе вероятность
ошибки расположена к оси ординат (соответственно, к вероятности появления
средней ошибки), тем меньше значение t.
·
в
зависимости от степени репрезентативности («доверия») выборочных данных, определяется
значение t, от величины которого зависит вероятность появления ошибок других
размеров, отличных от средней ошибки, следовательно, зависят границы колебания
значения параметров генеральной совокупности относительно выборки [6].
Таким образом, количественное выражение t, в конечном итоге,
является мерой «доверия» к реальности выборочных данных. Тогда предельная
ошибка выборочной средней (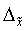 ) будет
определяться следующим образом:
) будет
определяться следующим образом:
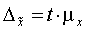 .
.
Отсюда, среднее значение генеральной совокупности имеет вид:
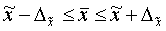
В статистике существуют наиболее
распространенные уровни вероятностей, например: 0,954; 0,997 и др. Это
означает, что, соответственно, в 6 случаях из 1000 и в 3 случаях из 1000 ошибка
выборки может превысить пределы, определенные выборочным наблюдением.
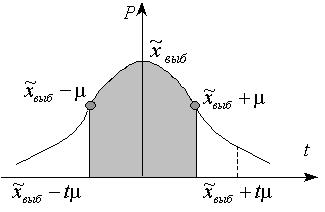
Рис. 2.
На рисунке 2. затемненная площадь под кривой показывает
вероятность появления средней ошибки выборочной средней. Площадь фигуры, образованной
перпендикулярами, опущенными на ось абсцисс[4], и
кривой плотности вероятности определяет вероятность появления предельной ошибки
выборочной средней [17].
Средняя и предельная
ошибка для показателей доли
Анализ генеральной совокупности не
ограничивается расчетом средних величин. Для характеристики распространенности
единиц совокупности с тем или иным значением изучаемого признака рассчитываются
показатели структуры (доли).
Принцип транспонирования выводов о
выборке на генеральную совокупность, принятый для средних величин, сохраняется
и при определении показателей доли:
1. Средняя ошибка выборки (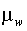 )для доли
(w) единиц, обладающих изучаемым признаком, при повторном отборе:
)для доли
(w) единиц, обладающих изучаемым признаком, при повторном отборе:
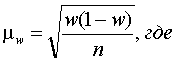
w – удельный вес единиц, обладающих изучаемым признаком;
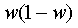 – дисперсия
для показателя доли;
– дисперсия
для показателя доли;
n – численность единиц выборочной
совокупности.
2. Средняя ошибка выборки (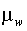 )для доли
(w) единиц, при бесповторном отборе:
)для доли
(w) единиц, при бесповторном отборе:
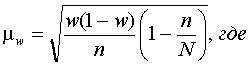
N – численность единиц генеральной
совокупности.
3. Предельная ошибка выборочной доли ( 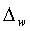 ):
):
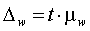 Тогда, удельный вес единиц, обладающих изучаемым признаком, в генеральной
совокупности будет находиться в пределах:
Тогда, удельный вес единиц, обладающих изучаемым признаком, в генеральной
совокупности будет находиться в пределах: 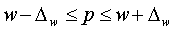
Определение необходимого
объема выборки
Прежде чем приступить к осуществлению
выборочного наблюдения необходимо определить количество единиц выборочной
совокупности, обеспечивающее репрезентативность, и, следовательно, надежность результатов
исследования [4].
На практике для реализации выборочного наблюдения
исследователем задаются:
·
степень
точности исследования (вероятность);
·
предельная
ошибка, т.е. интервал отклонения, определяемый целями исследования.
Исходя из этих критериев,
рассчитывается необходимая численность выборочной совокупности (n) на основе
формулы предельной ошибки выборки. Как указывалось выше, предельная ошибка
выборки определяется для средней величины ( 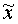 ) и для
доли (w), то, соответственно, имеем два варианта определения необходимой
численности выборочной совокупности:
) и для
доли (w), то, соответственно, имеем два варианта определения необходимой
численности выборочной совокупности:
а) для повторного отбора:
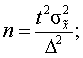
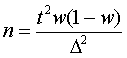
б)
для бесповторного отбора:
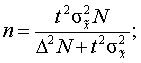
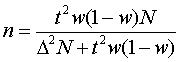
Понятие о малой выборке
В практике статистического
исследования иногда необходимо сделать выводы по малому числу наблюдений. Это
может быть связано с ограниченностью ресурсов на проведение выборки, или с
ограниченным доступом к объекту исследования. Если число наблюдений (единиц
выборочной совокупности) не превышает 30, то выборка называется малой. Расчет
показателей для малой выборки осуществляется с применением специальной
методики, учитывающей распределение вероятностей появления ошибок определенных
размеров. Напротив, в выборочной совокупности с большим количеством единиц
распределение ошибок предполагается нормальным или близким к нормальному.
Глава 2.
Выборочное исследование предприятий Санкт-Петербурга
Рассмотрим данные по 50
предприятиям
|
№ наблюдений
|
Собственные оборотные средства, млн.руб.
|
Балансовая прибыль, млн.руб.
|
Дебиторская задолженность, млн.руб.
|
Дивиденды, начисленные по результатам деятельности,
млн.руб.
|
курсовая цена акции, руб.
|
|
1
|
1011
|
107
|
75
|
20,33
|
92
|
|
2
|
799
|
102
|
51
|
20,04
|
83
|
|
3
|
995
|
107
|
41
|
19,87
|
95
|
|
4
|
1243
|
122
|
42
|
20,48
|
124
|
|
5
|
1507
|
108
|
42
|
20,13
|
96
|
|
6
|
947
|
108
|
51
|
20,26
|
106
|
|
7
|
1015
|
97
|
52
|
19,89
|
70
|
|
8
|
1169
|
109
|
33
|
19,92
|
97
|
|
9
|
1051
|
101
|
45
|
19,78
|
76
|
|
10
|
1372
|
116
|
50
|
20,23
|
112
|
|
11
|
1463
|
113
|
43
|
20,46
|
113
|
|
12
|
684
|
112
|
50
|
20,07
|
109
|
|
13
|
1251
|
106
|
53
|
20,23
|
91
|
|
14
|
1376
|
111
|
73
|
20,26
|
95
|
|
15
|
1193
|
113
|
31
|
20,28
|
115
|
|
16
|
1386
|
122
|
50
|
20,52
|
114
|
|
17
|
1631
|
118
|
69
|
20,28
|
133
|
|
18
|
1735
|
119
|
54
|
19,97
|
116
|
|
19
|
1181
|
102
|
53
|
19,97
|
85
|
|
20
|
922
|
100
|
41
|
19,57
|
91
|
|
21
|
1281
|
103
|
43
|
19,94
|
82
|
|
22
|
1333
|
113
|
52
|
20,29
|
105
|
|
23
|
1632
|
124
|
64
|
20,83
|
124
|
|
24
|
635
|
95
|
56
|
19,59
|
70
|
|
25
|
949
|
102
|
67
|
19,76
|
84
|
|
26
|
788
|
112
|
42
|
20,19
|
106
|
|
27
|
1728
|
124
|
49
|
20,66
|
128
|
|
28
|
1773
|
116
|
54
|
19,95
|
105
|
|
29
|
1679
|
118
|
57
|
20,61
|
121
|
|
30
|
1085
|
100
|
41
|
20,03
|
79
|
|
31
|
1214
|
99
|
62
|
19,78
|
82
|
|
32
|
1422
|
107
|
68
|
20,22
|
80
|
|
33
|
523
|
87
|
51
|
19,78
|
37
|
|
34
|
1025
|
109
|
65
|
20,09
|
101
|
|
35
|
1083
|
106
|
44
|
20,13
|
98
|
|
36
|
1466
|
113
|
54
|
20,56
|
98
|
|
37
|
1642
|
123
|
54
|
20,51
|
134
|
|
38
|
387
|
82
|
44
|
19,71
|
39
|
|
39
|
704
|
104
|
50
|
20,1
|
88
|
|
40
|
1177
|
112
|
50
|
20,32
|
108
|
|
41
|
1792
|
116
|
42
|
20,37
|
112
|
|
42
|
2072
|
106
|
59
|
20,03
|
80
|
|
43
|
1178
|
120
|
43
|
20,65
|
120
|
|
44
|
1304
|
105
|
58
|
20,19
|
88
|
|
45
|
1308
|
114
|
50
|
20,24
|
104
|
|
46
|
1416
|
107
|
49
|
20,27
|
94
|
|
47
|
1185
|
115
|
49
|
20,69
|
107
|
|
48
|
1220
|
96
|
57
|
19,85
|
82
|
|
49
|
1311
|
104
|
67
|
19,87
|
84
|
|
50
|
1288
|
108
|
54
|
20,2
|
101
|
Изучим показатель дебиторской
задолженности предприятий. Изучим параметры распределения этого показателя.
|
данные
|
номер
|
сортируем X
|
|X-Xсреднее|
|
(X-Xреднее)^2
|
(X-Xсреднее)^3
|
(X-Xреднее)^4
|
число наблюдений на интервале
|
|
75
|
1
|
31
|
20,88
|
435,9744
|
-9103,145472
|
190073,6775
|
3
|
|
51
|
2
|
33
|
18,88
|
356,4544
|
-6729,859072
|
127059,7393
|
|
41
|
3
|
41
|
10,88
|
118,3744
|
-1287,913472
|
14012,49858
|
|
42
|
4
|
41
|
10,88
|
118,3744
|
-1287,913472
|
14012,49858
|
7
|
|
42
|
5
|
41
|
10,88
|
118,3744
|
-1287,913472
|
14012,49858
|
|
51
|
6
|
42
|
9,88
|
97,6144
|
-964,430272
|
9528,571087
|
|
52
|
7
|
42
|
9,88
|
97,6144
|
-964,430272
|
9528,571087
|
|
33
|
8
|
42
|
9,88
|
97,6144
|
-964,430272
|
9528,571087
|
|
45
|
9
|
42
|
9,88
|
97,6144
|
-964,430272
|
9528,571087
|
|
50
|
10
|
43
|
8,88
|
78,8544
|
-700,227072
|
6218,016399
|
|
43
|
11
|
43
|
8,88
|
78,8544
|
-700,227072
|
6218,016399
|
8
|
|
50
|
12
|
43
|
8,88
|
78,8544
|
-700,227072
|
6218,016399
|
|
53
|
13
|
44
|
7,88
|
62,0944
|
-489,303872
|
3855,714511
|
|
73
|
14
|
44
|
7,88
|
62,0944
|
-489,303872
|
3855,714511
|
|
31
|
15
|
45
|
6,88
|
47,3344
|
-325,660672
|
2240,545423
|
|
50
|
16
|
49
|
2,88
|
8,2944
|
-23,887872
|
68,79707136
|
|
69
|
17
|
49
|
2,88
|
8,2944
|
-23,887872
|
68,79707136
|
|
54
|
18
|
49
|
2,88
|
8,2944
|
-23,887872
|
68,79707136
|
|
53
|
19
|
50
|
1,88
|
3,5344
|
-6,644672
|
12,49198336
|
19
|
|
41
|
20
|
50
|
1,88
|
3,5344
|
-6,644672
|
12,49198336
|
|
43
|
21
|
50
|
1,88
|
3,5344
|
-6,644672
|
12,49198336
|
|
52
|
22
|
50
|
1,88
|
3,5344
|
-6,644672
|
12,49198336
|
|
64
|
23
|
50
|
1,88
|
3,5344
|
-6,644672
|
12,49198336
|
|
56
|
24
|
50
|
1,88
|
3,5344
|
-6,644672
|
12,49198336
|
|
67
|
25
|
51
|
0,88
|
0,7744
|
-0,681472
|
0,59969536
|
|
42
|
26
|
51
|
0,88
|
0,7744
|
-0,681472
|
0,59969536
|
|
49
|
27
|
51
|
0,88
|
0,7744
|
-0,681472
|
0,59969536
|
|
54
|
28
|
52
|
0,12
|
0,0144
|
0,001728
|
0,00020736
|
|
57
|
29
|
52
|
0,12
|
0,0144
|
0,001728
|
0,00020736
|
|
41
|
30
|
53
|
1,12
|
1,2544
|
1,404928
|
1,57351936
|
|
62
|
31
|
53
|
1,12
|
1,2544
|
1,404928
|
1,57351936
|
|
68
|
32
|
54
|
2,12
|
4,4944
|
9,528128
|
20,19963136
|
|
51
|
33
|
54
|
2,12
|
4,4944
|
9,528128
|
20,19963136
|
|
65
|
34
|
54
|
2,12
|
4,4944
|
9,528128
|
20,19963136
|
|
44
|
35
|
54
|
2,12
|
4,4944
|
9,528128
|
20,19963136
|
|
54
|
36
|
54
|
2,12
|
4,4944
|
9,528128
|
20,19963136
|
|
54
|
37
|
56
|
4,12
|
16,9744
|
69,934528
|
288,1302554
|
|
44
|
38
|
57
|
5,12
|
26,2144
|
134,217728
|
687,1947674
|
5
|
|
50
|
39
|
57
|
5,12
|
26,2144
|
134,217728
|
687,1947674
|
|
50
|
40
|
58
|
6,12
|
37,4544
|
229,220928
|
1402,832079
|
|
42
|
41
|
59
|
7,12
|
50,6944
|
360,944128
|
2569,922191
|
|
59
|
42
|
62
|
10,12
|
102,4144
|
1036,433728
|
10488,70933
|
|
43
|
43
|
64
|
12,12
|
146,8944
|
1780,360128
|
21577,96475
|
5
|
|
58
|
44
|
65
|
13,12
|
172,1344
|
2258,403328
|
29630,25166
|
|
50
|
45
|
67
|
15,12
|
228,6144
|
3456,649728
|
52264,54389
|
|
49
|
46
|
67
|
15,12
|
228,6144
|
3456,649728
|
52264,54389
|
|
49
|
47
|
68
|
16,12
|
259,8544
|
4188,852928
|
67524,3092
|
|
57
|
48
|
69
|
17,12
|
293,0944
|
5017,776128
|
85904,32731
|
3
|
|
67
|
49
|
73
|
21,12
|
446,0544
|
9420,668928
|
198964,5278
|
|
54
|
50
|
75
|
23,12
|
534,5344
|
12358,43533
|
285727,0248
|
|
сумма
|
|
2594
|
367,52
|
4589,28
|
16880,2272
|
1236259,985
|
|
|
среднее
|
|
51,88
|
7,3504
|
91,7856
|
337,604544
|
24725,1997
|
|
Параметры распределения представлены
в таблице
|
сводка параметров распределения
|
|
Минимум
|
31
|
|
Максимум
|
75
|
|
Размах
|
44
|
|
Среднее
|
51,88
|
|
Дисперсия
|
91,79
|
|
среднее линейное
отклонение
|
7,35
|
|
среднеквадратичное
отклонение
|
9,58
|
|
Медиана
|
51
|
|
Мода
|
50
|
|
Наблюдений
|
50
|
|
коэффициент вариации
=СКО/среднее
|
0,184666156
|
|
3-й момент
|
337,604544
|
|
4-й момент
|
24725,1997
|
|
ассиметрия = 3-й
момент/СКО^3
|
0,383925056
|
|
эксцесс=4-й момент/СКО^4-3
|
-0,065117589
|
|
по формуле Стреджеса
выберем разбиение на
|
7
|
интервалов
|
|
ширина интервала =
|
|
6,285714286
|
единиц
|
|
|
|
|
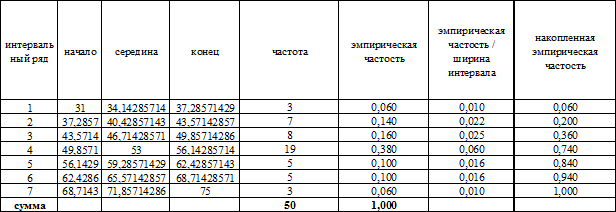
Эмпирическое распределение
представлено ниже на графиках
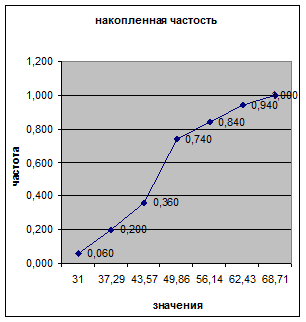
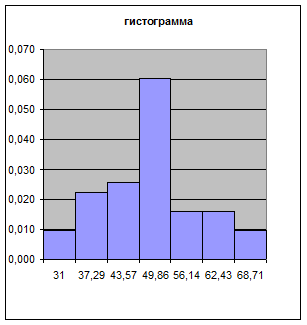
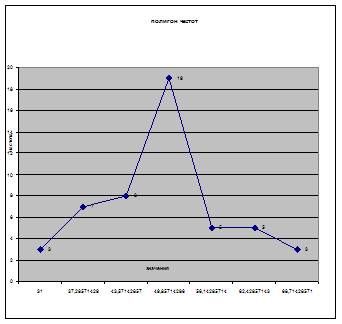
Проверка на нормальность по критерию Пирсона:
|
значение функции распределения на левом конце интервала
|
значение функции распределения на правом конце интервала
|
теоретическая частость - разность значений интегральных
функций распределений на концах интервалов
|
теоретическая частота
|
квадрат разности эмпирической и теоретической частоты
деленной на теоретическую частоту
|
|
0,015
|
0,064
|
0,04919
|
2,459
|
0,119
|
|
0,064
|
0,193
|
0,12907
|
6,453
|
0,046
|
|
0,193
|
0,416
|
0,22348
|
11,174
|
0,902
|
|
0,416
|
0,672
|
0,25544
|
12,772
|
3,037
|
|
0,672
|
0,865
|
0,19274
|
9,637
|
2,231
|
|
0,865
|
0,961
|
0,09599
|
4,800
|
0,008
|
|
0,961
|
0,992
|
0,03154
|
1,577
|
1,284
|
|
|
|
0,9774
|
|
7,627
|

Мы показали, что признак распределен
нормально. Значит и генеральная средняя тоже распределена нормально. Найдем
доверительный интервал для генеральной средней.
Средняя ошибка
выборочной средней
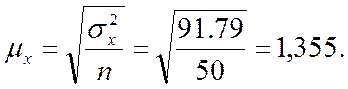
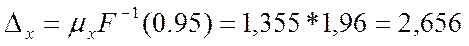
Тогда доверительный интервал
[51,88-2,656 ; 51,88+2,656]
или
[49.22 ;
54.54]
В найденном интервале с вероятностью
95% находится объем дебиторской задолженности.
Заключение
Одной
из задач, которые стоят перед исследователем при проведении исследования, является
сбор необходимых эмпирических данных об объекте исследования. Множество
элементов, составляющих объект исследования называют генеральной
совокупностью (ГС). Наиболее простым, на
первый взгляд, способом сбора данных является сплошное обследование ГС. Однако
применение сплошного обследования не всегда представляется возможным. В этом
случае применяется выборочное обследование. Суть выборочного метода заключена в
том, что обследованию подвергается только часть элементов ГС, которая
называется выборочной совокупностью (ВС). Изобретателем выборочного метода была
сама жизнь. Действительно, еще до теоретического обоснования возможностей
применения выборочного метода, статистики были вынуждены проводить выборочные
обследования. Основными причинами для этого были отсутствие времени и средств [2].
Выборочный метод позволяет не только сократить временные и
материальные затраты на проведения исследования, но и повысить достоверность
результатов исследования. Это утверждение может вызвать недоумение: как можно
получить более достоверные данные, обследовав меньшую часть ГС? Однако практика
показывает, что достоверность полученной информации при использовании
выборочного метода может быть не только не ниже, чем при сплошном обследовании,
но и выше вследствие возможности привлечения персонала более высокого класса и
применения различных процедур контроля качества получаемой информации.
Кроме того выборочный метод имеет более широкую область применения.
Широта области применения выборочного метода объясняется тем, что небольшой (по
сравнению с ГС) объем выборки позволяет использовать более сложные методы
обследования, включая использование различных технических средств (например,
видео- и аудиосредства, персональные компьютеры и Интернет, а также сложную
измерительную технику).
Выборочные обследования широко применяются в работе органов
государственной статистики. Чаще всего крупные и средние предприятия охватываются сплошным; наблюдением,
а наблюдение за деятельностью малых предприятий производится с помощью
выборочных обследований. В ряде случаев выборочные наблюдения применяются в
сочетании со сплошными переписями и учетами. Например, программа Всероссийской
переписи населения 2002г. содержит как вопросы сплошного наблюдения, относящиеся
ко всему населению, так и вопросы выборочного наблюдения 25% населения для
характеристики основного занятия, занимаемого положения, места работы, а также
вопросы 5%-ного выборочного обследования с целью изучения брачности и рождаемости.
Литература
1. Голуб Л. А.
Социально-экономическая статистика. 2003
2. Бурцева С. А. Статистика финансов. 2004
3. Громыко Г.Л.
Теория статистики. 2007
4. Елисеева И. И., Силаева С. А., Щирина А. Н. Практикум по макроэкономической
статистике. 2007
5. Елисеева И.И.
Общая теория статистики: Учебник для ВУЗов. – М.: Финансы и статистика, 2004.
6. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. -
М.: ИНФРА-М, 2002.
7. Ефимова М. Р., Бычкова С. Г. Практикум по социальной статистике. 2005
8. Теория статистики: Учебник. / Под
ред. Р.А. Шмойловой. - М.: Финансы и
статистика, 2002.
9. Назаров М. Г.
Курс социально-экономической статистики. 2003
10. Палий И.А.
Прикладная статистика. 2007
11. Курс социально-экономической
статистики: Учебник для вузов / Под ред. Проф. М.Г.
12. Практикум по социальной статистике:
Учеб.пособие/ Под ред. И.И.Елисеевой.-М.: Финансы и статистика, 2002.
13. Экономическая статистика: Учебник /
Под ред. Ю.Н. Иванова. - М.: ИНФРА-М, 2002.
14. Кибанов А.Я.
«Экономика и социология труда: Учебник». – М.: ИНФРА-М, 2003. – 584с.
15. Липсиц И.В.
«Экономика: учебник для вузов». – М.: Омега-Л, 2006. – 656с. – (Высшее
экономическое образование).
16. Октябрьский П.Я. «Статистика: Учебник». – М.: ТК Велби, Изд-во Проспект, 2005.-328с.
17. Остапенко Ю.М. «Экономика
труда: Учеб. пособие». – М.: ИНФРА-М, 2006 – 268с. – (Высшее образование).
[1] При повторном отборе
вероятность попадания в выборочную совокупность всех единиц генеральной
совокупности остается одинаковой. При бесповторном - для оставшихся единиц
совокупности вероятность попадания в выборку увеличивается
[2] При
достаточно большой совокупности этот способ отбора близок к собственно
случайному, при условии, что применяемый список не составлен таким образом,
чтобы какие-то единицы совокупности имели больше шансов попасть в выборку.
[3] Здесь методика анализа
выборочного наблюдения случайных явлений не приводится, ввиду сложности
математического аппарата.
[4] на рисунке изображены штрих-линиями