ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
Контрольная работа
по дисциплине «Финансовая математика»
вариант № 4
Исполнитель:
Руководитель:
Новороссийск 2008 г.
Задание № 1.
Приведены
поквартальные данные о кредитах от коммерческого банка на жилищное
строительство (в условных единицах) за 4 года (всего 16 кварталов).
Требуется:
1) Построить адаптивную
мультипликативную модель Хольта-Уинтерса с учётом сезонного фактора, приняв
параметры сглаживания α1 = 0,3; α2 = 0,6;
α3 = 0,3.
2) Оценить точность построенной
модели с использованием средней относительной ошибки аппроксимации.
3) Оценить адекватность построенной
модели на основе исследования:
- случайности остаточной компоненты
по критерию пиков;
- независимостей уровней
ряда остатков по d-критерию (критические значения d1 = 1,10 и d2 = 1,37) и по первому коэффициенту
автокорреляции при критическом значении r1 = 0,32;
- нормальности
распределения остаточной компоненты по R/S критерию с критическими значениями
от 3
до 4,21.
4) Построить точечный прогноз на 4
шага вперед, т.е. на 1 год.
5) Отразить на графике фактические,
расчётные и прогнозные данные.
Решение:
Нам даны данные о кредитах от
коммерческого банка на жилищное строительство ( в условных единицах) за 4 года
( всего 16 кварталов).
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
|
33
|
42
|
50
|
33
|
36
|
46
|
56
|
34
|
39
|
50
|
59
|
37
|
44
|
54
|
65
|
40
|
|
1. Построим адаптивную
мультипликативную модель Хольта-Уинтерса с учётом сезонного фактора, приняв
параметры сглаживания
α1 = 0,3; α2 = 0,6; α3 = 0,3.
Для оценки начальных значений а (0)
и b (0) применим линейную модель к первым 8 значениям Y( t ). Линейная модель имеет вид:
Yр ( t ) = a ( 0 ) + b( 0 ) • t
Метод наименьших квадратов даёт
возможность определить коэффициенты линейного уравнения a (0) и b (0)
по формулам:
|
|
|
N
|
|
|
N
|
|
Ycp =
|
1
|
•Σ Y(t)
|
tcp =
|
1
|
•Σ N
|
|
|
N
|
N
|
|
|
|
|
1
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b(0) = =
|
Σ [Y(t) -
Yср] • [t - tср]
|
|
|
Σ(t - t ср.)2
|
|
|
|
|
|
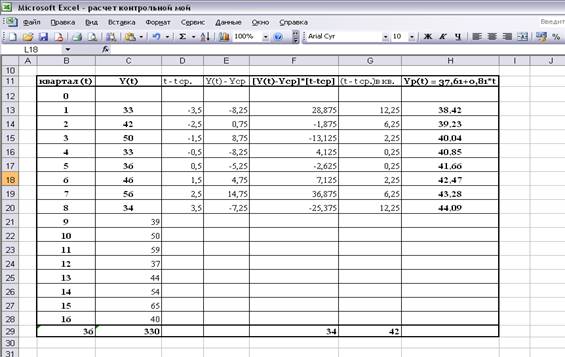
1) Ycp =
( 33 + 42 + 50 + 33 + 36 + 46 + 56 + 34 ) / 8 = 41, 25
2) t cp =
( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 ) / 8 = 4, 5
3) b (0) = 34 / 42 = 0, 81
4) a (0) = 41, 25 – 0, 81 • 4, 5 = 37,
61
Принимая во внимание найденные
значения коэффициентов, линейное уравнение принимает вид: Yр ( t ) = 37, 61 + 0, 81 • t
Из этого уравнения находим расчётные
значения Yр(t) [ для t = от 1 до 8 ] и сопоставляем их с фактическими
значениями Y(t).
Коэффициент сезонности есть отношение
фактического значения экономического показателя к значению, рассчитанному по
линейной модели.
Поэтому в качестве коэффициента
сезонности 1 квартала F(-3) может служить отношение
фактических и расчетных значений Y(t) 1-го квартала первого года,
равное Y(1) / Yр(1), и такое же отношение для 1-го квартала второго
года ( т.е. T=5) Y(5) / Yр(5). Для более точной
оценки используем среднее арифметическое значение этих двух величин:
F(-3) = [Y(1) / Yр(1) + Y(5) /
Yр(5)] /
2 = [ 33 / 38, 42 + 36 / 41, 66 ] / 2 = 0, 8615
Аналогично находим оценки
коэффициентов сезонности для 2,3 и 4 кварталов:
F(-2) = [Y(2) / Yр(2) + Y(6) /
Yр(6)] /
2 = [ 42 / 39,23 + 46 / 42,47 ] / 2 = 1, 0769
F(-1) = [Y(3) / Yр(3) + Y(7) /
Yр(7)] /
2 = [ 50 / 40,04 + 56 / 43,28 ] / 2 = 1, 2713
F(0) = [Y(4) / Yр(4) + Y(8) /
Yр(8)] /
2 = [ 33 / 40,85 + 34 / 44,09 ] / 2 = 0, 7895
Оценив значение a(0) и b(0),
а также F(-3), F(-2), F(-1) и F(0), перейдём к построению
адаптивной мультипликативной модели Хольта-Уинтерса:
Наилучшими параметрами сглаживания
являются 0,3 ; 0,6 ; 0,3 .
Из уравнения Yр (t + k) = [ a (t) + k • b (t)]
• F (t+k-L),
где k - период упреждения = 1
L - период сезонности - для
квартальных данных L = 4
t принимаем = 0, тогда Yр(1)
:
Yр ( 0 + 1 ) = Yр (1) = [ a (0) + 1 • b (0)] • F(0 + 1- 4) = [ a (0) + 1 • b (0) ] • F(-3) =
=
[ 37, 61 + 1 • 0, 81 ] • 0, 8615 = 33, 1
принимая t = 1, находим:
где а 1
= 0, 3 а (1) = a 1 • Y(1) / F (-3) + (1 – a 1) • [ a (0) + b (0) ] =
= 0,3 • 33 / 0, 8615 + (1 - 0,3) • [ 37, 61 +
0, 81 ] = 11, 49 + 0, 7 • 38, 42 = 38,
38
где а 3 = 0, 3 b (1) = a 3 • [ a (1) – a (0) ] + (1
– a 3) • b (0) =
=
0,3 • [ 38, 38 - 37, 61 ] + ( 1 - 0,3 ) • 0, 81 = 0, 231 + 0, 567 = 0, 798
где а2 = 0,6 F (1) = a 2 • Y(1) / a (1) + (1 – a
2) • F(-3) =
= 0,6 • 33 / 38, 38 + ( 1 - 0,6 ) •
0, 8615 = 0, 516 + 0, 3446 = 0, 8606
Дальнейшие расчёты проводим
аналогично, для удобства составим таблицу:
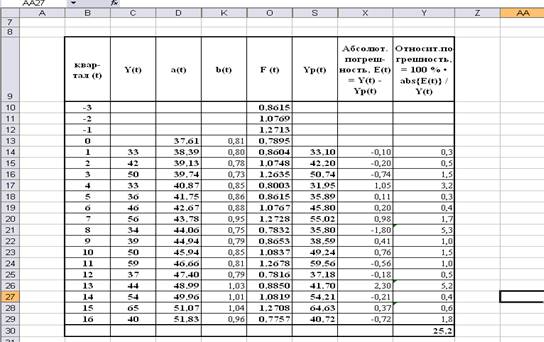
Среднее значение погрешности равно 25,2
/ 16 = 1,56 % . Следовательно, условие точности выполнено.
2.
Оценим адекватность построенной модели на основе исследования.
Для того чтобы модель была адекватна
исследуемому процессу ряд остатков E( t ) должен обладать свойствами
случайности, независимости последовательных уровней, нормальности
распределения.
Промежуточные расчёты для оценки
адекватности модели:
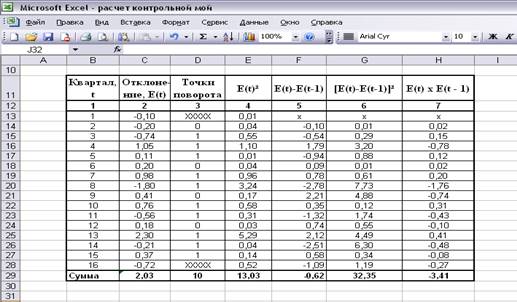
Общее число поворотных точек равно p =
10.
Рассчитаем значение q
по формуле: q = int [2(N - 2) / 3 - 2 √(16N - 29) / 90]
Функция int означает, что от
получившегося значения берется только целая часть.
При N = 16:
q
= int [ 2(16 - 2) / 3 – 2 √(16*16 - 29) / 90 ] = int [ 9,33 - 3,18 ] = int
[ 6,16 ] = 6
Так как количество поворотных точек p больше q, т.е. 10 больше 6, то условие
случайности уровней ряда остатков выполнено.
Проверка независимости уровней ряда
остатков (отсутствия автокорреляции) проводится двумя методами:
1) по d-критерию Дарбина-Уотсона:
|
d =
|
∑
[E( t ) - E (t - 1)]²
|
|
|
∑
E( t )²
|
|
|
|
|
|
d = 32, 35 / 13, 03 = 2, 48
т.к. вычисленное значение d
больше 2-х, значит, имеет место отрицательная автокорреляция и
величину d необходимо уточнить:
dуточн. = 4 – d =
4 - 2, 48 = 1, 52
если d 2 < d <
2, то уровни ряда
остатков являются независимыми:
при d 2 = 1, 37 : 1, 37 < 1, 52 < 2 при d1 = 1,10 :
следовательно,
уровни ряда E( t ) независимы.
![Надпись: R (1) = ∑ [E ( t ) • E( t – 1 )]
∑ E( t )²](ref-3898.files/image007.gif) 2)
2)
r (1) = - 3, 41 / 13, 03 = - 0, 26
Сравним модуль расcчитанного значения |r(1)|
с табличным r табл = 0, 32.
0,26 < 0,32 ; значит уровни независимы.
Проверка соответствия ряда остатков
нормальному распределению проводится по RS-критерию. Расcчитаем значение RS по формуле:
RS = ( E max – E min ) / S,
где, E max - максимальное
значение уровней ряда остатков E(t);
E min - минимальное значение уровней ряда
остатков Е(t);
S - среднее квадратическое отклонение.
2, 30 - E max - 1, 80 - E min
Emax
- Emin = 2, 30 - ( -1, 80 ) = 4, 10
S = √∑ E( t )² / (N -
1) = √ 13, 03 / 15 = √ 0, 8687 = 0, 932
RS = 4, 10 / 0, 932 = 4, 40
т.к.
критические значения не попадают в интервал от 3-х до 4, 21 -
такое исследование не проводим.
3. Составим прогноз на
четыре квартала вперед (т.е. на 1 год, с t
= 17 по t = 20).
Максимальное значение t,
для которого могут быть рассчитаны коэффициенты a ( t ), b ( t )
определяется количеством исходных данных и равно 16. Рассчитав значения a
(16) и b (16) можно определить прогнозные значения экономического
показателя Yр ( t ), для t =
17 по формуле:
Yр (t + k) = [a
( t ) + k • b( t ) ] √ F ( t + k – L )
Yр (17) = Yр(16 +1) =
[a(16) + 1 • b(16)] • F(16+1 - 4) = [a(16) + 1 • b(16)] • F(13) = [ 51, 83 + 1 • 0,9 6] • 0, 885 = 46, 71
аналогично рассчитываются Yр
(18), Yр (19), Yр (20) :
Yр (18) = Yр (16 +2) = [
a(16) + 2 • b(16)] • F(16+2 - 4) = [ a(16) + 2 • b(16)] •
•
F(14) = [ 51, 83 + 2 • 0, 96 ] • 1, 0819
= 58, 14
Yр (19) = Yр (16 +3) = [
a(16) + 3 • b(16 )] • F(16+3 - 4) = [ a(16) + 3 • b(16)]• •F(15) = [ 51, 83 + 3
• 0, 96 ] • 1, 2708 = 69, 51
Yр (20) = Yр(16 +4) = [
a(16) + 4 • b(16) ] • F(16+4 - 4) = [ a(16) + 4 • b(16) ] •
• F(16)
= [ 51,83 + 4 • 0, 96] • 0, 7757 = 43, 17
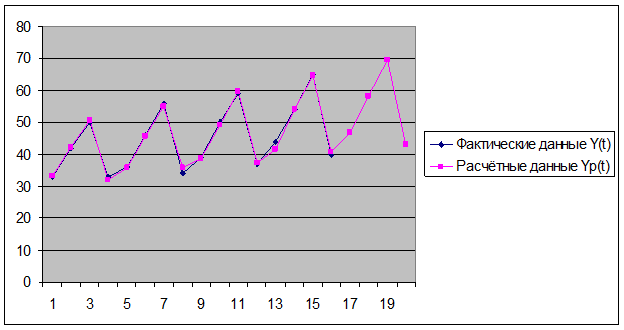
На нижеприведённом рисунке проводится сопоставление
фактических и расчётных данных. Здесь же показаны прогнозные значения о
кредитах от коммерческого банка на жилищное строительство (в условных единицах)
на 1 год вперёд. Из рисунка видно, что расчётные данные хорошо согласуются с
фактическими, что говорит об удовлетворительном качестве прогноза.
Задание № 2.
Даны цены (открытия, максимальная,
минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти
дням. Рассчитать:
- экспоненциальную скользящую среднюю;
- момент;
- скорость изменения цен;
- индекс относительной силы;
- %R, %K, и %D.
Расчёты проводить для всех дней, для
которых эти расчёты можно выполнить на основании имеющихся данных.
|
Дни
|
Цены
|
|
макс.
|
мин.
|
закр.
|
|
1
|
744
|
705
|
709
|
|
2
|
743
|
675
|
738
|
|
3
|
750
|
700
|
735
|
|
4
|
759
|
707
|
751
|
|
5
|
770
|
740
|
755
|
|
6
|
776
|
661
|
765
|
|
7
|
756
|
715
|
720
|
|
8
|
745
|
685
|
739
|
|
9
|
758
|
725
|
740
|
|
10
|
730
|
673
|
678
|
Решение:
1.
Рассчитаем экспоненциальную
скользящую среднюю (
ЕМА )
Интервал сглаживания равен 5 дням.
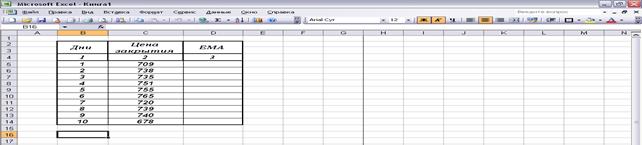
Построим таблицу и заполним графу 2
имеющимися данными по цене закрытия.
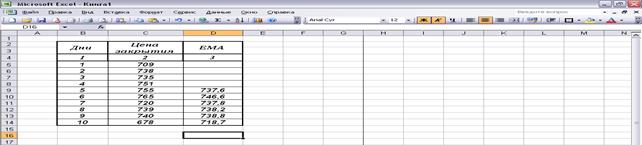
В следующей таблице приведём в графе
3 расчёты 5 – дневной ЕМА
Приведём алгоритм расчёта.
1. Выбираем интервал сглаживания n ( в нашем случае n = 5 ).
2. Вычислим коэффициент К ( К
= 2 / ( n + 1 ) = 2 / 6 = 0,33 ).
3. Вычислим ЕМА для первых 5 дней.
Для этого сложим цены закрытия за первые 5 дней. Сумму разделим на 5 и запишем
в графу 3 за 5 день.
4. Перейдём на одну строку вниз по графе
3. Умножим на К данные по конечной цене, которую берём из графы 2 текущей
строки. ( Для 6 – го дня это будет 765 • 0,33 = 252,45.)
5. Данные по ЕМА за предыдущий день
берём из предыдущей строки графы 3 и умножаем на ( 1- К ). ( Для 6 – го дня это
будет 737,6 • 0,67 = 494,19 ).
6. Сложить результаты, полученные на
предыдущих двух шагах ( для 6 – го дня это будет 252,45 + 494,19 = 746,6 ).
Полученное значение ЕМА записываем в графу 3 текущей строки.
7. Повторяем шаги 4, 5 и 6 до конца
таблицы.
Расхождение между ценой закрытия и ЕМА,
мало, чем отличаются.
2.
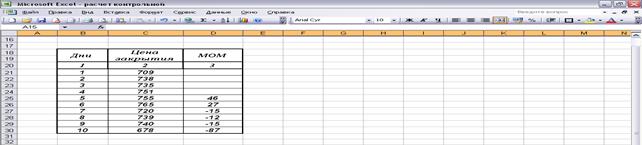
Рассчитаем момент (МОМ).
Интервал сглаживания равен 5 дням.
Момент рассчитывается, как разница
конечной цены текущего дня и цены n дней тому назад:
МОМ t = C t - C t –n.
Построим таблицу и заполним графу 2
имеющимися данными по цене закрытия, а графу 3 по формуле момента.
Построим по данным таблицы график:
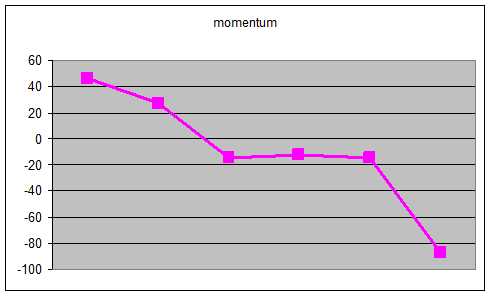
Положительные значения МОМ свидетельствуют об относительном
росте цен, отрицательные – о снижении. График момента пересекает нулевую линию
в районе 6 – 7 дней.
3.
Рассчитаем скорость изменения цен ( ROC ).
Интервал сглаживания равен 5 дням.
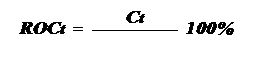 Это похожий на МОМ индикатор, который
рассчитывается, как отношение конечной цены текущего дня к цене n дней тому назад, выраженное в
процентах:
Это похожий на МОМ индикатор, который
рассчитывается, как отношение конечной цены текущего дня к цене n дней тому назад, выраженное в
процентах:
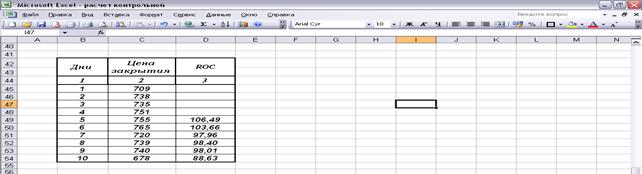
Построим таблицу и заполним графу 2
имеющимися данными по цене закрытия, а графу 3 по формуле скорости изменения
цен.
Построим по данным таблицы график:
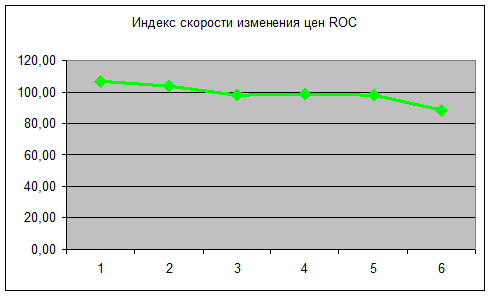
Таким образом, ROC является отражением скорости
изменения цены, а также указывает направление этого изменения. Графическое
отображение и правила работы ничем не отличаются от MOM. В качестве нулевой линии используется
уровень 100%. Этот индикатор также показал несколько запоздавший сигнал к
продаже в районе 6 – 7 дней.
4.
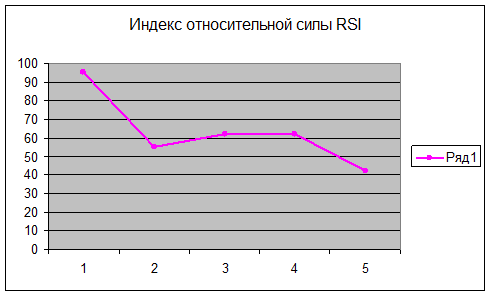
Рассчитаем индекс относительной силы ( RSI ).
Интервал сглаживания равен 5 дням.
Значение RSI изменяются от 0 до 100. Этот
индикатор может подавать сигналы либо одновременно с разворотом цен, либо с
опережением, что является его важным достоинством. Для расчёта применяют
формулу:
|
RSI = 100 -
|
100
|
|
|
|
1 + AU / AD
|
|
|
|
|
где AU – сумма приростов конечных цен за n дней; AD – сумма убыли конечных цен за n дней.
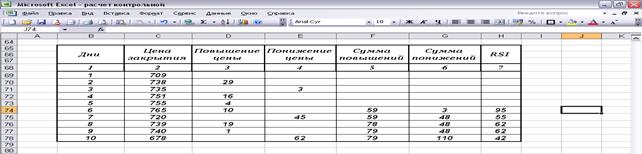
Рассчитывается RSI следующим образом.
1. Выбираем интервал n ( n =
5 ).
2. Начиная со 2-го дня до конца таблицы,
выполняем следующую процедуру. Вычитаем из конечной цены текущего дня конечную
цену предыдущего дня. Если разность больше нуля, то её записываем в графу 3.
Абсолютное значение разности записываем в графу 4.
3. С 6-го дня и до конца таблицы
заполняем графы 5 и 6. Для этого складываем значение из графы 3 за последние n дней (включая текущий) и полученную
сумму записываем в графу 5 (величина AU).
4. Аналогично находим суммы убыли
конечных цен по данным графы 4 и записываем в графу 6 (величина AD).
5. Зная AU и AD, по нашей формуле рассчитываем
значение RSI и
записываем в графу 7.
Данные наших вычислений приведены в
таблице:
Построим по данным таблицы график:
5. Рассчитаем
стохастические линии ( % R , % K , % D ).
Если MOM, ROC и RSI используют только цены закрытия, то
стохастические линии строятся с использованием более полной информации. При их
расчёте используются также максимальные и минимальные цены. Чаще всего
используют следующие кривые: % K , % D , медленная
% D и % R.
Найдём значение наших кривых по
следующим формулам:
%
Kt = 100 • ( Ct – L5 ) /
( H5 – L5 ),
%
Rt = 100 • ( H5 – Ct ) /
( H5 – L5 ).
Смысл индексов % K и % R состоит в том, что при росте цен цена
закрытия бывает ближе к максимальной, а при падении цен наоборот – ближе к
минимальной. Индексы % K и % R проверяют, куда больше тяготеет цена
закрытия. При расчёте % K разность между ценой закрытия
текущего дня и минимальной ценой за 5 дней
сравнивают с размахом цен за эти же 5 дней. В случае расчёта % R с размахом цен сравнивают разность
между максимальной ценой за 5 дней и ценой закрытия.
Индекс % D рассчитывается аналогично индексу % K, с той лишь разницей, что при его
построении величины ( Ct – L5 ) и ( H5 – C5 ) сглаживают, оперируя их трёхдневной
суммой:
|
t
|
|
|
∑ ( Сi - L 5 )
|
|
|
% Dt =
|
i=t-2
|
•
100
|
|
t
|
|
∑ ( H 5 - L 5 )
|
|
i=t-2
|
|
Ввиду того, что % D имеет большой статистический
разброс, строят ещё её трёхдневную скользящую среднюю – медленное % D.
Расчёт данных индексов приведён в
таблице:
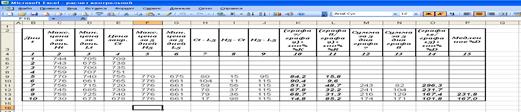
1. В графах 1 – 4 приведены дни по
порядку и соответствующие им цены (максимальная, минимальная и конечная).
2. Начиная с 5-го дня в графах 5 и 6
записываем максимальную и минимальную цены за предшествующие 5 дней, включая
текущий.
3. В графе 7 записываем ( Ct – L5 ) – разность между данными графы 4 и
графы 6.
4. Графу 8 составляют значения разности
между данными графы 5 и графы 4, т.е. результат разности ( H5 – Ct ).
5. Размах цен за 5 дней ( H5 – L5 ) – разность между данными графы 5 и
графы 6 записываем в графу 9.
6. Рассчитанные по формуле значения % K заносим в графу 10.
7. В графу 11 заносим значения % R, рассчитанные по формуле.
8. Шаги 2 – 7 повторяем до конца
таблицы.
9. Для расчёта % D, начиная с 7-й строки, складываем
значения ( Ct – L5 ) из графы 7 за 3 предыдущих дня,
включая текущий ( t = 5, 6 и 7 ), и записываем в графе 12. Аналогично значения размаха ( H5 – L5 ) из графы 9 складываем за 3
предшествующих дня и заносим в графу 13.
10.
По формуле, используя
данные граф 12 и 13, рассчитывают % D
и записывают в графе 14.
11.
Шаги 9 и 10
повторяют до конца таблицы.
12.
Медленное % D находим как скользящую среднюю от % D (данные берут из графы 14) с
интервалом сглаживания, равным трём. Результаты записываем в графе 15.
Задание № 3.
Выполнить различные коммерческие
расчёты, используя данные, приведённые в таблице. В условии задачи значения
параметров приведены в виде переменных. Например, S означает некую сумму средств в
рублях, Тлет – время в
годах, i – ставку в процентах и т.д. По именам переменных из таблицы необходимо
выбрать соответствующие численные значения параметров и выполнить расчёты.
|
Вари
ант
|
Сумма
|
Дата
начальная
|
Дата
конечная
|
Время
в
днях
|
Время
в
годах
|
Ставка
|
Число
начис
лений
|
|
|
S
|
Tн
|
Тк
|
Тдн
|
Тлет
|
i
|
m
|
|
|
4
|
2000000
|
16.01.02
|
14.03.02
|
180
|
4
|
25
|
2
|
|
Задание № 3.1.
Банк выдал ссуду, размером 2 000
000 руб. Дата выдачи ссуды – 16.01.02 г, возврата – 14.03.02
г. День выдачи и день возврата считать за 1 день. Проценты
рассчитываются по простой процентной ставке 25 % годовых. Найти:
1)
точные проценты с точным числом дней ссуды;
2)
обыкновенные проценты с точным числом дней
ссуды;
3)
обыкновенные проценты с приближённым числом дней
ссуды.
Решение:
Исходные данные:
Начальное значение PV = 2 000 000
Дата
выдачи 16.01.02
г.
Дата
возврата 14.03.02 г.
День выдачи и возврата = 1
Годовая
процентная ставка i
= 25%
Найти:
1) точные % с точным числом дней ссуды;
2) обыкновенные % с точным числом дней
ссуды;
3) обыкновенные % с приближённым числом
дней ссуды.
FV
= PV ·
( 1 + t / T · i )
1)
FV = 2 000 000 · ( 1 + 57 /
365 · 0,25 ) = 2 078 082 ,19
2)
FV = 2 000 000 · ( 1 + 57 /
360 · 0,25 ) = 2 079 166 ,67
3)
FV = 2 000 000 · ( 1 + 90 /
360 · 0,25 ) = 2 125 000
I
= FV – PV
1) I =
2 078 082, 19 – 2 000 000 = 78 082, 19
2) I =
2 079 166, 67 – 2 000 000 = 79 166, 67
3) I =
2 125 000 – 2 000 000 = 125 000
Задание № 3.2.
Через
180 дней после подписания договора должник уплатит 2 000
000 руб. Кредит выдан под 25% годовых (проценты обыкновенные).
Какова первоначальная сумма и дисконт?
Решение:
Исходные данные:
Наращенная сумма FV = 2 000 000
Количество
дней n = 180
Годовая
процентная ставка i = 25%
Найти:
Начальное значение PV
Величину
дисконта D
Поскольку срок ссуды < года, то используем формулу
простых %
PV
= FV · 1 / ( 1 + t / T · i )
PV = 2 000 000 · 1 / ( 1
+ 180 / 360 · 0,25 ) = 1 777 778
D
= FV – PV
D = 2 000 000 – 1 777 778 = 222 222
Таким образом, первоначальная сумма
долга составила 1 777 778 руб., а дисконт за 180 дней 222 222.
Задание № 3.3.
Через 180 дней предприятие
должно получить по векселю 2 000 000 руб. Банк
приобрёл этот вексель с дисконтом. Банк учёл вексель по учётной ставке 25 %
годовых (год равен 360 дням). Определить полученную предприятием сумму и
дисконт.
Решение:
Исходные данные:
Наращенная сумма FV = 2 000 000
Количество
дней n = 180
Годовая
процентная ставка = 25% (врем. база 360
дней)
Найти:
Начальное значение PV
Величину
дисконта D
D
= FV · n · d = FV · t / T ·d
D = 2 000 000 · ( 180 / 360 ) · 0,25 = 250 000
Найдём сумму, полученную предприятием
PV = FV - D
PV = 2 000 000 – 250 000 = 1 750 000
Задание № 3.4.
В кредитном договоре на сумму 2 000 000
руб. и сроком на 4 года, зафиксирована ставка сложных
процентов, равная 25 % годовых. Определить наращенную сумму.
Решение:
Исходные данные:
Начальное значение PV = 2 000 000
Срок проведения операции (лет) n
= 4 года
Номинальная процентная ставка i
= 25 %
Найти:
Наращенную сумму FV
Количество периодов начисления:
N = m · n
N = 2 · 4 = 8
Наращенная
сумма составляет:
FV = PV · ( 1 + i ) n
FV = 2 000 000 · ( 1 + 0,25 ) 4 = 4 882 812
Задание № 3.5.
Ссуда, размером 2 000 000 руб. предоставлена на 4 года. Проценты сложные, ставка
– 25 % годовых. Проценты
начисляются 2 раза в год.
Вычислить наращенную сумму.
Решение:
Исходные данные:
Начальное значение PV = 2 000 000
Срок проведения операции (лет) n
= 4 года
Номинальная процентная ставка j = 25 %
Периоды начисления m = 2
Найти:
Наращенную сумму FV
Количество периодов начисления:
N = m · n
N = 2 · 4 = 8
Наращенная
сумма составляет:
FV = PV · ( 1 + j / m ) N
FV = 2 000 000 · ( 1 + 0,25 / 2 ) 8 = 5 131 569
Задание № 3.6.
Вычислить эффективную ставку процента,
если банк начисляет проценты 2 раза
в год, исходя из номинальной ставки 25
% годовых.
Решение:
Исходные данные:
Периоды начисления m = 2
Номинальная процентная ставка j = 25 %
Найти:
Эффективную ставку i
i = ( 1 + j / m )m – 1
i = ( 1 + 0,25 / 2 )2 – 1 = 0,265625, т.е. ≈ 27 %
Задание №
3.7.
Определить, какой должна
быть номинальная ставка при начислении процентов 2 раза в год,
чтобы обеспечить эффективную ставку 25 % годовых.
Решение:
Исходные данные:
Периоды начисления m = 2
Эффективная ставка i = 25 %
Найти:
Номинальную процентную ставку j
j = m · [ ( 1 + i ) 1 / m – 1 ]
j = 2 · [ ( 1 + 0,25 ) 1 / 2 – 1 ] = 0,23607, т.е. ≈ 24 %
Задание № 3.8.
Через 4 года предприятию будет выплачена сумма 2 000 000 руб.
Определить её современную стоимость при условии, что применяется сложная
процентная ставка 25 % годовых.
Решение:
Исходные данные:
Начальное значение PV
= 2 000 000
Срок проведения операции (лет) n = 4
года
Годовая процентная ставка i = 25 %
Найти:
Современную стоимость FV
FV = PV · ( 1+ i ) n = PV · K n
FV = 2 000 000 · 0, 4096 = 819 200
Задание №
3.9.
Через 4 года
по векселю должна быть выплачена сумма 2 000 000 руб.
Банк учёл вексель по сложной учётной ставке 25 % годовых.
Определить дисконт.
Решение:
Исходные данные:
Наращенная сумма FV =
2 000 000
Срок проведения операции (лет) n = 4
года
Дисконтная величина векселя d
= 25 %
Найти:
Дисконт D
PV = FV · ( 1 – d )n
PV = 2 000 000 · ( 1 – 0,25 )4 = 632 812, 50
D = FV – PV
D = 2 000 000 – 632 812, 50 = 1 367 187, 50
Задание №
3.10.
В течение 4
лет на расчётный счёт в конце каждого года поступает по
2 000 000 руб., на которые 2 раза в год начисляются проценты по
сложной годовой ставке 25 % . Определить сумму на расчётном счёте
к концу указанного срока.
Решение:
Исходные данные:
Размер очередного платежа R = 2 000 000
Номинальная ставка j = 25 %
Срок ренты n = 4
Периоды начисления m = 2
Найти:
Наращенную сумму ренты FVA
FVA = R · [ ( 1 + j / m )mn
– 1 ] / [ ( 1 + j / m )m –
1 ]
FVA
= 2 000 000 · [ ( 1 + 0,25 / 2 ) 8 –
1 ] / [ ( 1 + 0,25 / 2 )2 –
1 ] = 11 800 000