1 Расчёт метрологических характеристик

Случайная составляющая погрешности измерения, подчиняющаяся закону нормального распределения характеризуется её среднеквадратичным значением 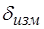. Эта погрешность складывается из методической погрешности измерительной системы (инструментальной).

Для оценки соотношения между метрологической погрешностью и погрешностью измерения, зададимся коэффициентом γ1.

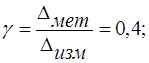
(1.1)

Методическая погрешность:

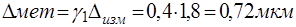
(1.2)

1.1 Расчет предельного значения основной погрешности.

Среднеквадратическое отклонение случайной составляющей погрешности измерения

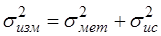
(1.3)

По закону равной вероятности среднеквадратическое отклонение методической погрешности равно:

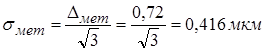
(1.4)

По закону нормального распределения среднеквадратическое отклонение погрешности измерения равно:

	(1.5)
	(1.6)

Допустимая приведённая основная погрешность системы:

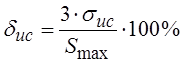
	(1.7)

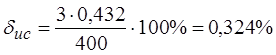
где  Smax – диапазон изменения измеряемой величины.

Полученное значение округляется до ближайшего более точного значения взятого из ряда класса точности ГОСТ 8.401-80: 4,0·10-3.

Таки образом, класс точности будет равен 0,4.

Дисперсия некоррелированной случайной погрешности по закону нормального распределения:

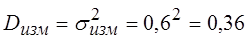
(1.8)

1.2 Выбор дополнительной погрешности.

Дополнительная погрешность – это погрешность СИ, вызванная отклонением внешних условий от нормальных, но не превышающих значений условий эксплуатации и использования.

Принимаем дополнительную погрешность, равную основной.

1.3   Расчет информационных характеристик.

Определим шаг квантования.

Случайная составляющая допустимой основной погрешности измерения (на выходе АЦП):

;

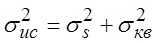(1.9)

Зададимся коэффициентом γ2=0,4;

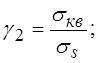
(1.10)

откуда:

	(1.11)
;	(1.12)
	(1.13)

Диапазон входной аналоговой величины в нормированном виде:

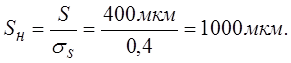
(1.14)

Шаг квантования:

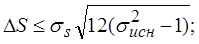
(1.15)

где:

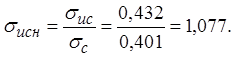
(1.16)

1.4 Определение разрядности кода

,

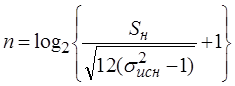(1.17)

где: n – количество разрядов кода;

Sн – Диапазон входной аналоговой величины в нормированном виде. Sн=1000 мкм;

σисн – случайная составляющая допустимой основной погрешности измерения в нормированном виде σисн=1,077.

Таким образом, принимаем разрядность кода равной 8.