Приложение 2
Теоретические основы курса «Комплексные числа»
 § 1 Развитие понятия числа, комплексные числа, алгебраическая форма, действия над комплексными
числами, заданными в алгебраической форме. Комплексная плоскость.
Геометрическая интерпретация комплексного числа, их суммы и разности.
§ 1 Развитие понятия числа, комплексные числа, алгебраическая форма, действия над комплексными
числами, заданными в алгебраической форме. Комплексная плоскость.
Геометрическая интерпретация комплексного числа, их суммы и разности.
 При изучении математики мы уже неоднократно встречались с обобщением понятия
числа. До сих пор мы рассматривали лишь действительные числа. Если введение
действительных чисел позволяет выражать результаты любых измерений, то с
задачей решения уравнений дело обстоит иначе. Например, уравнения
При изучении математики мы уже неоднократно встречались с обобщением понятия
числа. До сих пор мы рассматривали лишь действительные числа. Если введение
действительных чисел позволяет выражать результаты любых измерений, то с
задачей решения уравнений дело обстоит иначе. Например, уравнения  х2 + 1=0 и х2 +4х +5=0 не имеют решения
во множестве действительных чисел, хотя коэффициенты этих уравнений – целые
числа. Поэтому возникает необходимость в дальнейшем расширении понятия числа.
Таким обобщением множества действительных чисел и является множество С
комплексных чисел.
х2 + 1=0 и х2 +4х +5=0 не имеют решения
во множестве действительных чисел, хотя коэффициенты этих уравнений – целые
числа. Поэтому возникает необходимость в дальнейшем расширении понятия числа.
Таким обобщением множества действительных чисел и является множество С
комплексных чисел.
Комплексные
числа часто называют мнимыми. Это название не вполне удачно, т.к. может создать
представление о комплексных числах как о чём-то нереальном. Оно объясняется
тем, что, хотя комплексные числа стали употребляться ещё в XVI в., они долго продолжали казаться
даже выдающимся математикам чем-то реально не существующим, мнимыми в
буквальном смысле этого слова. Одному из создателей дифференциального и
интегрального исчисления, немецкому математику Г.Лейбницу (1646-1716) принадлежат,
например, такие слова: „Комплексное число – это тонкое и поразительное средство
божественного духа, почти амфибия между бытием и небытием”. Сейчас от всей этой
мистики не осталось ничего, кроме, пожалуй, названия «мнимые числа». Уже во
времена К.Гаусса (1777-1855) было дано геометрическое истолкование комплексных
чисел как точек плоскости. Трудами выдающихся математиков XIX века О.Коши, Г.Римана и К.Вейерштрасса
на базе комплексных чисел была построена одна из самых красивых математических
дисциплин – теория функций комплексной переменной.
Повторить с
учащимися известные им сведения о числовых множествах:
а) натуральных
чисел N={1,2,3,…,n,…};
б) целых Z={…,-2,-1,0,1,2,…};
в) рациональных Q={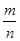 ,n
,n 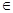 Z, n
Z, n 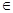 N};
N};
г) действительных чисел R.
С помощью положительных
действительных чисел можно выразить результат любого измерения, а с помощью
произвольных действительных чисел – изменение любой величины. Арифметические
операции над действительными числами снова дают действительные числа. Операция
же извлечения квадратного корня определена не для всех действительных чисел, а
лишь для неотрицательных – из отрицательного числа квадратный корень извлечь
нельзя.
Ряд вопросов, возникших при решении
уравнений третьей и четвертой степеней, привел математиков к необходимости
расширить множество действительных чисел, присоединив к ним новое число i, такое, что i2=-1.Поскольку действительных чисел с таким свойством
не существует, новое число назвали “мнимой единицей” – она не выражала ни
результатов измерения величин, ни изменений этих величин. Но включение числа i потребовало дальнейшего расширения
множества чисел – пришлось ввести произведение этого числа на все
действительные числа, т.е. числа вида bi, где b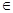 R, а также суммы действительных чисел и таких
произведений, т.е. числа вида a+bi, где a,b
R, а также суммы действительных чисел и таких
произведений, т.е. числа вида a+bi, где a,b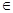 R. Получившиеся при этом числа были названы
комплексными, т.к. они содержали как действительную часть a, так и чисто мнимую часть bi.
R. Получившиеся при этом числа были названы
комплексными, т.к. они содержали как действительную часть a, так и чисто мнимую часть bi.
Опр: комплексными числами
называются числа вида a+bi (a и b - действительные числа, i2=-1).
Если z=а+bi - комплексное число, то а называют
его действительной частью, а b-мнимой частью. Приняты обозначения a=Re z, b=Jm z (от французских слов re¢ele - действительный и imaginaire - мнимый). Числа a+bi, для которых b¹0,
называют мнимыми числами, а числа вида bi, b¹0,- чисто мнимыми числами.
Множество
комплексных чисел обозначается С.
Два комплексных
числа z1=a+bi
и z2=с+di считаются равными
друг другу в том и только в том случае,
если а=с и b=d. В частности, число a+bi будет считать равными нулю, если a=0 и b=0.
Запись z=a+bi называется алгебраической формой
комплексного числа.
Действия
над комплексными числами:
1. Сложение: (a+bi)+(c+di)=(a+c)+(b+d)i
Например , (2+3i)+(5-7i)=(2+5)+(3-7)i=7-4i.
2.
Умножение: (a+bi)*(c+di)=(ac-bd)+(ad+bc)i ,
причем нужно помнить, что i2 =-1. Эту формулу
можно получить, умножая
(a+bi) на (c+di) по правилам действий над
многочленами.
Например, (1+2i)(3-i) =3*1-1*i+6i-2i2 =3+2-i+6i=5+5i.
Рассмотрим
степени числа i :
i1 =i ; i2 =-1; i3 =i2*i =-1*i
=-i; i4 =i2*i2
=(-1)(-1) =1; i5=i3*i2=-i(-1)=i; i6= =i5*i=i*i=-1=i2;
…
Вообщее, i4n+r =(i4)n*ir
=(1)n *ir =ir.
Получаем, i4m=1; i4m+1=i; i4m+2=-1; i4m+3=-i.
Например, i218=i4*54+2=i2=-1.
3. Вычитание: (a+bi) - (c+di) = (a-c) + (b-d)i
Например, (5+4i) - (2-3i) = (5-2) + (4+3)i = 3+7i.
Опр: Два комплексных
числа называются сопряженными, если они отличаются лишь знаком мнимой части.
Если z=a+bi, то сопряженное число имеет вид z=a-bi. Заметим, что z+z=(a+bi)+(a-bi)=2a; z*z=(a+bi)(a-bi)=a2+b2 . Следовательно, сумма и произведение двух сопряженных комплексных
чисел являются действительными числами.
4. Деление:
на практике при делении комплексных чисел удобно домножить числитель и
знаменатель дроби на выражение, сопряженное знаменателю:
a+bi = (a+bi)(c-di) = (ac+bd)+(bc-ad)i
= ac+bd + bc-ad i
c+di (c-di)(c-di) c2 + d2 c2+d2 c2+d2
Например, 10+15i
= (10+15i)(1-2i) _ 10-20i
+15i +30 = 40-5i = 8-i
1+2i (1+2i)(1-2i) 1 + 4 5
Геометрическая интерпретация
комплексных чисел.
Как известно,
действительные числа можно изображать точками на координатной прямой. А
комплексное число естественно выражать точкой на координатной плоскости.
Каждому
комплексному числу a+bi поставим в соответствии точку M(a;b) координатной плоскости, т.е. точку, абсцисса которой равна
действительной части комплексного числа, а ордината - мнимой части. Каждой
точке M(a; b)
координатной плоскости поставим в соответствие комплексное число a+bi (рис.1).
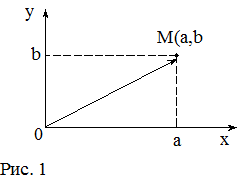
Очевидно, что
получаемое при этом соответствие является взаимно однозначным. Сама
координатная плоскость называется
комплексной плоскостью. Действительным числам соответствуют точки оси
абсцисс, которая называется действительной осью, а чисто мнимым числам - точки
оси ординат, которая называется мнимой осью.
Не менее важной
и удобной является интерпретация комплексного числа a+bi как радиус-вектора ОМ (см. рис.1), т.е. вектора, исходящего из
начала координат О (о,о) и идущего в точку М (а;b). Разумеется, вместо радиус-вектора ОМ
можно взять любой равный ему вектор.
Изображение
комплексных чисел с помощью векторов удобно тем, что при этом получают простое
геометрическое истолкование операций над ними. При сложении чисел z1=a1+b1i и z2=a2+b2i складываются их действительные и
мнимые части. При сложении соответствующих им векторов ОМ1 и ОМ2
складываются их координаты. Иными словами, если числу z1 соответствует вектор ОМ1,
а числу z1-вектор
ОМ2, то числу z1+z2 соответствует
вектор ОМ1+ОМ2, а числу z1-z2 - вектор ОМ1-
ОМ2.
Перейдем к
рассмотрению понятия модуля комплексного числа. Опр: Модулем комплексного числа
называется длина вектора соответствующего этому числу.
Для модуля
числа z используется
обозначение /Z/ или r. По теореме Пифагора (см.
рис.1) для модуля комплексного числа z=a+bi легко получается следующая
важная формула: /Z/=Öa2+b2, выражающая модуль
числа через его действительную и мнимую части. Отмети, что /z/ = /-z/ = /z/, z*z = /z/2 = /z/2.
Упражнения:
1. (2Ö3 - 4iÖ2) - (Ö27 - iÖ32) + (2
+ 2i
Ö3
Ö3
;
2. (m -
n i) + ( n - m i - (( 1
- 1 i) - 1 - 1 i))
;
n m
m n n
m m n
3. 2i (1 + Ö3 i) ( -1
+ Ö3 i );
2 2
2 2
4. Найдите комплексные числа:
а) z =i + 6i+1 б) z = i13+ i14 + i15 +i16
; в) z = 3+1 : 2
1+7i
3-i 5(1-i)
г) z = (1+2i)3 - (1-i)3 ; д) z = (2+i)5 е) z = 5+12i + (1+2i)2
(3+2i)3- (2+i)2
8-6i 2+i
ж) z = (-0,5 + i Ö3) 3
2
5. Изобразить геометрически комплексные числа:
а) 3+0i; б) 0-5i; в) -3+2i; г) 1+i.
6. Найдите действительную часть
комплексного числа:
z= (1+2i) + i19 ;
мнимую : z= (2-i)3 (2-11i).
7. Найти модуль к.ч. z= -2+ i*5, число, сопряженное данному, изобразить
их геометрически.
8.
Выполнить сложение алгебраически и дать геометрическую
интерпретацию: z= z1 +z2
+z3,
где z1 = 3-2i; z2=-3+4i; z3 = 2- i.
9.
Найти два действительных числа Х и У, удовлет их равенствам:
а) 2i + iу -2 = 3i
- 3 =у
х х
б) (1+i)x + (1-i)у = 3-i;
в) (2x-3уi)(2x+3уi) +xi = 97+2i.
§2. Действия над комплексными числами,
заданными
в алгебраической
форме. Решение задач.
Провести
комбинированный опрос. Фронтальный опрос провести по вопросам:
1. Обозначение числовых множеств и их соотношения.
2. Почему появилась необходимость
введения комплексных чисел?
3.
Определение комплексных
чисел, частные случаи, основные соглашения.
4.
Определения сопряженных и противоположных комплексных чисел,
модуля комплексного числа.
5.
Геометрическая интерпретация комплексных чисел, сопряженных и
противоположных комплексных чисел.
6.
Действия над комплексными числами, заданными в алгебраической
форме (определения и свойства).
7.
Действия над комплексными числами, геометрическая интерпретация
их суммы и разности.
8.
Действия над сопряженными и противоположными комплексными
числами (их сумму и разность показать геометрически).
9.
Можно ли сравнивать комплексные числа?
10.
Какие закономерности имеются у степени мнимой единицы.
Индивидуальный
опрос полезно провести по карточкам. Примерное содержание одного варианта:
1. Вычислить: а) (3+5i) + (2+i) = . . . . .; б) (3+5i) - (4-i) = . . . .;
2. Возвести в степень: а) i123 = . . . ; б)
(i-1)2 = . .
. .
3. Вычислить: (Ö3 + iÖ2) (Ö3 - iÖ2) = . . . .
4.
Построить слагаемые и сумму комплексных чисел на комплексной
плоскости: z1=1-5i; z2=2+3i.
5.
Построить уменьшаемое, вычитаемое и разность комплексных чисел
на комплексной плоскости: z1=1-i; z2=3i.
Упражнения:
1. Выполнить действия: а) [2i (3-4i)]2 =; б) a-bi - i b-ai = ;
b+ai a+bi
в) i100 + i98 +i63
=;
2.
Н основании равенства комплексных чисел, найти действительные
числа Х и У, если а) 2+5i x -
3уi = 14i + 3x -5y; б) x2
-7x +9yx = y2i
+20i -12.
3. При каких действительных значениях Х и У
комплексного числа
а) 5 + ixy и x + y +4i; б) 9y2 - 4 - 10x и 8y2 + 20i7
Будут сопряженными?
4. Решите уравнения: а) (i-z) (1+2i)
+ (2-iz) (3-4i) = 1+7i;
б) z2 - (5+2i) z + 5 + 5i =0; в) z2 + z =0; г) (1-i) z - 3iz = 2-i; д) z*z + 2z =3+2i;
е) z*z + 3(z-z) - 4+3i.
5. Решите уравнения: а) /z/ = 2i (z+1); б) /z/
= i (2z+i); в) /z/
- iz = i-2i;
г) z2 + 3/z/ =0;
д) z2
+ /z/2 =0.
8. Какое множество точек комплексной плоскости
задается условием:
а) /z/ <1; б) /z/ =2; в) Rez > 1; г) Jmz < -2; д) /z+i/ =2;
е) /z-2/ <3; ж) /z-4 +i/ £5.
7. Точка А соответствует комплексному
числу z = 3+ i4. Какое комплексное число
соответствует точке симметричной точке А, относительно: а)оси Ох; б)
оси Оу; в) начала координат?
8. На комплексной плоскости даны точки
z1, z2 , z3 являющиеся вершинами некоторого треугольника.
Найдите все комплексные числа, соответствующие точками, дополняющим данный
треугольник до параллелограмма.
9. Изобразить: а)
/z/ £3 б)/z/³
1 в) /z-1/³
2
/z-3i/³3 /z-2i/£2 -1< Rez<2
г) 1£ /z-1/£
2 д) /z/ £3
0£ Jmz£Ö3 1< Jmz <2.
§
3 Тригонометрическая форма комплексного
числа.
Переход от алгебраической формы
комплексного числа к тригонометрической и обратно.
Повторить с учащимися
алгебраическую форму комплексного числа; геометрическую интерпретацию
комплексного числа; модуль комплексного числа и основные соотношения, связанные
с ним.
Пусть точка А соответствует комплексному
числу z=a+bi. Тогда длина вектора ОА называется
модулем числа z, а радианная мера угла,
образованного этим вектором с
положительным направлением действительной
оси, - аргументом комплексного числа Z. Причем величина угла
считается положительной, если отсчет ведется против часовой стрелки, и
отрицательной, если отсчет производится по часовой стрелке. Модуль обозначается
/z/ = r, а аргумент - argz = j (см. рис. 2).
Для числа z=0 аргумент не определяется, но в этом и только в этом случае
число задается только своим модулем. Если комплексное число является
действительным, то соответствующий ему вектор расположен на действительной оси,
и понятие /z/ совпадает
с известным понятием модуля действительного числа.
Заданием модуля
и аргумента комплексное число определяется однозначно. Но аргумент комплексного
числа, в отличие от модуля, определяется не однозначно. Любые два аргумента
комплексного числа отличаются друг от друга слагаемым, кратным 2p.
На рис. 2 мы
видим, что sin j = b/r, а cos j =a/r,
отсюда а=r cos j и b=r sin j, где r =Öa2 + b2, т.о.
действительная и мнимая части комплексного числа z=a+bi
выражаются через его модуль /z/=r и аргумент j.
Следовательно, комплексное число z может быть записано в виде z=r cos j + i r sin j=r(cos j+i sin j) - тригонометрическая форма
записи комплексного числа.
Полезно
составить с учащимися алгоритм перехода из алгебраической формы комплексного
числа в тригонометрическую:
1. Найти радиус r = Öa2 + b2
2. Вычислить tg j1 =|b/a|.
3. По знакам a
и b определить четверть, в которой находится число z.
4. Найти j, причем, если число
находится:
а) в I четверти, то j = j1;
б) во II четверти, то j = p - j1;
в) в III четверти, то j = p + j1;
г) в IV четверти, то j = -j1,
или j
= 2p
-j1.
5. Записать комплексное число в тригонометрической
форме:
z = r (cos j + i sin j).
Или, чтобы не
производить лишних вычислений, для того чтобы найти значение для j по
известным значениям sin j и cos j, заполним таблицу и будем ею
пользоваться:
|
j
|
0
|
p
6
|
p
4
|
p
3
|
p
2
|
p
|
5p
6
|
3p
4
|
2p
3
|
3p
2
|
4p
3
|
4p
4
|
7p
6
|
5p
3
|
7p
4
|
11p
6
|
2p
|
|
sinj
|
0
|
1
2
|
Ö2
2
|
Ö3
2
|
1
|
0
|
1
2
|
Ö2
2
|
Ö3
2
|
-1
|
-Ö3
2
|
-Ö2
2
|
-1
2
|
-Ö3
2
|
-Ö2
2
|
-1
2
|
0
|
|
cosj
|
1
|
Ö3
2
|
Ö2
2
|
1
2
|
0
|
-1
|
-Ö3
2
|
-Ö2
2
|
- 1
2
|
0
|
-1
2
|
-Ö2
2
|
-Ö3
2
|
1
2
|
Ö2
2
|
Ö3
2
|
1
|
Переход от
тригонометрической формы комплексного числа к алгебраической производится
подстановкой в выражение z=r (cos j + i sin j) числовых значений cos j
и sin j,
затем раскрываются скобки и производятся
упрощения.
Например: 1) z = 1+i
/z/ r =Ö
12+12 =Ö2
sinj = 1 =2 cosj = 1
= 2 Þj = 450
Ö2
2 Ö2 2
т.о z = a + bi = 1 + i = Ö2 (cos 450+ isin 450
=Ö2 (cos p + sin p)
4 4
2. z = 6( cosp + isin p) = 6 (-1 + i*0) = 6*-1 = -6 Þz = -6.
Упражнения:
1. Представьте в тригонометрической
форме комплексные числа:
а) Ö3-i ; б) 6+6i ; в) -2 ; г) i ; д) -1 - Ö3 i
е) -3 (cos p + isin p
2 2 ; 7 7
;
ж) sin 48° + cos 48° ;
з) 1 + cos 10p + isin 10p
9 9
2. Представьте в алгебраической форме комплексные
числа :
а) z = 2 (cos 225° + isin 225°) ; б) z=3 (cos0° + isin 0°) ;
в) z = 5(cos p + isin p
; г) z = 2(cos p + isin p
2 2 3 3
3. Построить
комплексные числа? А) z=2 (cos
p + isin p )
4 4
б) z = cosp + isin p ; в) z =2 (cos 3p + isin 3p
4 4