III. Методы аппроксимации
3.1 Приближение функций многочленами.
Алгебраическим многочленом степени n называется функция 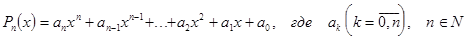 - действительные числа, называемые коэффициентами.
- действительные числа, называемые коэффициентами.
Алгебраические многочлены являются простейшими функциями. Они
непрерывны при любом x. Производная
многочлена- так же многочлен, степень которого на единицу меньше степени
исходного. Так, если степень n,
то 
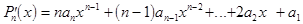 .
.
В школьном курсе математики рассматриваются функции f(x)=ax, f(x)=logax,
f(x)=sin(x) и др., изучаются их свойства, строятся графики. Однако
вопрос о методах вычисления значений названных функций при заданных значениях
аргумента не рассматривается. Вместе с тем, он очень важен. Познакомимся с
методами приближения функций, или методами аппроксимации.
3.2 Формула Тейлора.
Рассмотрим функцию y=f(x),
определённой на некотором промежутке, содержащим т.а. Предположим, что
эта функция имеет производные (n+1)-го
порядка. 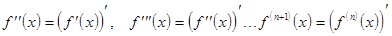
Уравнение касательной к графику функции в т. х=а имеет вид: 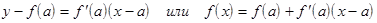 .
.
Многочлен 1-й степени: 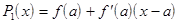 в т. х=а совпадает со
значением f(x) в этой
точке: P1(a)=f(a).
Многочлен в т. х=а имеет то же значение производной, что и функция.
Действительно, P1’(x)=f’(a),
следовательно, P1’(а)=f’(a). График многочлена Р1(х)
касается графика функции y=f(x)
в т. М0(а,f’(a)).
в т. х=а совпадает со
значением f(x) в этой
точке: P1(a)=f(a).
Многочлен в т. х=а имеет то же значение производной, что и функция.
Действительно, P1’(x)=f’(a),
следовательно, P1’(а)=f’(a). График многочлена Р1(х)
касается графика функции y=f(x)
в т. М0(а,f’(a)).
Можно найти многочлен 2-й степени, а именно: 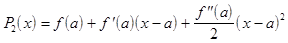 , который в т. х=а будет иметь с функцией y=f(x) общее значение и одинаковые
значения как первых, так и вторых производных. График многочлена Р2(х)
вблизи т. х=а ещё теснее будет прилегать к графику функции y=f(x) по сравнению с графиком
многочлена Р1(х).
, который в т. х=а будет иметь с функцией y=f(x) общее значение и одинаковые
значения как первых, так и вторых производных. График многочлена Р2(х)
вблизи т. х=а ещё теснее будет прилегать к графику функции y=f(x) по сравнению с графиком
многочлена Р1(х).
Естественно ожидать, что многочлен, имеющий при х=а первые n производных, одинаковых с
соответствующими производными функции f(x) в той же точке, при х, близких к а, будет хорошо приближать f(x). В этом случае вместо f(x) можно рассматривать
указанный многочлен, а для приближённого вычисления f(x) при заданном х достаточно вычислить
его значения при том же х.
Этот многочлен получают в результате решения следующей задачи: для
функции f(x), имеющей в
окрестности т. х=а производные до порядка n+1 включительно, найти многочлен Рn(x) степени не выше n такой, что Pn(a)=f(a); Pn’(a)=f’(a); Pn’’(a)=f’’(a);... Pn(n)(a)=f(n)(a).
Эти равенства означают, что в т. х=а значения многочлена Рn(x) и функции y=f(x), а так же их соответствующих
производных совпадают. Многочлен Pn(x) представим в виде: 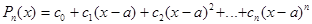 . Коэффициенты
. Коэффициенты 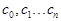 определяются,
предварительно найдя его производные:
определяются,
предварительно найдя его производные:
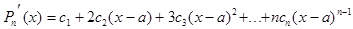
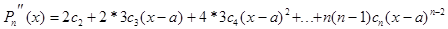
......................................
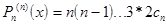
Подставляя в формулы значения х=а, получим:
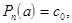
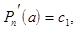

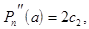 ...
...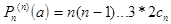
Из этих равенств находим, что
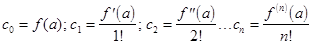

Получаем искомый многочлен:
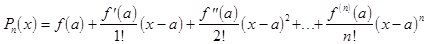 .
.
Обозначим через rn(x)
разность между функцией f(x)
и многочленом Pn(x).
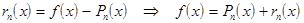
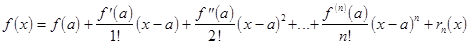
Величину rn(x)
называет остаточным членом. Видно, что при тех же значениях х,
для которых rn(x)
достаточно мал, вместо f(x)
можно рассматривать многочлен Pn(x).
Оценим величину остаточного члена rn(x). Запишем его в виде 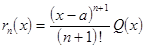 , где Q(x)- функция, которую нужно
определить. Формула примет вид:
, где Q(x)- функция, которую нужно
определить. Формула примет вид: 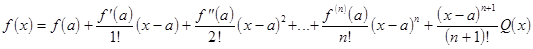
При фиксированных значениях а и х функция Q(x) имеет определённые значения,
которые обозначаются через Q.
Рассмотрим вспомогательную функцию переменной t (a<t<x)
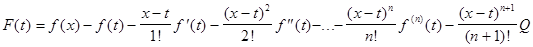 Применяя
правила дифференцирования алгебраической суммы и произведения двух функций,
находим производную функции F(t)
по аргументу t.(x и а- фиксированные,
следовательно, f(x)-
постоянная).
Применяя
правила дифференцирования алгебраической суммы и произведения двух функций,
находим производную функции F(t)
по аргументу t.(x и а- фиксированные,
следовательно, f(x)-
постоянная).
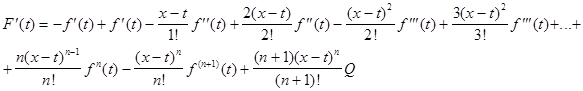
 Приведя подобные слагаемые, получим:
Приведя подобные слагаемые, получим:
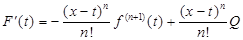
Из формулы функции F(t)
видно, что F(x)=0 и F(a)=0. Воспользуемся
свойством дифференцируемой функции:
Если дифференцируемая функция f(x) обращается в нуль при х=а и х=b, f(a)=0, f(b)=0, (a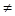 b), то между точками а и b найдётся по крайней мере одна т.с, в
которой равна нулю производная данной функции: f’(c )=0. (т. Ролля).
b), то между точками а и b найдётся по крайней мере одна т.с, в
которой равна нулю производная данной функции: f’(c )=0. (т. Ролля).
Геометрически это означает, если в т. а и b f(a)=0 и f(b)=0, то 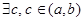
 такое, что в т. С(с,f(c )) касательная к графику y=f(x) параллельна оси ОХ.
такое, что в т. С(с,f(c )) касательная к графику y=f(x) параллельна оси ОХ.
 y
y
f©
0 a c b X
Корнем или нулём функции называют такое значение аргумента х0
, при котором функция f(x0)=0.
С учётом этого понятия указанное свойство можно сформулировать так:
между двумя различными корнями дифференцируемой функции находится хотя бы один
корень её производной (т. Ролля).
Поскольку F(x)=0
и F(a)=0, то к функции F(t) можно применить свойство: 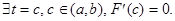
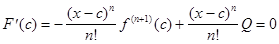
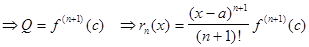
Так как с заключено между а и х, то его можно представить в виде 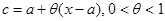
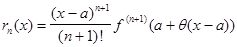
Говорят, что это равенство выражает остаточный член формулы в форме
Лагранжа. Подставим его в формулу:
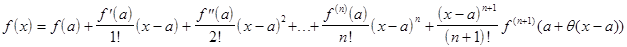 Эту формулу называют формулой Тейлора с остаточным членом в
форме Лагранжа.
Эту формулу называют формулой Тейлора с остаточным членом в
форме Лагранжа.
Если а=0, то 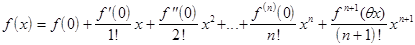
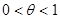
Формула Тейлора для функций sinx, cosx, ex
Выведем формулы Тейлора для элементарных функций f(x)=sinx, f(x)=cosx, f(x)=ex.
Рассмотрим функцию f(x)=sinx.
Найдём производную n+1-
го порядка.
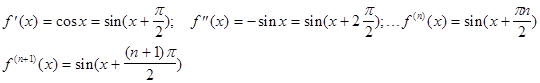 Вычислим значение функции и её
производной при х=0.
Вычислим значение функции и её
производной при х=0.
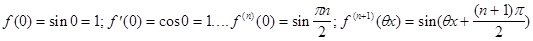 Подставим эти значения в формулу
Тейлора:
Подставим эти значения в формулу
Тейлора:
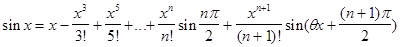
2.Аналогично находим формулу Тейлора для f(x)=cosx. 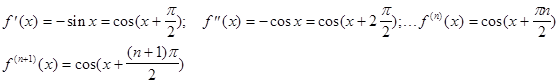

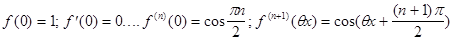
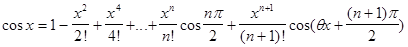
3.Рассмотрим функцию f(x)=ex.
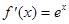 ,
, 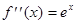 ...
...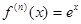
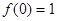 ,
, 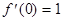 ...
...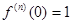 ,
, 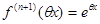
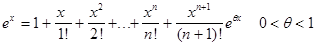
4.Рассмотрим
функцию f(x)=(a+x)n
, 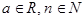
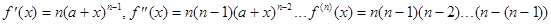


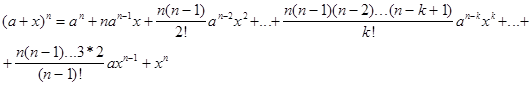
Эту формулу называют биномом Ньютона. Отметим частные случаи:
n=2 (a+x)2=a2+2ax+x2
n=3 (a+x)3=a3+3a2x+3ax2+x3
Приближение функций sinx, cosx, ex
алгебраическими многочленами.
В формуле Тейлора для sinx положим n=2m-1
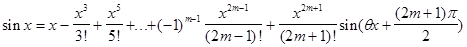
Остаточный член этой формулы имеет вид:
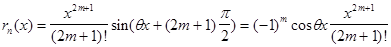
Оценим его модуль. Поскольку  Отбрасывая остаточный член, получим приближённо:
Отбрасывая остаточный член, получим приближённо:
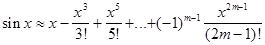 . Она может быть применена для вычисления значений функции f(x)=sinx при заданных
значениях аргумента х. Эти вычисления сводятся к вычислениям значений
алгебраического многочлена степени 2m-1
. Она может быть применена для вычисления значений функции f(x)=sinx при заданных
значениях аргумента х. Эти вычисления сводятся к вычислениям значений
алгебраического многочлена степени 2m-1 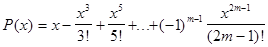 . Следовательно, вместо функции f(x)=sinx можно рассматривать
алгебраический многочлен, который приближённо заменяет её. Говорят, что
указанный многочлен приближает данную функцию. Оценка такого приближения
определяется формулой:
. Следовательно, вместо функции f(x)=sinx можно рассматривать
алгебраический многочлен, который приближённо заменяет её. Говорят, что
указанный многочлен приближает данную функцию. Оценка такого приближения
определяется формулой: 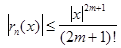
Полагая n=2m
в формуле для cosx, аналогично: 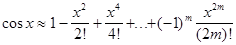 , погрешность
, погрешность 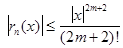 .
.
Например, для приближённой формулы 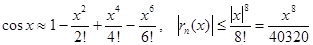
В случае функции f(x)=ex,
получаем: 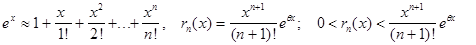
В общем случае, отбросив остаточный член, получим приближённую
формулу: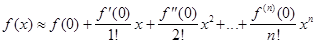 . Она позволяет заменить данную функцию алгебраическим
многочленом n-й
степени:
. Она позволяет заменить данную функцию алгебраическим
многочленом n-й
степени:

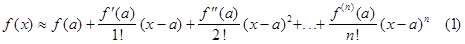
Ряд Тейлора.
Обратимся к формуле (1). Разность между функцией f(x) и её многочленом в правой части
называют отклонением, которое выражается остаточным членом rn(x).Если в формуле
рассматривать всё больше и больше членов, то может оказаться, что отклонение
стремится к нулю, но не для всякой функции и не для любого значения х. Однако
существует широкий класс функций, для которых остаточный член действительно
стремится к нулю при 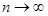 , по крайней мере для значений, заполняющих некоторый
промежуток, содержащий т.а. Именно для таких функций формула Тейлора позволяет
вычислить f(x) с любой
степенью точности. Если
, по крайней мере для значений, заполняющих некоторый
промежуток, содержащий т.а. Именно для таких функций формула Тейлора позволяет
вычислить f(x) с любой
степенью точности. Если 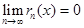 , то из формулы Тейлора следует:
, то из формулы Тейлора следует: 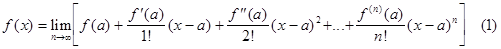
Число слагаемых является неограниченным. Выражение в правой части
формулы называют рядом Тейлора, а функцию f(x)- суммой этого ряда.
Ряд Тейлора можно записать в таком виде:
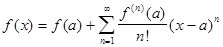 , при а=0
, при а=0 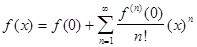 Выражение в правой
части этой формулы называют рядом Маклорена. Получаем:
Выражение в правой
части этой формулы называют рядом Маклорена. Получаем:
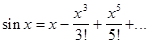
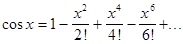
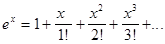
Условие сходимости:
Для разложения f(x)
в степенной ряд (т.е. в ряд Тейлора), необходимо и достаточно, чтобы предел
остаточного члена формулы Тейлора был равен нулю: 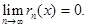
Степенной ряд сходится при любых х или говорят, что его областью
сходимости является промежуток 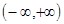 . Из этих формул видно, что sin(-x)=-sinx, т.е. f(x)=sinx- нечётная функция.
. Из этих формул видно, что sin(-x)=-sinx, т.е. f(x)=sinx- нечётная функция.
cos(-x)=cosx,
f(x)=cosx- чётная функция.
Примеры разложения функций в степенные
ряды.
Степенной ряд 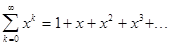 можно рассматривать
как геометрический с первым членом а=1 и знаменателем q=x. Если
можно рассматривать
как геометрический с первым членом а=1 и знаменателем q=x. Если 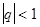 , т.е.
, т.е. 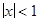 , то данный ряд сходится.
, то данный ряд сходится. 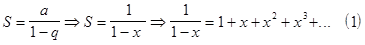 .
.
Мы получили разложение функции 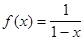 в степенной ряд. Этот
ряд сходится при
в степенной ряд. Этот
ряд сходится при 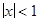 .
.
Аналогичными рассуждениями можно установить, что 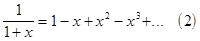 сходится при
сходится при 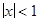 . Степенной ряд можно почленно дифференцировать и
интегрировать, т.е. обращаться с ним как с многочленом.
. Степенной ряд можно почленно дифференцировать и
интегрировать, т.е. обращаться с ним как с многочленом.
В формуле (1) заменим x на t и
проинтегрируем получившийся ряд на промежутке [0,x]; 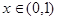
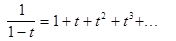 ,
, 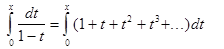
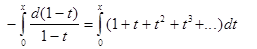
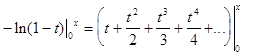
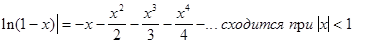
Так же заменим x на
t в формуле (2).
Получим: 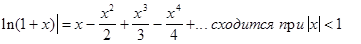
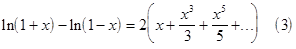
Разложение (3) в степенной ряд сходится при 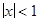 . Оно может быть использовано для вычисления логарифмов
натуральных чисел. Положим в формуле (3)
. Оно может быть использовано для вычисления логарифмов
натуральных чисел. Положим в формуле (3) 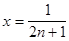 , где n- натуральное
число, 0<x<1, при
любом n ряд в правой
части этой формулы будет сходится.
, где n- натуральное
число, 0<x<1, при
любом n ряд в правой
части этой формулы будет сходится. 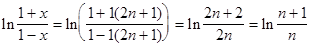
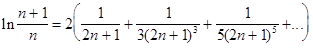
Пользуясь этой формулой, можно последовательно вычислить 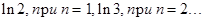
Обратимся снова к формуле (2). Полагая 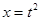 , записываем полученный ряд и интегрируем его по отрезку [0,x], 0<x<1.
, записываем полученный ряд и интегрируем его по отрезку [0,x], 0<x<1. 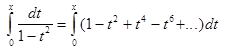
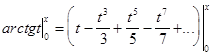

Пусть х=1 в этой формуле 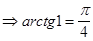
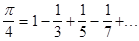 Можно
приближённо вычислить
Можно
приближённо вычислить 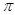 .
.
Биномиальный ряд
Разложим в ряд Маклорена функцию
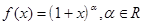
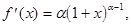
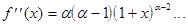
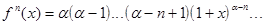 ;
;
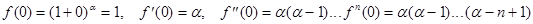 В соответствии с формулой Маклорена:
В соответствии с формулой Маклорена:
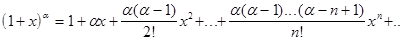
Ряд в правой части называют биномиальным. Можно доказать, что
биномиальный ряд сходится при 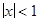 , т.е. областью его сходимости служит интервал (-1,1).
Отметим, что ряд (2) является частным случаем этого ряда при
, т.е. областью его сходимости служит интервал (-1,1).
Отметим, что ряд (2) является частным случаем этого ряда при  .
.
В случае 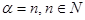 формула принимает вид:
формула принимает вид:
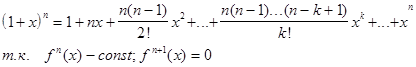
все члены, начиная с n+1-го обращаются в 0. В правой части формулы разложения 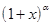 их остаётся конечное
число, ряд обрывается. Эта формула при а=1 является частным случаем бинома
Ньютона.
их остаётся конечное
число, ряд обрывается. Эта формула при а=1 является частным случаем бинома
Ньютона.
Применение рядов в приближённых
вычислениях.
Знакочередующимся рядом называется ряд, у которого любые 2
члена с номерами k и k+1 (k=1,2,3..) имеют противоположные знаки.
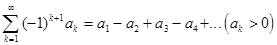
Признак Лейбница сходимости знакочередующегося ряда выражается
следующей теоремой:
Теорема1 Знакочередующийся ряд 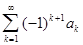 сходится, если модуль
его членов убывают с возрастанием номера k и общий член стремится к 0, т.е., если выполняются 2 условия:
сходится, если модуль
его членов убывают с возрастанием номера k и общий член стремится к 0, т.е., если выполняются 2 условия:
ak+1<ak,
k- нат. число;
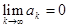
Теорема2 Сумма остатка знакочередующегося ряда,
удовлетворяющего условиям признака Лейбница, имеет знак первого оставшегося
члена и по модулю не превосходит его модуля.
С помощью рядов можем вычислять приближённо значения логарифмов,
корней различной степени, определённых интегралов, тригонометрических функций.
Пусть неизвестное число А каким-то образом представлено сходящимся
рядом:
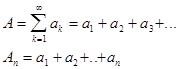 ,где а1...аn- некоторые
числа.
,где а1...аn- некоторые
числа.
Погрешность при замене А на Аn выражается суммой остатка аn=an+1+an+2+... Т.к.
ряд сходится, то 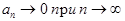 и поэтому при
достаточно большом n погрешность
станет сколь угодно малой. Другими словами, искомое А посредством частичной
суммы Аn указанного ряда можно
выразить с любой заданной точностью.
и поэтому при
достаточно большом n погрешность
станет сколь угодно малой. Другими словами, искомое А посредством частичной
суммы Аn указанного ряда можно
выразить с любой заданной точностью.
Если ряд знакочередующийся, удовлетворяет условиям признака
Лейбница, то сумма остатка имеет знак своего первого члена и по модулю не
превышает его.
В случае ряда с положительными членами 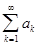 необходимо найти новый
ряд
необходимо найти новый
ряд 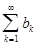 с большими членами
с большими членами 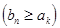 , который бы легко суммировался, и в качестве оценки для
суммы остатка
, который бы легко суммировался, и в качестве оценки для
суммы остатка 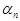 взять сумму
взять сумму 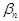 остатка этого ряда.
остатка этого ряда.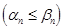
3.3. Ряды Фурье.
Мы показали приближение некоторых функций алгебраическими
многочленами, теперь покажем, как приближаются функции тригонометрическими
многочленами. Инструментом для этого будут ряды Фурье.
Тригонометрическим рядом называют функциональный ряд вида: 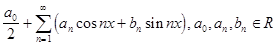 называют
коэффициентами ряда.
называют
коэффициентами ряда.
Пусть данный тригонометрический ряд сходится и его сумма равна f(x). Тогда 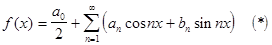 .
.
Тригонометрической системой функций называют бесконечное множество
функций 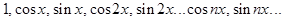 Эта система обладает свойствами:
Эта система обладает свойствами:
1.Определённый интеграл по отрезку 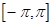 от квадрата любой
функции отличен от 0, причём
от квадрата любой
функции отличен от 0, причём
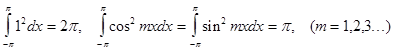
2. Определённый интеграл по отрезку 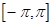 от произведения любых
двух различных функций равен нулю, т.е.
от произведения любых
двух различных функций равен нулю, т.е.
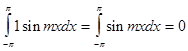 ,
, 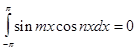 ,
,
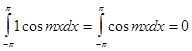 ,
, 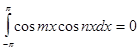 ,
,
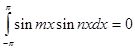
Замечание 1: Система функций 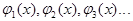 называется
ортогональной на отрезке [a,b],
если
называется
ортогональной на отрезке [a,b],
если
1.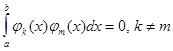
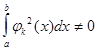
Видим, что тригонометрическая система функций является
ортогональной на отрезке 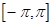 .
.
Будем считать, что выполнено условие, при котором этот
тригонометрический ряд можно интегрировать почленно, тогда его коэффициенты
определяются формулами:
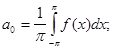
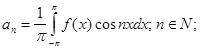
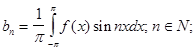
Тригонометрический ряд, определяемый такими коэффициентами,
называется рядом Фурье, а числа an,
bn- коэффициентами Фурье функции f(x).
Замечание 2: Формулы a0 и an
можно объединить в одну: 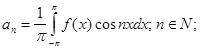
При этом появляется удобство обозначения начального члена
тригонометрического ряда через a0/2,
а не через a0.
 Замечание 3: Два аналитических выражения могут
совпадать в некотором промежутке, но не совпадать при этом на всей числовой
прямой.
Замечание 3: Два аналитических выражения могут
совпадать в некотором промежутке, но не совпадать при этом на всей числовой
прямой.
Пример:





 Y
Y






-2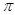 f(x)=x,
f(x)=x, 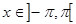
-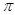 0
0 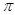 2
2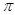 Х
Х
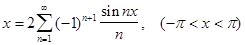 ; S(x)- сумма ряда,
; S(x)- сумма ряда,
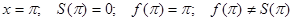
Замечание 4: Тригонометрическим рядом на всей числовой прямой можно
представить только периодическую функцию.
Пример: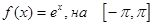
f(x)- ограничена,
непрерывна, монотонна
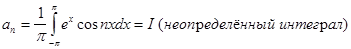
а). 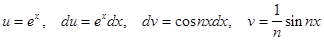
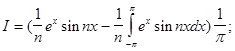
б). 
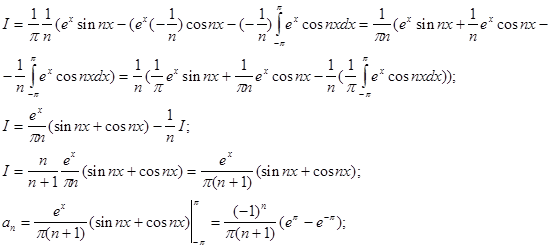 3.
3. 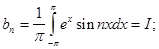

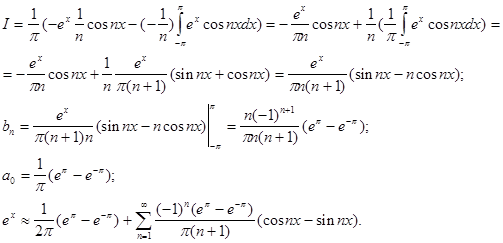
Приближение функций тригонометрическими
многочленами.
Тригонометрическими многочленами n-го порядка называют функцию вида: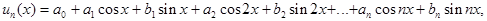 или короче:
или короче: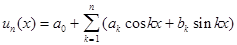 .
.
Рассмотрим сумму первых n членов ряда Фурье: 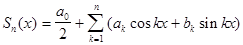 .
.
Эта сумма является тригонометрическим многочленом n-го порядка, начальный член которого
представлен в виде a0/2.
В качестве приближения функции f(x)
с периодом 2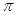 тригонометрическим
многочленом берут указанную сумму Sn(x), т.е.
тригонометрическим
многочленом берут указанную сумму Sn(x), т.е. 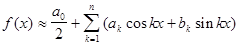 .
.
Естественно, при этом возникает вопрос об ошибке приближения. Если
функция с периодом 2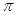 имеет при всех х
производную f®(x) порядка
r, удовлетворяющая
неравенству
имеет при всех х
производную f®(x) порядка
r, удовлетворяющая
неравенству 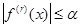 , то можно доказать, что ошибка приближения выражается
следующим неравенством:
, то можно доказать, что ошибка приближения выражается
следующим неравенством: 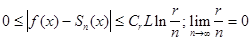 , где Cr-
постоянная, зависящая только от r. Отсюда видно, что ошибка стремится к нулю при n стремящемуся к
бесконечности. Причём тем быстрее, чем больше производных имеет функция.
, где Cr-
постоянная, зависящая только от r. Отсюда видно, что ошибка стремится к нулю при n стремящемуся к
бесконечности. Причём тем быстрее, чем больше производных имеет функция.
Для аналитических функций оценка будет ещё лучше. Аналитической в
области определения называют функцию, которая разлагается в сходящейся к ней
степенной ряд в области определения. Для функция, аналитических на всей
действительной оси, оценка приближения выражается неравенством: 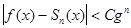 .С и g- положительные
постоянные, связанные с f(x),
q<1.
.С и g- положительные
постоянные, связанные с f(x),
q<1.
И обратно, если для функции f(x) выполняется это неравенство, то она является аналитической.
Можно утверждать: если функция разлагается в сходящийся к ней ряд Фурье, то
отсюда ещё не следует, что она аналитическая. Однако f(x) будет аналитической, если уклонение
от суммы первых n членов
её ряда Фурье имеет оценку, т.е. убывает быстрее члена убывающей геометрической
прогрессии.
Чтобы обеспечить приближение произвольных непрерывных периодических
функций тригонометрическими многочленами, пользуются так называемыми методами
суммирования рядов Фурье. В качестве тригонометрических многочленов,
приближающих функцию, вместо сумм Фурье рассматривают некоторые их
видоизменения. Один из таких методов состоит в следующем: для непрерывной
периодической функции находят её ряд Фурье, который может быть и не сходящимся,
а затем составляется среднее арифметическое первых частичных сумм этого ряда: 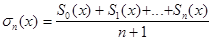 , где
, где 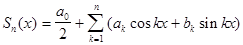 .
.
Среднее арифметическое 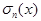 называют суммой Фейера
n-го порядка,
соответствующей данной функции f(x).
Название этих сумм дано в честь венгерского математика Липота Фейера
(1880-1959), который первым предложил указанный метод. Он доказал, что
называют суммой Фейера
n-го порядка,
соответствующей данной функции f(x).
Название этих сумм дано в честь венгерского математика Липота Фейера
(1880-1959), который первым предложил указанный метод. Он доказал, что 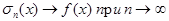 , если f(x)-
непрерывная функция.
, если f(x)-
непрерывная функция.
Заключение.
Теорией приближения функций многочленами занимались такие
математики, как Эйлер, Лаплас, Фурье, Понселе, и, наконец, Чебышев.
У Чебышева, который приступил к задаче о наилучшем устройстве
параллелограмма Уатта, возникли математические вопросы, о которых в то время
знали очень мало. Для решения он разработал метод, названный французским
математиком Жозефом Бертраном
(1822-1900) чудом анализа. Этот метод сохранил своё значение и после
того, как паровые машины, а вместе с ними и параллелограмм Уатта, отошли на
задний план. Созданная Чебышевым теория приближения функций интенсивно
развивалась и развивается сейчас в трудах российских и иностранных учёных. В
терминах этой теории отражена одна из фундаментальных идей математики-
приближение (замена) сложных объектов более простыми и удобными. Эта идея является
основной в вопросах взаимосвязей математики и практики, что стимулировало
развитие теории приближения функций в прошлом и, надо полагать, обеспечит к ней
интерес в будущем.
Вообще теория аппроксимации непрерывных функций многочленами играет
очень большую роль в математики, так же в решении технических проблем. Этот
вопрос ещё до конца не исчерпан и новые открытия ждут своего часа.