4. Деньги стоят j₂ = 5%. Найти датированную сумму по окончании трех лет для платежей: 5 тыс. руб. через пять лет и 8 тыс. руб. через 8 лет.

Решение:

Сначала определим первоначальную сумму для срока 5 лет:

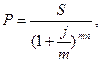
Где: m – количество начислений процентов в году,

n – количество лет,

S – наращенная сумма,

P – первоначальная сумма,

j – процентная ставка.

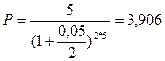 тыс. руб.

Теперь найдем датированную сумму по окончании трех лет для платежа 5 тыс. руб. через пять лет:

тыс. руб.

Далее определим первоначальную сумму для срока 8 лет:

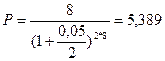 тыс. руб.

Теперь найдем датированную сумму по окончании трех лет для платежа 8 тыс. руб. через восемь лет:

тыс. руб.

5. Найти эффективную ставку, при которой 10 тыс. руб. теперь эквивалентны 20 тыс. руб. через 14 лет.

Решение:

Для определения эффективной ставки воспользуемся следующей формулой:

или 5,07%.

6. При данной процентной ставке j₂ 10 млн. руб. прирастают до 25 млн. руб. через двадцать лет. Какой является сумма в конце 10 лет?

Решение:

Сначала определим процентную ставку по данной операции:

 или 4,62%

Теперь определим сумму в конце 10 лет:

млн. руб.

7. В рассматриваемый год ожидаемая инфляция составляет 20%. Какую номинальную годовую процентную ставку следует установить по вкладам в банке, чтобы реальная годовая ставка равнялась 3%?

Решение:

Вывод формулы для процентной ставки:

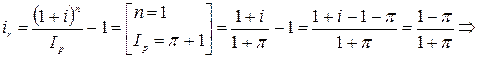
8. Судостроительная фирма желает вносить в банк ежеквартально равные суммы. Банк выплачивает сложные проценты по ставке j₆ = 8%. Какую сумму должна вносить ежеквартально фирма, чтобы за 15 лет накопить 3 млн. руб.?

Решение:

млн. руб.

9. Предприятие создает фонд для постройки нового здания, вкладывая в него каждые 4 года 15 млн. руб. Деньги кладутся в банк, выплачивающий 5% годовых (сложных). Какая сумма будет в фонде через 16 лет?

Решение:

Для решения воспользуемся следующей формулой ренты:

млн. руб.

10. Покупатель приобретает дом, который стоит 50000 руб. Он уплатил сразу 20000 руб., а на остальную сумму получил кредит на 1 год 6 месяцев под 4% годовых (простых), который должен погасить ежемесячными равными уплатами. Чему равна каждая уплата?

Решение:

Сумма кредита составляет: 50000 – 20000 = 30000 руб.

Сумма долга с процентами составит:

S = P*(1 + n*i),

Где: S – наращенная сумма по сертификату,

P – первоначальная сумма,

n – количество лет,

i – процентная ставка.

S = 30000*(1 + 1,5*0,04) = 31800 руб.

Ежемесячная сумма составит: 31800 / 18 = 1766,67 руб.