1. Процентный депозитный сертификат сроком 120 дней в 200 тыс. д. ед. с начислением простых процентов по ставке 25%, учтен в банке за 90 дней по учетной ставке 25%.

Определить: сумму к погашению, дисконт, полученный банком.

Решение:

Для определения суммы к погашению воспользуемся формулой простых процентов:

S = P*(1 + t/k*i),

Где: S – наращенная сумма по сертификату,

P – первоначальная сумма,

t – количество дней, в течении которых начисляется процент,

k – количество дней в году

i – процентная ставка.

Подставляя имеющиеся данные в формулу, мы получим:

S = 200*(1 + 120/360*0,25) = 216,67 тыс. д.ед. – сумма, которую должен был получить вкладчик по сертификату к концу его срока.

Теперь определим дисконт, полученный банком:

Сумма дисконта = S – S(1 – t/k*d)

Где: d – учетная ставка.

Сумма дисконта = 216,67 - 216,67(1 – 90/360*0,25) = 13,55 тыс. д.ед.

2. Вкладчик стремится увеличить сумму вклада в 8 раз за три года. Какая ставка процента устроила бы его?

Решение:

Определим ставку процентов данной операции по следующей формуле:

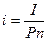
где: I – сумма процентов,

n – количество лет.

I = 8 – 1 = 7

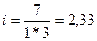 или 233,33% годовых

3. Определите значение учетной ставки, эквивалентной ставке простых процентов, равной 120% годовых.

Решение:

Для определения ставки выведем формулу учетной ставки эквивалентной ставке простого процента.

FV=PV*(1+rn); à FV/PV=1+rn, где FV-будущая стоимость PV-настоящая стоимость, r – процентная ставка, n-период времени.

PV=FV(1-dt);  à FV/PV=1/(1-dt); dt- учетная ставка.

1+rn=1/(1-dt)à 1-dt=1/(1+rn)àdt=rn/(1+rn);

dt=1,2/(1+1,2)=54,5%

4. Какая сумма денег по окончании четырех лет эквивалентна 25 тыс. руб. по окончании 9 лет, если деньги стоят j₄ = 4,5%?

Решение:

Будем использовать формулу:

FV = PV *(1 + j/m)^n*m

Где FV – наращенная сумма через определенный период времени,

PV – текущая стоимость,

j – процентная ставка,

m – количество начислений в год,

n – срок операции.

25*(1+0,0045/4)^9*4=26,033

Х=26,033/(1+0,0045/4)^4*4=25,567

5. Контракт предполагает платежи по 1 тыс. руб. в конце каждого квартала в течении следующего года и дополнительный заключительный платеж 5 тыс. руб. по его окончании. Какова стоимость этого контракта наличными, если деньги стоят j₄ = 5%?

Решение:

Т.к. платежи поступают в конце квартала, то происходит наращивание аннуитета постнумеранда.

FV = PV₁ (1+J(n-1)) + PV₂ (1+J(n-2)) +… +PV_n

FV = 1*(1+0.05/4*3)+ 1*(1+0.05/4*2)+ 1*(1+0.05/4*1)+5 = 8.075 тыс. руб.

6. Найти годовую эффективную норму сложного процента, соответствующую 1,5%, конвертируемым ежемесячно.

Решение:

Эффективная ставка годового начисления процентов, исходя из 1,5% годовых, составит:

i = (1 + j / m)^m - 1 = (1 + 0,015 / 4) - 1 =0,00375.

Эффективная ставка ежемесячного начисления процентов будет равна:

i = (1 + j / m)^m - 1 = (1 + 0,015 / 12)¹² - 1 = 0,015.

Таким образом, годовая ставка, эквивалентная номинальной ставке процентов в размере 1,5% годовых при ежемесячном начислении процентов, составит 1,5% против 0,375% с ежегодным начислением процентов. Чем больше периодов начисления, тем быстрее идет процесс наращения.

7. Базовая годовая сумма оплаты обучения в вузе равна 2000 руб. и повышается с учетом инфляции 15%. Срок обучения 5 лет. Вуз предлагает выплатить сразу 10 тыс. руб., оплатив весь срок обучения. Выгодно ли это предложение для обучаемого? Банковский процент на вклад составляет 13%, сумма вклада 14 тыс. руб.

Решение:

Определим наращенную сумму через пять лет, с учетом инфляции, для этого воспользуемся формулой сложных процентов, учитывающих уровень инфляции:

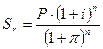
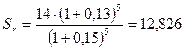 тыс. руб.

Теперь определим сумму затрат на обучение за пять лет при уровне инфляции 15%:

За первый год – 2000 руб.

За второй год – 2000(1 + 0,15)¹ = 2300 руб.

За третий год – 2000(1 + 0,15)² = 2645 руб.

За четвертый год – 2000(1 + 0,15)³ = 3041 руб.

За пятый год – 2000(1 + 0,15)⁴ = 3498 руб.

Теперь рассчитаем общую сумму платежей: 2000 + 2300 + 2645 + 3041 + 3498 = 13484 руб.

Данное предложение для обучаемого будет выгодным.

8. Семья хочет через 6 лет купить дачу за 12000 тыс. д.ед. Какую сумму (одинаковую) ей нужно каждый год из этих 6 лет добавлять на свой счет в банке, чтобы накопить эти деньги, если годовая ставка процента в банке 8%?

Решение:

n=6

S=12000

J=0,08

p=m=1

R=?

12000=R*((1+0,08)⁶-1)/0,08)

R=12000/7,335=1635,99

9. Замените годовую десятилетнюю ренту с годовым платежом 1000 д.ед. на ренту с полугодовыми платежами по 600 д.ед. Годовая ставка процента 8%.

Решение:

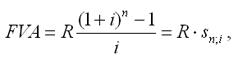
где FVA – наращенная сумма ренты;

R – размер члена ренты, т.е. размер очередного платежа;

i – годовая процентная ставка, по которой на платежи начисляются сложные проценты;

n – срок ренты в годах,

s _n;i – коэффициент наращения ренты.

FVA =(1000*(1+0,08)¹⁰-1)/0,08=14486,56

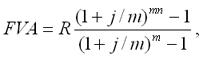
600*((1+0,04)^20--1)/(1+0,04)¹⁰-1)=616,629

Такая замена ренты требует значительно увеличить срок ренты..

10. Проверьте план погашения основного долга равными годовыми уплатами, рассчитанный с помощью компьютера.

Процентная годовая ставка 8%       Величина займа 600 д.ед.
Уплаты	168,0	158,4	148,8	139,2	129,6
Годы	1	2	3	4	5

Решение:

Величина погашения долга определяется следующим образом:

d_t = D : n = const,

где d_t – величина погашения основной суммы долга;

D – первоначальная сумма долга;

n – срок долга в годах;

t – номер года, t = 1, 2, …, n.

Проценты начисляются на уменьшаемую сумму основного долга:

I_t = D_t • q ,

где D_t – остаток долга на начало очередного года;

q – ставка процентов, начисляемых на сумму долга.

Тогда размер срочной уплаты можно представить как сумму процентов и сумму погашения долга:

Y_t = I_t + d_t ,

где Y_t – срочная уплата на конец текущего года.

d=600/5=120

I₁=600*0,08=49,8

Y₁=169,8

I₂=480*0,08=38,4

Y₂=158,4

I₃=360*0.08=28.8

Y₃=148.8

I₄=240*0.08=19.2

Y₄=139.2

I₅=120*0.08=9.6

Y₅=129.6

Таким образом, за исключением первого года суммы рассчитаны верно.