Глава II. Из
опыта организации интеллектуального развития школьников.
2.1. Методики исследования
интеллектуальных умений школьников и анализ опытной работы.
Экспериментальная программа была проверена в 9 «б» классе.
В классе 28
учащихся, из них 15 мальчиков и 13 девочек. Физически и умственно все дети
здоровы. С ослабленным здоровьем – Денис Ф.
Преобладающее
большинство детей в классе – холерики. Отсюда их подвижность, энергия,
шумливость, темперамент.
По
способностям класс средний, заниматься на «4» и «5» могут большинство ребят.
Слабы в учебе Паша А., Саша С., Дима Л., хорошие способности у Андрея Б.,
Сережи Б., Юли К., Оксаны К., Георгия К.
Совсем нет
желания и интереса к учебе у Димы Л.
Саша С. и Дима
Л. имеют слабые способности, не сосредоточены, рассеяны на уроке, не успевают
за классом. Требуют особого, постоянного контроля со стороны учителя и
родителей.
Желание
учиться у большинства детей есть, и это радует.
Особую тревогу
вызывают Саша С. и Дима Л., так как со стороны родителей нет должного контроля
за этими детьми, за их занятиями, за их учебой. Мальчики недисциплинированны,
постоянно приходят с невыученными уроками.
В целом класс
очень активный, требует на уроках большой нагрузки и постоянной занятости в
свободное время.
Проведенное
исследование включало 3 серии эксперимента:
1)
констатирующая;
2)
обучающая;
3)
контрольная.
Для того,
чтобы успешно организовать исследовательскую работу, нам необходимо было
изучить уровень интеллектуального развития учащихся. В своей дипломной работе
мы уделили больше внимания одному компоненту интеллектуального развития, а
именно мышлению. Мы использовали ряд методик по изучению уровня развития умения
мыслить, которые позволили нам получить первоначальный результат.
С целью
установления индивидуальных особенностей скорости протекания мыслительного
процесса у учащихся была проведена методика 1.
Методика 1. Скорость протекания мыслительного процесса.
Ход
выполнения задания.
Учащимся
предъявляется написанная на плакате или доске таблица слов с пропущенными
буквами. Ученики по команде начинают писать те полные слова, которые они сумели
образовать, вставив пропущенные буквы. Учитель фиксирует время завершения работы
каждым учеником.
Необходимый
материал: секундомер, список слов с пропущенными буквами.
Список
слов:
|
п – ро
|
д – р – во
|
п – л – а
|
|
г – ра
|
з – м – к
|
о – р – г
|
|
п – ле
|
к – м – нь
|
к – р – он
|
|
к – са
|
с – р – й
|
з – р – о
|
|
т – ло
|
п – в – д
|
в – с – ок
|
|
п – ля
|
х – л – д
|
с – г – об
|
|
в – ра
|
п – с – к
|
в – т – а
|
|
с – ла
|
к – з – л
|
п – д – ак
|
|
д – ма
|
з – л – нь
|
п – р – а
|
|
р - ка
|
т – л – га
|
б – л – он
|
|
з – о – ок
|
с – я – о – ть
|
|
|
к – н – а
|
к – с – а – ник
|
|
|
с – е – ло
|
у – и – е – ль
|
|
|
к – ы – а
|
а – е – ь – ин
|
|
|
т – а - а
|
с – а – ц – я
|
|
|
к – у – ка
|
ч – р – и – а
|
|
|
с – а – ка
|
к – п – с – а
|
|
|
т – у – а
|
с – а – о – ть
|
|
|
с – а – а
|
с – е – о – а
|
|
|
п – е – а
|
к – н – о - а
|
|
Обработка
данных.
На основе
составления результатов отдельных испытуемых со среднегрупповым делается вывод
о скорости протекания мыслительных процессов.
Результаты
выполнения методики представлены в таблице 1.
Таблица 1.
|
№
|
Учащиеся
|
Время
|
Скорость
протекания мыслительного процесса
|
|
низкая
|
средняя
|
высокая
|
|
1.
|
Павел А.
|
19м.15с.
|
+
|
|
|
|
2.
|
Андрей Б.
|
14м.30с.
|
|
|
+
|
|
3.
|
Яна Б.
|
17м.10с.
|
|
+
|
|
|
4.
|
Рома Б.
|
17м.20с.
|
|
+
|
|
|
5.
|
Сережа Б.
|
14м.15с.
|
|
|
+
|
|
6.
|
Аня Г.
|
16м.45с.
|
|
+
|
|
|
7.
|
Игорь Г.
|
20м.10с.
|
+
|
|
|
|
8.
|
Костя Е.
|
14м.50с.
|
|
|
+
|
|
9.
|
Аня И.
|
17м.20с.
|
|
+
|
|
|
10.
|
Вова К.
|
17м.15с.
|
|
+
|
|
|
11.
|
Юля К.
|
14м.40с.
|
|
|
+
|
|
12.
|
Оксана К.
|
14м.10с.
|
|
|
+
|
|
13.
|
Ксения К.
|
17м.05с.
|
|
+
|
|
|
14.
|
Георгий К.
|
13м.50с.
|
|
|
+
|
|
15.
|
Надя К.
|
16м.45с.
|
|
+
|
|
|
16.
|
Маша К.
|
16м.40с.
|
|
+
|
|
|
17.
|
Катя Л.
|
17м.05с.
|
|
+
|
|
|
18.
|
Дима Л.
|
20м.15с.
|
+
|
|
|
|
19.
|
Оксана Л.
|
15м.40с.
|
|
+
|
|
|
20.
|
Сережа П.
|
16м.00с.
|
|
+
|
|
|
21.
|
Эля Р.
|
16м.05с.
|
|
+
|
|
|
22.
|
Саша С.
|
19м.55с.
|
+
|
|
|
|
23.
|
Марина С.
|
14м.20с.
|
|
|
+
|
|
24.
|
Сережа С.
|
16м.50с.
|
|
+
|
|
|
25.
|
Миша С.
|
16м.45с.
|
|
+
|
|
|
26.
|
Денис Ф.
|
20м.30с.
|
+
|
|
|
|
27.
|
Женя Ф.
|
15м.15с.
|
|
+
|
|
|
28.
|
Аня Ч.
|
16м.35с.
|
|
+
|
|
|
Среднегрупповое
время
|
16м.41с.
|
|
Как видно из
таблицы, у 25% учащихся высокая скорость протекания мыслительного процесса, у
18% - низкая и у 57% - средняя.
С целью
изучения индивидуальных особенностей уровней развития мыслительных операций:
анализа, синтеза, обобщение была проведена методика 2.
Методика 2. Поиск закономерностей числовых рядов.
Ход выполнения задания.
Учащимся
предъявляется таблица, на которой напечатаны 10 рядов чисел. Рассматривая в
отдельности каждый из данных 10 рядов, испытуемый должен найти правило, по которому
подобранны числа и написать справа от ряда еще 2 числа, которые продолжили бы
этот ряд.
Необходимый
материал: таблица с рядами чисел, секундомер.
|
Таблица с
числами
|
|
Ответы
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
|
1
|
2
|
4
|
8
|
16
|
32
|
64
|
128
|
|
4
|
5
|
8
|
9
|
12
|
13
|
16
|
17
|
|
19
|
16
|
14
|
11
|
9
|
6
|
4
|
1
|
|
29
|
28
|
26
|
23
|
19
|
14
|
8
|
1
|
|
16
|
8
|
4
|
2
|
1
|
1/2
|
1/4
|
1/8
|
|
1
|
4
|
9
|
16
|
25
|
36
|
49
|
64
|
|
21
|
18
|
16
|
15
|
12
|
10
|
9
|
6
|
|
3
|
6
|
8
|
16
|
18
|
36
|
38
|
76
|
Обработка
данных.
На основе
сопоставления результатов отдельных испытуемых со среднегрупповыми делается
вывод об уровне развития мыслительных операций.
Данные по
выполнению задания представлены в таблице 2.
Таблица 2.
|
№
|
Учащиеся
|
Время
|
Уровень развития
мыслительных операций
|
|
низкий
|
средний
|
высокий
|
|
1.
|
Павел А.
|
8м.10с.
|
+
|
|
|
|
2.
|
Андрей Б.
|
4м.50с.
|
|
|
+
|
|
3.
|
Яна Б.
|
6м.05с.
|
|
+
|
|
|
4.
|
Рома Б.
|
4м.25с.
|
|
|
+
|
|
5.
|
Сережа Б.
|
4м.10с.
|
|
|
+
|
|
6.
|
Аня Г.
|
6м.10с.
|
|
+
|
|
|
7.
|
Игорь Г.
|
7м.35с.
|
+
|
|
|
|
8.
|
Костя Е.
|
4м.15с.
|
|
|
+
|
|
9.
|
Аня И.
|
6м.25с.
|
|
+
|
|
|
10.
|
Вова К.
|
6м.10с.
|
|
+
|
|
|
11.
|
Юля К.
|
5м.15с.
|
|
|
+
|
|
12.
|
Оксана К.
|
6м.30с.
|
|
+
|
|
|
13.
|
Ксения К.
|
6м.40с.
|
|
+
|
|
|
14.
|
Георгий К.
|
4м.35с.
|
|
|
+
|
|
15.
|
Надя К.
|
6м.30с.
|
|
+
|
|
|
16.
|
Маша К.
|
6м.35с.
|
|
+
|
|
|
17.
|
Катя Л.
|
6м.50с.
|
|
+
|
|
|
18.
|
Дима Л.
|
7м.45с.
|
+
|
|
|
|
19.
|
Оксана Л.
|
6м.05с.
|
|
+
|
|
|
20.
|
Сережа П.
|
6м.45с.
|
|
+
|
|
|
21.
|
Эля Р.
|
6м.45с.
|
|
+
|
|
|
22.
|
Саша С.
|
7м.20с.
|
+
|
|
|
|
23.
|
Марина С.
|
4м.55с.
|
|
|
+
|
|
24.
|
Сережа С.
|
6м.15с.
|
|
+
|
|
|
25.
|
Миша С.
|
7м.50с.
|
+
|
|
|
|
26.
|
Денис Ф.
|
7м.40с.
|
+
|
|
|
|
27.
|
Женя Ф.
|
8м.05с.
|
+
|
|
|
|
28.
|
Аня Ч.
|
6м.20с.
|
|
+
|
|
|
Среднегрупповое
время
|
6м.28с.
|
|
Из таблицы
видно, что у 25% учащихся высокий уровень развития мыслительных операций, у
25%-низкий и у 50%-средний.
С целью определения способности выделять
существенное (способности к абстрагированию) была проведена методика 3.
Методика 3. Исключение.
Ход
выполнения задания.
Учащимся
предлагается 5 рядов слов. В каждом из рядов даются в скобках, а одно – перед
ними. Ученики должны за специально отведенное время (1,5 мин.) исключить из
скобок (т.е. выделить) 2 слова, наиболее существенны для слова перед скобками.
Необходимый
материал.
Сад (растение, садовник, собака, забор, земля).
Ответ: растение, земля.
Река (берег, рыба, вода, рыболов, тина).
Ответ: берег, вода.
Куб (углы, чертеж, сторона, камень, дерево).
Ответ: углы, сторона.
Чтение (глаза, книга, картина, печать, слово).
Ответ: глаза, печать.
Игра (шахматы, игроки, штрафы, правила, наказание).
Ответ: игроки, правила.
Обработка
данных.
Учащиеся,
которые правильно выполнили задание, очевидно обладают умением выделять
существенное. Те, кто допустил ошибки (или просто не выполнил), не умеют отличить
существенные и несущественные признаки, то есть такая способность у них не развита.
Результаты
выполнения методики представлены в таблице 3.
Таблица 3.
|
№
|
Учащиеся
|
Способность к
абстрагированию
|
|
низкая
|
средняя
|
высокая
|
|
1.
|
Павел А.
|
|
+
|
|
|
2.
|
Андрей Б.
|
|
|
+
|
|
3.
|
Яна Б.
|
|
|
+
|
|
4.
|
Рома Б.
|
|
|
+
|
|
5.
|
Сережа Б.
|
|
|
+
|
|
6.
|
Аня Г.
|
|
+
|
|
|
7.
|
Игорь Г.
|
|
+
|
|
|
8.
|
Костя Е.
|
|
|
+
|
|
9.
|
Аня И.
|
|
+
|
|
|
10.
|
Вова К.
|
|
+
|
|
|
11.
|
Юля К.
|
|
|
+
|
|
12.
|
Оксана К.
|
|
|
+
|
|
13.
|
Ксения К.
|
|
|
+
|
|
14.
|
Георгий К.
|
|
|
+
|
|
15.
|
Надя К.
|
|
+
|
|
|
16.
|
Маша К.
|
|
+
|
|
|
17.
|
Катя Л.
|
|
+
|
|
|
18.
|
Дима Л.
|
|
+
|
|
|
19.
|
Оксана Л.
|
|
|
+
|
|
20.
|
Сережа П.
|
|
+
|
|
|
21.
|
Эля Р.
|
|
+
|
|
|
22.
|
Саша С.
|
|
+
|
|
|
23.
|
Марина С.
|
|
|
+
|
|
24.
|
Сережа С.
|
|
+
|
|
|
25.
|
Миша С.
|
|
+
|
|
|
26.
|
Денис Ф.
|
|
+
|
|
|
27.
|
Женя Ф.
|
|
+
|
|
|
28.
|
Аня Ч.
|
|
+
|
|
Как видно из таблицы, 39% учащихся
класса имеют высокую способность выделять существенное и 61% - среднюю
.
С целью
установления уровня развития у учащихся способности классификации, была
проведена методика 4.
Методика 4. Способность к классификации. Найди лишнее слово.
Ход
выполнения задания.
Учащимся
предъявляется 10 рядов слов по 5 слов в каждом ряду. Их модно классифицировать
различным образом. При правильном «раскладе» остается лишнее слово, которое не
подходит к остальным четырем. Существует один, наиболее верный способ, все
остальные варианты менее очевидны. Имеется качество или характеристика,
которому удовлетворяют 4 слова, но не удовлетворяет одно, которое и должно быть
изъято из ряда. Учащимся предлагается подчеркнуть это слово.
Необходимый
материал: листок с рядами слов:
1.
Птица, самолет, пчела, машина, бабочка.
2.
Смотреть, таращится, глядишь, наблюдаешь, моргать.
3.
Дождь, снег, молния, град, изморозь.
4.
Хлопок, шерсть, нейлон, лен, шелк.
5.
Безжизненный, апатичный, вялый, оцепенелый,
чувствительный.
6.
Бук, ясень, ель, ива, клен.
7.
Превосходный, поэтичный, величавый, грациозный, величественный.
8.
Канатоходец, акробат, клоун, шут, жонглер.
9.
Растирать, нарезать, толочь, измельчать, дробить.
10. Нарцисс,
гладиолус, подснежник, хризантема, тюльпан.
Обработка
данных.
Подчеркивается
число правильно выделенных слов. Доля верно выделенных слов в процентах
показывает уровень развития у ученика способности к классификации.
Результаты
выполнения методики представлены в таблице 4.
Таблица 4.
|
№
|
Учащиеся
|
Показатель, %
|
Уровень развития
способности к классификации
|
|
низкий
|
средний
|
высокий
|
|
1.
|
Павел А.
|
80
|
|
+
|
|
|
2.
|
Андрей Б.
|
90
|
|
|
+
|
|
3.
|
Яна Б.
|
90
|
|
|
+
|
|
4.
|
Рома Б.
|
100
|
|
|
+
|
|
5.
|
Сережа Б.
|
100
|
|
|
+
|
|
6.
|
Аня Г.
|
70
|
|
+
|
|
|
7.
|
Игорь Г.
|
60
|
+
|
|
|
|
8.
|
Костя Е.
|
80
|
|
+
|
|
|
9.
|
Аня И.
|
80
|
|
+
|
|
|
10.
|
Вова К.
|
80
|
|
+
|
|
|
11.
|
Юля К.
|
90
|
|
|
+
|
|
12.
|
Оксана К.
|
90
|
|
|
+
|
|
13.
|
Ксения К.
|
90
|
|
|
+
|
|
14.
|
Георгий К.
|
100
|
|
|
+
|
|
15.
|
Надя К.
|
80
|
|
+
|
|
|
16.
|
Маша К.
|
70
|
|
+
|
|
|
17.
|
Катя Л.
|
60
|
+
|
|
|
|
18.
|
Дима Л.
|
60
|
+
|
|
|
|
19.
|
Оксана Л.
|
100
|
|
|
+
|
|
20.
|
Сережа П.
|
70
|
|
+
|
|
|
21.
|
Эля Р.
|
80
|
|
+
|
|
|
22.
|
Саша С.
|
40
|
+
|
|
|
|
23.
|
Марина С.
|
100
|
|
|
+
|
|
24.
|
Сережа С.
|
80
|
|
+
|
|
|
25.
|
Миша С.
|
90
|
|
|
+
|
|
26.
|
Денис Ф.
|
50
|
+
|
|
|
|
27.
|
Женя Ф.
|
70
|
|
+
|
|
|
28.
|
Аня Ч.
|
80
|
|
+
|
|
Из таблицы
видно, что из всего класса 39% учащихся имеют высокий уровень развития
способности, 19% - низкий и 42% - средний.
С целью
установления уровня развития у учащихся умения сравнивать предметы, понятия,
была проведена методика 5.
Методика 5. Сравнение понятий.
Ход
выполнения задания.
Испытуемому
показываются пары слов и предлагается указать сходства и различия этих явлений
или предметов, обозначаемых приведенными словами.
Необходимый
материал.
Испытуемым
дается два слова явно относящиеся к одной категории. Во вторых, предлагаются
два слова, у которых общее найти трудно и которые гораздо больше отличаются
друг от друга, чем в предыдущем случае. Третья группа задач еще сложнее – это
задачи на сравнение и различение объектов, где различия выражены гораздо
больше, чем сходство.
1.
Корова – лошадь.
2.
Ворона – рыба.
3.
Всадник – лошадь.
Обработка
данных.
Подсчитывается
количество выделенных испытуемым в каждой паре черт сходства и различия.
Высокий уровень развития операции сравнения отличается в том случае, когда
школьник назвал 16-20 черт, средний – 10-15 черт, низкий – менее 10 черт. Важно
учесть, какие черты отметил учащийся в большем количестве – черты сходства или
различия.
Данные по
выполнению задания представлены в таблице 5.
Таблица 5.
|
№
|
Учащиеся
|
Число названных
черт сходства и различия
|
Уровень развития
операции сравнения
|
|
низкий
|
средний
|
высокий
|
|
1.
|
Павел А.
|
7
|
+
|
|
|
|
2.
|
Андрей Б.
|
16
|
|
|
+
|
|
3.
|
Яна Б.
|
13
|
|
+
|
|
|
4.
|
Рома Б.
|
18
|
|
|
+
|
|
5.
|
Сережа Б.
|
11
|
|
+
|
|
|
6.
|
Аня Г.
|
11
|
|
+
|
|
|
7.
|
Игорь Г.
|
8
|
+
|
|
|
|
8.
|
Костя Е.
|
10
|
|
+
|
|
|
9.
|
Аня И.
|
16
|
|
|
+
|
|
10.
|
Вова К.
|
10
|
|
+
|
|
|
11.
|
Юля К.
|
17
|
|
|
+
|
|
12.
|
Оксана К.
|
16
|
|
|
+
|
|
13.
|
Ксения К.
|
11
|
|
+
|
|
|
14.
|
Георгий К.
|
17
|
|
|
+
|
|
15.
|
Надя К.
|
10
|
|
+
|
|
|
16.
|
Маша К.
|
11
|
|
+
|
|
|
17.
|
Катя Л.
|
11
|
|
+
|
|
|
18.
|
Дима Л.
|
6
|
+
|
|
|
|
19.
|
Оксана Л.
|
16
|
|
|
+
|
|
20.
|
Сережа П.
|
12
|
|
+
|
|
|
21.
|
Эля Р.
|
12
|
|
+
|
|
|
22.
|
Саша С.
|
7
|
+
|
|
|
|
23.
|
Марина С.
|
13
|
|
+
|
|
|
24.
|
Сережа С.
|
10
|
|
+
|
|
|
25.
|
Миша С.
|
10
|
|
+
|
|
|
26.
|
Денис Ф.
|
8
|
+
|
|
|
|
27.
|
Женя Ф.
|
11
|
|
+
|
|
|
28.
|
Аня Ч.
|
16
|
|
|
+
|
Как видно из
таблицы, у 29% учащихся высокий уровень развития умения сравнивать предметы,
понятия, у 18% - низкий и у 53% - средний.
С целью
определения у учащихся уровня развития способности оперировать в мышлении
пространственными образами, была проведена методика 6.
Методика 6. Пространственная сообразительность.
Ход
выполнения задания.
Учащимся
предлагается решить задачи на сообразительность, не требующие каких-либо
громоздких вычислений, рассуждений. Задачи могли быть 3х типов.
I.
«Движение». Особенность этих задач состоит в том, что
они требуют от школьника учения совершать такие мыслительные преобразования,
операции, которые видоизменяют лишь местоположение имеющихся у него в
представлении образцов, перемещают их, но не затрагивают их структурных,
композиционных, особенностей.
II.
«Реконструкция».
При решении задач этого типа меняется не только
местоположение имеющегося в представлении образа, но и его структура, строение.
III.
«композиция».
Решение этих задач требует умения от школьника изменять
образ и по местоположению, и по структуре одновременно и неоднократно совершать
не одномоментные отдельные операции, а их композиции.
Ученику
предлагается решить задачи всех трех типов, начиная с третьего.
Необходимый
материал.
I.
1) Укажите несколько букв (слов), запись которых имеет
ось симметрии.
2) Сейчас 2ч. 45м. Сколько будет времени,
когда минутная стрелка повернется на 210 градусов?
II.
1) Разрезать прямоугольник со сторонами 4 и 9 ед. на
две равные части таким образом, что бы, сложив их надлежащим образом, получить
квадрат.
2) В квадрате через верхнюю левую вершину
провели диагональ. Нижний прямоугольник оставили на месте, а верхний повернули
вокруг этой вершины против часовой стрелки на 270 градусов. Какая фигура
образовалась в результате?
III. Квадратный
лист сложили вдвое по диагонали, затем еще раз вдвое так, что получился
равнобедренный треугольник. Какая образуется фигура, если каждую вершину
последнего треугольника отрезать по линии одинаковой длины, параллельной противоположным
сторонам, и развернуть лист?
Обработка
данных.
Решение задач
определенного типа (первого, второго, третьего) соответствует определенному
уровню пространственного мышления. Третий уровень самый высокий. Поэтому, если
ученик решил задачу на третий тип ориентирования, то более простые задачи первого
и второго типа ему уже можно не предлагать. Если он задачу третьего уровня не
смог решить, то ему предлагают задачу второго уровня. Если и ее он не сможет
решить, то дают задачу первого уровня.
Результаты выполнения методики представлены
в таблице 6.
|
№
|
Учащиеся
|
Уровень развития
пространственного мышления
|
|
низкий
|
средний
|
высокий
|
|
1.
|
Павел А.
|
+
|
|
|
|
2.
|
Андрей Б.
|
|
|
+
|
|
3.
|
Яна Б.
|
|
+
|
|
|
4.
|
Рома Б.
|
|
+
|
|
|
5.
|
Сережа Б.
|
|
|
+
|
|
6.
|
Аня Г.
|
|
+
|
|
|
7.
|
Игорь Г.
|
+
|
|
|
|
8.
|
Костя Е.
|
|
+
|
|
|
9.
|
Аня И.
|
|
+
|
|
|
10.
|
Вова К.
|
|
+
|
|
|
11.
|
Юля К.
|
|
|
+
|
|
12.
|
Оксана К.
|
|
+
|
|
|
13.
|
Ксения К.
|
|
+
|
|
|
14.
|
Георгий К.
|
|
|
+
|
|
15.
|
Надя К.
|
|
+
|
|
|
16.
|
Маша К.
|
|
+
|
|
|
17.
|
Катя Л.
|
+
|
|
|
|
18.
|
Дима Л.
|
+
|
|
|
|
19.
|
Оксана Л.
|
|
+
|
|
|
20.
|
Сережа П.
|
+
|
|
|
|
21.
|
Эля Р.
|
|
+
|
|
|
22.
|
Саша С.
|
+
|
|
|
|
23.
|
Марина С.
|
|
+
|
|
|
24.
|
Сережа С.
|
|
+
|
|
|
25.
|
Миша С.
|
+
|
|
|
|
26.
|
Денис Ф.
|
+
|
|
|
|
27.
|
Женя Ф.
|
+
|
|
|
|
28.
|
Аня Ч.
|
+
|
|
|
Из таблицы
видно, что 25% учащихся имеют высокий уровень развития способности оперировать
в мышлении пространственными образами, 36% - низкий и 39% - средний.
С целью
установления наличия интуитивных способностей была проведена методика 7.
Методика 7. Сила интуиции.
Ход
выполнения задания и необходимый материал.
Учащимся
предлагается из двух вариантов ответа на вопросы выбрать тот, который ближе
всего.
1.
Если у меня нет готового ответа, я:
а) спокоен;
б) не спокоен.
2.
В ситуации неопределенности я:
а) дезориентирован (пасую):
б) спокоен, собран.
3.
В ситуациях соревнования я глубоко увлечен:
а) почти всегда;
б) редко.
4.
Если моя интуиция противоречит фактам, обычно я:
а) верю чувствам;
б) следую логике.
5.
Решая сложную проблему, я:
а) сосредоточен на поиске ее
решения;
б) жду, когда придет решение.
6.
Если я не согласен с мнением других людей, я:
а) заявляю об этом открыто;
б) держу свое мнение при себе.
7.
В целом я:
а) предпочитаю (действовать
наверняка) старые уже испытанные способы и пути;
б) люблю рисковать.
8.
Решая проблему, я меняю стратегию:
а) редко;
б) часто.
9.
Я предпочитаю, чтобы мне говорили:
а) как я должен делать;
б) что должно быть сделано.
10. Если
ситуация осложняется, я:
а) оживляюсь;
б) волнуюсь.
11. Сталкиваясь
с проблемой, обычно я:
а) сначала намечаю план и
направление работы;
б) сразу погружаюсь в работу.
12. В
большинстве случаев:
а) всякие изменения нервируют
меня;
б) я рад неожиданным
изменениям.
13. Я
читаю:
а) о разных существах, в том
числе и вымышленных;
б) фактический материал,
относящийся к работе (занятиям).
14. Если
мое мнение отличается от мнения специалиста, я обычно:
а) полагаюсь на себя;
б) считаюсь с авторитетом.
15. Когда
по работе я сталкиваюсь одновременно с несколькими заданиями, я:
а делаю их параллельно;
б) делаю их последовательно.
16. В
учебе (при усвоении нового) я:
а) сначала усваиваю правила и
инструкции;
б) приступаю к самому
материалу, а правила учу уже по ходу дела.
17. В
работе я предпочитаю:
а) следовать установленным
правилам и предписаниям;
б) создаю и следую
собственному порядку.
18. В
школе мне лучше даются:
а) ответы на открытые вопросы
(типы сочинений, размышление и т.п.);
б) ответы на закрытые вопросы
(краткие: да, нет, столько и т.п.).
19. В
основном я:
а) идеалист;
б) реалист.
20. Когда
я ошибаюсь, я:
а) проверяю себя еще раз;
б) забываю об этом и продолжаю
дальше.
21. В
разных ситуациях:
а) я обычно могу объяснить,
откуда я знаю что-либо;
б) обычно не могу этого
объяснить.
22. При
описании и объяснении я больше опираюсь:
а) на аналогичные эпизоды;
б) на факты и примеры.
23. Меня
обычно можно убедить:
а) обращаясь к смыслу;
б) обращаясь к эмоциям.
24. Если
я не прав, я:
а) охотно признаю это;
б) защищаюсь.
25. Скорее
всего, я:
а) фантазер;
б) практик.
26. Решая
сложную проблему, я:
а) прошу совета;
б) стараюсь справится сам.
27. Непредсказуемые
люди:
а) раздражают меня;
б) они мне интересны.
28. Получая
задание на следующую неделю, я обычно говорю:
а) «Давайте договоримся о
точном времени»;
б) «Сообщите мне за один
день».
29. Если
мои планы нарушаются, я:
а) расстраиваюсь;
б) спокойно принимаю новый
план.
30. К
своим догадкам я отношусь:
а) с энтузиазмом;
б) с недоверием.
31. Большинство
моих друзей и коллег:
а) верят в интуицию;
б) относятся к ней
скептически.
32. Меня
считают:
а) человеком «идеи»;
б) человеком «детали».
Обработка
данных.
Подчитывается
общее число баллов. Если общая оценка 24 балла и больше, то испытуемый обладает
тенденцией интуитивного подхода к принятию решения и проблемам. В основном этот
человек полагается на свою интуицию и, возможно, она его не обманывает.
Оценка 16-23.
Испытуемый склонен менять (варьировать) свой стиль, но преобладает интуиция, а
не анализ и синтез. Интуиция чаще инстинктивна, чем ошибочна.
Оценка 8-15. У
испытуемого смешанный стиль, но ближе к анализу и синтезу, рациональному.
Интуиция может его подводить.
Оценка меньше
8. У испытуемого преобладает системно-рациональный подход к проблемам. Он не
доверят своей интуиции, так как она в прошлом его подводила.
Данные по
выполнению задания представлены в таблице 7.
Таблица 7.
|
№
|
Учащиеся
|
Общий балл
|
Интуи-тивный
подход
|
Смешанный стиль
|
Смешанно-рациональный
подход
|
|
Преобладает интуиция
|
Ближе к рациональ-ному
|
|
1.
|
Павел А.
|
13
|
|
|
+
|
|
|
2.
|
Андрей Б.
|
10
|
|
|
+
|
|
|
3.
|
Яна Б.
|
23
|
|
+
|
|
|
|
4.
|
Рома Б.
|
14
|
|
|
+
|
|
|
5.
|
Сережа Б.
|
13
|
|
|
+
|
|
|
6.
|
Аня Г.
|
10
|
|
|
+
|
|
|
7.
|
Игорь Г.
|
23
|
|
+
|
|
|
|
8.
|
Костя Е.
|
22
|
|
+
|
|
|
|
9.
|
Аня И.
|
22
|
|
+
|
|
|
|
10.
|
Вова К.
|
13
|
|
|
+
|
|
|
11.
|
Юля К.
|
16
|
|
+
|
|
|
|
12.
|
Оксана К.
|
21
|
|
+
|
|
|
|
13.
|
Ксения К.
|
9
|
|
|
+
|
|
|
14.
|
Георгий К.
|
17
|
|
+
|
|
|
|
15.
|
Надя К.
|
13
|
|
|
+
|
|
|
16.
|
Маша К.
|
13
|
|
|
+
|
|
|
17.
|
Катя Л.
|
13
|
|
|
+
|
|
|
18.
|
Дима Л.
|
11
|
|
|
+
|
|
|
19.
|
Оксана Л.
|
8
|
|
|
+
|
|
|
20.
|
Сережа П.
|
15
|
|
|
+
|
|
|
21.
|
Эля Р.
|
8
|
|
|
+
|
|
|
22.
|
Саша С.
|
14
|
|
|
+
|
|
|
23.
|
Марина С.
|
10
|
|
|
+
|
|
|
24.
|
Сережа С.
|
17
|
|
+
|
|
|
|
25.
|
Миша С.
|
11
|
|
|
+
|
|
|
26.
|
Денис Ф.
|
21
|
|
+
|
|
|
|
27.
|
Женя Ф.
|
14
|
|
|
+
|
|
|
28.
|
Аня Ч.
|
9
|
|
|
+
|
|
Как видно из
таблицы, среди учащихся нет таких, кто полностью доверяет, либо не доверяет
своей интуиции: у 68% учащихся смешанный стиль, ближе к рациональному, а 32% -
больше преобладает интуиция, а не анализ и синтез.
С целью
определения уровня творчества была проведена методика 8.
Методика 8. Диагностика творческого мышления учащихся.
Ход
выполнения задания и необходимый материал.
I.
Разминочный
блок.
1. Дается
слово одуванчик. Необходимо из букв
этого слова составить как можно больше новых слов. (Время выполнения 3 минуты).
Два раза одну и туже букву в словах использовать нельзя. Высокий уровень
развития способности – 9 и более слов.
Средний
уровень – 7,8 слов.
Низкий уровень
– 6 и менее слов.
2. Детям
предлагается написать как можно больше предложений из пяти слов, в которых
каждое слово начинается с указанной буквы.
Р – И – С – Н
– К –
Для оценки
гибкости конструирования фраз подсчитывается количество верно составленных
предложений. Фраза должна обязательно выражать какой-либо смысл, а слова в
предложении должны быть согласованны по родам, числам и падежам. Добавлять
другие слова или предлоги не разрешается. Указанные буквы можно использовать в
качестве предлогов. (Время выполнения 5 минут).
Экран оценки результатов задания
|
Возраст детей
|
Уровни
|
|
высокий
|
средний
|
низкий
|
|
10-11 лет
|
4 и более
|
3
|
0-2
|
|
12 лет
|
5 и более
|
4
|
0-3
|
|
13 лет
|
6 и более
|
5
|
0-4
|
3. Из
трех скороговорок выбрать одну и как можно быстрее ее проговорить (устно).
Ткет ткач
ткани на платки Тане.
Топоры остры
до поры, до поры остры топоры.
Свинья
тупорылая весь двор перерыла, выросла на полрыла, до коры не доросла.
Быстро, чисто
– 2 балла.
С
погрешностями – 1 балл.
II.
Выберите тот ответ, который соответствовал бы
вашему поступку в предложенных ниже ситуациях.
1. Если
бы я строил детский городок, то
а) построил такой городок, которого нет нигде – 2
б) построил городок, по предложенному типовому проекту –
0
в) построил городок, который видел в кино, журналах
книгах – 1
2. Если
я приглашаю друзей на свой день рождения, то
а) пишу сценарий и готовлю сюрпризы – 2
б) говорю им время и надеюсь на родителей – 0
в) участвую в приготовлении блюд для гостей – 1
3. На
вопрос, поставленный учителем на уроке, я выбираю ответ:
а) простой – 0
б) сложный – 1
в) оригинальный – 2
4. Когда
я чем-то сильно очарован то:
а) пишу стихи – 2
б) просто любуюсь объектом очарования – 1
в) чувствую умиротворенность – 0
5. Когда
я провожу исследовательскую работу по моему любимому предмету, то:
а) читаю много дополнительной литературы – 2
б) подбираю материал попроще – 1
в) надеюсь на помощь учителя – 1
6. Для
меня в общении самое главное:
а) возможность узнавать яркое нешаблонное, неординарное –
2
б) поделится своими бедами с друзьями – 1
в) просто провести время – 0
7. Если
бы я стал ученым, то:
а) ездил часто за границу – 0
б) написал бы много полезных книг – 1
в) совершил бы открытия на пользу всему человечеству – 2
8. Из
трех тропинок, оказавшихся перед вами в лесу, вы выбрали ту:
а) которая вам удобна – 0
б) о которой вам рассказывали знакомые – 1
в) которая является неизвестной тропинкой – 2
9. Мне
хочется, чтобы в школе:
а) все учились в меру своих возможностей – 1
б) все были дружны – 0
в) узнавали как можно больше нового – 2
10. Произнесите
громко, отчетливо три скороговорки:
а) Жужжит над жимолостью жук. Зеленый на жуке кожух.
б) Два дровосека, два дроворуба, два дровокола дрова
рубили, дрова кололи, дрова секли.
в) Карл у Клары украл кораллы, а Клара у Карла украла
кларнет.
III.
Согласны ли вы со следующими высказываниями
великих. Обозначьте в карточке
следующими символами ваши ответы:
полностью
согласен – 0,
не согласны –
2,
не готов
оценить данное высказывание – 1.
11. Идеи могут
быть обезврежены только идеями (О. Бальзак).
12. Разум
человека сильнее его кулаков (Ф. Рабле).
13. Способности,
как и мускулы, растут при тренировке (И. Тимирязев).
14. Только
глупцы и покойники не меняют своих мнений (Д. Оруэлл).
15. Беда, коль
пироги начнет печь сапожник, а сапоги тачать пирожник. (И. Крылов).
16. Льстят тем,
кого боятся (А. Чехов).
17. Быть смелым
на слова легко, когда не собираются говорить всей правды (Р. Тагор).
18. Всякий
обладает достаточной силой, чтобы исполнить то, в чем он убежден (В. Гете).
19. Стыд перед
людьми – хорошее чувство, но лучше всего стыд перед самим собой (Л. Толстой).
20. Самый
счастливый человек тот, кто дает счастье наибольшему числу людей (Д. Дидро).
21. Величайшая
слабость ума заключается в недоверчивости к силам ума (В. Белинский).
IV.
Способность преобразовывать структуру объекта.
В первой
строке каждого вопроса есть пара слов, между которыми существует некая связь
или какое-то соотношение. Вы должны определить какая связь или какое
соотношение существует между этими двумя словами и выбрать из четырех
предложенных ответов пару слов, между которыми существует та же связь или то же
соотношение. (Правильный ответ – 2 балла).
22. МОРЕ –
БАССЕЙН
1)
река – труба
2)
река – душ
3)
река – лука
4)
река – вода
23. ВОЗРОЖДЕНИЕ
– ПОБЕДИТЕЛЬ
1)
подъем – высота
2)
подъем – учитель
3)
подъем – гора
4)
подъем – спуск
24. ПЧЕЛА – МЕД
1)
собака – шерсть
2)
кабан – мясо
3)
коза – молоко
4)
лошадь – хвост
Представлена
исходная пара слов, которые назодятся в определенном соотношении, и пять других
слов, из которых только одно находится в таком же отношении к исходному слову
(правильный выбор – 2 балла).
25. БОЛЬНИЦА –
ЛЕЧЕНИЕ
Институт
а) профессор
б) преподавание
в) обучение
г) учреждение
д) студент
26. МУХА –
ПАУТИНА
Рыба
а) паук
б) треска
в) сеть
г) удочка
д) плавание
27. СМЕХ –
ПЕЧАЛЬНЫЙ
Горе
а) легкий
б) клоун
в) апатия
г) радостный
д) мрачный
V.
Словесные ассоциативные способности.
Найдите выход
из ситуации:
28. Вас избрали
губернатором области. Ваши первоочередные действия.
29. Вы купались
в реке. У вас похитили одежду. Вам нужно найти выход из положения.
30. Вы
оказались в африканском племени аборигенов. Ваши действия?
Экспериментатор оценивает ответ следующим образом:
отсутствие
ответа – 0
тривиальный
ответ – 1
оригинальный
ответ – 2.
Перечислите
как можно больше способов применения каждого предмета.
31. Велосипедная
спица
32. Зубная
щетка.
33. Полиэтиленовая
бутылка.
VI.
(контрольный
блок).
Да – 2 балла,
трудно сказать – 1, нет – 0.
34. Мне приятно
ощущать чувство новизны.
35. Мне удается
представить то, чего не бывает в действительности.
36. Хорошо
ориентируюсь в трудных ситуациях.
37. Часто
ощущаю прилив творческих сил.
38. Могу
аргументировать свое пристрастие к чему-либо.
39. Оригинальные
идеи часто посещают меня.
40. Умею
разграничить в сложных задачах главное и второстепенное.
41. Всегда рад
услышать оценку своего труда от окружающих.
42. Я научился
распознавать причины своих неудач.
43. Мне часто
не хватает школьного учебного материала для удовлетворения моих познавательных
потребностей.
44. Я верю в
свои способности и возможности.
Обработка
данных.
Более 67%
выполненных заданий с баллом 2 – высокий уровень творчества; не менее 50%
выполненных заданий с баллом 2 – средний уровень творчества.
Результаты
выполнения методики представлены в таблице 8.
Таблица 8.
|
№
|
Учащиеся
|
Количество
заданий выполненных с высшим баллом, %
|
Уровень
творчества
|
|
низкий
|
средний
|
высокий
|
|
1.
|
Павел А.
|
49
|
+
|
|
|
|
2.
|
Андрей Б.
|
53
|
|
+
|
|
|
3.
|
Яна Б.
|
64
|
|
+
|
|
|
4.
|
Рома Б.
|
64
|
|
+
|
|
|
5.
|
Сережа Б.
|
62
|
|
+
|
|
|
6.
|
Аня Г.
|
45
|
+
|
|
|
|
7.
|
Игорь Г.
|
43
|
+
|
|
|
|
8.
|
Костя Е.
|
57
|
|
+
|
|
|
9.
|
Аня И.
|
51
|
|
+
|
|
|
10.
|
Вова К.
|
45
|
+
|
|
|
|
11.
|
Юля К.
|
64
|
|
+
|
|
|
12.
|
Оксана К.
|
85
|
|
|
+
|
|
13.
|
Ксения К.
|
66
|
|
+
|
|
|
14.
|
Георгий К.
|
90
|
|
|
+
|
|
15.
|
Надя К.
|
55
|
|
+
|
|
|
16.
|
Маша К.
|
66
|
|
+
|
|
|
17.
|
Катя Л.
|
43
|
+
|
|
|
|
18.
|
Дима Л.
|
38
|
+
|
|
|
|
19.
|
Оксана Л.
|
62
|
|
+
|
|
|
20.
|
Сережа П.
|
49
|
+
|
|
|
|
21.
|
Эля Р.
|
55
|
|
+
|
|
|
22.
|
Саша С.
|
53
|
|
+
|
|
|
23.
|
Марина С.
|
66
|
|
+
|
|
|
24.
|
Сережа С.
|
38
|
+
|
|
|
|
25.
|
Миша С.
|
47
|
+
|
|
|
|
26.
|
Денис Ф.
|
43
|
+
|
|
|
|
27.
|
Женя Ф.
|
49
|
+
|
|
|
|
28.
|
Аня Ч.
|
62
|
|
+
|
|
Из таблицы
видно, что только 7% учащихся имеют высокий уровень творчества; 39% - низкий и
54% - средний.
С целью
определения уровня сформированности интеллектуальных умений, была проведена
методика 9.
Методика 9. Сформированность интеллектуальных умений.
Ход
выполнения задания.
Данная
методика предлагается учителям для оценки учеников и может быть использована
учениками для самоанализа уровня сформированности у них интеллектуальных умений
по предметам, наиболее и наименее трудным для усвоения.
Предполагаемые
баллы имеют следующее описание:
2 – умение ярко выражено;
1 – умение имеет место;
0 – умение не сформировано.
Следует обвести
балл, соответствующий мнению испытуемого.
Необходимый
материал.
I.
Ученик умеет слушать:
-
объяснение учителя, не опирающиеся на средства
наглядности 2 1 0
-
объяснения учителя, опирающиеся на средства
наглядности 2 1 0
-
вопросы учителя к средствам наглядности 2 1 0
-
вопросы учителя о связях между явлениями,
представленными в наглядной форме 2 1 0
-
ответы товарищей во время опроса 2 1 0
-
оценивать свой ответ, то есть слушать самого
себя 2 1 0.
II.
Ученик умеет работать с наглядностью:
-
формулировать вопросы к иллюстрируемым
фактам 2 1 0
-
схематизировать текст, представить его в
таблице, схеме 2 1 0
-
самостоятельно изготовить пособие на основании
чтения 2 1 0
-
объяснить, когда наглядное пособие может быть
использовано 2 1 0
-
давать наглядное и логическое объяснение
материала на основании самостоятельного изготовленного наглядного пособия 2 1 0
-
формировать вопросы к наглядным пособиям и
оценивать их 2 1 0.
III.
Умеет работать с текстом:
-
излагать текст своими словами 2 1 0
-
разделять текст на логические части и составлять
план 2 1 0
-
систематизировать учебный материал 2 1 0
-
делать вступление к своему сообщению 2 1 0
-
строить логически законченный рассказ 2 1 0
-
раскрывать материал в сравнении 2 1 0.
IV.
Умеет оперировать знаниями:
-
пользоваться справочной литературой 2 1 0
-
на основании ряда изложенных фактов делать
обобщения 2 1 0
-
формулировать познавательную задачу,
содержащуюся в тексте 2 1 0
-
высказывать собственное отношение к фактам и
событиям 2 1 0
-
самостоятельно формулировать вопросы 2 1 0
-
сопоставлять новый материал с уже известными
фактами 2 1 0.
V.
Умеет проявлять творческую самостоятельность:
-
при решении задач, предлагаемых учителем на
уроке 2 1 0
-
при решении учебных задач, выполняя домашнее
задание 2 1 0
-
проводя анализ, сравнения, сопоставления 2 1 0
-
делая выводы
2 1 0
-
делая обобщения на основании ряда фактов 2 1 0.
VI.
Умеет применять знания на практике:
-
формулируя гипотезу в исследовательском
поиске 2 1 0
-
намечая пути ее проверки 2 1 0
-
проводя элементарное исследование с привлечением
дополнительного материала по этой теме
2 1 0
-
осуществляя перенос знаний на рассмотрение
текущих событий 2 1 0
-
применяя знания в общественной работе 2 1 0.
Обработка
данных.
Подсчитывается
общее число баллов. Если общая оценка 50 баллов и более – высокий уровень
сформированности интеллектуальных умений; оценка 35-49 – средний уровень.
Данные по
выполнению задания приведены в таблице 9.
Таблица 9.
|
№
|
Учащиеся
|
Общий балл
|
Уровень
сформированности интеллектуальных умений
|
|
низкий
|
средний
|
высокий
|
|
1.
|
Павел А.
|
19
|
+
|
|
|
|
2.
|
Андрей Б.
|
61
|
|
|
+
|
|
3.
|
Яна Б.
|
44
|
|
+
|
|
|
4.
|
Рома Б.
|
58
|
|
|
+
|
|
5.
|
Сережа Б.
|
58
|
|
|
+
|
|
6.
|
Аня Г.
|
40
|
|
+
|
|
|
7.
|
Игорь Г.
|
30
|
+
|
|
|
|
8.
|
Костя Е.
|
62
|
|
|
+
|
|
9.
|
Аня И.
|
45
|
|
+
|
|
|
10.
|
Вова К.
|
48
|
|
+
|
|
|
11.
|
Юля К.
|
60
|
|
|
+
|
|
12.
|
Оксана К.
|
63
|
|
|
+
|
|
13.
|
Ксения К.
|
49
|
|
+
|
|
|
14.
|
Георгий К.
|
65
|
|
|
+
|
|
15.
|
Надя К.
|
43
|
|
+
|
|
|
16.
|
Маша К.
|
45
|
|
+
|
|
|
17.
|
Катя Л.
|
34
|
+
|
|
|
|
18.
|
Дима Л.
|
34
|
+
|
|
|
|
19.
|
Оксана Л.
|
44
|
|
+
|
|
|
20.
|
Сережа П.
|
43
|
|
+
|
|
|
21.
|
Эля Р.
|
43
|
|
+
|
|
|
22.
|
Саша С.
|
32
|
+
|
|
|
|
23.
|
Марина С.
|
63
|
|
|
+
|
|
24.
|
Сережа С.
|
40
|
|
+
|
|
|
25.
|
Миша С.
|
42
|
|
+
|
|
|
26.
|
Денис Ф.
|
33
|
+
|
|
|
|
27.
|
Женя Ф.
|
47
|
|
+
|
|
|
28.
|
Аня Ч.
|
49
|
|
+
|
|
Как видно из
таблицы, у 29% учащихся класса высокий уровень сформированности
интеллектуальных умений, у 21% - низкий и у 50% - средний.
Констатирующая
серия эксперимента показала следующий результат (данные по умению мыслить
совпали с данными таблицы 9): 29% учащихся имеют высокий уровень умения
мыслить, 21% - низкий и 50% - средний.
Целью
обучающей серии эксперимента стала организация интеллектуального развития
школьников посредством проблемного обучения.
Обучающая
серия была проведена на материале геометрии «Подобие и площади фигур». На
каждом уроке особое внимание уделялось решению задач проблемного характера.
После
обучающей серии эксперимента, с целью выяснения, насколько эффективно была
организованна работа по развитию интеллекта учащихся, была проведена
контрольная серия эксперимента, результаты которой представлены на диаграмме.
Из диаграммы
видно, что изменения произошли незначительные, но и они говорят об
эффективности проблемного обучения для интеллектуального развития.
2.2. Организация уроков математики с
элементами проблемного обучения.
Курс геометрии
своей строгостью и логической последовательностью создает большие возможности
для проблемного обучения. Отдельные темы курса настолько связанны между собою,
что сознательное усвоение одной из них создает условия для предвидения
проблемы, которые возникают при изучении последующих.
Основой
проблемного обучения на уроках геометрии является знакомство учащихся с новыми
геометрическими фактами путем создания проблемных ситуаций, способствующих
выдвижению гипотезы о свойствах рассматриваемых объектов и с последующим
поиском доказательства справедливости выдвинутого предположения.
Наведению
ученика на догадку может способствовать удачно подобранная система
подготовительных упражнений, включающих в себя выполнение практических работ по
измерению, построению, моделированию, рассмотрению наглядных пособий и
чертежей, проведению эксперимента.
Во время
педагогической практики у меня была возможность разнообразить уроки элементами
проблемного обучения.
Соотношение между тригонометрическими функциями одного и того же аргумента.
Если учащиеся
убеждены в существовании неизвестного математического объекта или неизвестных
математических соотношений, то, естественно, возникает интерес к поиску этих
объектов и соотношений – их открытию.
Целесообразно
создать проблемную ситуацию, мотивирующую обязательное существование каких-то
соотношений между двумя тригонометрическими функциями одного и того же
аргумента. Вместе с тем получим ситуацию, мотивирующую тему и цель урока:
открыть и изучить эти соотношения.
Краткое
содержание проблемной беседы:
Если нам
известно значение одной какой-либо тригонометрической функции, острого угла, то
можно найти значения любой иной тригонометрической функции того же угла. Как,
например, зная, что sin a=3/5, найти cos a, tg a
и т.д.?
Учащиеся
указывают два приема:
1)
найти по таблицам угол a и затем по тем же
таблицам cos a, tg a и
т.д.
2)
можно построить угол a и измерить стороны
полученного прямоугольного треугольника и т.д.
А нельзя ли
решить задачу, если нет возможности пользоваться таблицами и построениями?
Здесь учащиеся
испытывают затруднение. В этот момент уже возникает проблемная ситуация,
мотивирующая постановку темы и цели урока: вывести такие формулы, которые
позволяют решить поставленную задачу.
Поисковую
проблемную ситуацию можно создать с помощью таких вспомогательных задач.
1)
Катет прямоугольного треугольника равен 20 см.,
гипотенуза 25 см. Найти второй катет и его отношение к гипотенузе. Найти
отношение первого катета к гипотенузе. Найти сумму квадратов обоих отношений.
2)
Отношение одного катета к гипотенузе равно 4/5. Найти
отношение второго катета к гипотенузе. Найти сумму квадратов обоих отношений.
3)
Синус острого угла равен 4/5.найти косинус этого угла.
4)
Отношение одного катета к гипотенузе равно m, а второго – n. Докажите, что сумма
квадратов этих отношений равна 1.
Такое (или
сходное) задание способствует успешному самостоятельному поиску и открытию
искомого отношения.
В более
подготовленном классе достаточно (для создания поисковой ситуации) предложить
учащимся решить при помощи теоремы Пифагора задачу: «По данному синусу угла a (sin a=m/n), найти его косинус». В
процессе решения этой задачи и будет открыто искомое соотношение.
Теорема об отрезках хорд, пересекающихся внутри круга.


 Перед изучением темы учащимися
предлагается дома решить следующую задачу:
Перед изучением темы учащимися
предлагается дома решить следующую задачу:
Хорда AB, пересеклась с хордой CD в точке О, делится на
отрезки АО=45 мм. и ОВ=30 мм. определить отрезок CD, если OD=90 мм.
Урок
начинается с проверки выполнения домашнего задания. Выясняется, что большинство
учеников справились с работой, притом различными способами.
Одни построили
отрезок АВ=75 мм, отметили на нем точку О и отложили отрезок OD=90 мм. по трем точкам A, B, D построили окружность.
Точка С была найдена как точка пересечения прямой OD с этой окружностью.
Другие
построили круг произвольного радиуса, в нем хорду АВ=75 мм и на последней точку
О. На окружности отметили точку D
так, что OD=90 мм.
Точка С была найдена как точка пересечения прямой OD с окружностью.
Третьи
построили чертеж и нашли отрезок СО из подобия треугольников AOC и BOD.
Каждый способ
решения задачи ученики объясняли по своим же чертежам. Последний способ решения
задачи отмечается учителем как самый рациональный.
Учеников очень
удивило то, что, несмотря на произвольность угла пересечения хорд (в первом
случае), радиуса круга (во втором случае) и различия способов решения задачи,
они получили один и тот же результат: СО=15 мм. Это убедило их в существовании
определенной зависимости между отрезками пересекающихся в круге хорд. Еще раз
обратившись к третьему случаю решения задачи, ученики сформулировали проблему:
найти свойство отрезков пересекающихся хорд. Затем учитель называет тему урока
и записывает ее. Построив чертеж, ученики составили пропорцию из отношения
сходственных сторон подобных треугольников. Используя основное свойство
пропорции, они дали формулировку теоремы.
Таким образом,
проблемная ситуация возникла в результате рассмотрения способов решения
конкретной задачи.
Тема урока
заранее не объявляется, а вытекает из проблемной ситуации. Она принимается
учащимися как своя, поскольку ими выстрадана, заработана в процессе умственной
деятельности. Так, тема урока становится проблемой, разрешение которой увлекает
учащихся.
Еще один
вариант создания проблемной ситуации.
Учитель
предлагает классу лабораторную работу: каждый учащийся строит в тетради
окружность и две-три пересекающиеся в одной точке внутри окружности хорды,
измеряет миллиметровой линейкой (с точностью до 1 мм) отрезки хорд, находит
произведение длин отрезков каждой хорды и сравнивает эти произведения.
Учащиеся с
интересом замечают, что все произведения оказываются приблизительно равными.
Учитель
отличает, что обнаруженная закономерность не случайна, т.к. имеет место
соответствующая теорема. Формулировку теоремы могут дать сами учащиеся.
Сумма внутренних углов выпуклого многоугольника.
Для создания
поисковой проблемной ситуации можно использовать метод неполной индукции в
сочетании с методом нацеливающих задач.
Вот серия
упражнений, которые должны выполнить учащиеся, чтобы самостоятельно открыть
формулу, выражающую сумму всех внутренних углов выпуклого многоугольника через
число n его сторон.
Внутренняя точка выпуклого четырехугольника соединена с
его вершинами. Сколько получилось треугольников и какова сумма углов всех
треугольников? На сколько эта сумма больше суммы всех внутренних углов
четырехугольника?
Решите такую же задачу для выпуклого пятиугольника.
Найдите сумму внутренних углов: а) четырехугольника; б) пятиугольника.
Вычислить сумму внутренних углов выпуклого стоугольника.
После
успешного выполнения учащимися этих упражнений смело предлагаем им решить
задачу 4) для произвольного выпуклого n-угольника.
Можно
построить вспомогательную серию задач, ведущую учащихся по иному пути вывода
формулы: п-угольник разбивается на треугольники диагоналями, выходящими
из одной вершины. В этом случае необходимо индуктивным путем подвести учащихся
к самостоятельному открытию закономерности: число треугольников разбиения равно
n –
2.
Если учащиеся
самостоятельно выведут формулу S=180°(n-2) одним способом, то они смогут вывести ее
(без вспомогательных упражнений) другим.
Длина окружности.
Учащиеся 6
класса получают домашнее задание: каждый измеряет, пользуясь ниткой и
миллиметровой линейкой, длину С окружности и диаметр D какого-либо круглого тела и вычисляет
отношение первого результата ко второму.
Несколько
учащихся вызываются к доске и вписывают в начерченную там таблицу результаты
своих измерений. Можно поручить одному-двум учащимся аккуратно начертить такую
таблицу для всего класса и уже заполненную принести на урок.
Изучая на
уроке эту таблицу, учащиеся открывают закономерность: отношение длины
окружности к ее диаметру остается почти постоянным. Учителю остается добавить:
в математике доказано, что это отношение строго постоянно и может быть
вычислено с любой точностью; до 0.01 равно 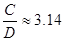 . Каждый учащийся получает возможность оценить, насколько
точно он провел измерения (сопоставляя это число со своим результатом).
. Каждый учащийся получает возможность оценить, насколько
точно он провел измерения (сопоставляя это число со своим результатом).
В таблице
можно отразить тот факт, что с увеличением
диаметра в n раз
(nÎN) длина окружности
увеличивается также в n
раз (специально раздаем учащимся круги, диаметры которых равны 1, 2, 3 дм.).
Таблица покажет, что длина окружности с диаметром 1дм приближенно равна 3.14
дм, и что остальные окружности имеют длину соответственно в 2 и 3 раза большую.
Перед домашним заданием (лабораторной работой) полезно
создать проблемную ситуацию, мотивирующую необходимость научиться вычислять
длину окружности по известному диаметру (радиусу) или диаметр (радиус)
окружности по известной длине. С этой целью можно использовать, например, такие
проблемные задачи:
1)
Нужно построить цилиндрическую цистерну диаметром в 20
м и высотой в 8 м. Сколько квадратных метров содержит боковая поверхность этой
цистерны?
Это
потребуется знать при определении количества строительных материалов, которые
необходимы для постройки боковых стенок цистерны. Может возникнуть, например,
такая частная проблема: сколько эмалевой краски потребуется для покраски
боковой поверхности цистерны, если на каждый квадратный метр расходуется 50 г?
Учитель с
помощью развертки цилиндра легко убеждает учащихся в том, что для нахождения
его боковой поверхности нужно длину окружности умножить на высоту. Возникает
задача: как по известному диаметру окружности (20 м) найти ее длину? ( Ведь мы
не можем «развернуть» цистерну).
2)
Нужно построить цилиндрическую цистерну высотой 5 м.
Каким должен быть поперечник (диаметр) цистерны, чтобы для обшивки ее боковой
поверхности хватило 785 кв. м. железа?
С помощью
учителя учащиеся убеждаются в том, что для решения этой задачи необходимо
умение находить диаметр окружности по известной длине (785:5=157 м).
После изучения
нового материала (формула длины окружности) учащиеся доводят решение проблемных
задач до конца.
Развернутый угол.
На доске дан
чертеж.
Учитель обращается к классу с
вопросами:
1.
Какие фигуры изображены на доске?
(лучи, отрезки, углы)
2.
Сколько лучей изображено на (1)?
Сколько на (2)?
3.
Сколько углов построено на рисунке (4)?
Сколько всего углов на доске?
Предположительный ответ на
последний вопрос – 8 углов.
Учитель: «Нет,
ребята, здесь не 8, а гораздо больше углов! Какие же углы вы сосчитали? Чтобы
найти потерянные вами углы, вспомните, как строится угол («…из точки провести
два луча»), и постарайтесь увидеть на доске все новые углы».
По завершению работы учащиеся дают
определение. Угол называется развернутым, если его стороны являются
дополнительными полупрямыми одной прямой.
2.3. Подборка заданий проблемного характера.
При выполнении
дипломной работы мы поставили перед собой ряд задач. Одна из них состоит в
подборке заданий проблемного характера.
Перед
рассмотрением проблемных задач кратко остановимся на некоторых общих вопросах и
задачах.
Математической
задачей называют требование осуществить некоторую математическую деятельность в
указанных условиях. По роли, которую играют учебные задачи, их делят на:
-
репродуктивные;
-
задачи с известным алгоритмом;
-
проблемные.
Репродуктивные
задачи ставят своей целью припомнить то, что учащиеся узнали на предыдущих
занятиях. Обычно их предлагают в виде вопросов, например: «Как формулируется
теорема Пифагора?», «Чему равна сумма синусов двух углов?». Они важны потому,
что без знания теоретического материала нельзя приступать к решению
поставленной задачи. Задачи репродуктивного характера в некоторой мере помогают
учащимся систематизировать пройденное. Однако, укрепляя память, они совершенно
не развивают мышление, поэтому не могут считаться основными.
В задачах
второй группы речь идет об использовании учащимися полученных ранее знаний. При
этом общий план решения поставленной задачи ясен, остается только выбрать из
числа изученных теорем или формул пригодные для достижения намеченной цели.
Принципиальных трудностей при решении задач второй группы обычно не возникает.
Они помогают лучше разобраться в изученном, систематизировать пройденное. Таких
задач на уроке математики большинство. Однако задачи с известными алгоритмами
не знакомят нас с новыми математическими фактами, с приемами математической
деятельности, не способствуют математическому развитию.
Проблемная
задача характерна тем, что алгоритм ее решения до начала решения неизвестен,
трудно даже установить, достаточно ли знаний и умений учащегося для выполнения
задания. Главная задача – открыть способ решения и убедиться в его пригодности.
Следует иметь в виду, что определить, является ли данная задача проблемной или
нет, можно только относительно конкретного школьника, только с учетом его
знаний и умений в момент постановки задачи.
Д.З.Кнебельман
называет следующие особенности проблемных задач:
а) задача
должна вызывать интерес своей необычностью, неожиданностью, нестандартностью.
Информация особенно привлекает учащихся, если она содержит противоречивость,
хотя бы кажущуюся. Проблемное задание должно вызвать удивление, создать
эмоциональный фон;
б) проблемные
задачи обязательно должны содержать посильное познавательное или техническое
затруднение. Казалось бы, видимому решению «мешает» досадное затруднение, и
неизбежно возникает всплеск мыслительной активности;
в) проблемное
задание предусматривает элементы исследования, поиск различных способов его
выполнения, их сравнения. Удовлетворив познавательную пытливость учащихся,
задачи эти должны пополнить багаж их знаний новыми методами, новой информацией
и т. п.
Важно
отметить: ни слишком легкая, ни слишком трудная для ученика задача не может
вызвать активную мыслительную деятельность, то есть стать для школьника
проблемной. Вызвать проблемную ситуацию. Легкую задачу ученик решит на основе
так называемого репродуктивного мышления, которое предполагает прямое, не
требующее поиска применение уже имеющихся знаний. Слишком трудная задача так же
не вызовет у ученика мыслительной активности. Если даже он и сделает ряд
попыток решить такую задачу, то очень скоро, убедившись в их малой
эффективности, займет позицию пассивного слушателя, ожидающего от других
готового решения.
Выбор
проблемной задачи зависит от наличия у учащихся исходного минимума знаний или
возможности за относительно короткий срок
до постановки проблемы сообщить учащимся необходимые для
самостоятельного решения сведения. Вместе с тем надо помнить, что эти знания должны
служить опорой для поисков пути решения, а не «наводить», не подсказывать этот
путь, иначе задача перестанет быть проблемной.
Итак, задача
становится проблемной, если она удовлетворяет следующим требованиям:
1)
представляет познавательную трудность, т. е. Требует
размышлений над изучаемой проблемой;
2)
вызывает познавательный интерес;
3)
опирается на прежний опыт и знания учащихся.
К проблемным задачам относятся
задачи, в которых условие либо противоречиво, либо решение невозможно при
конкретных данных, либо они имеют еще какой-то «изъян», сводящий на нет саму
задачу, делающий ее неверной по сути. Такие задач учат думать, сомневаться,
искать, находить.
Задача 1. Докажите, что
четырехугольник, у которого две стороны параллельны, а две другие равны – параллелограмм.
Ответ:
утверждение задачи неверно. Это может быть и равнобокая трапеция.
Задача 2. Большая сторона треугольника
ABC, равная 10 см, лежит против угла 45°.
Найдите радиус описанной около
треугольника ABC
окружности.
Ответ: нет необходимости
применять формулу 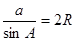 , т. к. задача не имеет смысла. Действительно, против большей
стороны треугольника лежит больший угол, а он должен превышать 60°
(иначе сумма углов треугольника будет меньше, чем 180°).
, т. к. задача не имеет смысла. Действительно, против большей
стороны треугольника лежит больший угол, а он должен превышать 60°
(иначе сумма углов треугольника будет меньше, чем 180°).
Задача 3. Решите треугольник ABC, если AB:AC:BC=1:3:6,а периметр равен 20 см,
угол B равен 110°.

Дано: DABC
AB:AC:BC=1:3:6
P=20 см,
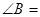
110°
Найти:
AB, BC, AC, 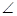 A,
A,  C.
C.
Решение:
1.
По следствию теоремы синусов в треугольнике против
большего угла лежит большая сторона.
2.
В ABC
есть тупой угол Þ
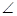 B -
больший.
B -
больший.
3.
Из п. 1, 2 Þ - большая.
4.
По условию AB:AC:BC=1:3:6 Þ BC - большая сторона.
5.
Из п. 3, 4 Þ противоречие Þ сформулированная
задача имеет нереальные условия.
Если эту задачу начать решать,
предварительно не проанализировав ее условие, то можно получть неверное, но
кажущееся правильным решение.
В этой задаче надо не только разбить
условие задачи на данные и требования, но и установить связи между данными
задачи, определить, нет ли противоречий в условии задачи.
Такие задачи относятся к проблемным
потому, что содержат в себе противоречивость, тем самым вызывая удивление и
интерес учащихся.
Задача 4. Разделите данный треугольник на три
равновеликие части прямыми, проходящими через одну вершину.
Решение:
1) AD=DE=EC.
2) 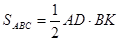 .
.
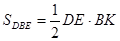 .
.
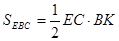 .
.
3) п.1, п.2 Þ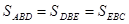 .
.
4) п.3 Þ BD и BE – искомые прямые, делящие
треугольник на три равные части.
Задача 5.
Разделите параллелограмм на три равновеликие части прямыми, проходящими через
одну вершину.
Решение:
1) BE=EK=KC.
2) CL=LM=MD.
3) 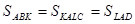 (см предыдущую
задачу).
(см предыдущую
задачу).
4) п.3
Þ
прямые AK и AL разделяют
параллелограмм на три равновеликие части.
Задача 6.
Докажите, что любой треугольник можно разрезать на несколько равнобедренных
треугольников.
Доказательство:
Хоть одна из
высот треугольника находится внутри треугольника. Такая высота делит
треугольник на два прямоугольных треугольника. Таким образом, треугольник можно
разделить на любое число n³2
прямоугольных треугольников. А каждый прямоугольный треугольник делится
медианой, проведенной к гипотенузе, на два равновеликих треугольника.
Задача 7. Докажите, что пятиугольник и
можно разрезать на 3 трапеции.

Доказательство:
1)


Проводим
BKúïAE, ENúïDC
2)
 BKÇEN=0
BKÇEN=0
3)
ОМúïВС
4)
 АВОЕ, ОМDE, ОВСМ – трапеции.
АВОЕ, ОМDE, ОВСМ – трапеции.
Так как все
элементы построения осуществимы, утверждение о возможности построения верно.
Задача 8. Как через вершину выпуклого
четырехугольника провести прямую, которая разделяет четырехугольник на две
равные части?


Решение:



Если точка О – середина диагонали BD, то ломаная АОС делит
четырехугольник на две равновеликие части. Если провести ОМúïАС, то SABCM=SAMD.
Задача
9. Как через данную точку на основании треугольника провести прямую,
которая разделяет треугольник на две равновеликие части?
Решение:



Медиана ААо делит треугольник на две
равновеликие части.


Если провести АХúïМАо, то SABXM=SMXC.
Задача 10. Как через данную точку на
основании треугольника провести две прямые, которые, разделяют треугольник на
три равновеликие части?
Решение:





Если AD=DE=EC и TDúïBM, KEúïBM, то прямые МТ и МК – искомые.
Задача 11. В треугольнике АВС дано,
что 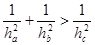 . Каким должен быть угол С: тупым или острым?
. Каким должен быть угол С: тупым или острым?
Решение:
1)
S-площадь
DАВС.
2)
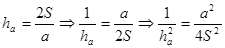 ,
,
3)

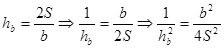 ,
,
4)
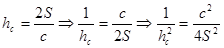 ,
,
5)
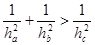 (по условию)
(по условию)
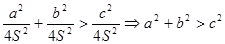
6)
по теореме косинусов:
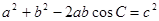
7)
п.5, п.6 Þ 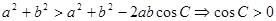 .
.
8)
п.7Þ ÐС
– острый.
Ответ: ÐС – острый.
Задача 12. В треугольнике АВС угол А в
два раза больше угла В. доказать, что 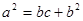 .
.
Дано:


DАВС
ÐА=2ÐВ
Доказать:

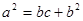
.
Доказательство:
1)
По теореме косинусов
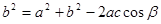 .
.
2)
По теореме синусов:
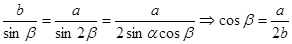 .
.
3)
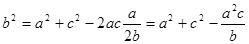 ,
,
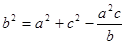 ,
,
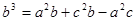 ,
,
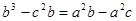 ,
,
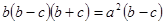 .
.
4)
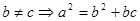 .
.
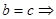 ÐВ=ÐС ÞÐВ+ÐС=ÐА ÞÐА=90°Þ
ÐВ=ÐС ÞÐВ+ÐС=ÐА ÞÐА=90°Þ
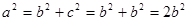 .
.
Ч.т.д.
Задача 13. Прямая проходящая через
вершину прямого угла треугольника, образует с меньшим катетом угол 30° и
пересекает гипотенузу в точке, которая делит ее в отношении 1:2. Найти длину
гипотенузы, если длина меньшего катета равна Ö3.
Дано:

DАВС (ÐС – прямой),
ÐDCB=30°,
BD:DA=1:2,

BC=Ö3
Найти : АВ.
Решение:
1)
ÐА=a Þ
ÐВ=90°-a (по
теореме о сумме углов в треугольнике),
0°<a<45°
2)
Из DACD и DBCD
По теореме синусов:
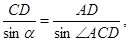
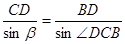 .
.
3)
П.2 Þ 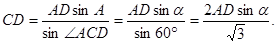
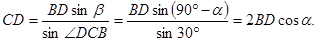
4)
П.3.Þ 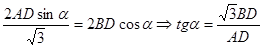 .
.
5)
П.4.Þ 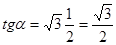 .
.
6)
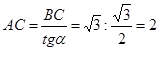
7)
Из DАВС по теореме Пифагора

Ответ: Ö7
Задача 14. Три хорды окружности
радиуса R образуют
вписанный в эту окружность треугольник. Найти длину третьей хорды, если две
другие равны RÖ3 и R/2.


Дано:

DАВС –
вписан в окружность,
ВС=RÖ3,
СА=R/2.
Найти: АВ.
Решение:
1)
Найдем синус и косинус углов a и b.
По теореме синусов:
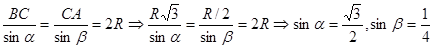
2)
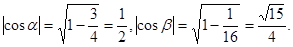
3)
g=180°-a-b (по теореме о сумме углов треугольника)
4)
sing=sin(180°-(a+b))=sin(a+b).
Углы a и b могут быть острыми либо
один из них тупой. Рассмотрим все случаи.
5)
a, b - острые:
cosa=1/2; cosb=Ö15/4,
sing=sinacosb+cosasinb=(Ö3/2)×(Ö15/4)+1/8=(3Ö5+1)/8,
По теореме синусов:
АВ=2R sing=R(3Ö5+1)/8.
6)
a-тупой, b-острый.
cosa=-1/2, cosb=Ö15/4,
sing=(3Ö5-1)/8,
AB=R(3Ö5+1)/8.
7)
a-острый, b-тупой.
cosa=1/2 ,cosb= -Ö15/4,
sing=(-3Ö5+1)/8<0, а это невозможно
для внутреннего угла треугольника.
Возможные
случаи представлены на рисунках.
Задача 15. Показать что во всяком
прямоугольном треугольнике сумма диаметров описанной окружности и вписанной
окружностей равна сумме его катетов.
 Дано:
Дано:

DАВС (ÐС-прямой).
Доказать:


2R+2r=a+b, где R – радиус описанной
окружности,


а
r – радиус вписанной
окружности.
Доказательство:
По свойству
отрезков касательных имеем
a+b=AK+KL=CM+MB=AL+r+r+LB=2r+AB=2r+c=2r+2R.
Ч.т.д.
Задача 16. В треугольник АВС вписана
окружность. К окружности в точке Е проведена касательная, пересекающая сторону
АВ в точке К, а сторону ВС – в точке М. Найти периметр треугольника КВМ, если
стороны треугольника АВС равны а,b,c.

Дано:

DАВС
описан около окружности,

КМ
– касательная.
Найти:
РКВМ.
Решение:
1)
РКВМ=ВК+КМ+МВ.
2)
По свойству отрезков касательных
КР=РЕ,
МЕ=ML,
BP=BL,
AP=AN,
CL=CN.
3)
П.1, п.2.ÞРКВМ=ВК+КЕ+ЕМ+МВ=(ВК+КР)+(ML+MB)=BP+LB=2BP.
4)
a+c=AB+BC=BP+PA+BL+LC=(BP+BL)+(PA+LC)=2BP+9AN=CN)=2BP+b.
5)
П.3, п.4. Þ a+c=PKBM+b Þ PKBM=a+c-b.
Ответ: a+c-b.
Задача
17. В равнобедренный треугольник АВС с основание АС вписана окружность.
Прямая, параллельная стороне АВ и касающаяся окружности, пересекает сторону АС
в такой точке М, для которой МС=2/5АС. Найти радиус окружности, если периметр
треугольника АВС равен 20.

 Дано:
Дано:
DАВС (АВ=ВС),

МКúçАВ,
точка LÎокружности,
МС=2/5АС,

РАВС=20.
Найти: r.
Решение.
1)
r=OH
2)
DMKC
DАВС
(по углам) Þ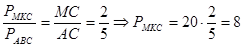 .
.
3)
С другой стороны, по свойству отрезков касательных
РМКС=MC+ML+LK+KC=MC+HM+KQ+KC=CH+CQ=2CH=AC.
4)
П.3Þ АС=8.
5)
АВ=ВС=1/2(20-8)=6.
6)
Из DАВН по теореме Пифагора
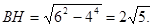
7)
в DАВН АО-биссектриса Þ
по свойству биссектрисы 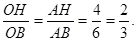
8)
п.7.Þ ОН=2/5 ВН=4Ö5/5.
Ответ: (4Ö5)/5.
Задача 18. Медиана BK и биссектриса CL треугольника ABC пересекаются в точке .доказать
равенство 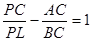 .
.

Доказательство:
1.

 LMúçBK.
LMúçBK.
2.

DALM DABK Þ

.
3.
DPCK
DLCM Þ
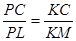
.
4.
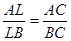
(по свойству
биссектрисы).
5.
п.2, п.4 Þ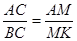 .
.
6.
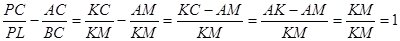 .
.
Ч.т.д.
Задача 19. В треугольнике ABC известно, что угол A в два раза больше угла C, сторона BC на 2 см больше стороны AB а AC=5 см.
Найти AB и BC.
Дано:

 DABC,
DABC,
ÐA=2ÐC,
 BC=AB+2 см,
BC=AB+2 см,
AC=5 см.

Найти: AB, BC.
Решение:
1)
AD – биссектриса
угла BAC.
2)
П.1Þ ÐBAD=ÐDAC=ÐACD Þ DADC – равнобедренный.
3)
Обозначим AB=x, AD=DC=y.
4)
П.3 Þ BC=x+2, BD=x+2-y.
5)
DABD
DABC (по углам) Þ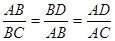 ,
, 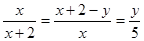 .
.
6)
x
и y найдем из системы

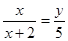 , 5x=xy+2y,
, 5x=xy+2y,
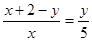 ; 5x+10-5y=xy;
; 5x+10-5y=xy;
5y-10=2y;
y=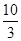 ,
,
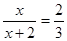 ,
,
x=4.
7)
AB=4см,
BC=6см.
Ответ: 4 см, 6
см.
Задача 20. В правильный треугольник
вписан квадрат так, что две его вершины лежат на одной стороне треугольника, а
две другие вершины – на двух других сторонах треугольника. Найти отношение их
периметров.
Дано:

 DABC ( AB=BC=AC ),
DABC ( AB=BC=AC ),
MNPQ – квадрат, вписан в DABC,
NÎAB, PÎBC, M,QÎAC.

Найти:
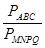
.
Решение:
1) BD – высота DABC.
2) Обозначим
AB=a, MN=x.
3) NPúçAC (по условию) ÞÐBNP=ÐBPN=ÐA=ÐC=60°.
4) П.3
ÞDBNP – равносторонний.
5) BE – высота DBNP.
6) DE=MN=x.
7) Из
DBDC по теореме Пифагора BD=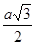 .
.
8) П.7
Þ
BE=BD-ED=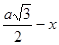 .
.
9) DBNP DBAC (по углам) Þ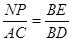 ,
,
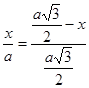 Þ
x=
Þ
x=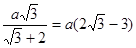
10) 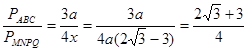 .
.
Ответ: 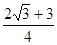 .
.


 Задача 21. Площадь треугольника ABC равна P.
Прямая DE,параллельная
основанию AC, отсекает
от треугольника ABC
треугольник BED
площадью Q. На стороне AC взята произвольная точка M и соединена отрезками
прямых с точками D и E.Чему равна площадь
четырехугольника BEMD?
Задача 21. Площадь треугольника ABC равна P.
Прямая DE,параллельная
основанию AC, отсекает
от треугольника ABC
треугольник BED
площадью Q. На стороне AC взята произвольная точка M и соединена отрезками
прямых с точками D и E.Чему равна площадь
четырехугольника BEMD?
 Дано:
Дано:
DАВС,
SABC=P,
DEúçAC,
SBED=Q,
(×) МÏАС.
Найти:
SBEMD.
Решение:
1)
заметим, что четырехугольник BEMD состоит из фиксированного
треугольника BED и
подвижного, зависящего от выбора точки M, треугольника DEM.
Но где бы на AC мы не
выбрали точку М, высота DDEM,
проведенная к его основанию DE
из точки М, не изменяется по его длине, значит, не изменяется и площадь
треугольника DEM.
Следовательно, точку М мы можем расположить на АС наиболее выгодным для
нас способам, например, совместить ее с точкой А. И тогда речь будет идти об
отыскании площади четырехугольника BEMD, а треугольника BEA с той же площадью.

2) Рассмотрим
DABE
DBDE:
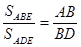 (т.к. у
треугольников общая высота, а, значит, их площади относятся как основания).
(т.к. у
треугольников общая высота, а, значит, их площади относятся как основания).
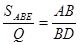 .
.
3)
DABC
DBDE (по углам) Þ
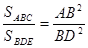 (свойство площадей
подобных фигур)
(свойство площадей
подобных фигур)
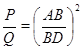 .
.
4) п.2,
п.3 Þ
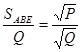 Þ
S
Þ
S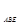 =
=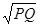 .
.
Ответ: 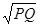 .
.
Задача 22. В прямоугольном
треугольнике биссектриса прямого угла отсекает на гипотенузе длиной a и c. Найдите площадь квадрата, стороной
которого является эта биссектриса.

Решение:
1)
CM – биссектриса
Þ
AC : a = BC : c Þ AC = a×BC/c.
2)


По
теореме Пифагора из DABC:
AB

=AC

+BC

Þ
Þ (a+c)

=(a

/c

)BC

+BC

Þ
Þ B C
C =(a+c)
=(a+c) /(a
/(a /c
/c +1)=
+1)=
=c (a+c)
(a+c) /(a
/(a +c
+c ) Þ
) Þ
Þ BC=c(a+c)/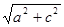 .
.
3) DMHC – прямоугольный, ÐMCH=45°,тогда MC=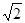 MH.
MH.
4) MHúçBC ÞDAHM и DACM подобны по двум углам Þ
ÞMH
: BC=AM : AB ÞMH : BC = a : (a+c) Þ
Þ MH = a×BC/(a+c).
5) п.2.
4 ÞMH = ac/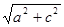 .
.
6) п.3,
5 ÞMC = ac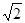 /
/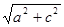 .
.
7) S = MC = 2a
= 2a c
c /(a
/(a +c
+c ).
).
Ответ: 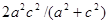 .
.
Задача формирует умения разбивать условие
задачи на данные и требования, находить связи между данной задачей и
теоремами, обобщать, вводить новые неизвестные, контролировать каждый шаг
решения задачи, формулировать ответ.
Задача 23. Отношение величин двух
углов треугольника равно 2, а разность длин противоположных им сторон равна 2
см; длина третьей стороны треугольника равна 5 см. вычислить площадь
треугольника.
Решение:
1)


пусть
ÐА=ÐВ.
проведем биссектрису АК.
2)
Рассмотрим треугольники АВС и АКС.
3)
 ÐАВС=ÐКАС
(т.к. АК – биссектриса).
ÐАВС=ÐКАС
(т.к. АК – биссектриса).
4)

ÐАКС=180°-ÐКАС-ÐВАС
ÐВАС=180°-ÐАВС-ÐВСА
п.3.ÞÐАКС=ÐВАС.
5)
П.3,4Þ треугольники АВС и КАС подобны ( по двум углам)
6)
П.5ÞАС/ВС=СК/АСÞ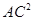 =ВС×СК (*).
=ВС×СК (*).
7)
АК- биссектриса ÞАС/СК=АВ/ВК, АВ=5 смÞ
АС/СК=5/ВК.
8)
ВК=ВС-СК
9)
П.7,8ÞАС/СК=5/(ВС-СК)
5СК=АС×ВС-АС×СК
СК=АС×ВС/(5+АС) (**).
10)
(*),(**)ÞАС =АС×ВС/(АС+5)
=АС×ВС/(АС+5)
АС+5АС=ВС.
11)
ВС=АС+2 (по усл.), п.10,ÞАС +5АС=АС
+5АС=АС +4АС+4
+4АС+4
АС=4см,
ВС=6см.
12)
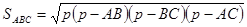 .
.
13)
p=(AB+BC+AC)/2=(5+6+4)/2=7.5
см.
14)
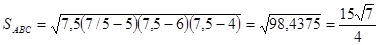 см
см .
.
Ответ: 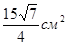 .
.
Данная задача
направлена на формирование умений находить связи между данными и требованиями
задачи, переносить знания в новую ситуацию, сравнивать, контролировать каждый
шаг решения задачи.
Задача 24. Диагонали четырехугольника
равны, а длины его средних линий равны а и с. Найдите площадь четырехугольника.
Решение:
1)






пусть
К, Н, Т, М - соответственно середины
сторон АВ, ВС, СР, АР четырехугольника АВСР.
2)

КН
– средняя линия DАВСÞКН=0,5АС
(по свойству средней линии треугольника).
3)
Аналогично, МТ=0,5АС.
4)
П.2.3ÞКН=МТ=0,5АС.
5)
Аналогично, НТ=КМ=0.5ВР.
6)
АС=ВР (по условию).
7)
П.4,5,6ÞКН=МТ=НТ=КНÞКНТМ – ромб.
8)
КНТМ - ромбÞ НМ^КТ. (по свойству ромба).
9)
НМ^КТÞSKNTM=0,5×НМ×КТ.
10)
НМ=а, КТ=с (по условию).
11)
П.9,10ÞSKHTM=0,5ас.
12)
Обозначим площадь четырехугольника через S.
13)
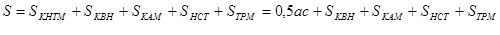
14)
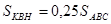 , т.к. площади подобных фигур относятся как квадраты их
линейных размеров (DКВН
и DАВС
подобны по двум углам, т.к. КН- средняя линия DАВС).
, т.к. площади подобных фигур относятся как квадраты их
линейных размеров (DКВН
и DАВС
подобны по двум углам, т.к. КН- средняя линия DАВС).
15)
Аналогично, SМНР=0,25SAPC.
16)
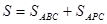
17)
п.14,15,16Þ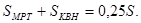
18)
Аналогично, 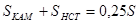 .
.
19)
П 13,18,19Þ S=0,5ac+0,25S+0,25SÞS=ac.
Ответ: ас.
Данная задача
формирует умения разбивать условие задачи на данные и требования, находить
связи между данной задачей и задачей с известным решением, применять аналогию
преобразовывать данные элементы, разбивать задачу на более частные задачи,
переносить знания в новую ситуацию, грамотно оформлять решение задачи, проверять
ход решения задачи
Задача 25. Площадь
треугольника АВС S1;
площадь треугольника АОВ, где О – точка пересечения высот, равна S2. На прямой СО взята точка
К такая, что треугольник АВК – прямоугольный. Докажите, что площадь
треугольника АВК есть среднегеометрический между S1 и S2.
Решение:
1)



Пусть
DАВС-остроугольный,
т.е. т.О лежит внутри DАВС.
2)



DАВК –
прямоугольный, КМ- высотаÞ
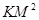
=АМ×МВ (т.к. в прямоугольном треугольнике высота,
опущенная на гипотенузу, равна среднему геометрическому между отрезками, на
которые ее основание делит гипотенузу.
3)
ÐМАН=90°-ÐАВН=ÐВСМ, ÐАМО=ÐСМВ=90°ÞDАОМ и DСВМ подобныÞ АМ:МО=СМ:МВÞАМ×МВ=МО×СМ.
4)
п.2,3ÞКМ =МО×СМ.
=МО×СМ.
5)
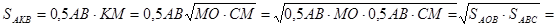
=
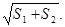
6)


Пусть DАВС – прямоугольный (ÐС=90°),
тогда точки С, О и К совпадают, т.е.
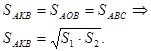
7)








Пусть треугольник АВС – тупоугольный,
тогда точки О и К лежат вне DАВС. Проведем рассуждения аналогичные доказательству,
проведенному для остроугольного треугольника. Получим:
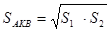
.
Данная задача
направлена на формирование умений делать схематическую запись условия задачи,
разбивать условие задачи на данные и требования, находить связи между данными и
требованиями задачи, находить связи между задачей и теоремами, разбивать задачу
на более частые задачи, проверять ход решения задачи, грамотно оформлять
решение задачи, исследовать задачу.
Предложенные
задачи взяты из различных сборников. Хороший, но не легкий путь составить
задачу самому. Полезно подбирать вопросы проблемного характера и к стандартным
задачам.
Самую обычную
задачу можно сделать творческой, если создать в классе атмосферу поиска,
размышления, когда ученики начинают искать и находят несколько способов решения
одной и той же задачи; подать эту задачу так, чтобы каждый этап ее решения
заставлял их обдумывать свои действия.
Нелегко
требовать переделки всех задач в проблемные. Стандартные задачи, позволяющие
закрепить навык, формулу, алгоритм необходимы. Но важно избегать единообразия,
чаще предлагать ребятам задачи проблемные.
Говоря о
значении проблемных задач, хочется отметить, что только такие задачи ведут к
приобретению учащимися по-настоящему глубоких знаний.
Заключение.
Рассматривая
проблемное обучение как фактор интеллектуального развития школьников, мы
изучили и проанализировали психолого-педагогическую и методическую литературу
по интересующим нас вопросам. В нашей работе мы опирались на труды Ю.К.Бабанского,
П.Я.Гальперина, Н.А.Менчинской, А.М.Матюшкина, М.И.Махмутова и других авторов.
Исходя из
анализа литературы, мы раскрыли сущность проблемного обучения и
интеллектуального развития. Мы рассмотрели возможность интеллектуального
развития в условиях проблемного обучения, его организацию и руководство в
процессе обучения. Раскрывая эти вопросы, мы пришли к выводу, что проблемное
обучение – фактор интеллектуального развития школьников.
Нами была
разработана система уроков с элементами проблемного обучения и составлена
подборка проблемных заданий. Каждый урок
не только на изучение теоретического материала и формирование умений
решать задачи, но и на организацию умственной деятельности учащихся, которая способствует
интеллектуальному развитию.
Кроме
обучающей серии, наш эксперимент состоял из констатирующей и контрольной серий.
Для их проведения были отобраны методики исследования интеллектуальных умений,
определяющие уровень интеллектуального развития.
Разработанные
уроки и опытная работа были проведены в средней школе № 67 Советского района
города Самары. Результаты проведенного исследования показали эффективность
разработанной системы уроков и составленной подборки задач.
Проблема
организации интеллектуального развития школьников на уроках с элементами
проблемного обучения меня очень заинтересовала, и в будущей своей
педагогической деятельности планирую и дальше ей заниматься.
Библиография.
1.
Анастази А. Психологическое тестирование.
Ч.1-2.-М.,1982.
2.
Бабанский Ю.К. Интенсификация процесса
обучения.-М.:Знание, 1987.
3.
Бабанский Ю.К. Методы обучения в современной
общеобразовательной школе.-М.:Просвещение, 1985.
4.
Бабанский Ю.К. Оптимизация учебно-воспитательного
процесса.-М.:Просвещение, 1982.
5.
Бабанский Ю.К. Проблемное обучение как средство
повышение эффективности учения школьников.-Ростов-на-Дону, 1970.
6.
Бабанский Ю.К. Рациональная организация учебной
деятельности.-М., 1981.
7.
Блейхер В.М., Бурлачук Л.Ф. Психологическая диагностика
интеллекта и личности.-Киев.: «Вища школа», 1978.
8.
Богданова Т.Г., Корнилова Т.В. Диагностика
познавательной сферы ребенка.-М.:Роспедагентство, 1994.
9.
Богоявленский Д.Н., Менчинская Н.А. Психология усвоения
знаний в школе.-М.,1959.
10. Величковский
Б.М. Как устроен естественный интеллект.//Природа.- 1988.-№ 12.
11. ВилькеевД.В.
Познавательная деятельность учащихся при проблемном характере обучения основам
наук в школе.-Казань, 1967.
12. Воспитание
ученика. Сборник программно-методических материалов. Сост.В.М.Коротов,
Н.А.Лошкарева, В.Н.Зайцев..-М., 1990.
13. Гальперин
П.Я. Методы обучения и умственное развитие ребенка.-М.:Изд-во МГУ, 1985.
14. Гузик
Н.П. Учить учиться.-М.: Педагогика, 1981.
15. Доровской
А.И. Сто советов по развитию одаренности детей. Родителям, воспитателям,
учителям.-М., Роспедагентство, 1997.
16. Коротяев
Б.И. Учение – процесс творческий : Кн. для учителя: Из опыта
работы.-М.:Просвещение, 1989.
17. Краткий
словарь по философии /Под ред. И.В.Блауберга, И.К.Пантина.-М.:Политиздат,1982.
18. Крутецкий
В.А. Основы педагогической психологии.-М.:Просвещение, 1972.
19. Крутецкий
В.А. Психология математических способностей школьников.-М.:Просвещение, 1968.
20. Крутецкий
В.А. Психология обучения и воспитания школьников.-М., 1976.
21. Кудрявцев
Т.В. Исследование и опыт проблемного обучения. В кн.: «О проблемном обучении»:
Вып. 2.-М.:Высшая школа, 1969.
22. Кудрявцев
Т.В. Проблемное обучение: истоки, сущность, перспективы.-М.:Знание, 1991.
23. Кулько
В.А., Цехмистрова Т.Д. Формирование у учащихся умений учиться: Пособие для
учителей.-М.:Просвещение, 1983.
24. Лернер
И.Я. Вопросы проблемного обучения на Всесоюзных педагогических
чтениях.//Советская педагогика.- 1968.-№ 7.
25. Лернер
И.Я. Система методов обучения.-М.:Знание, 1976.
26. Людмилов
Д.С.,Дышинский Е.А.,Лурье А.М. Некоторые вопросы проблемного обучения
математике: Пособие для учителей.-Пермь, 1975.
27. Лоповок
Л.М. Тысяча проблемных задач по математике: Кн. для учащихся.-М.:Просвещение,
1995.
28. Матюшкин
А.М. Проблемные ситуации в мышлении и обучении.-М.:Педагогика, 1972.
29. Махмутов
М.И. Организация проблемного обучения в школе. Книга для
учителей.-М.:Просвещение, 1977.
30. Махмутов
М.И. Проблемное обучение. Основные вопросы теории.-М.:Педагогика, 1975.
31. Мелхорн
Г, Мелхорн Х.-Г. Гениями не рождаются: общество и способности человека: Кн. для
учителя.-М.:Просвещение, 1989.
32. Менчинская
Н.А. Проблемы учения и умственного развития школьника.-М, 1989.
33. Мочалова
Н.М. Методы проблемного обучения и границы их применения.-Казань, 1978.
34. Обухова
Л.Ф. Этапы развития детского мышления.-М.,1972.
35. Оконь
В. Введение в общую дидактику.-М.:Высш.шк., 1990.
36. Оконь
В. Основы проблемного обучения.-М.:Просвещение, 1968.
37. Паламарчук
В.Ф. Школа учит мыслить.-М.:Просвещение, 1987.
38. Педагогическая
энциклопедия/ Под ред. И.Я.Каирова, Ф.Н.Петрова, Т. 3.-М.: «Советская
энциклопедия», 1966.
39. Педагогический
словарь/ Под ред. Г.М.Воловниковой, Л.И.Генсиоровской, Т. 2.-М.: Изд-во АПН
РСФСР, 1959.
40. Погорелов
А.В. Элементарная геометрия.-М., 1977.
41. Поиски
рациональных способов преподавания математики (из опыта учителей
Татарии).-М.:Просвещение, 1968.
42. Развитие
учащихся в процессе обучения: Под ред. Л.В.Занкова.-М., 1963.
43. Рубинштейн
С.Л. О мышлении и путях его исследования.-М., Изд-во АН СССР, 1958.
44. Рубинштейн
С.Л. Основы общей психологии.-М., 1989.
45. Супрун
В.П. Избранные задачи повышенной сложности по математике:-Мн:Полымя, 1998.
46. Талызина
Н.Ф., Карпов Ю.В. Педагогическая психология: Психодиагностика интеллекта.-М.:
Изд-во МГУ,1987.
47. Талызина
Н.Ф. Формирование познавательной деятельности учащихся.-М.:Знание, 1983.
48. Формирование
умений и навыков учебного труда в процессе обучения школьников. Сборник научных
трудов. Под ред. В.В.Краевского, А.В.Усовой.-М., 1981.
49. Фридман
Л.М. Психологические основы обучения математике в школе: Учителю математики о
педагогической психологии.-М.:Просвещение, 1983.
50. Шамова
Н.В. Активизация учения школьников.-М.:Просвещение, 1982.
51. Юркевич
В.С. Одаренный ребенок: иллюзии и реальность: Кн. для учителей и
родителей.-М.:Просвещение, 1996.