Полагающиеся аннуитеты

Аннуитет является последовательностью периодических платежей, обычно одинаковых, сделанных через одинаковые промежутки времени. Наиболее известными примерами аннуитетов являются платежи премий страхования жизни, платежи рассрочки, платежи ренты и т.д.

Период времени между двумя последовательными платежами называется интервалом платежа и может быть любой удобной продолжительности. Первоначально слово аннуитет относилось только к ежегодным платежам, но современное использование этого термина может предусматривать интервалы платежа любой продолжительности.

Сроком аннуитета является время от начала первого интервала платежа до окончания последнего интервала платежа. Когда срок аннуитета фиксирован, то есть когда срок начинается и заканчивается в определенные даты, аннуитет называется определенным (детерминированным) аннуитетом. Когда срок аннуитета зависит от некоторого неопределенного события, такого как смерть человека, аннуитет называется зависимым (случайным) аннуитетом.

Когда платежи производятся в моменты окончания интервалов платежа, аннуитет называется обыкновенным аннуитетом. Когда платежи производятся в начальные моменты интервалов платежа, аннуитет называется полагающимся аннуитетом. В дальнейшем, следуя принятой на практике традиции, слово аннуитет будет означать обыкновенный аннуитет, если не оговорено другое.

Предположим, что Иванов покупает автомобиль в рассрочку, выплачивая наличными 3 млн рб в день покупки и затем ежемесячно 1 млн рб в течение 24 месяцев, первый взнос по истечению 1 месяца после даты продажи. Ежемесячные взносы составляют обыкновенный аннуитет, срок которого начинается в день продажи и продолжается в течение двух лет. Интервал платежа равен 1 месяцу.

Все задачи об аннуитетах касаются полной стоимости серии платежей на некоторую заданную дату. Можно было бы рассмотреть все эти задачи методами, развитыми в предшествующих разделах. Однако, используя свойство регулярности платежей аннуитетов, вычисление полной стоимости может быть существенно упрощено.

Иногда желательно считать, что срок аннуитета начинается датой первого платежа. В этом случае периодические платежи производятся в начальные моменты интервалов платежа, а не в конце. Такой аннуитет называется полагающимся аннуитетом и состоит из серии периодических платежей, производимых в начальные моменты интервалов платежей, со сроком, начинающимся датой первого платежа и заканчивающимся через один интервал после последнего платежа.

Так как настоящая стоимость аннуитета была определена как эквивалентная сумма на начало срока, значит настоящая стоимость полагающегося аннуитета является эквивалентной суммой на момент первого платежа. В свою очередь, итоговая сумма аннуитета была определена как эквивалентная сумма на конец срока, поэтому итоговая сумма полагающегося аннуитета является эквивалентной суммой на дату окончания интервала платежа, который начался в момент последнего платежа.

A будет обозначать настоящую стоимость, S – итоговую сумму, R - стоимость периодического платежа и i - норму процента за интервал платежа полагающегося аннуитета из n платежей.

Определение A. Способ 1. Выписывается уравнение эквивалентности с датой сравнения, установленной на интервал платежа раньше даты первого платежа. На эту дату n платежей R могут рассматриваться как обыкновенный аннуитет. Следовательно,

A(1 + i) -1 = R a n i .

Из этого равенства получаем

A = (1 + i) R a n i .

Способ 2. Выписывается уравнение эквивалентности с датой сравнения, установленной на дату начала срока. Платеж в этот день рассматривается как выплата наличными, а остальные n-1 платежей могут рассматриваться как обыкновенный аннуитет. Поэтому

A = R + R an i _ 1 = R(1 + an i _ 1 ).

Определение S. Способ 1. Выписывается уравнение эквивалентности с датой сравнения, установленной на дату последнего платежа. На эту дату платежи могут рассматриваться как обыкновенный аннуитет.

Следовательно,

S(1 + i) -1 = R s n i .

Разрешая это соотношение относительно S , получим

S = (1 + i) R s n i .

Способ 2. Обращаясь снова к временной диаграмме, можно увидеть, что если добавить дополнительный платеж в конце последнего интервала платежа, получающаяся серия платежей (начинающаяся за интервал платежа до начала срока рассматриваемого аннуитета) может рассматриваться как обыкновенный аннуитет с n + 1 платежами. Этот дополнительный платеж увеличивает сумму S ровно на R , так как делается в день окончания срока аннуитета. Поэтому

S + R = R sn_ 1i .

Отсюда итоговая сумма полагающегося аннуитета равна

S = R sn_ 1i - R = R( sn_ 1i - 1) .

Знакомясь со способами расчета A и S , следует иметь ввиду, что главное здесь не полученные формулы, а рассуждения, с помощью которых они получены. Именно такого рода рассуждения часто используются при решении разнообразных финансовых проблем, как можно увидеть позже.

Пример 1 Найти эквивалентную стоимость холодильника, который может быть куплен в течение полутора лет ежемесячными платежами по 200000 руб., если деньги стоят j12 = 6% .

Решение

Способ 1. На дату, помеченную -1 , платежи образуют обыкновенный аннуитет из 18 платежей, а эквивалентная сумма A рассчитывается на 1 интервал платежа позже. Уравнение эквивалентности на дату сравнения -1 имеет вид

A(1,005) -1 = 200000 × a 1 8 0 , 0 0 5

поэтому

A = 201000 × 17,172768 = 3451726 рб.

Способ 2. Первый платеж можно рассматривать как выплату наличными, а остальные 17 платежей считать обыкновенным аннуитетом со сроком, начинающимся в день покупки. Тогда из уравнения эквивалентности с датой сравнения в день покупки получим

A = 200000 + 200000 × a 1 7 0 , 0 0 5 = 200000 × (1 + 16,258632) = 3451726 рб.

Пример 2 Сберегательный банк начисляет проценты с нормой j2 = 4%

Если на депозитный счет вносить в начале каждого полугодия по 50000 рб, какая сумма будет лежать на этом счете через 12 лет ?

Решение

Способ 1. Выпишем уравнение эквивалентности, используя дату последнего платежа как дату сравнения. На эту дату накопленная сумма платежей равна итоговой сумме обыкновенного аннуитета, поэтому

S(1,02) -1 = 50000 × s 2 4 0 , 0 2 .

Отсюда имеем

S = 51000 × 30,421862 = 1551515 рб.

Способ 2. В конце 24-го интервала платежа добавим лишние 50000 рб к серии платежей аннуитета и добавим также 500000 рб к эквивалентной сумме S. Уравнение эквивалентности на конец 24-го интервала теперь  примет вид

S + 50000 = 50000 × s 2 5 0 , 0 2 .

Из него находим

S = 50000( s 2 5 0 , 0 2 - 1 ) = 50000(32,0303 - 1) = 1551515.

Задачи

1. инвестор ссудил 40млн.руб и получил вексель с обязательством заплатить эту сумму плюс 6 процентов через 9 дней. Вексель был немедленно продан банку, который начисляет 5 процентов банковского дисконта. Какова прибыль инвестора? Какую норму процента реализует банк при окончании векселя?

Решение:

Таким образом, инвестор получит следующую прибыль:

40 млн. руб. * (6% + 5%) = 4,4 млн. руб.

При окончании векселя банк получит прибыль в размере:

40 млн. руб. * 5% = 2 млн. руб.

2. сколько дней понадобится, чтобы 7000 руб. заработали 100 руб., если они инвестируются при 8% обыкновенного простого процента?

Решение:

Для расчета воспользуемся формулой простых процентов:

S = P*(1 + i*t/k),

Где: S -  наращенная сумма,

i – ставка процентов,

t – количество дней обращения средств,

k – количество дней в году.

Нам необходимо определить t.

Подставляя данные в исходную формулу получим:

7100 = 7000*(1 + 0,08*t/365)

7100/7000 = 1 + 0,08*t/365

1,014 – 1 = 0,08*t/365

t = 0,14*365/0,08 = 638,75 дней.

3. Найти датированную сумму по окончании двух лет, при j2 = 5%, эквивалентную 5млн.руб. с процентами за 8 лет при j2 = 4%.

Решение:

Найдем первоначальную сумму вложений при сроке вложения 8 лет:

5 = Р*(1 + 0,04/2)^2*8

5 = Р*1,372

Р = 3,642

Далее найдем датированную сумму по окончании 2 лет:

S = 3,642*(1 + 0,05/2)^2*2

S = 4,020 млн. руб.

4. Найти эффектную ставку, при которой 10млн.руб теперь эквивалентны 20млн.руб через 14 лет.

Решение:

Обозначим эффективную ставку через i. По определению множители наращения по двум ставкам (эффективной и номиналь­ной при m-разовом начислении) должны быть равны друг другу:

#

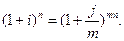10*(1 + i) = 20*(1 + i)²⁰

10 = 20*(1 + i)¹⁹

20*19ln(1 + i) = ln 10

1 + i = e^0,006

i = e^0,006 – 1

i = 1,006 – 1 = 0,006 или 0,6%

5. при какой номинальной ставки j2 деньги удваиваются через 20 лет?

Решение:

Формулу на­ращения теперь можно представить следующим образом:

#

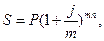Где: j – ставка процентов,

m – количество начислений в год.

2 = 1*(1 + j/2)^2*20

ln2 = ln(1 + j/2)^2*20

40ln(1 + j/2) = ln2

ln(1 + j/2) = 0,693/40

ln(1 + j/2) = 0,017

1 + j/2 = e^0,017

j = (e^0,017 – 1)*2

j = 0,034 или 3,4%

Список литературы

1.     Кочович Е. Финансовая математика. М.: «Финансы и статистика». 1994г.

2.     Кутуков В.Б. Основы финансовой и страховой математики. М.: ДЕЛО. 1998г.

3.     Мелкумов Я.С. Теоретическое и практическое пособие по финансовым вычислениям. М.: ИНФРА-М. 1996г.

4.     Овчаренко Е.К., Ильина О.П., Балыбердин Е.В. Финансово-экономические расчеты в Excel. Изд 2-е, доп. – М.: Информационно-издательский дом "Филинъ", 1998.-184 с.

5.     Четыркин Е.М. Финансовая математика. –М.: Дело, 2000.